Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get a quasirandom point based on Kronecker sequences
ResourceFunction["KroneckerPoint"][n] return | |
ResourceFunction["KroneckerPoint"][dim,n] return |
Generate the first point:
| In[1]:= |
| Out[1]= |
Numeric approximation of the first three points:
| In[2]:= |
| Out[2]= |
The first three points with ρ (rho) as the plastic constant:
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= | 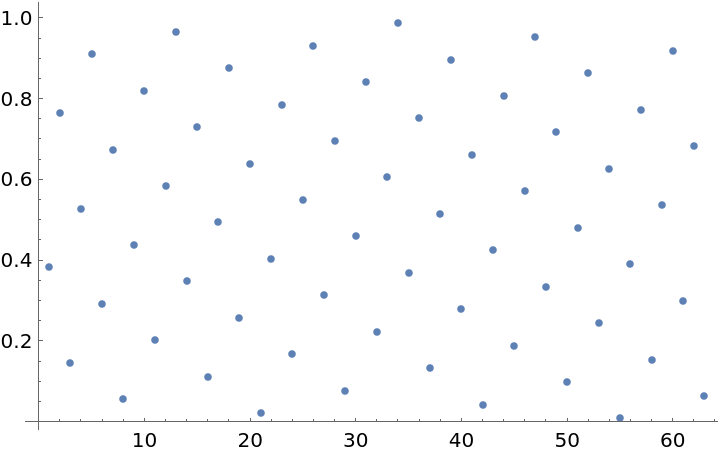 |
Show the structure of the plastic quasirandom sequence:
| In[5]:= |
| Out[5]= |  |
The first 500 points as Voronoi cells:
| In[6]:= |
| Out[6]= |  |
Show the dimension 3 points:
| In[7]:= |
| Out[7]= | 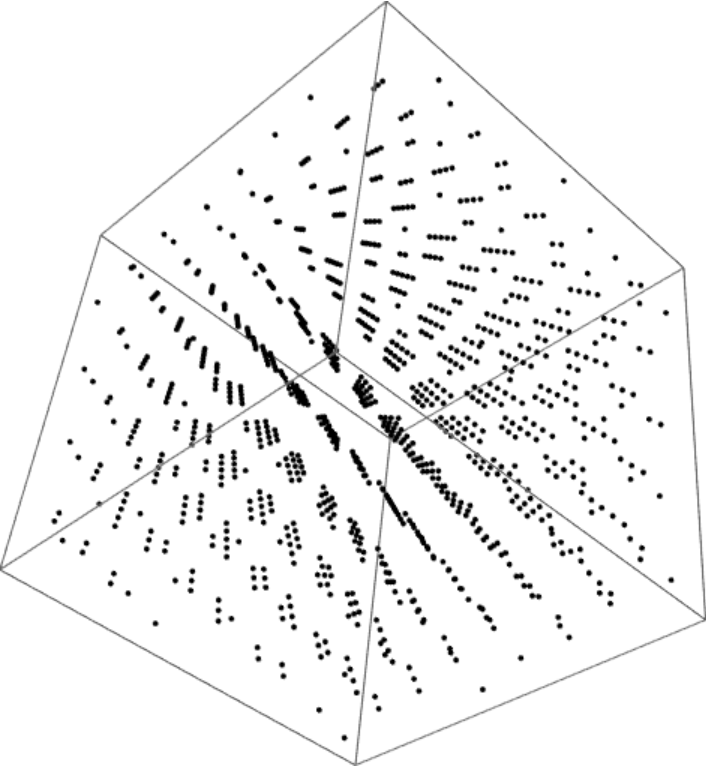 |
The plastic sequence can be folded into a triangle and still be a low-discrepancy sequence:
| In[8]:= | ![Manipulate[
Graphics[
Point /@ (If[fold && Total[#] > 1, 1 - #, #] & /@ ResourceFunction["KroneckerPoint"][Range[k]])], {{k, 400, "points"}, 10, 2000, 1, Appearance -> "Labeled"}, {{fold, True}, {True, False}}, SaveDefinitions -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/57f/57fe35a9-cd2a-4108-8781-ab5a79d88c84/54699a2212788192.png) |
| Out[8]= | 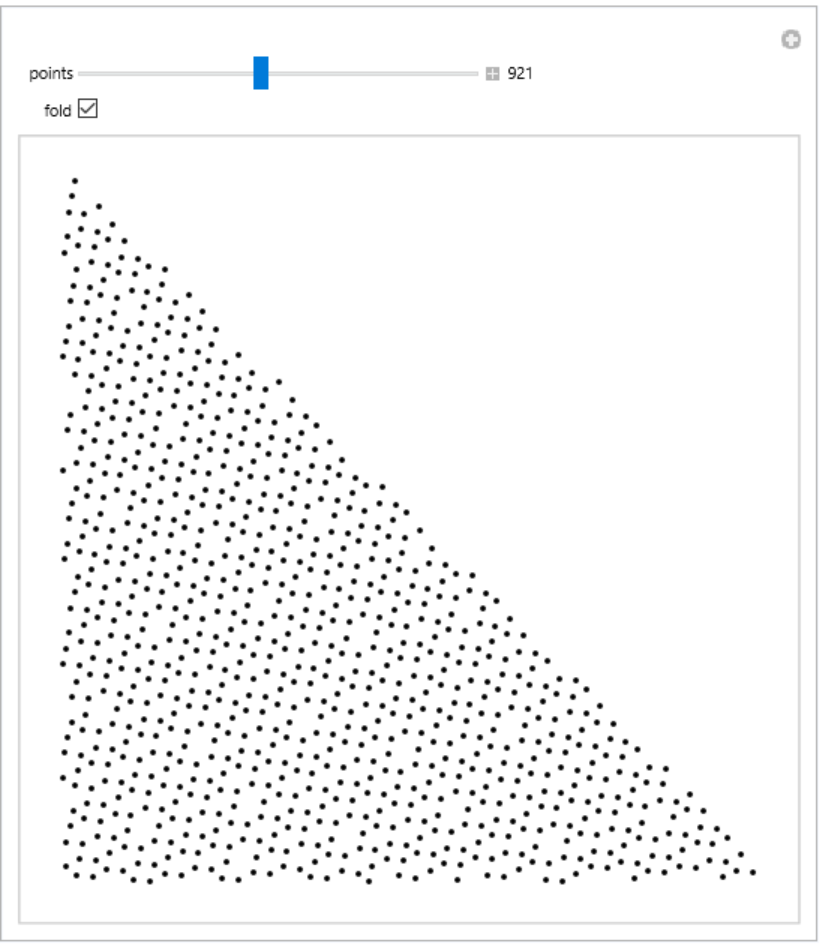 |
This work is licensed under a Creative Commons Attribution 4.0 International License