Basic Examples (2)
Find the isogonal conjugate of a point with respect to a triangle:
Find the isogonal conjugate of a point with respect to a triangle:
The isogonal conjugate of the isogonal conjugate is the original point:
Show the triangle, point (green) and isogonal conjugate (blue):
The centers of the incircle and excircles are the only four self-conjugate points:
The product of trilinear coordinates for a point and isogonal conjugate gives three identical values:
Scope (3)
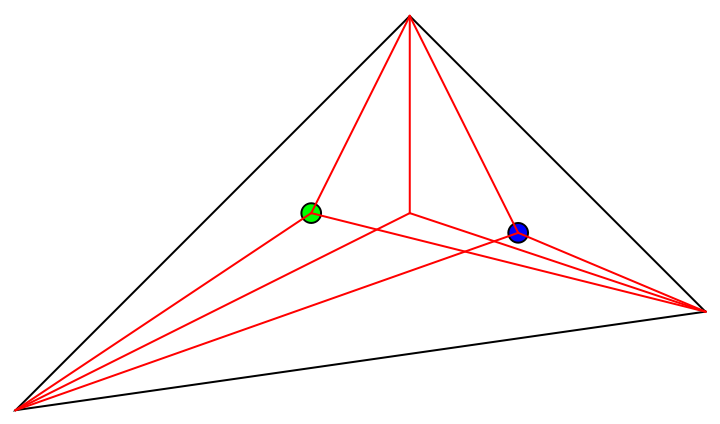
Find the Monge point of a semi-random tetrahedron:
Find the isogonal conjugate of the Monge point:
The circumsphere of the face reflections of a point is centered at the isogonal conjugate (and vice-versa):
Neat Examples (2)
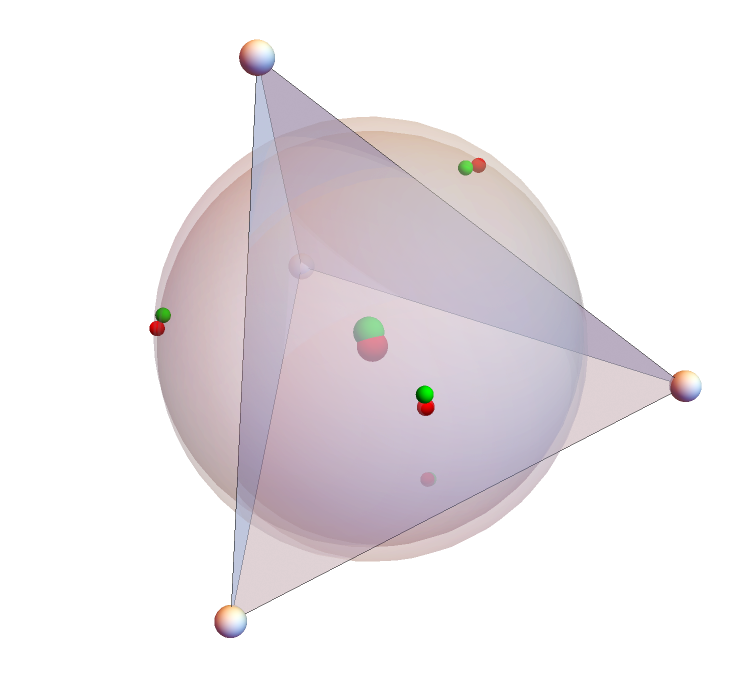
For a tetrahedron, calculate the five insphere and exsphere points:
These five points are all equal to their isogonal conjugates:
Three other points are their own isogonal conjugate in a tetrahedron:
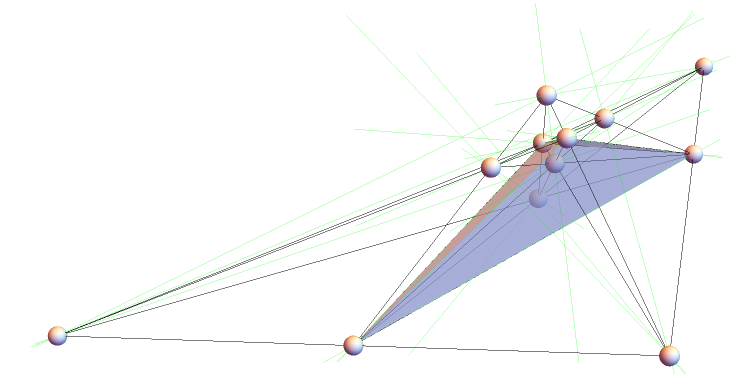
Show the 16 collinear sets of three points formed by four tetrahedral points and eight self-conjugates:
Find intersection points and repeat to obtain 50 lines:
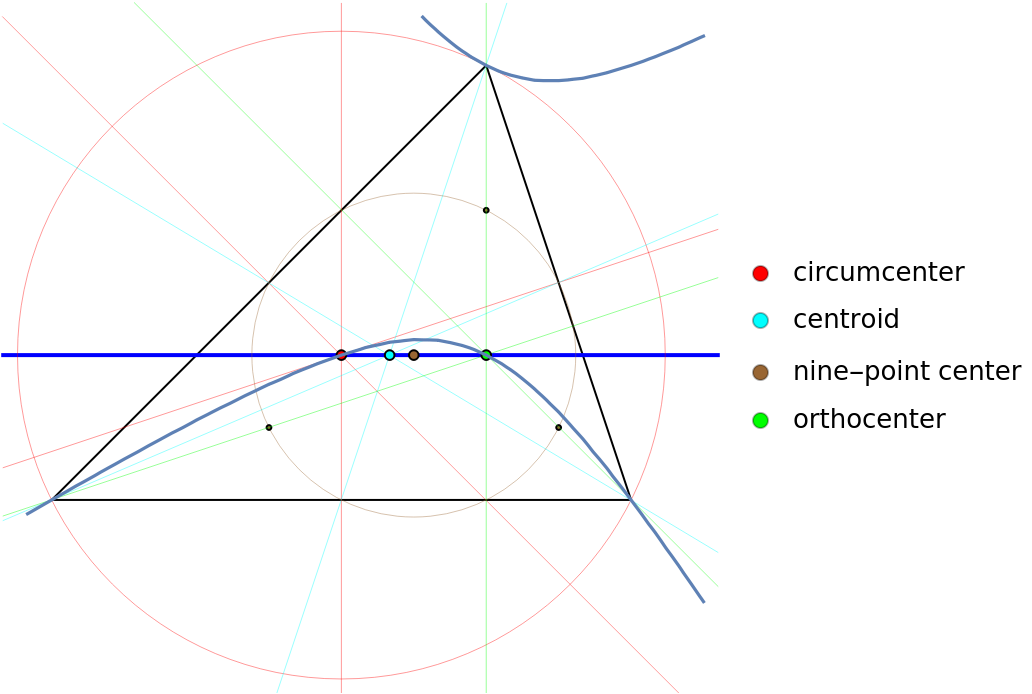
The following triangle has nice Euler line points for the circumcenter, centroid, nine-point center and orthocenter:
The Jerabek hyperbola is the locus of the isogonal conjugates of points on the Euler line. Use GroebnerBasis to derive the implicit equation:
The isogonal conjugates of the Euler points are the orthocenter, symmedian, Kosnita point and circumcenter:
A graphic of the triangle with the Euler line (blue), circumcenter|circumcircle|perpendicular bisectors (red), centroid|medians (cyan), nine-point center|circle (brown) and orthocenter|altitudes (green) and the isogonal conjugate of the Euler line, the Jerabek hyperbola:
![tri = {{7, 2}, {4, 5}, {0, 1}};
p = {3, 3};
i = ResourceFunction["IsogonalConjugate"][tri, p]](https://www.wolframcloud.com/obj/resourcesystem/images/7f2/7f283ffe-0eab-401d-8d86-aadef0faeb0f/1-0-0/1cd457181d07e30e.png)
![baryP = ResourceFunction["BarycentricCoordinates"][tri, p];
baryI = ResourceFunction["BarycentricCoordinates"][tri, i];
sides = Reverse[EuclideanDistance @@ # & /@ Subsets[tri, {2}]];
trilinearP = (baryP/sides);
trilinearI = (baryI/sides);
trilinearP trilinearI](https://www.wolframcloud.com/obj/resourcesystem/images/7f2/7f283ffe-0eab-401d-8d86-aadef0faeb0f/1-0-0/01e090e60424eb30.png)
![randomtetra = Select[ResourceFunction["SignedPermutations"][12 {1, 1, 1}], EvenQ[Count[Sign[#], -1]] &] + RandomSample[Tuples[{1, 0, -1}, {3}], 4];
mongefull = ResourceFunction["Monge"][randomtetra];
monge = First[mongefull]](https://www.wolframcloud.com/obj/resourcesystem/images/7f2/7f283ffe-0eab-401d-8d86-aadef0faeb0f/1-0-0/0e57aa5935feba77.png)
![reflectM = Flatten[ResourceFunction["ReflectPoints"][#, {monge}] & /@ Subsets[randomtetra, {3}], 1];
reflectI = Flatten[ResourceFunction["ReflectPoints"][#, {isog}] & /@ Subsets[randomtetra, {3}], 1];
Graphics3D[{Sphere[#, 1] & /@ randomtetra,
{Red, Sphere[monge, 1], Sphere[#, 1/2] & /@ reflectM}, {Green, Sphere[isog, 1], Sphere[#, 1/2] & /@ reflectI},
Opacity[.5], Tetrahedron[randomtetra], Opacity[.2],
Circumsphere[reflectM], Circumsphere[reflectI]}, Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/7f2/7f283ffe-0eab-401d-8d86-aadef0faeb0f/1-0-0/2b04882aa53fc820.png)
![pp = Join[tetra, five, same];
lines = ResourceFunction["FindExtraordinaryLines"][pp];
ordinary = Complement[Subsets[Range[12], {2}], Flatten[Subsets[#, {2}] & /@ lines, 1]];
Graphics3D[{Sphere[#, 40] & /@ pp, Line[pp[[#]]] & /@ lines, Opacity[.5], Tetrahedron[tetra], Green, InfiniteLine[pp[[#]]] & /@ ordinary}, Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/7f2/7f283ffe-0eab-401d-8d86-aadef0faeb0f/1-0-0/3783798da69096fb.png)
![other = Complement[First /@ Select[RegionIntersection /@
Subsets[
Join[InfiniteLine[pp[[#]]] & /@ ordinary, InfiniteLine[pp[[#]]] & /@ lines], {2}], Head[#] === Point &], pp]; qq = Join[pp, other];
lines2 = ResourceFunction["FindExtraordinaryLines"][qq];
Graphics3D[{Sphere[#, 40] & /@ qq, Line[qq[[#]]] & /@ lines2, Opacity[.5], Tetrahedron[tetra]}, Boxed -> False, SphericalRegion -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/7f2/7f283ffe-0eab-401d-8d86-aadef0faeb0f/1-0-0/683c2464cadfc8b4.png)

![mids = Mean /@ Subsets[Reverse[tri], {2}];
otherthree = Mean[{#, euler[[4]]}] & /@ tri;
Legended[
Graphics[{EdgeForm[Black], White, Thick, Triangle[tri], Blue, InfiniteLine[Take[euler, 2]], Thin, Red, InfiniteLine[{euler[[1]], #}] & /@ mids, Circumsphere[tri], Disk[euler[[1]], 0.2], Cyan, InfiniteLine /@ Transpose[{tri, mids}], Disk[euler[[2]], 0.2], Brown, Circle[euler[[3]], EuclideanDistance[euler[[3]], mids[[1]]]], Disk[#, 0.1] & /@ otherthree, Disk[euler[[3]], 0.2], Green, InfiniteLine[{euler[[4]], #}] & /@ tri, Disk[euler[[4]], 0.2],
ContourPlot[
jerabek == 0 // Evaluate, {\[FormalX], -15, 13}, {\[FormalY], -14, 14}][[1]]}], PointLegend[{Red, Cyan, Brown, Green}, {"circumcenter", "centroid", "nine-point center", "orthocenter"}, LegendMarkers -> ConstantArray[Graphics[Disk[]], 3]]]](https://www.wolframcloud.com/obj/resourcesystem/images/7f2/7f283ffe-0eab-401d-8d86-aadef0faeb0f/1-0-0/1c5fd0590f6e6366.png)