Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 IsingModelCA

Source Notebook

Simulate the Ising model using a cellular automaton

Contributed by: Stephen Wolfram

ResourceFunction["IsingModelCA"][n,percent,k]

gives the kth step in the evolution of an n×n Ising model with a percentage percent of black cells.

ResourceFunction["IsingModelCA"][n,percent,k,j]

gives the jth slice of the evolution.

Details

The Ising model is an idealization of ferromagnetic materials involving an n×n array of spins, where each pair of adjacent spins contributes -1 or +1 to the total energy, depending on whether they are parallel or anti-parallel. When the temperature decreases past a critical value, a phase transition occurs between the disordered state and one in which spins tend to align spontaneously, producing magnetization even in the absence of an external field. Technically, in the two-dimensional Ising model, a phase transition only occurs in the limit n→∞.
In physical terms, the value of percent defines the effective temperature (relative to the spin-coupling interaction strength) of the model.

Examples

Basic Examples (3) 

Evolution with 50% of black cells:

In[1]:=
ArrayPlot[ResourceFunction["IsingModelCA"][40, 50, 100]]
Out[1]=

Configurations generated after 50 steps from various initial densities:

In[2]:=
GraphicsGrid[ Partition[ Table[Labeled[ ArrayPlot[ResourceFunction["IsingModelCA"][40, p, 50], ImageSize -> {100, 110}], IntegerString[p] <> "% black"], {p, {5, 10, 15, 20, 25, 30, 40, 50, 60, 70, 75, 80, 85, 90, 95}}], 5], ImageSize -> {650, 410}]
Out[2]=

Slices through their evolution:

In[3]:=
GraphicsRow[ Table[Labeled[ ArrayPlot[ResourceFunction["IsingModelCA"][100, p, 200, 2], ImageSize -> {100, 210}], IntegerString[p] <> "% black"], {p, {8, 10, 12, 13, 15}}], 0, AspectRatio -> 0.45, ImageSize -> 650]
Out[3]=

Requirements

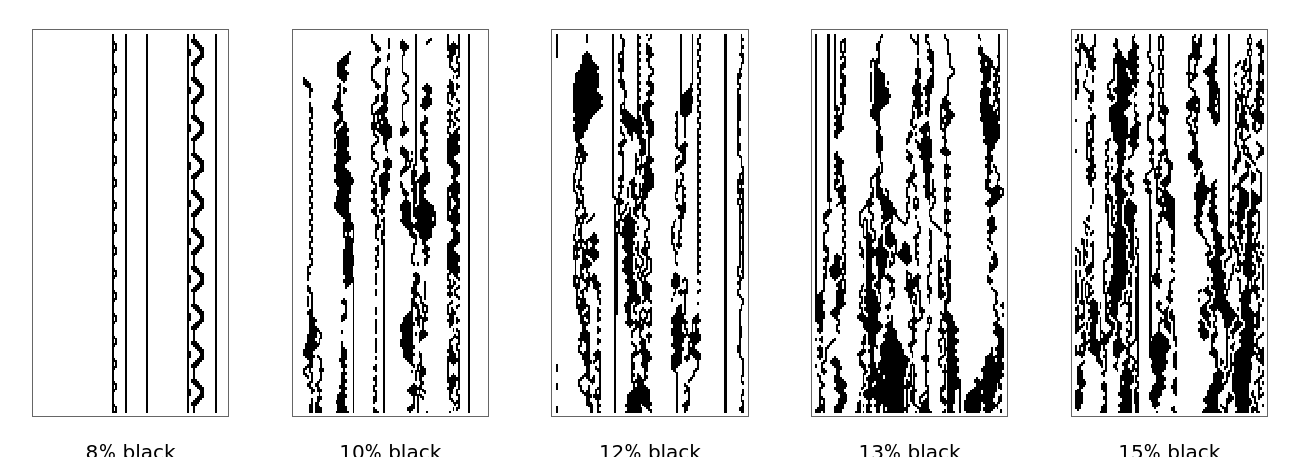Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.1 – 16 August 2021
  • 1.0.0 – 26 April 2019

Source Metadata

  • Citation:
    • Stephen Wolfram (2002), A New Kind of Science

Related Resources

License Information