Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 Intrinsic3DCurve

Source Notebook

Plot intrinsic curves in 3D

Contributed by: Enrique Zeleny

ResourceFunction["Intrinsic3DCurve"][κ,τ,a,b,w,ds,n]

plot an intrinsic curve with curvature κ and torsion τ with parameters a and b and width w in discrete steps ds applied n times.

Details and Options

The French mathematicians Joseph Alfred Serret and Jean Frédéric Frenet found a way to represent a parametrized curve by intrinsic equations.
At each point of the curve (parametrized by arc length), three mutually perpendicular unit vectors are defined (called a TNB frame). The tangent shows the direction of motion of the point, the normal points toward the direction in which the curve bends and the binormal is a vector perpendicular to both.
Another two quantities are introduced: curvature to measure how quickly the curve is changing its direction and torsion to measure how quickly the curve is leaving the TN plane.
The starting point is {0,0,0}.
Options are the same as Graphics3D.

Examples

Basic Examples (4) 

A simple curve:

In[1]:=
ResourceFunction[ "Intrinsic3DCurve"][Sin, Cos, 5.5, 2.18, 0.015, 0.01, 2200]
Out[1]=

Increasing width, we get a ribbon-like surface (in fact, a ruled surface—the other edge has a displaced TNB frame):

In[2]:=
ResourceFunction[ "Intrinsic3DCurve"][Sin, Cos, 5.5, 2.18, 0.19, 0.01, 2200]
Out[2]=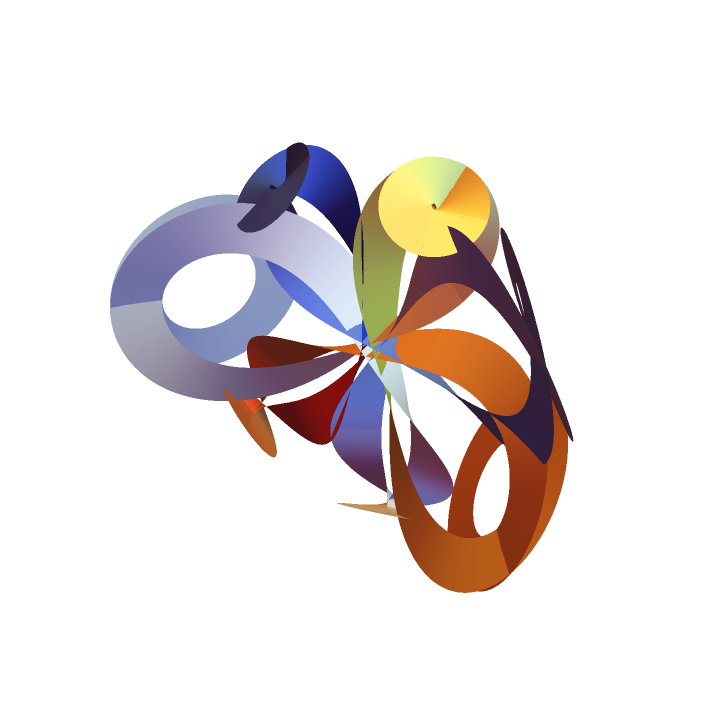

With a constant function:

In[3]:=
ResourceFunction["Intrinsic3DCurve"][ 1 &, Sin, 1., 1., 0.3, 0.01, 1255]
Out[3]=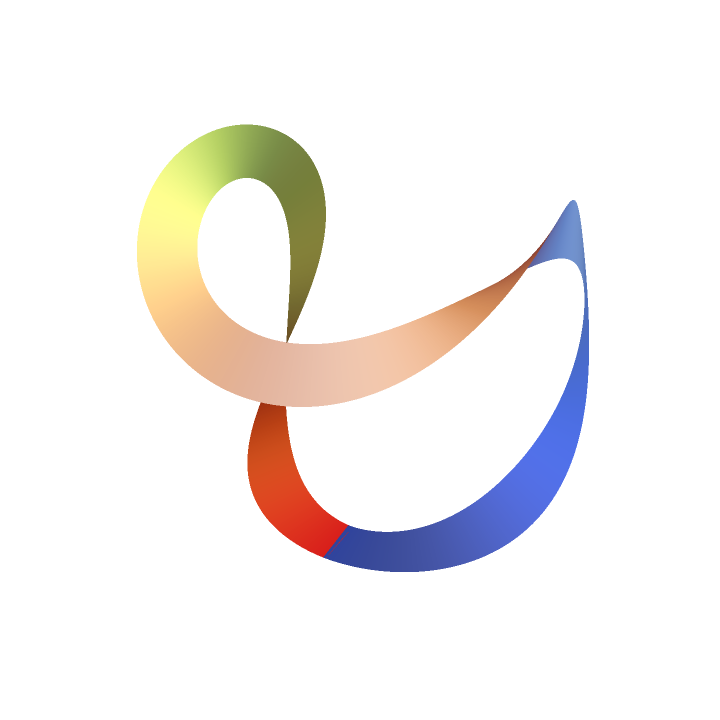

A higher constant function:

In[4]:=
ResourceFunction["Intrinsic3DCurve"][Sin, 3 &, 2.25, .5, 1., 0.073, 560]
Out[4]=

Possible Issues (2) 

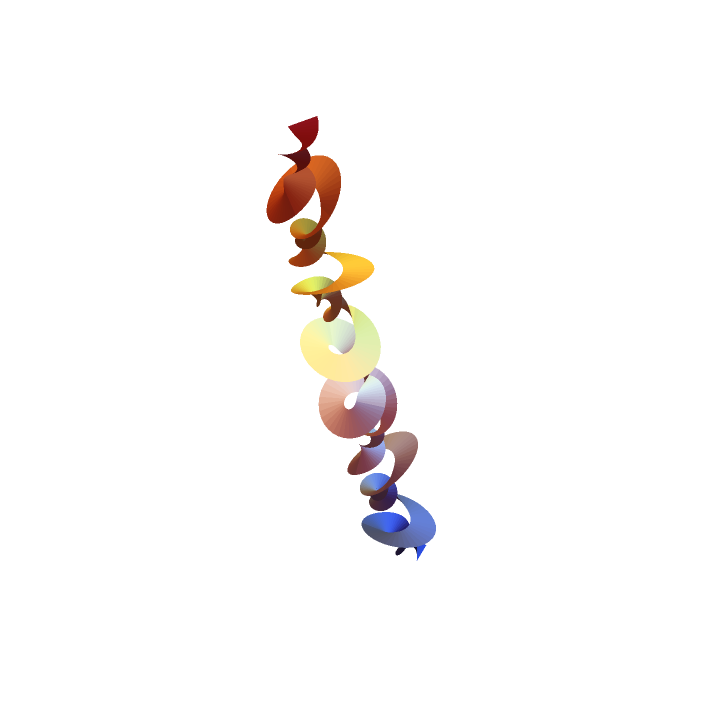A function varying rapidly needs small discrete steps to plot smoothly:

In[5]:=
ResourceFunction["Intrinsic3DCurve"][#^2 &, 10 &, 2.25, .5, 1., 0.01, 560]
Out[5]=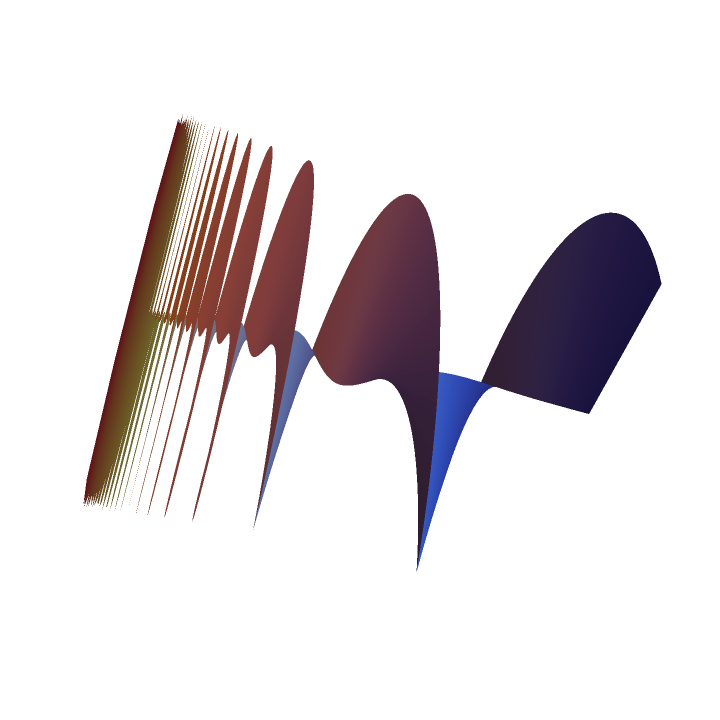

Avoid undefined values like log(0):

In[6]:=
ResourceFunction["Intrinsic3DCurve"][ Log[# + .1] &, Sin, 2.25, .5, 1., 0.01, 600]
Out[6]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 07 March 2019

Related Resources

License Information