Function Repository Resource:

InequalityPlot

Source Notebook

Plot a set of inequalities distinguishing between different regions

Contributed by: Enrique Zeleny, Wolfram|Alpha Math Team

ResourceFunction["InequalityPlot"][ineqs,x]

plots a set of inequalities distinguishing between different regions and choosing ranges automatically.

ResourceFunction["InequalityPlot"][ineqs,{x,x₀,x_f}]

plots a set of inequalities with one variable distinguishing between different regions from x₀ to x_f.

ResourceFunction["InequalityPlot"][ineqs,{x,y}]

plots a set of inequalities with two independent variables.

ResourceFunction["InequalityPlot"][ineqs,{x,x₀,x_f},{y,y₀,y_f}]

plots a set of inequalities with two variables from x₀ to x_f and from y₀ to y_f.

ResourceFunction["InequalityPlot"][ineqs,{x,y,z}]

plots a set of inequalities with three independent variables.

ResourceFunction["InequalityPlot"][ineqs,{x,x₀,x_f},{y,y₀,y_f},{z,z₀,z_f}]

plots a set of inequalities with three variables from x₀ to x_f, from y₀ to y_f and from z₀ to z_f.

Details

InequalityPlot has the same options as ContourPlot and RegionPlot.

Without explicit intervals, InequalityPlot uses SuggestPlotRange.

Examples

Basic Examples (4)

Inequalities in one dimension:

In[1]:=

Out[1]=

Inequalities in two dimensions:

In[2]:=

Out[2]=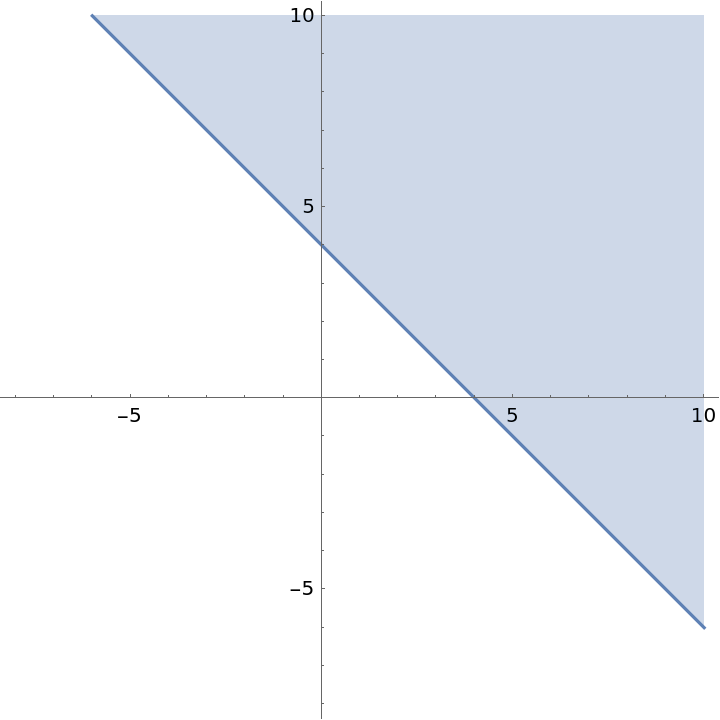

Intersection of a couple of lines:

In[3]:=

Out[3]=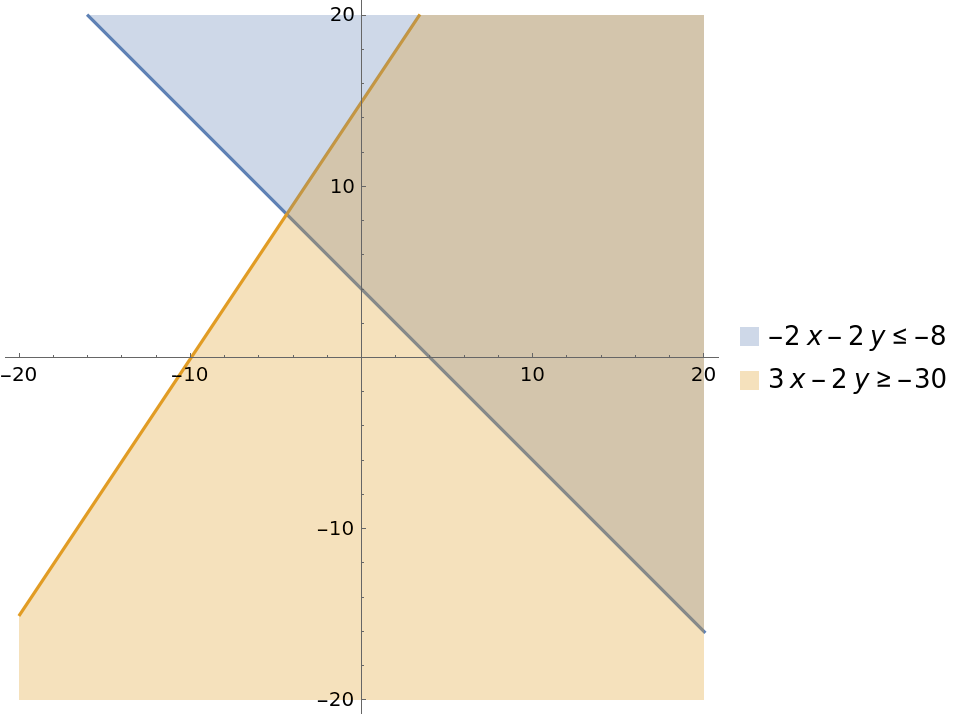

Dashed lines represent strict inequalities like Less and Greater:

In[4]:=

Out[4]=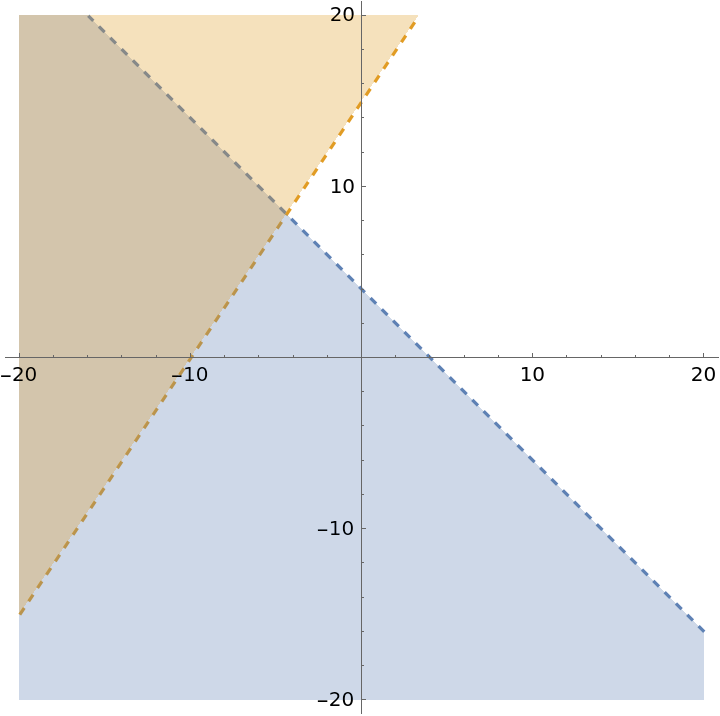

Without an explicit interval, the range is chosen automatically:

In[5]:=

$ResourceFunction["InequalityPlot"][ 3 x^2 + y > 0 && x - 5 y >= 0, {x, y}]$

Out[5]=

Scope (9)

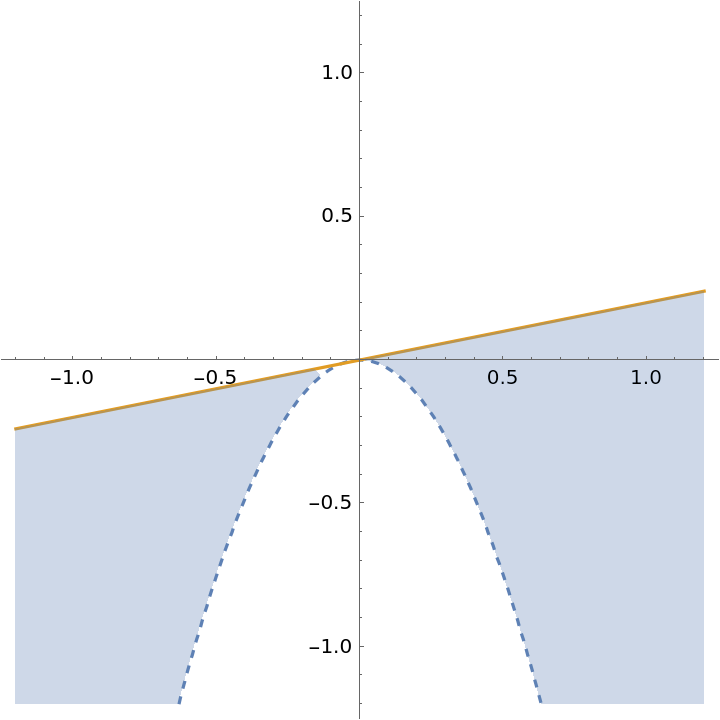Regions generated by several lines:

In[6]:=

Out[6]=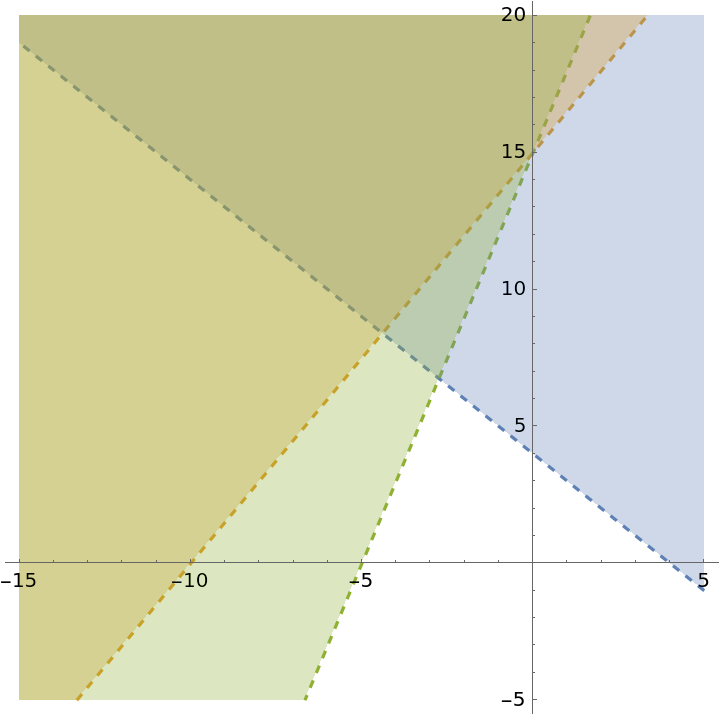

See many regions defined by two parabolas:

In[7]:=

$Manipulate[ ResourceFunction["InequalityPlot"][ Evaluate@op[y + 10 < (x - 2)^2, -y + 1 < x^2], {x, -10, 20}, {y, -20, 10}, MaxRecursion -> 5], {op, {And, Or, Xor, Implies, Nand, Nor}}]$

Out[7]=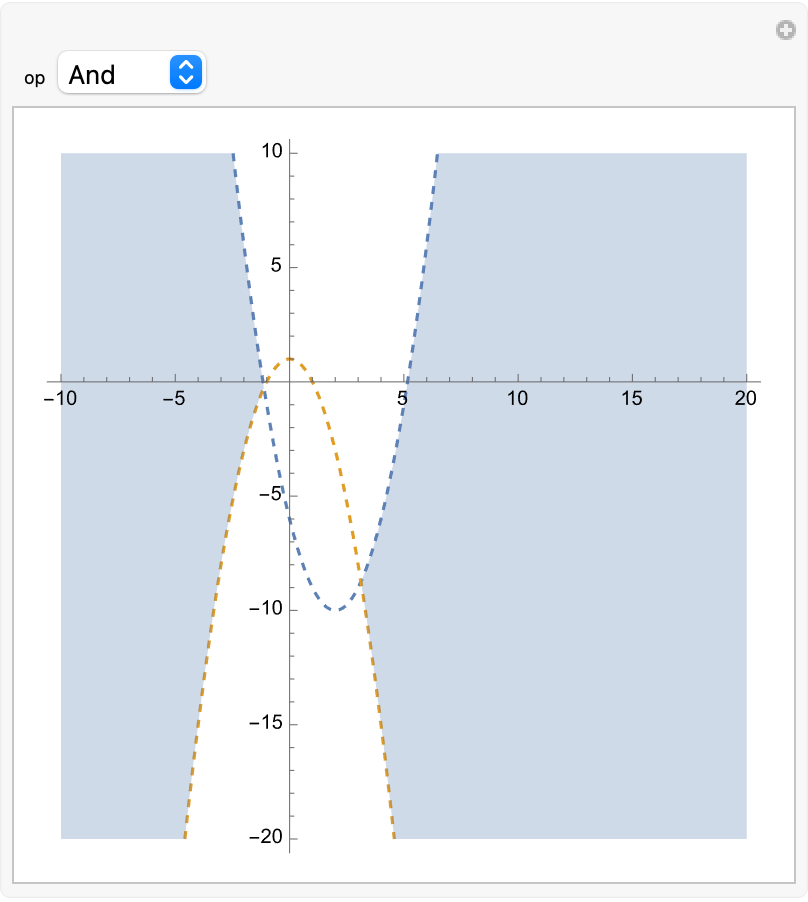

Higher degree region:

In[8]:=

$With[{a = 2, b = 1, c = 2, n = 3}, ResourceFunction[ "InequalityPlot"][{a x^(1 + 2 n) - c x^n y^n + b y^(1 + 2 n) < 0 && 3 x - 5 y >= -1}, {x, -.6, .7}, {y, -.8, .8}, MaxRecursion -> 5]]$

Out[8]=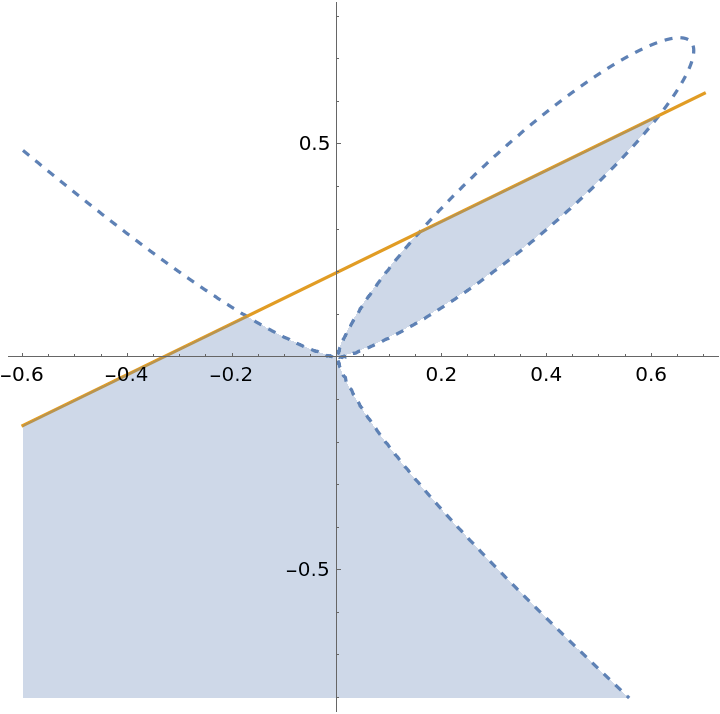

Limits to infinity:

In[9]:=

$ResourceFunction["InequalityPlot"][ x^2 < y^3 + 1 && y^2 < x^3 + 1, {x, -Infinity, Infinity}, {y, -Infinity, Infinity}]$

Out[9]=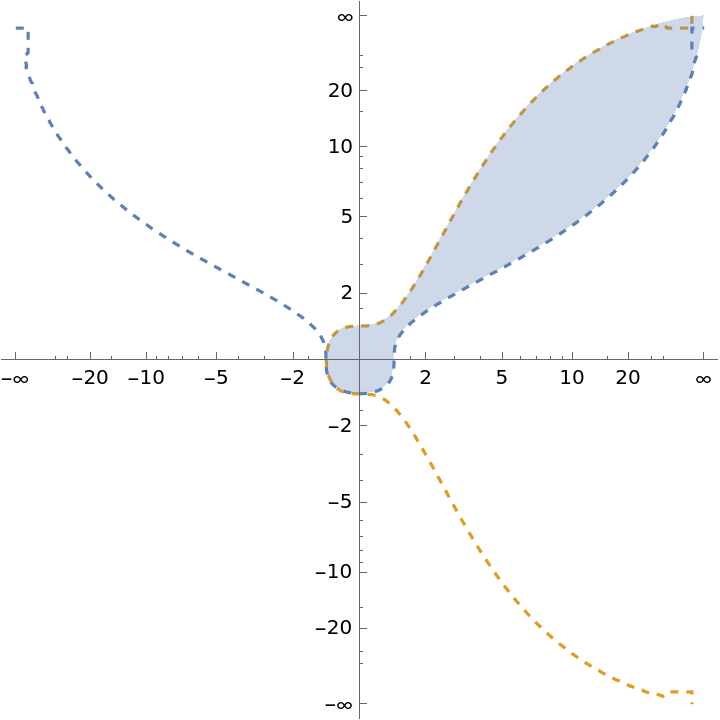

Specify the scaling with ScalingFunctions:

In[10]:=

$ResourceFunction["InequalityPlot"][ x^2 y < y^2 + x^2, {x, 0, 100}, {y, 0, 100}, ScalingFunctions -> {"Log", "Log"}]$

Out[10]=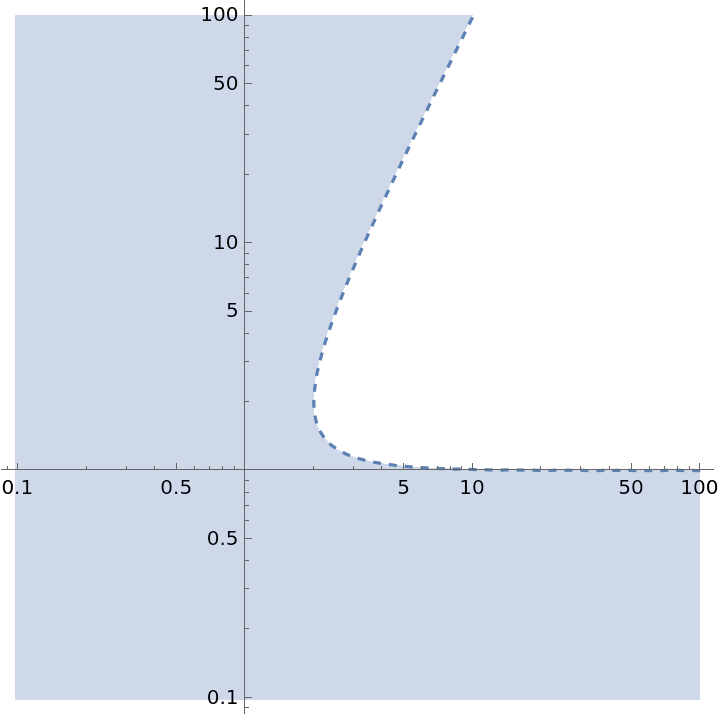

Visualize a 3D region:

In[11]:=

Out[11]=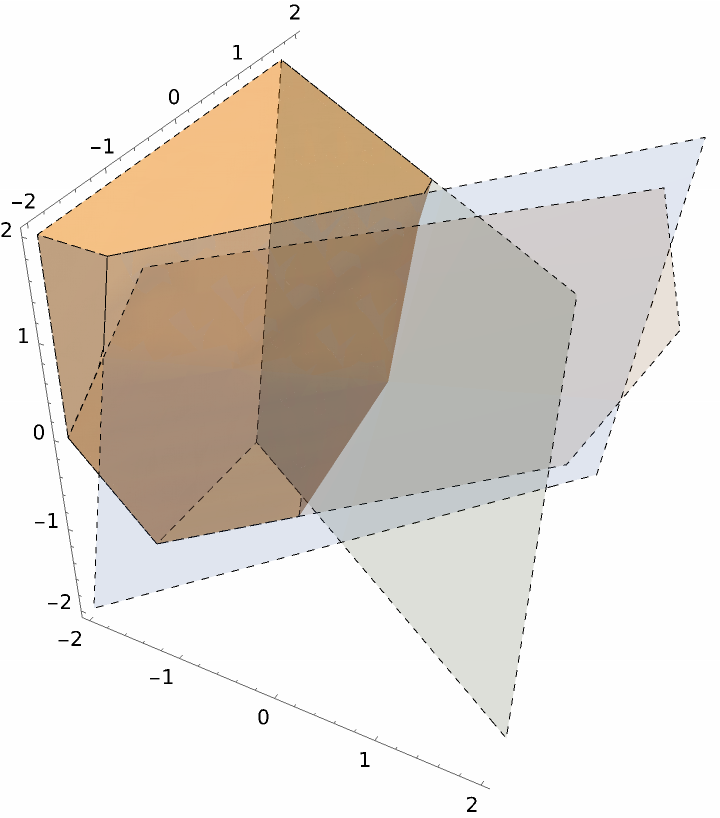

Without explicit intervals:

In[12]:=

Out[12]=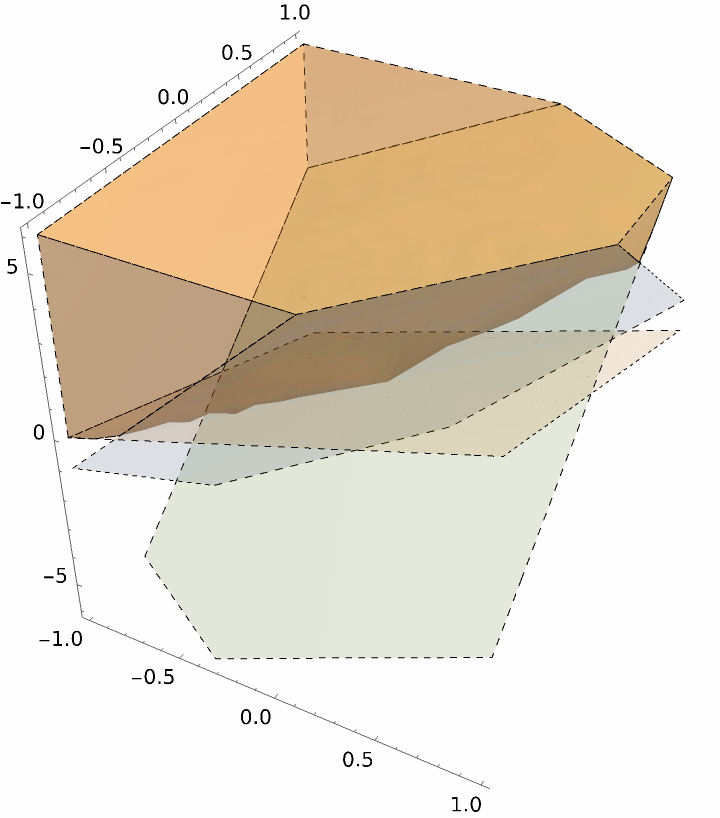

Three intersecting cylinders:

In[13]:=

$ResourceFunction["InequalityPlot"][ x^2 + y^2 <= 1 && x^2 + z^2 <= 1 && y^2 + z^2 <= 1, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, PlotStyle -> Yellow, Mesh -> 5, PlotPoints -> 50]$

Out[13]=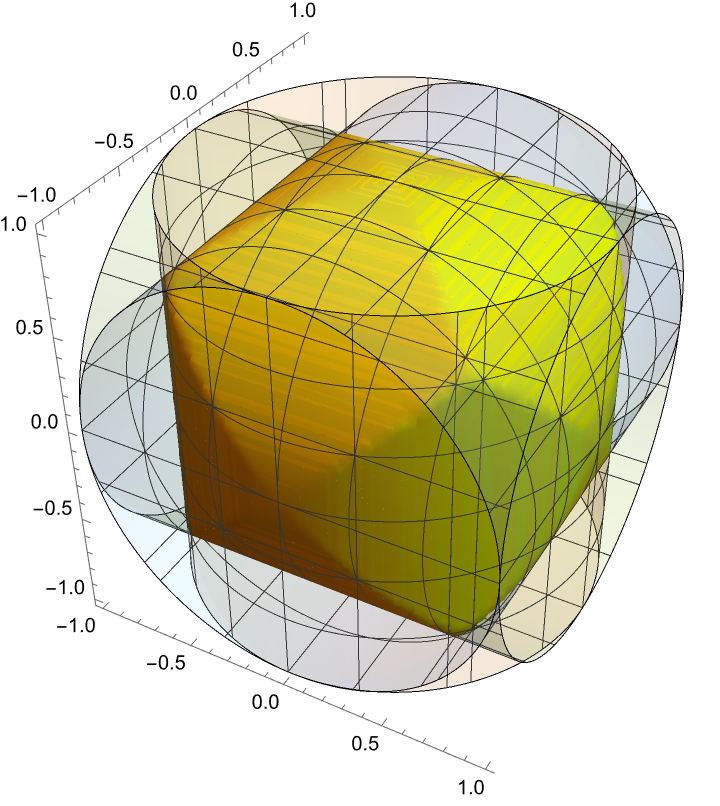

Region defined by planes:

In[14]:=

ResourceFunction[
"InequalityPlot"][-.5 < x <= .5 && -.5 < y < .5 && -.5 < z < .5, {x, y, z}, ContourStyle -> Table[{Directive[ColorData[10, "ColorList"][[i]], Opacity[.5]]}, {i,
6}], Lighting -> "Neutral", PlotLegends -> True]

Out[14]=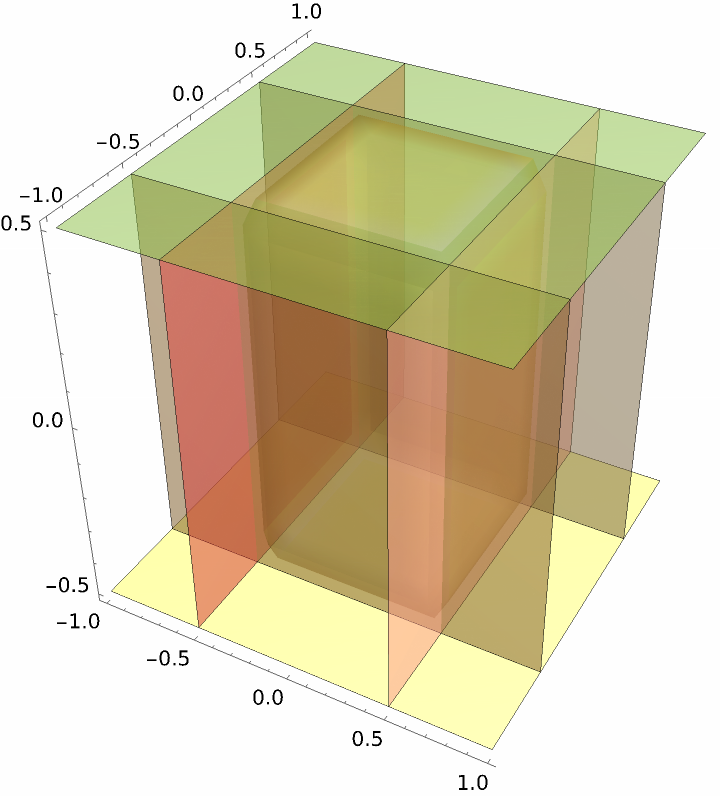

Region defined by two paraboloids:

In[15]:=

$ResourceFunction["InequalityPlot"][ x^2 + y^2 - z < 1 && x^2 + y^2 + z > 1, {x, -3, 3}, {y, -3, 3}, {z, -2, 2}, PlotPoints -> 50, MaxRecursion -> 5]$

Out[15]=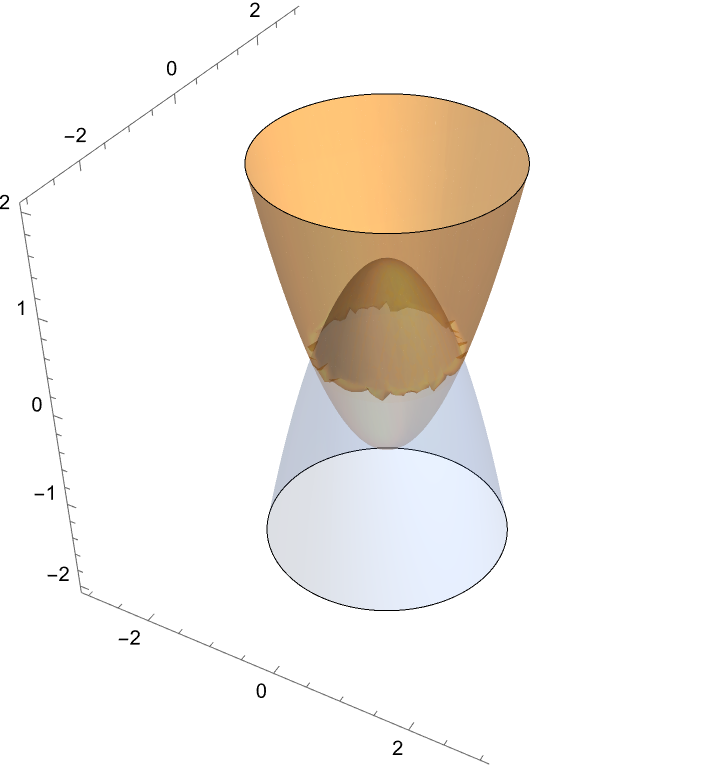

Higher order region:

In[16]:=

$ResourceFunction["InequalityPlot"][ 3 x^2 + y^3 - z^2 > 0 && x - 5 y >= z, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}]$

Out[16]=

Random 3D region:

In[17]:=

$ResourceFunction["InequalityPlot"][ Table[(x - RandomReal[{-1, 1}])^2 + (y - RandomReal[{-1, 1}])^2 + (z - RandomReal[{-1, 1}])^2 <= 1, {3}], {x, -2, 2}, {y, -2, 2}, {z, -2, 2}]$

Out[17]=

Options (9)

PlotLegends (1)

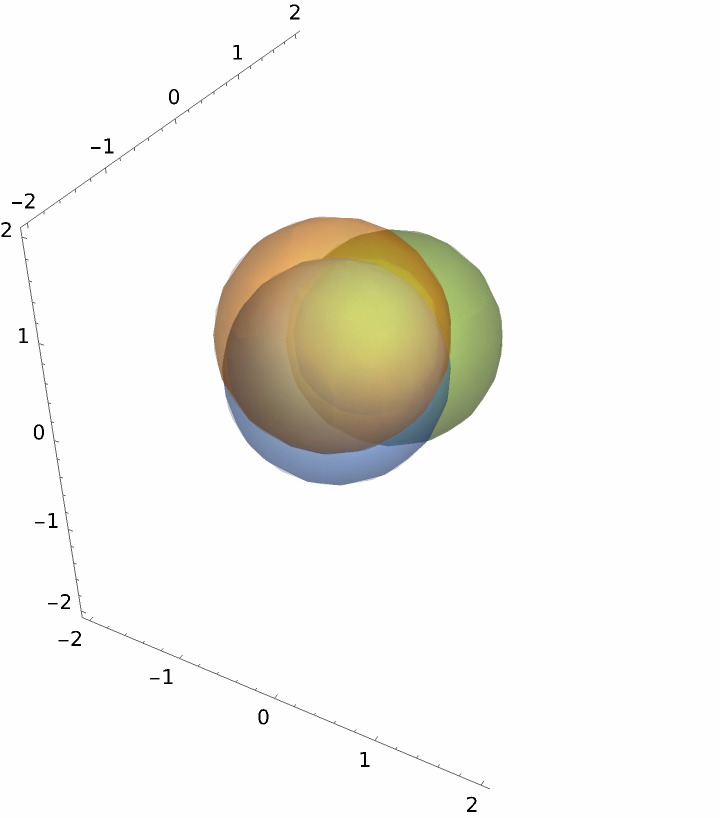Do not show legends:

In[18]:=

Out[18]=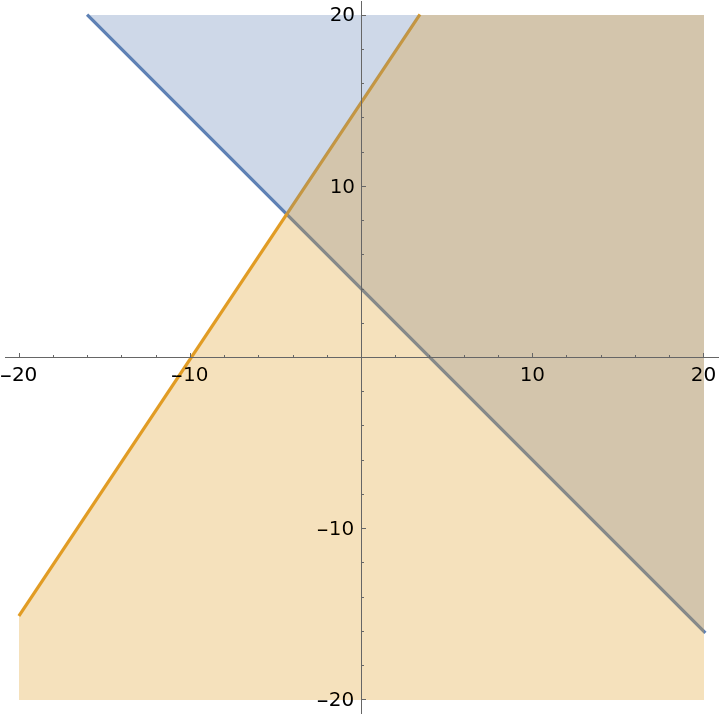

ShowTooltips (1)

Do not show tooltips:

In[19]:=

Out[19]=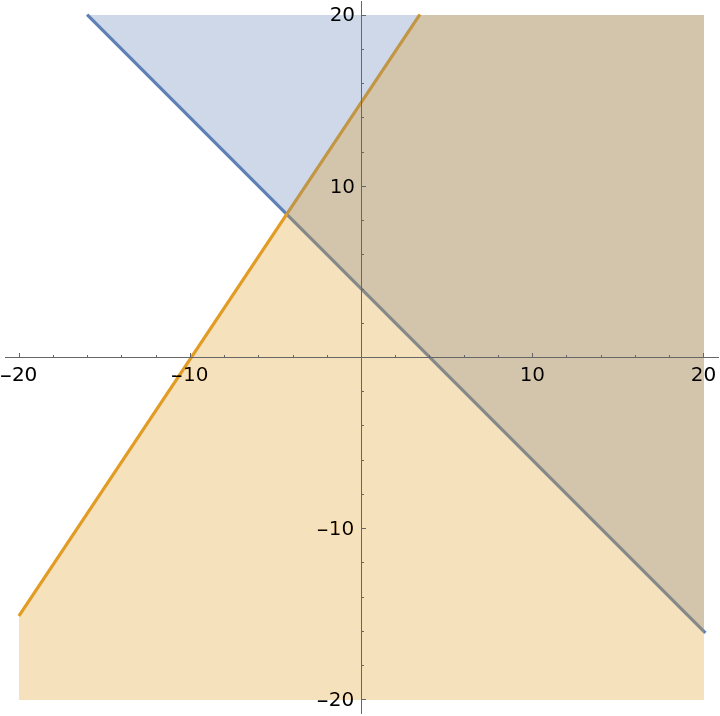

InequalityLegends (1)

A Venn diagram:

In[20]:=

$setineqs = With[{ineqs = {(0.25 + x)^2 + (0.25 + y)^2 <= 1, (-0.25 + x)^2 + (0.25 + y)^2 <= 1, x^2 + (-0.25 + y)^2 <= 1}}, MapAt[Not, And @@@ Table[{ineqs[[1]], ineqs[[2]], ineqs[[3]]}, {8}], Position[Sort[Tuples[{y, n}, 3], Count[#, y] > Count[#2, y] &], y]]];$

In[21]:=

labels = Text @@@ MapThread[
List, {StringJoin @@@ Rest@Subsets[{"A", "B", "C"}], RegionCentroid@Region[ImplicitRegion[#, {x, y}]] & /@ Rest@setineqs}];

In[22]:=

Out[22]=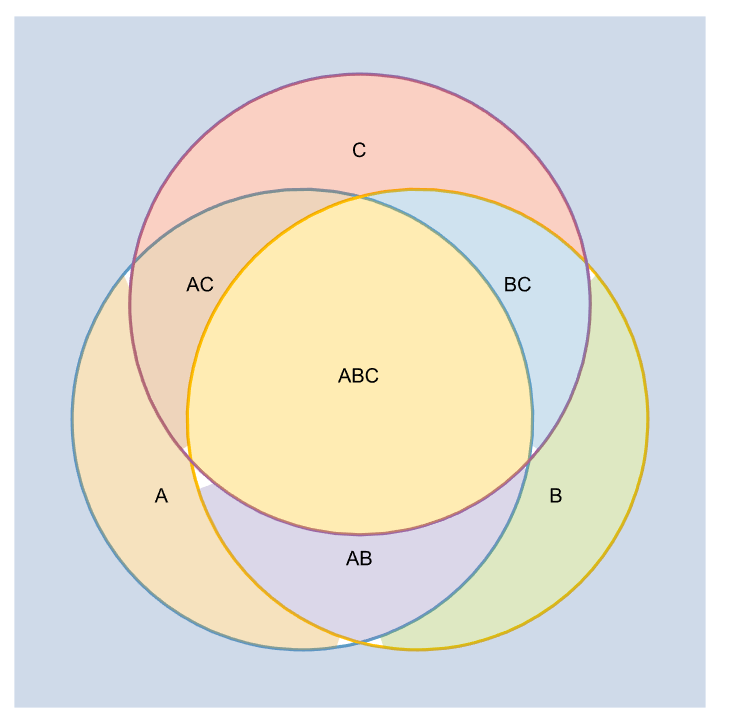

AllSubregions (6)

Define inequalities for overlapping disks which create random subregions:

In[23]:=

$ineqs = Table[(x - RandomReal[])^2 + (y - RandomReal[])^2 <= 1, {4}];$

In[24]:=

In[25]:=

$labels = Text @@@ DeleteCases[ MapThread[ List, {StringJoin @@@ Rest@Subsets[{"A", "B", "C", "D"}], With[{rc = RegionCentroid@Region[ImplicitRegion[#, {x, y}]]}, If[MatchQ[rc, {__?NumericQ}], rc, {}]] & /@ Rest@setineqs}], {_, {}}];$

Use "AllSubregions"→True to include distinct colors for each subregion in the plot:

In[26]:=

Show[ResourceFunction["InequalityPlot"][
Evaluate@ineqs, {x, -1, 2}, {y, -1, 2}, "AllSubregions" -> True, "InequalityLegends" -> "Mouse", MaxRecursion -> 5, Axes -> False], Epilog -> labels, Axes -> False]

Out[26]=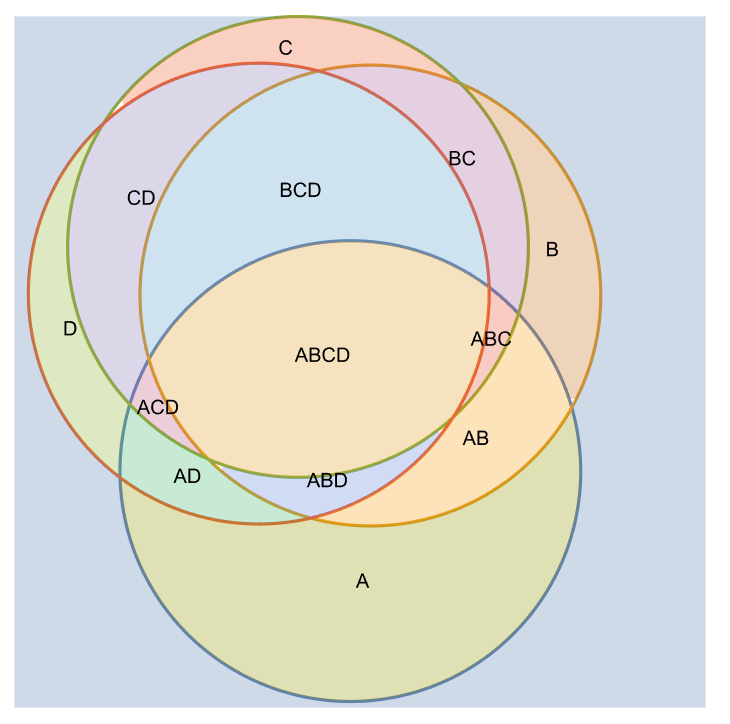

Random 3D region:

In[27]:=

$ResourceFunction["InequalityPlot"][ Table[(x - RandomReal[])^2 + (y - RandomReal[])^2 + (z - RandomReal[])^2 < 1, {3}], {x, -1, 2}, {y, -1, 2}, {z, -1, 2}, "AllSubregions" -> True, PlotStyle -> (Directive[Opacity[.3], #] & /@ {White, Blue, Red, Yellow, Magenta, Green, Cyan, Orange}), MaxRecursion -> 5]$

Out[27]=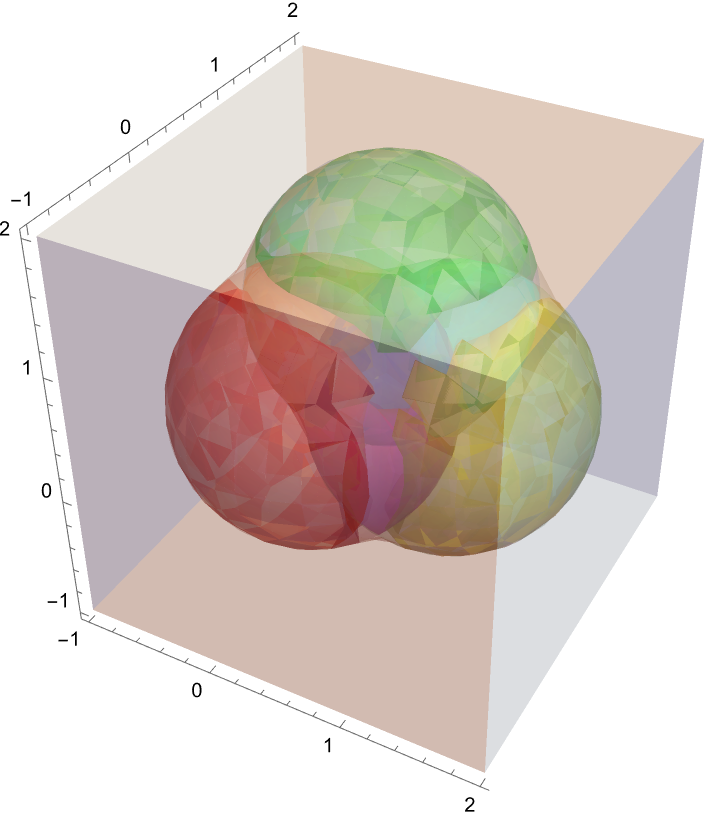

Specify the contour styles:

In[28]:=

Out[28]=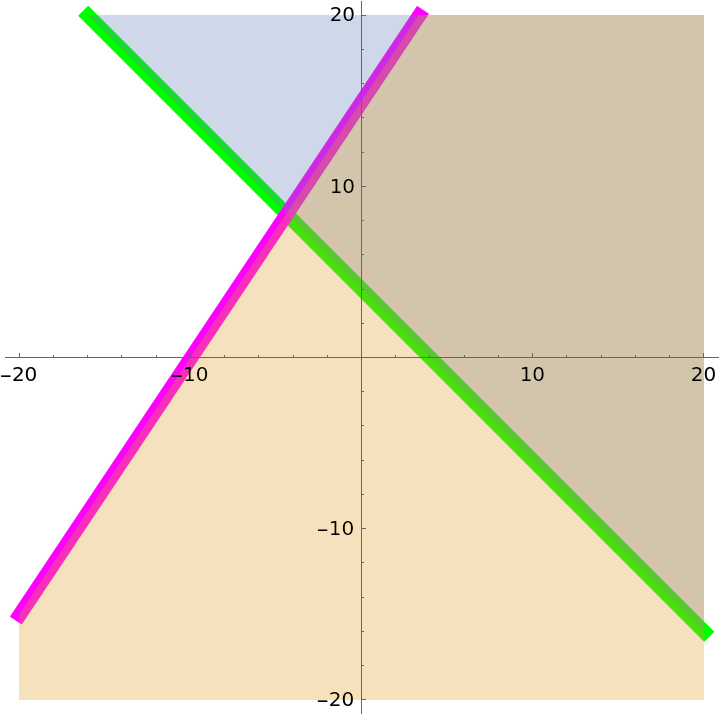

Change the styles for the mesh:

In[29]:=

Out[29]=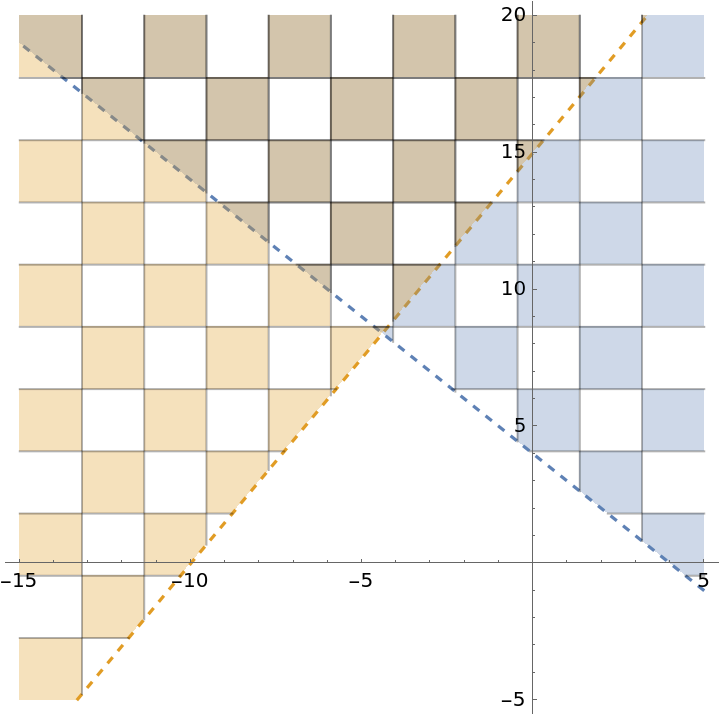

An inequality over a region:

In[30]:=

$ResourceFunction[ "InequalityPlot"][{-2 x - 2 y < -4 && (x + 5)^2 + (y - 5)^2 < 20, 3 x - 2 y < -30 && (x + 5)^2 + (y - 5)^2 < 20}, {x, -10, 0}, {y, 0, 10}, RegionFunction -> ((#1 + 5)^2 + (#2 - 5)^2 < 20 &)]$

Out[30]=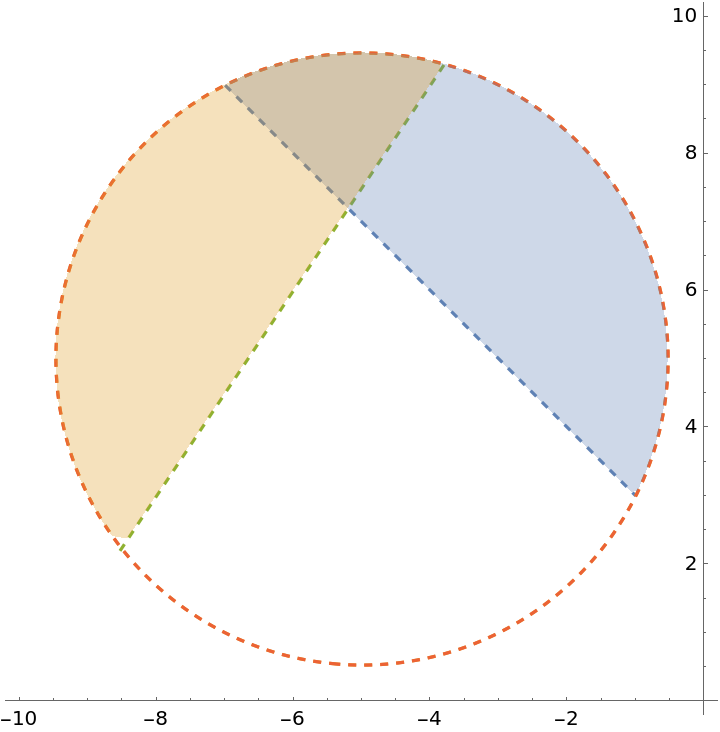

Modify the plot style:

In[31]:=

$ResourceFunction[ "InequalityPlot"][{-x^2 y^3 + (-1 + x^2 + y^2)^3 <= 0, -(x - 1)^2 y^3 + (-1 + (x - 1)^2 + y^2)^3 <= 0}, {x, -1.25, 2.25}, {y, -1.75, 1.75}, PlotStyle -> {{Opacity[.5], Blue}, {Opacity[.5], Red}}, Axes -> False, MaxRecursion -> 5]$

Out[31]=

Properties and Relations (2)

A region between curves:

In[32]:=

$ResourceFunction["InequalityPlot"][ x > y && x^2 < y, {x, 0, 1}, {y, 0, 1}]$

Out[32]=

Compute the area using the resource function AreaBetweenCurves:

In[33]:=

$ResourceFunction["AreaBetweenCurves"][{x, x^2}, {x, 0, 1}]$

Out[33]=

Neat Examples (2)

Control the region included (sometimes a particular intersection does not exist):

In[34]:=

$ineqs = Table[(x - RandomReal[])^2 + (y - RandomReal[])^2 <= 1, {4}];$

In[35]:=

Manipulate[
ResourceFunction["InequalityPlot"][
Evaluate[Not /@ And @@ MapAt[Not, ineqs, List /@ sets]],
{x, -2, 2}, {y, -2, 2}, Axes -> False, MaxRecursion -> 5, PlotLabel -> (Not /@ And @@ MapAt[Not, {"A", "B", "C", "D"}, List /@ sets])],
{sets, {1 -> "A", 2 -> "B" , 3 -> "C", 4 -> "D"}}, ControlType -> TogglerBar]

Out[35]=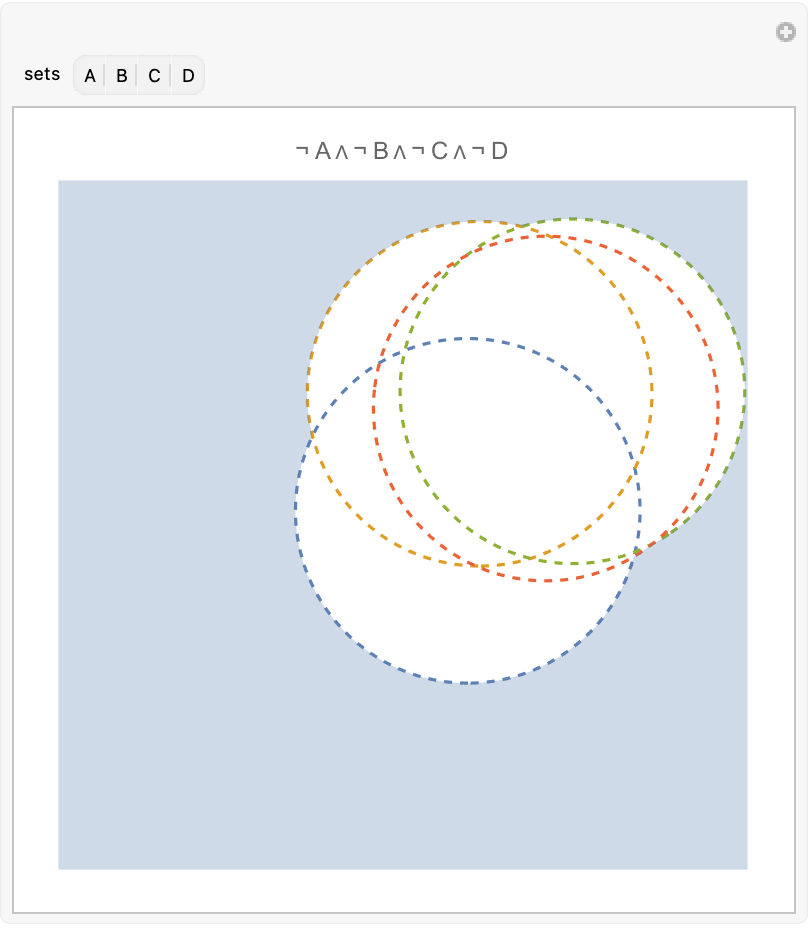

See all subsets in a grid:

In[36]:=

$ineqs2 = Table[(x - RandomReal[])^2 + (y - RandomReal[])^2 <= 1, {4}]; GraphicsGrid[ Partition[(ResourceFunction[ "InequalityPlot"][#1, {x, -1, 2}, {y, -1, 2}, MaxRecursion -> 5, Axes -> False] &) /@ With[{subeq = Rest@Subsets[ineqs2]}, Join[{! Or @@ Last@subeq}, And @@@ Thread[{(! And @@ Complement[ineqs2, #1] &) /@ Most@subeq, And @@@ Most@subeq}], {And @@ Last@subeq}]], 4]]$

Out[36]=

Publisher

Enrique Zeleny

Requirements

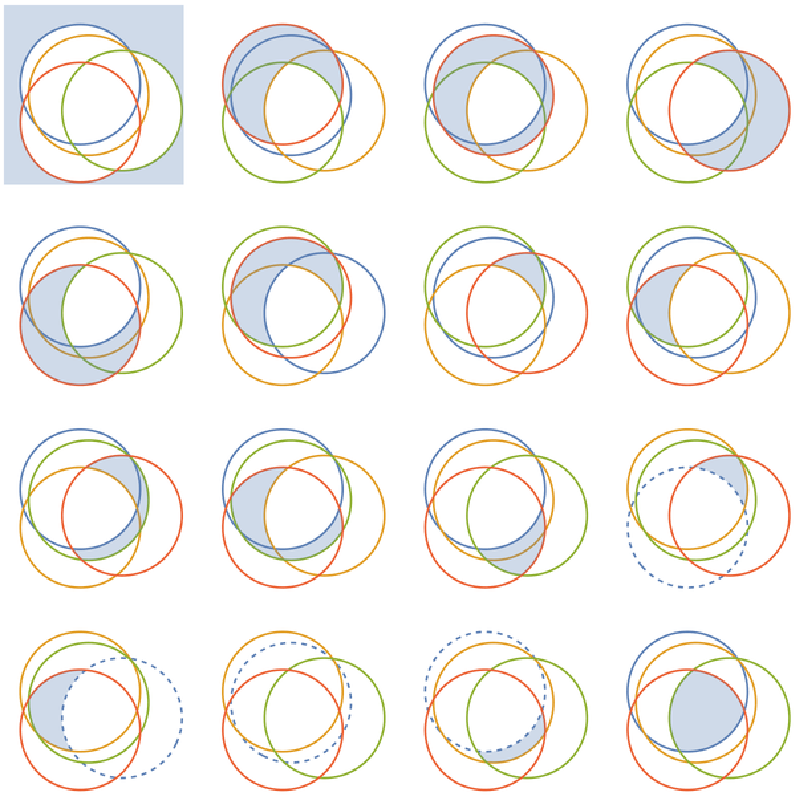Wolfram Language 13.0 (December 2021) or above

Version History

1.0.0 – 17 November 2023

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

InequalityPlot

Details

Examples

Basic Examples (4)

Scope (9)

Options (9)

PlotLegends (1)

ShowTooltips (1)

InequalityLegends (1)

AllSubregions (6)

Properties and Relations (2)

Neat Examples (2)

Publisher

Related Links

Requirements

Version History

Related Resources

License Information

InequalityPlot

Details

Examples

Basic Examples (4)

Scope (9)

Options (9)

PlotLegends (1)

ShowTooltips (1)

InequalityLegends (1)

AllSubregions (6)

Properties and Relations (2)

Neat Examples (2)

Publisher

Related Links

Requirements

Version History

Related Resources

Related Symbols

License Information