Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find the location at which a picture was taken
ResourceFunction["ImageGeoLocation"][img] returns the estimated GeoLocation[…] at which img was taken. | |
ResourceFunction["ImageGeoLocation"][img,n] returns the first n probable locations. | |
ResourceFunction["ImageGeoLocation"][img,n,"Probabilities"] returns the locations together with their probabilities. | |
ResourceFunction["ImageGeoLocation"][{img1,img2,…},…] estimates multiple locations at once. |
Find the location at which a picture was taken:
| In[1]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/a6ff96a5-1885-41b9-b53b-e4bb6449fbed"]](https://www.wolframcloud.com/obj/resourcesystem/images/6f4/6f4a5daf-b930-4496-8fdf-d4ea00630e46/1238908606c951ee.png) |
| Out[1]= |
Find multiple location candidates:
| In[2]:= |
| Out[2]= |
Map them:
| In[3]:= |
| Out[3]= | 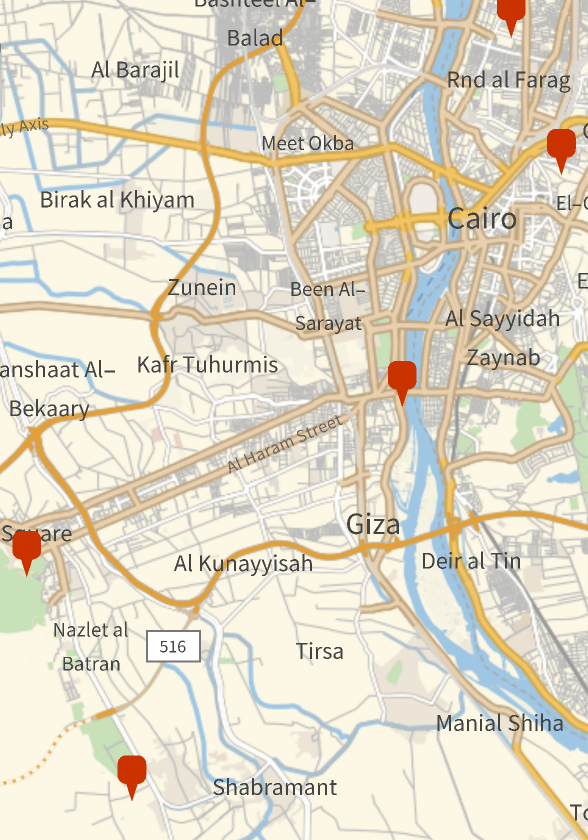 |
Predict one location:
| In[4]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/70773b9d-65ab-4ab3-9df2-3fe0599970fc"]](https://www.wolframcloud.com/obj/resourcesystem/images/6f4/6f4a5daf-b930-4496-8fdf-d4ea00630e46/3a29bfbbeee7f5c8.png) |
| Out[4]= |
Return the first n most probable locations:
| In[5]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/64356d01-e2d4-463a-8a8e-1b41985c55e5"]](https://www.wolframcloud.com/obj/resourcesystem/images/6f4/6f4a5daf-b930-4496-8fdf-d4ea00630e46/47302eb2ca9d04c4.png) |
| Out[5]= |
Predict locations for multiple images:
| In[6]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/ca5d879f-957a-4076-a0df-15878afb94d7"]](https://www.wolframcloud.com/obj/resourcesystem/images/6f4/6f4a5daf-b930-4496-8fdf-d4ea00630e46/112f8563e02ded4b.png) |
| Out[6]= |
Return the first n most probable locations for multiple images:
| In[7]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/7af117de-85ca-4e4c-857d-ab363d3d7406"]](https://www.wolframcloud.com/obj/resourcesystem/images/6f4/6f4a5daf-b930-4496-8fdf-d4ea00630e46/5f59342535b69418.png) |
| Out[7]= |  |
Return locations together with their probabilities:
| In[8]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/bdba0f70-0b53-470c-a490-f7b5314ceb0b"]](https://www.wolframcloud.com/obj/resourcesystem/images/6f4/6f4a5daf-b930-4496-8fdf-d4ea00630e46/696ff674b0413687.png) |
| Out[8]= |  |
| In[9]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/1dd85709-bc4b-430f-8294-e61ceb218231"]](https://www.wolframcloud.com/obj/resourcesystem/images/6f4/6f4a5daf-b930-4496-8fdf-d4ea00630e46/6cc27b01a1d144e1.png) |
| Out[9]= |  |
In places with high population density, very fine-grained predictions are possible. Consider the following four landmarks in Paris:
| In[10]:= | ![landmarks = EntityValue[{Entity["Building", "EiffelTower::5h9w8"], Entity["Building", "TheLouvre::vqy3g"], Entity["Building", "NotreDameCathedral::95fcw"], Entity["Building", "ArcDeTriomphe::92x88"]}, "Image", "EntityAssociation"]](https://www.wolframcloud.com/obj/resourcesystem/images/6f4/6f4a5daf-b930-4496-8fdf-d4ea00630e46/1b664c4a6345009e.png) |
| Out[10]= |  |
Predict the location of the four landmarks:
| In[11]:= |
| Out[11]= |  |
Plot the locations on the map:
| In[12]:= |
| Out[12]= | 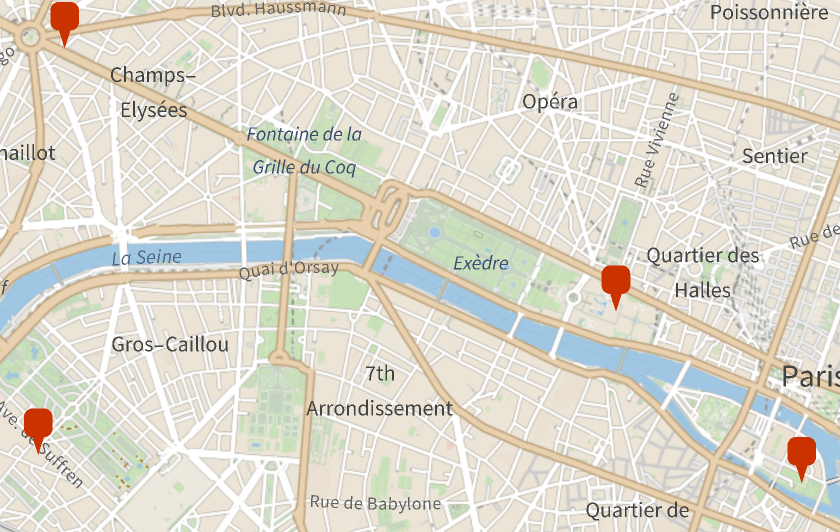 |
Compare to the locations from Wolfram|Alpha:
| In[13]:= |
| Out[13]= |  |
Find the most probable locations for an image of white cliffs:
| In[14]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/77a42f5c-e513-4c14-bbef-f8f0737b48e8"]](https://www.wolframcloud.com/obj/resourcesystem/images/6f4/6f4a5daf-b930-4496-8fdf-d4ea00630e46/4921aee64d06a5a5.png) |
| Out[14]= |  |
Plot them in a bubble chart where the radius is given by the probability value:
| In[15]:= |
| Out[15]= | 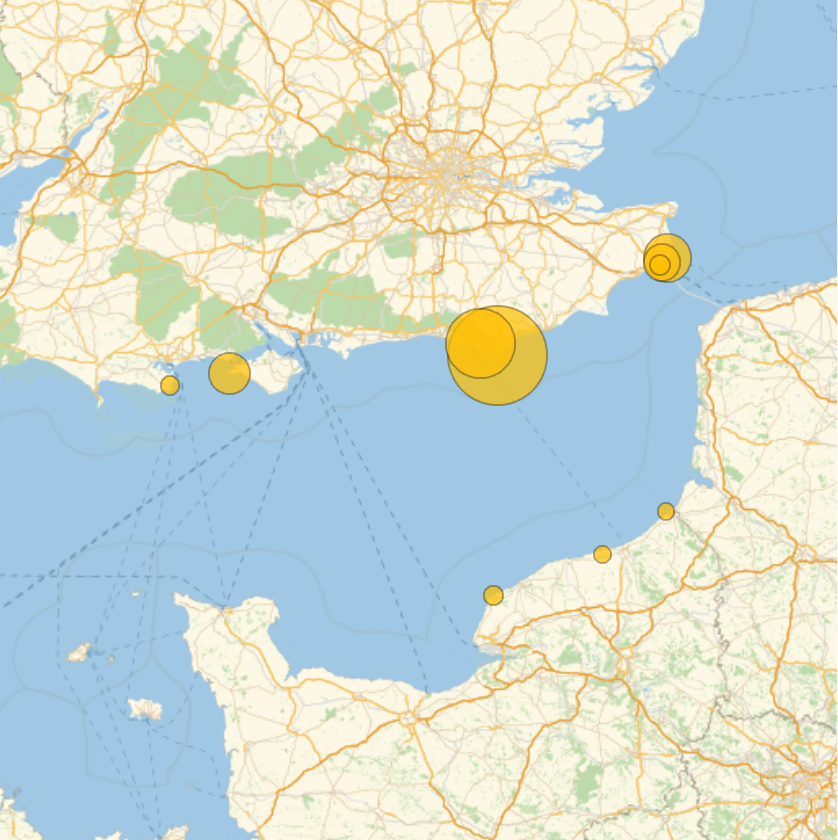 |
This work is licensed under a Creative Commons Attribution 4.0 International License