Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Represent a hyperbolic polygon embedded in the Poincaré disk
ResourceFunction["HyperbolicPoincarePolygon"][{p1,…,pn}] represents a filled hyperbolic polygon with points pi, embedded in the Poincaré disk. |
A random hyperbolic triangle:
| In[1]:= |
Show the hyperbolic triangle in the Poincaré disk:
| In[2]:= |
| Out[2]= |  |
Use directives to style the polygon:
| In[3]:= |
| In[4]:= |
| Out[4]= |  |
| In[5]:= |
| Out[5]= |  |
A concave polygon:
| In[6]:= | ![Graphics[{{Thick, Circle[]}, {Brown, ResourceFunction[
"HyperbolicPoincarePolygon"][{{-0.5, -0.5}, {0., 0.}, {0.5, -0.5}, {0., 0.8}}]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/628/628f5886-81ef-497c-8200-64eb236446b8/2d1f8dd46fe85862.png) |
| Out[6]= |  |
A triangle with a side that goes through the origin:
| In[7]:= |
| Out[7]= |  |
A triangle with points at infinity:
| In[8]:= | ![Graphics[{{Thick, Circle[]}, {Green, ResourceFunction[
"HyperbolicPoincarePolygon"][{{0.8, 0.6}, {-0.6, 0.8}, {0.2, -0.2}}]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/628/628f5886-81ef-497c-8200-64eb236446b8/09dd75579c24b5a3.png) |
| Out[8]= |  |
All vertices of HyperbolicPoincarePolygon must lie within the unit disk:
| In[10]:= |
| Out[10]= |
Show a regular hyperbolic polygon in the Poincaré disk:
| In[11]:= |
| In[12]:= | ![regularHyperbolicPolygon[n_, r_, cent_ : {0, 0}] := Module[{c, poly, v},
v = Tanh[r/2] Exp[I (\[Pi]/n - \[Pi]/2)];
poly = NestList[hyperbolicRotate[#, {0, (2 \[Pi])/n}] &, v, n - 1];
c = cent . {1, I};
If[Abs[c] > 0,
poly = (poly + c)/(1 + Conjugate[c] poly)];
ResourceFunction["HyperbolicPoincarePolygon"][ReIm[N[poly]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/628/628f5886-81ef-497c-8200-64eb236446b8/6a1b5ce564dff3f7.png) |
| In[13]:= | ![Manipulate[
Graphics[{{Thick, Circle[]}, {Directive[EdgeForm[Directive[Thick, GrayLevel[0.3]]], FaceForm[ColorData[61, 3]]], regularHyperbolicPolygon[n, r, c]}}, {BaseStyle -> {FilledCurveBoxOptions -> {Method -> {"SplinePoints" -> 18}}}, PlotRange -> 1}], {{n, 3, "number of sides"}, 3, 12,
1}, {{r, 1, "radius"}, 1/10, 5}, {{c, {0, 0}}, Locator}, SaveDefinitions -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/628/628f5886-81ef-497c-8200-64eb236446b8/3b5584c508de0985.png) |
| Out[13]= | 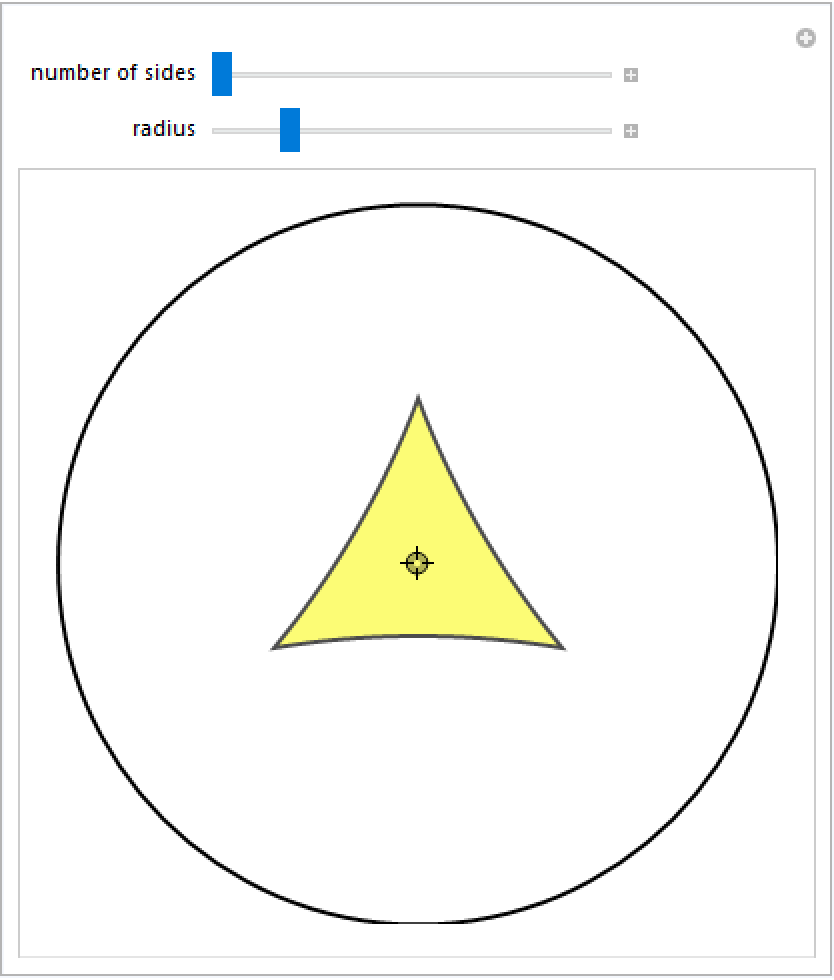 |
This work is licensed under a Creative Commons Attribution 4.0 International License