Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 HyperbolicPoincareLine

Source Notebook

Represent a hyperbolic line segment or polyline embedded in the Poincaré disk

Contributed by: Jan Mangaldan

ResourceFunction["HyperbolicPoincareLine"][{p1,…,pn}]

represents the hyperbolic line segments joining a sequence of points pi, embedded in the Poincaré disk.

Details

ResourceFunction["HyperbolicPoincareLine"] can be used as a graphics primitive.
ResourceFunction["HyperbolicPoincareLine"] returns a JoinedCurve object.
The points pi must all have dimension 2, and must all lie within the unit disk.

Examples

Basic Examples (2) 

A hyperbolic line segment:

In[1]:=
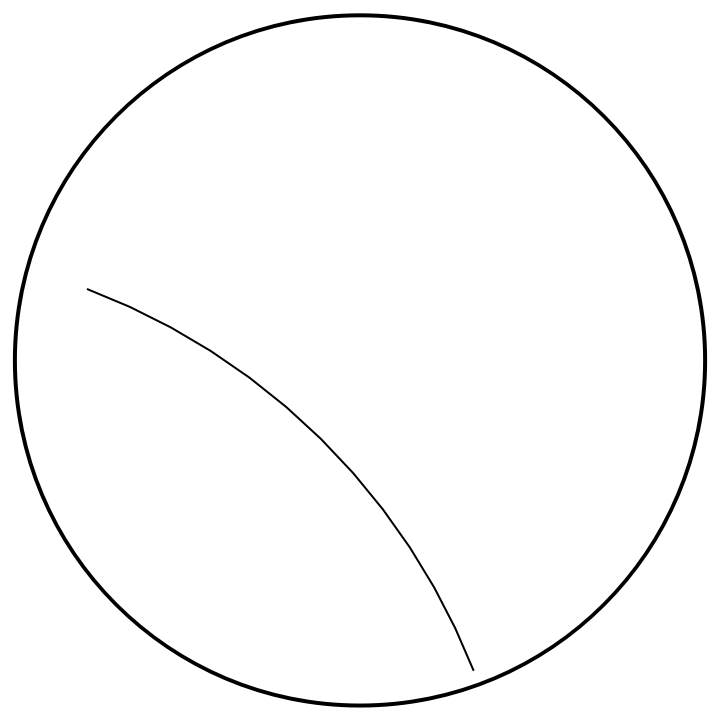
lin = ResourceFunction["HyperbolicPoincareLine"][ RandomPoint[Disk[], 2]];

Show the hyperbolic line segment in the Poincaré disk:

In[2]:=
Graphics[{{Thick, Circle[]}, lin}]
Out[2]=

A hyperbolic polyline:

In[3]:=
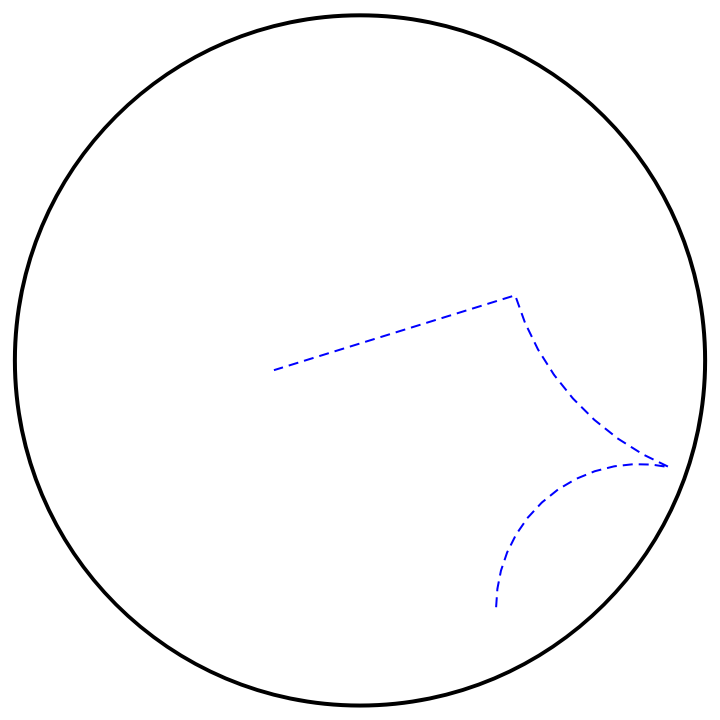
lin = ResourceFunction["HyperbolicPoincareLine"][ RandomPoint[Disk[], 4]];

Show the hyperbolic polyline in the Poincaré disk with styling:

In[4]:=
Graphics[{{Thick, Circle[]}, {Directive[Blue, Dashed], lin}}]
Out[4]=

Scope (3) 

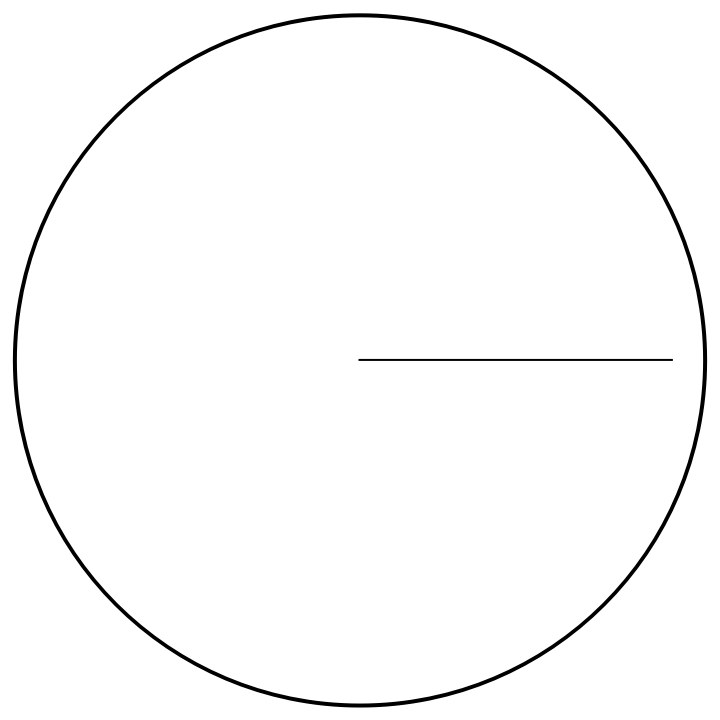
Construct a hyperbolic line segment of given length with one endpoint at the origin:

In[5]:=
With[{r = 3}, Graphics[{{Thick, Circle[]}, ResourceFunction[ "HyperbolicPoincareLine"][{{0, 0}, {Tanh[r/2], 0}}]}]]
Out[5]=

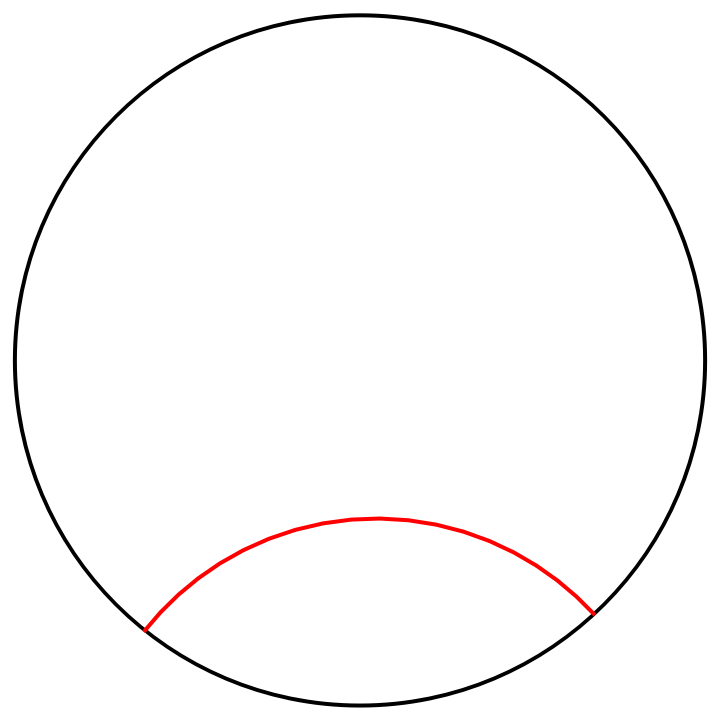
A hyperbolic line segment with endpoints at infinity:

In[6]:=
lin = ResourceFunction["HyperbolicPoincareLine"][ RandomPoint[Circle[], 2]];
In[7]:=
Graphics[{{Thick, Circle[]}, {Directive[Red, Thick], lin}}]
Out[7]=

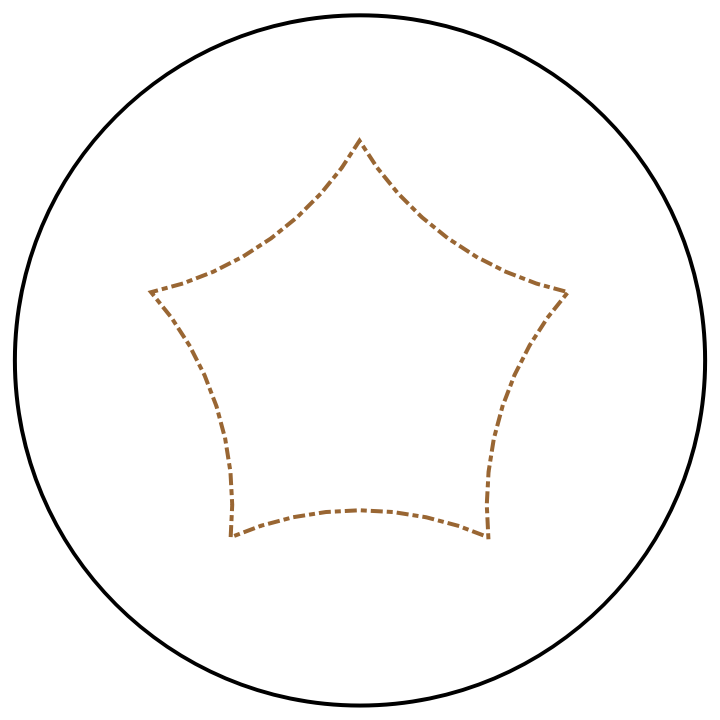
Show the outline of a regular polygon centered at the origin:

In[8]:=
With[{n = 5, r = 3/2}, Graphics[{{Thick, Circle[]}, {Directive[Brown, Thick, DotDashed], ResourceFunction[ "HyperbolicPoincareLine"][{##, #1} & @@ N[CirclePoints[Tanh[r/2], n]]]}}]]
Out[8]=

Properties and Relations (1) 

HyperbolicPoincareLine returns a JoinedCurve object:

In[9]:=
ResourceFunction[ "HyperbolicPoincareLine"][{{0.5, 0.}, {0., 0.5}}] // Head
Out[9]=

Possible Issues (1) 

All vertices of HyperbolicPoincareLine must lie within the unit disk:

In[10]:=
ResourceFunction["HyperbolicPoincareLine"][{{2., 0.}, {0., 0.7}}]
Out[10]=

Neat Examples (1) 

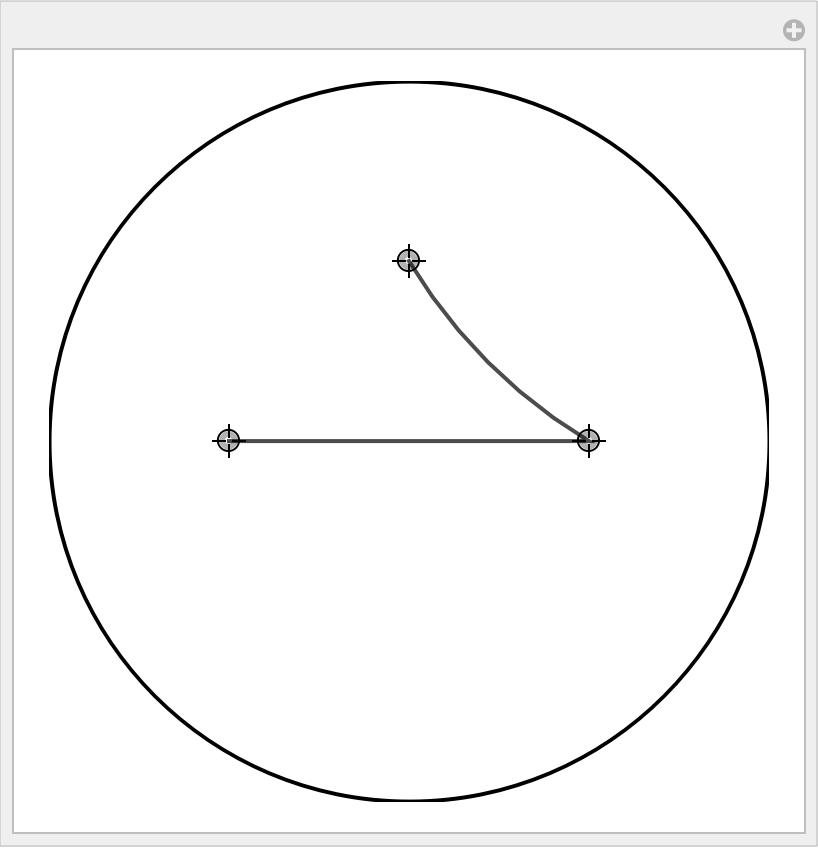
Create a Manipulate of joined points on the Poincaré disk, where points can be added or deleted by Alt-Click:

In[11]:=
Manipulate[pts = Clip[Norm[#], {0, 1}] Normalize[#] & /@ pts; Graphics[{{Thick, Circle[]}, {Directive[Thick, GrayLevel[0.3]], ResourceFunction["HyperbolicPoincareLine"][pts]}}, { BaseStyle -> { FilledCurveBoxOptions -> {Method -> {"SplinePoints" -> 18}}}, PlotRange -> 1}], {{pts, {{-0.5, 0.}, {0.5, 0.}, {0., 0.5}}}, Locator, LocatorAutoCreate -> True}, SaveDefinitions -> True]
Out[11]=

Version History

  • 1.0.0 – 16 March 2021

Related Resources

Author Notes

HyperbolicPoincareLine relies the NURBS representation of a circle arc, which can also easily handle the case where a geodesic representing a segment passes through a diameter of the disk.

License Information