Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Hydrogen
The position-space wavefunction of the hydrogen atom
Contributed by:
Matt Kafker
ResourceFunction["HydrogenWavefunction"][{n,l,m},a,{r,θ,ϕ}] gives the wavefunction for the hydrogen atom with quantum numbers (n,l,m) and Bohr radius a as a function of the spherical coordinates r,θ and ϕ. | |
ResourceFunction["HydrogenWavefunction"][{n,l,m},a,{r,θ,ϕ},Z] gives the hydrogen-like wavefunction with nuclear charge Z. |
Examples
Basic Examples (2)
The hydrogen ground state wavefunction:
| In[1]:= | ![ResourceFunction[
"HydrogenWavefunction"][{1, 0, 0}, a, {r, \[Theta], \[Phi]}]](https://www.wolframcloud.com/obj/resourcesystem/images/ed5/ed55c685-e337-4ac2-8b57-e1ac163b5570/25eb7cd644f08694.png){kind=small} |
| Out[1]= |  |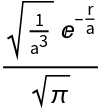
The squared magnitude of the wavefunction gives the probability distribution for finding the electron:
| In[2]:= | ![Simplify[Abs[
ResourceFunction["HydrogenWavefunction"][{3, 1, -1}, a, {r, \[Theta], \[Phi]}]]^2, a > 0 && r > 0 && 0 < \[Phi] < \[Pi] && 0 < \[Theta] < 2 \[Pi]]](https://www.wolframcloud.com/obj/resourcesystem/images/ed5/ed55c685-e337-4ac2-8b57-e1ac163b5570/3f285c29c881eb9f.png) |
| Out[2]= |  |
Scope (3)
Plot radial dependence of a few wavefunctions:
| In[3]:= | ![With[{a = 1}, Plot[Evaluate[
Re /@ {ResourceFunction["HydrogenWavefunction"][{4, 0, 0}, a, {r, 0, \[Phi]}], ResourceFunction["HydrogenWavefunction"][{4, 1, 0}, a, {r, 0, \[Phi]}]}], {r, 0, 25}, {PlotLegends -> {"\!\(\*SubscriptBox[\(\[Psi]\), \(400\)]\)", "\!\(\*SubscriptBox[\(\[Psi]\), \(410\)]\)"}, AxesLabel -> {"r", "\[Psi](r)"}, PlotRange -> All}]]](https://www.wolframcloud.com/obj/resourcesystem/images/ed5/ed55c685-e337-4ac2-8b57-e1ac163b5570/2cfed569aa166f4e.png) |
| Out[3]= |  |
Plot the polar dependence of one wavefunction at various radii:
| In[4]:= | ![With[{a = 1}, PolarPlot[
Evaluate[Table[
Re@ResourceFunction["HydrogenWavefunction"][{3, 2, 0}, a, {r, \[Theta], 0}], {r, 4}]], {\[Theta], 0, 2 \[Pi]}, {AspectRatio -> GoldenRatio^(-1), Axes -> False, PlotLegends -> {"r = 1", "r = 2", "r = 3", "r = 4"}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/ed5/ed55c685-e337-4ac2-8b57-e1ac163b5570/1be0a3014a4df941.png) |
| Out[4]= |  |
Plot the electron probability density for various wavefunctions:
| In[5]:= | ![With[{a = 1}, Table[DensityPlot[
Abs[ResourceFunction["HydrogenWavefunction"][{3, l, 0}, a, {x^2 + y^2, ArcTan[x, y], 0}]]^2, {x, -5, 5}, {y, -5, 5}, {PlotPoints -> 100, PlotLabel -> "n = 3, l = " <> IntegerString[l] <> ", m = 0", FrameLabel -> {"x", "z"}, RotateLabel -> False}], {l, 0, 2}]]](https://www.wolframcloud.com/obj/resourcesystem/images/ed5/ed55c685-e337-4ac2-8b57-e1ac163b5570/40d258772ad33b3b.png) |
| Out[5]= |  |
Properties and Relations (4)
Verify the orthogonality property of HydrogenWavefunction:
| In[6]:= | ![Assuming[a > 0, \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(2 \[Pi]\)]\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(\[Pi]\)]\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(\[Infinity]\)]Conjugate[\*
InterpretationBox[
TagBox[
DynamicModuleBox[{Typeset`open = False},
FrameBox[
PaneSelectorBox[{False->GridBox[{
{
PaneBox[GridBox[{
{
StyleBox[
StyleBox[
AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>",
BoxBaselineShift->-0.25,
BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon",
FontColor->RGBColor[
0.8745098039215686, 0.2784313725490196, 0.03137254901960784]],
ShowStringCharacters->False,
FontFamily->"Source Sans Pro Black",
FontSize->0.6538461538461539 Inherited,
FontWeight->"Heavy",
PrivateFontOptions->{"OperatorSubstitution"->False}],
StyleBox[
RowBox[{
StyleBox["HydrogenWavefunction", "ResourceFunctionLabel",
FontFamily->"Source Sans Pro"], " "}],
ShowAutoStyles->False,
ShowStringCharacters->False,
FontSize->Rational[12, 13] Inherited,
FontColor->GrayLevel[0.1]]}
},
GridBoxSpacings->{"Columns" -> {{0.25}}}],
Alignment->Left,
BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False},
BaselinePosition->Baseline,
FrameMargins->{{3, 0}, {0, 0}}],
ItemBox[
PaneBox[
TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource[
"FEBitmaps", "IconizeCloser"],
ImageSizeCache->{11., {1., 10.}}], False-> DynamicBox[FEPrivate`FrontEndResource[
"FEBitmaps", "IconizeOpener"],
ImageSizeCache->{11., {1., 10.}}]},
Appearance->None,
BaselinePosition->Baseline,
ContentPadding->False,
FrameMargins->0],
Alignment->Left,
BaselinePosition->Baseline,
FrameMargins->{{1, 1}, {0, 0}}],
Frame->{{
RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]}
},
BaselinePosition->{1, 1},
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}},
GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}], True->GridBox[{
{GridBox[{
{
PaneBox[GridBox[{
{
StyleBox[
StyleBox[
AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>",
BoxBaselineShift->-0.25,
BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon",
FontColor->RGBColor[
0.8745098039215686, 0.2784313725490196, 0.03137254901960784]],
ShowStringCharacters->False,
FontFamily->"Source Sans Pro Black",
FontSize->0.6538461538461539 Inherited,
FontWeight->"Heavy",
PrivateFontOptions->{"OperatorSubstitution"->False}],
StyleBox[
RowBox[{
StyleBox["HydrogenWavefunction", "ResourceFunctionLabel",
FontFamily->"Source Sans Pro"], " "}],
ShowAutoStyles->False,
ShowStringCharacters->False,
FontSize->Rational[12, 13] Inherited,
FontColor->GrayLevel[0.1]]}
},
GridBoxSpacings->{"Columns" -> {{0.25}}}],
Alignment->Left,
BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False},
BaselinePosition->Baseline,
FrameMargins->{{3, 0}, {0, 0}}],
ItemBox[
PaneBox[
TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource[
"FEBitmaps", "IconizeCloser"]], False-> DynamicBox[FEPrivate`FrontEndResource[
"FEBitmaps", "IconizeOpener"]]},
Appearance->None,
BaselinePosition->Baseline,
ContentPadding->False,
FrameMargins->0],
Alignment->Left,
BaselinePosition->Baseline,
FrameMargins->{{1, 1}, {0, 0}}],
Frame->{{
RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]}
},
BaselinePosition->{1, 1},
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}},
GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}]},
{
StyleBox[
PaneBox[GridBox[{
{
RowBox[{
TagBox["\<\"Version (latest): \"\>",
"IconizedLabel"], " ",
TagBox["\<\"1.0.0\"\>",
"IconizedItem"]}]},
{
TagBox[
TemplateBox[{"\"Documentation »\"", "https://resources.wolframcloud.com/FunctionRepository/resources/HydrogenWavefunction"},
"HyperlinkURL"],
"IconizedItem"]}
},
DefaultBaseStyle->"Column",
GridBoxAlignment->{"Columns" -> {{Left}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}],
Alignment->Left,
BaselinePosition->Baseline,
FrameMargins->{{5, 4}, {0, 4}}], "DialogStyle",
FontFamily->"Roboto",
FontSize->11]}
},
BaselinePosition->{1, 1},
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxDividers->{"Columns" -> {{None}}, "Rows" -> {False, {
GrayLevel[0.8]}, False}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}]}, Dynamic[Typeset`open],
BaselinePosition->Baseline,
ImageSize->Automatic],
Background->RGBColor[
0.9686274509803922, 0.9764705882352941, 0.984313725490196],
BaselinePosition->Baseline,
DefaultBaseStyle->{},
FrameMargins->{{0, 0}, {1, 0}},
FrameStyle->RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627],
RoundingRadius->4]],
{"FunctionResourceBox",
RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784],
"HydrogenWavefunction"},
TagBoxNote->"FunctionResourceBox"],
ResourceFunction["HydrogenWavefunction"],
BoxID -> "HydrogenWavefunction",
Selectable->False][{3, 2, 1}, a, {r, \[Theta], \[Phi]}]] \*
InterpretationBox[
TagBox[
DynamicModuleBox[{Typeset`open = False},
FrameBox[
PaneSelectorBox[{False->GridBox[{
{
PaneBox[GridBox[{
{
StyleBox[
StyleBox[
AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>",
BoxBaselineShift->-0.25,
BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon",
FontColor->RGBColor[
0.8745098039215686, 0.2784313725490196, 0.03137254901960784]],
ShowStringCharacters->False,
FontFamily->"Source Sans Pro Black",
FontSize->0.6538461538461539 Inherited,
FontWeight->"Heavy",
PrivateFontOptions->{"OperatorSubstitution"->False}],
StyleBox[
RowBox[{
StyleBox["HydrogenWavefunction", "ResourceFunctionLabel",
FontFamily->"Source Sans Pro"], " "}],
ShowAutoStyles->False,
ShowStringCharacters->False,
FontSize->Rational[12, 13] Inherited,
FontColor->GrayLevel[0.1]]}
},
GridBoxSpacings->{"Columns" -> {{0.25}}}],
Alignment->Left,
BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False},
BaselinePosition->Baseline,
FrameMargins->{{3, 0}, {0, 0}}],
ItemBox[
PaneBox[
TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource[
"FEBitmaps", "IconizeCloser"],
ImageSizeCache->{11., {1., 10.}}], False-> DynamicBox[FEPrivate`FrontEndResource[
"FEBitmaps", "IconizeOpener"],
ImageSizeCache->{11., {1., 10.}}]},
Appearance->None,
BaselinePosition->Baseline,
ContentPadding->False,
FrameMargins->0],
Alignment->Left,
BaselinePosition->Baseline,
FrameMargins->{{1, 1}, {0, 0}}],
Frame->{{
RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]}
},
BaselinePosition->{1, 1},
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}},
GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}], True->GridBox[{
{GridBox[{
{
PaneBox[GridBox[{
{
StyleBox[
StyleBox[
AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>",
BoxBaselineShift->-0.25,
BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon",
FontColor->RGBColor[
0.8745098039215686, 0.2784313725490196, 0.03137254901960784]],
ShowStringCharacters->False,
FontFamily->"Source Sans Pro Black",
FontSize->0.6538461538461539 Inherited,
FontWeight->"Heavy",
PrivateFontOptions->{"OperatorSubstitution"->False}],
StyleBox[
RowBox[{
StyleBox["HydrogenWavefunction", "ResourceFunctionLabel",
FontFamily->"Source Sans Pro"], " "}],
ShowAutoStyles->False,
ShowStringCharacters->False,
FontSize->Rational[12, 13] Inherited,
FontColor->GrayLevel[0.1]]}
},
GridBoxSpacings->{"Columns" -> {{0.25}}}],
Alignment->Left,
BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False},
BaselinePosition->Baseline,
FrameMargins->{{3, 0}, {0, 0}}],
ItemBox[
PaneBox[
TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource[
"FEBitmaps", "IconizeCloser"]], False-> DynamicBox[FEPrivate`FrontEndResource[
"FEBitmaps", "IconizeOpener"]]},
Appearance->None,
BaselinePosition->Baseline,
ContentPadding->False,
FrameMargins->0],
Alignment->Left,
BaselinePosition->Baseline,
FrameMargins->{{1, 1}, {0, 0}}],
Frame->{{
RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]}
},
BaselinePosition->{1, 1},
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}},
GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}]},
{
StyleBox[
PaneBox[GridBox[{
{
RowBox[{
TagBox["\<\"Version (latest): \"\>",
"IconizedLabel"], " ",
TagBox["\<\"1.0.0\"\>",
"IconizedItem"]}]},
{
TagBox[
TemplateBox[{"\"Documentation »\"", "https://resources.wolframcloud.com/FunctionRepository/resources/HydrogenWavefunction"},
"HyperlinkURL"],
"IconizedItem"]}
},
DefaultBaseStyle->"Column",
GridBoxAlignment->{"Columns" -> {{Left}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}],
Alignment->Left,
BaselinePosition->Baseline,
FrameMargins->{{5, 4}, {0, 4}}], "DialogStyle",
FontFamily->"Roboto",
FontSize->11]}
},
BaselinePosition->{1, 1},
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxDividers->{"Columns" -> {{None}}, "Rows" -> {False, {
GrayLevel[0.8]}, False}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}]}, Dynamic[Typeset`open],
BaselinePosition->Baseline,
ImageSize->Automatic],
Background->RGBColor[
0.9686274509803922, 0.9764705882352941, 0.984313725490196],
BaselinePosition->Baseline,
DefaultBaseStyle->{},
FrameMargins->{{0, 0}, {1, 0}},
FrameStyle->RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627],
RoundingRadius->4]],
{"FunctionResourceBox",
RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784],
"HydrogenWavefunction"},
TagBoxNote->"FunctionResourceBox"],
ResourceFunction["HydrogenWavefunction"],
BoxID -> "HydrogenWavefunction",
Selectable->False][{3, 2, \(-1\)}, a, {r, \[Theta], \[Phi]}]
\*SuperscriptBox[\(r\), \(2\)] Sin[\[Theta]] \[DifferentialD]r \[DifferentialD]\[Theta] \[DifferentialD]\[Phi]\)\)\)]](https://www.wolframcloud.com/obj/resourcesystem/images/ed5/ed55c685-e337-4ac2-8b57-e1ac163b5570/753ca337efff776f.png) |
| Out[6]= |  |
Verify the normalization property of HydrogenWavefunction:
| In[7]:= | ![Assuming[a > 0, \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(2 \[Pi]\)]\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(\[Pi]\)]\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(\[Infinity]\)]\*
SuperscriptBox[
RowBox[{"Abs", "[",
RowBox[{
InterpretationBox[
TagBox[
DynamicModuleBox[{Typeset`open = False},
FrameBox[
PaneSelectorBox[{False->GridBox[{
{
PaneBox[GridBox[{
{
StyleBox[
StyleBox[
AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>",
BoxBaselineShift->-0.25,
BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon",
FontColor->RGBColor[
0.8745098039215686, 0.2784313725490196, 0.03137254901960784]],
ShowStringCharacters->False,
FontFamily->"Source Sans Pro Black",
FontSize->0.6538461538461539 Inherited,
FontWeight->"Heavy",
PrivateFontOptions->{"OperatorSubstitution"->False}],
StyleBox[
RowBox[{
StyleBox["HydrogenWavefunction", "ResourceFunctionLabel",
FontFamily->"Source Sans Pro"], " "}],
ShowAutoStyles->False,
ShowStringCharacters->False,
FontSize->Rational[12, 13] Inherited,
FontColor->GrayLevel[0.1]]}
},
GridBoxSpacings->{"Columns" -> {{0.25}}}],
Alignment->Left,
BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False},
BaselinePosition->Baseline,
FrameMargins->{{3, 0}, {0, 0}}],
ItemBox[
PaneBox[
TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource[
"FEBitmaps", "IconizeCloser"],
ImageSizeCache->{11., {1., 10.}}], False-> DynamicBox[FEPrivate`FrontEndResource[
"FEBitmaps", "IconizeOpener"],
ImageSizeCache->{11., {1., 10.}}]},
Appearance->None,
BaselinePosition->Baseline,
ContentPadding->False,
FrameMargins->0],
Alignment->Left,
BaselinePosition->Baseline,
FrameMargins->{{1, 1}, {0, 0}}],
Frame->{{
RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]}
},
BaselinePosition->{1, 1},
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}},
GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}], True->GridBox[{
{GridBox[{
{
PaneBox[GridBox[{
{
StyleBox[
StyleBox[
AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>",
BoxBaselineShift->-0.25,
BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon",
FontColor->RGBColor[
0.8745098039215686, 0.2784313725490196, 0.03137254901960784]],
ShowStringCharacters->False,
FontFamily->"Source Sans Pro Black",
FontSize->0.6538461538461539 Inherited,
FontWeight->"Heavy",
PrivateFontOptions->{"OperatorSubstitution"->False}],
StyleBox[
RowBox[{
StyleBox["HydrogenWavefunction", "ResourceFunctionLabel",
FontFamily->"Source Sans Pro"], " "}],
ShowAutoStyles->False,
ShowStringCharacters->False,
FontSize->Rational[12, 13] Inherited,
FontColor->GrayLevel[0.1]]}
},
GridBoxSpacings->{"Columns" -> {{0.25}}}],
Alignment->Left,
BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False},
BaselinePosition->Baseline,
FrameMargins->{{3, 0}, {0, 0}}],
ItemBox[
PaneBox[
TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource[
"FEBitmaps", "IconizeCloser"]], False-> DynamicBox[FEPrivate`FrontEndResource[
"FEBitmaps", "IconizeOpener"]]},
Appearance->None,
BaselinePosition->Baseline,
ContentPadding->False,
FrameMargins->0],
Alignment->Left,
BaselinePosition->Baseline,
FrameMargins->{{1, 1}, {0, 0}}],
Frame->{{
RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]}
},
BaselinePosition->{1, 1},
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}},
GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}]},
{
StyleBox[
PaneBox[GridBox[{
{
RowBox[{
TagBox["\<\"Version (latest): \"\>",
"IconizedLabel"], " ",
TagBox["\<\"1.0.0\"\>",
"IconizedItem"]}]},
{
TagBox[
TemplateBox[{"\"Documentation »\"", "https://resources.wolframcloud.com/FunctionRepository/resources/HydrogenWavefunction"},
"HyperlinkURL"],
"IconizedItem"]}
},
DefaultBaseStyle->"Column",
GridBoxAlignment->{"Columns" -> {{Left}}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}],
Alignment->Left,
BaselinePosition->Baseline,
FrameMargins->{{5, 4}, {0, 4}}], "DialogStyle",
FontFamily->"Roboto",
FontSize->11]}
},
BaselinePosition->{1, 1},
GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}},
GridBoxDividers->{"Columns" -> {{None}}, "Rows" -> {False, {
GrayLevel[0.8]}, False}},
GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}]}, Dynamic[Typeset`open],
BaselinePosition->Baseline,
ImageSize->Automatic],
Background->RGBColor[
0.9686274509803922, 0.9764705882352941, 0.984313725490196],
BaselinePosition->Baseline,
DefaultBaseStyle->{},
FrameMargins->{{0, 0}, {1, 0}},
FrameStyle->RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627],
RoundingRadius->4]],
{"FunctionResourceBox",
RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784],
"HydrogenWavefunction"},
TagBoxNote->"FunctionResourceBox"],
ResourceFunction["HydrogenWavefunction"],
BoxID -> "HydrogenWavefunction",
Selectable->False], "[",
RowBox[{
RowBox[{"{",
RowBox[{"3", ",", "2", ",", "0"}], "}"}], ",", "a", ",",
RowBox[{"{",
RowBox[{"r", ",", "\[Theta]", ",", "\[Phi]"}], "}"}]}], "]"}], "]"}], "2"]
\*SuperscriptBox[\(r\), \(2\)] Sin[\[Theta]] \[DifferentialD]r \[DifferentialD]\[Theta] \[DifferentialD]\[Phi]\)\)\)]](https://www.wolframcloud.com/obj/resourcesystem/images/ed5/ed55c685-e337-4ac2-8b57-e1ac163b5570/338b5e95cc4b301a.png){kind=small} |
| Out[7]= |  |
Verify that HydrogenWavefunction satisfies the time-independent Schrödinger equation:
| In[8]:= | ![With[{n = 3, l = 2, m = -1},
\[Psi] = ResourceFunction["HydrogenWavefunction"][{n, l, m}, a, {r, \[Theta], \[Phi]}]; Simplify[-(\[HBar]^2/(2 \[Mu]))
Laplacian[\[Psi], {r, \[Theta], \[Phi]}, "Spherical"] - \[ScriptE]^2/(
4 \[Pi] Subscript[\[CurlyEpsilon], 0] r) \[Psi] == -(\[HBar]^2/(
2 \[Mu] a^2 n^2)) \[Psi] /. a -> (4 \[Pi] Subscript[\[CurlyEpsilon], 0] \[HBar]^2)/(\[Mu] \[ScriptE]^2)]]](https://www.wolframcloud.com/obj/resourcesystem/images/ed5/ed55c685-e337-4ac2-8b57-e1ac163b5570/0c0d8929cafa68ff.png) |
| Out[8]= |  |
Show a change of nuclear charge:
| In[9]:= | ![Grid[{#, ResourceFunction["HydrogenWavefunction"][{1, 0, 0}, a, {r, \[Theta], \[Phi]}, #]} & /@ {1, 2}, Frame -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/ed5/ed55c685-e337-4ac2-8b57-e1ac163b5570/202117182639d217.png){kind=small} |
| Out[9]= |  |
Neat Examples (1)
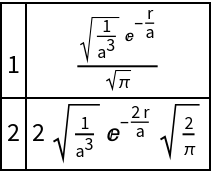Plot hydrogen orbital densities:
| In[10]:= | ![With[{a0 = Quantity["BohrRadius"]/Quantity["Meters"], n = 2, l = 1, m = 0}, DensityPlot3D[
Abs[ResourceFunction["HydrogenWavefunction"][{n, l, m}, a0, {Sqrt[x^2 + y^2 + z^2], ArcTan[z, Sqrt[x^2 + y^2]], ArcTan[x, y]}]]^2, {x, -5 a0, 5 a0}, {y, -5 a0, 5 a0}, {z, -5 a0,
5 a0}, PlotLegends -> Automatic]]](https://www.wolframcloud.com/obj/resourcesystem/images/ed5/ed55c685-e337-4ac2-8b57-e1ac163b5570/0ebf9e393e392fca.png) |
| Out[10]= |  |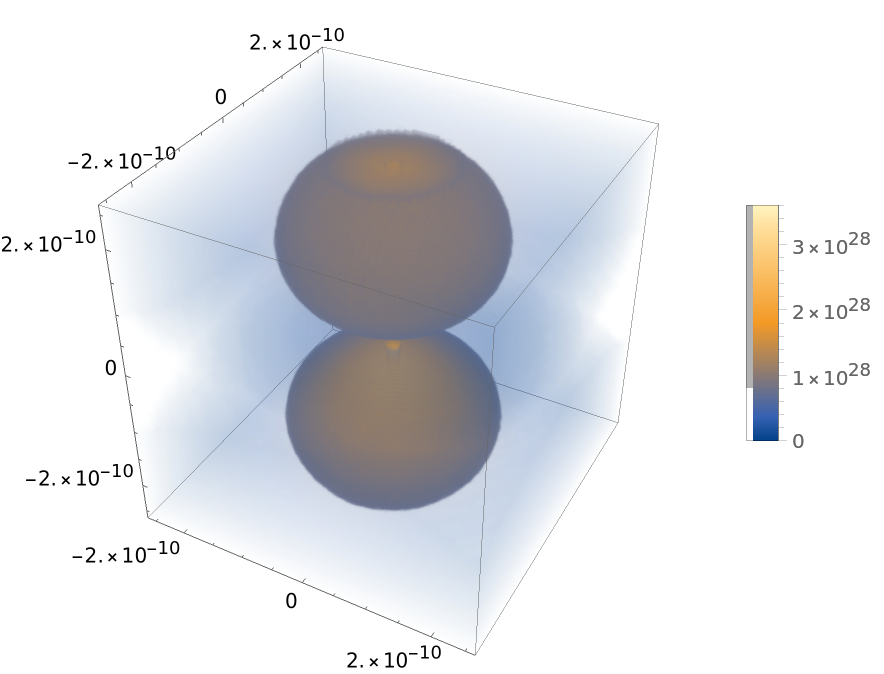
Publisher
Version History
- 1.0.0 – 07 June 2021
Source Metadata
Related Resources
Related Symbols
License Information
This work is licensed under a Creative Commons Attribution 4.0 International License