Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 HosoyaZ

Source Notebook

Compute the Hosoya Z index of a graph

Contributed by: Jan Mangaldan

ResourceFunction["HosoyaZ"][g]

computes the Hosoya index of the graph g.

Details

The Hosoya index is also known as the Z index.
The Hosoya index counts the total number of independent edge sets, or matchings, in an undirected graph.
ResourceFunction["HosoyaZ"][mol] computes the Hosoya index of a molecule mol, where the hydrogens are ignored by default. Use the option setting IncludeHydrogens→All to account for hydrogens.
ResourceFunction["HosoyaZ"][entity] computes the Hosoya index of an entity of type "Graph".

Examples

Basic Examples (2) 

The Hosoya index of a Petersen graph:

In[1]:=
ResourceFunction["HosoyaZ"][PetersenGraph[]]
Out[1]=

Get the same result from GraphData:

In[2]:=
GraphData["PetersenGraph", "HosoyaIndex"]
Out[2]=

Scope (2) 

Compute the Hosoya index of a molecule:

In[3]:=
ResourceFunction["HosoyaZ"][ Molecule[{"C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H"}, { Bond[{1, 2}, "Single"], Bond[{2, 3}, "Single"], Bond[{3, 4}, "Single"], Bond[{4, 5}, "Single"], Bond[{5, 6}, "Single"], Bond[{6, 7}, "Single"], Bond[{7, 8}, "Single"], Bond[{8, 9}, "Single"], Bond[{8, 10}, "Single"], Bond[{6, 1}, "Single"], Bond[{9, 2}, "Single"], Bond[{10, 4}, "Single"], Bond[{1, 11}, "Single"], Bond[{1, 12}, "Single"], Bond[{2, 13}, "Single"], Bond[{3, 14}, "Single"], Bond[{3, 15}, "Single"], Bond[{4, 16}, "Single"], Bond[{5, 17}, "Single"], Bond[{5, 18}, "Single"], Bond[{6, 19}, "Single"], Bond[{7, 20}, "Single"], Bond[{7, 21}, "Single"], Bond[{8, 22}, "Single"], Bond[{9, 23}, "Single"], Bond[{9, 24}, "Single"], Bond[{10, 25}, "Single"], Bond[{10, 26}, "Single"]}, {}]]
Out[3]=

Compute the Hosoya index of a named entity:

In[4]:=
ResourceFunction["HosoyaZ"][Entity["Graph", "UtilityGraph"]]
Out[4]=

Options (2) 

IncludeHydrogens (2) 

By default, hydrogens are ignored in the computation of the Hosoya index:

In[5]:=
ResourceFunction["HosoyaZ"][Molecule["neopentane"]]
Out[5]=

Use IncludeHydrogens→All to account for hydrogens:

In[6]:=
ResourceFunction["HosoyaZ"][Molecule["neopentane"], IncludeHydrogens -> All]
Out[6]=

Possible Issues (1) 

Computing the Hosoya index becomes slow even at a modest number of graph edges:

In[7]:=
Table[Timing[ResourceFunction["HosoyaZ"][CompleteGraph[j]]], {j, 8, 11}][[All, 1]]
Out[7]=
In[8]:=
ListLogPlot[%, DataRange -> {8, 11}, PlotRange -> All]
Out[8]=

Neat Examples (2) 

Generate the first few straight-chain alkanes:

In[9]:=
Array[Molecule@*ResourceFunction["AlkaneName"], 10]
Out[9]=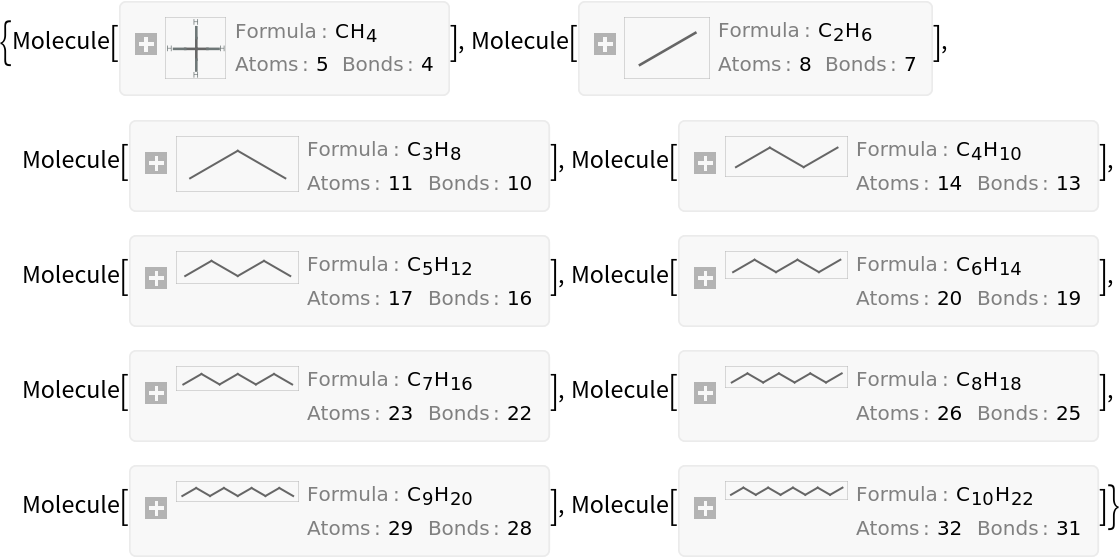

The Hosoya indices of the straight chain alkanes can be expressed as Fibonacci numbers:

In[10]:=
ResourceFunction["HosoyaZ"] /@ %
Out[10]=
In[11]:=
Array[Fibonacci, 10, 2]
Out[11]=

Generate the first few cycloalkanes:

In[12]:=
Array[Molecule["cyclo" <> ResourceFunction["AlkaneName"][#]] &, 10, 3]
Out[12]=

The Hosoya indices of the cycloalkanes can be expressed as Lucas numbers:

In[13]:=
ResourceFunction["HosoyaZ"] /@ %
Out[13]=
In[14]:=
Array[LucasL, 10, 3]
Out[14]=

Requirements

Wolfram Language 12.3 (May 2021) or above

Version History

  • 1.0.0 – 20 December 2023

Source Metadata

  • Citation:
    • Hosoya H. "Topological index. A newly proposed quantity characterizing the topological nature of structural isomers of saturated hydrocarbons." Bulletin of the Chemical Society of Japan, vol. 44, no. 9, 2332–2339, 1971.
      DOI: 10.1246/bcsj.44.2332
    • Hosoya H. "The Topological Index Z Before and After 1971." Internet Electronic Journal of Molecular Design, vol. 1, no. 9, 428–442, 2002.
      Available from       http://www.biochempress.com/av01_0428.html
    • Mihalić Z., Trinajstić N., "A graph-theoretical approach to structure-property relationships." Journal of Chemical Education, vol. 69, no. 9, 701–712, 1992.
      DOI: 10.1016/0009-2614(82)80009-2

Related Resources

Author Notes

HosoyaZ currently implements a general brute-force algorithm for generating matching counts. More efficient methods for special graphs will be implemented at a future date.

License Information