Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 HextileBins

Source Notebook

Bin data into hexagon tiles

Contributed by: Anton Antonov

ResourceFunction["HextileBins"][mat,r]

bins a numerical full 2D array mat into hexagon grid tiles with radius r.

ResourceFunction["HextileBins"][cv,r]

bins coordinates-to-value rules cv.

Details and Options

ResourceFunction["HextileBins"] bins data into hexagon tiles.
The result is an association with keys that are Polygon objects.
If the option "PolygonKeys" is set to False, then the keys of the result are hexagon centers.
The option "AggregationFunction" is used to aggregate the values within each tile.
"AggregationFunction"Totalfunction to aggegate the data in each tile
"PolygonKeys"Trueare the result keys polygons

Examples

Basic Examples (4) 

Create a list of random 2D points:

In[1]:=
SeedRandom[113]; data = RandomVariate[ MultinormalDistribution[{10, 10}, 7*IdentityMatrix[2]], 200];

Bin the points:

In[2]:=
ResourceFunction["HextileBins"][data, 10]
Out[2]=

Bin the points and get the hex-tile centers as keys:

In[3]:=
ResourceFunction["HextileBins"][data, 10, "PolygonKeys" -> False]
Out[3]=

Plot the points and the hexagon bins:

In[4]:=
Graphics[{EdgeForm[Black], FaceForm[Opacity[0.3]], Keys@ResourceFunction["HextileBins"][data, 10], Red, Point[data]}]
Out[4]=

Scope (4) 

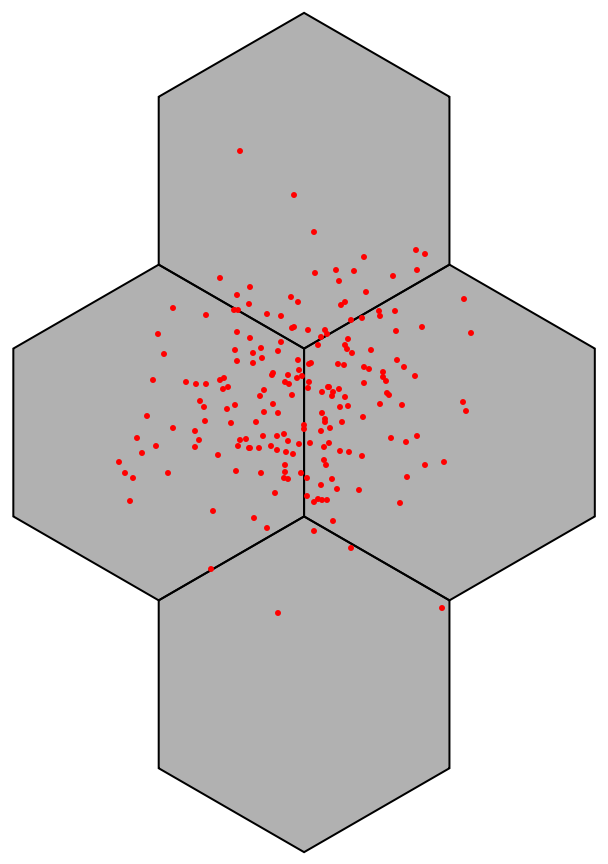Associate random values to 2D data:

In[5]:=
SeedRandom[113]; data = RandomVariate[ MultinormalDistribution[{10, 10}, 7*IdentityMatrix[2]], 200]; dataRules = AssociationThread[data, RandomReal[{0, 1}, Length[data]]];

Bin the data rules:

In[6]:=
ResourceFunction["HextileBins"][dataRules, 10]
Out[6]=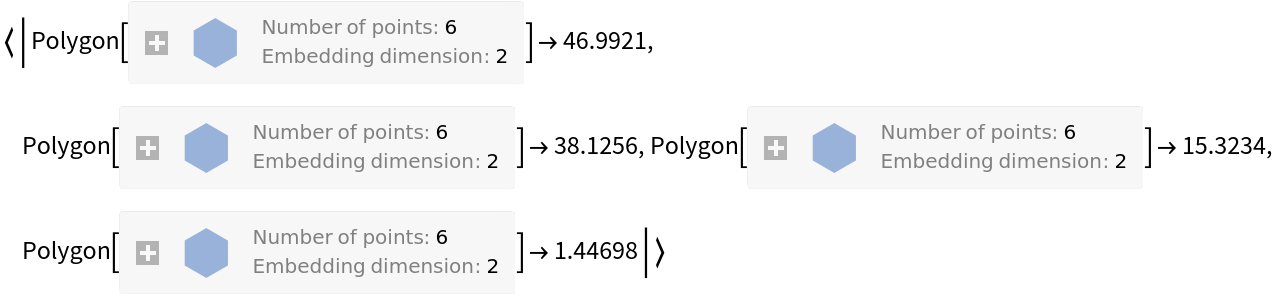

Bin the keys of the data rules:

In[7]:=
ResourceFunction["HextileBins"][Keys@dataRules, 10]
Out[7]=

Check the equivalence:

In[8]:=
ResourceFunction["HextileBins"][Keys@dataRules, 10] == ResourceFunction["HextileBins"][data, 10]
Out[8]=

Options (3) 

AggregationFunction (2) 

Bin the data rules and compute average values on each tile:

In[9]:=
SeedRandom[113]; data = RandomVariate[ MultinormalDistribution[{10, 10}, 7*IdentityMatrix[2]], 200]; dataRules = AssociationThread[data, RandomReal[{0, 1}, Length[data]]]; ResourceFunction["HextileBins"][dataRules, 6, "AggregationFunction" -> Mean]
Out[6]=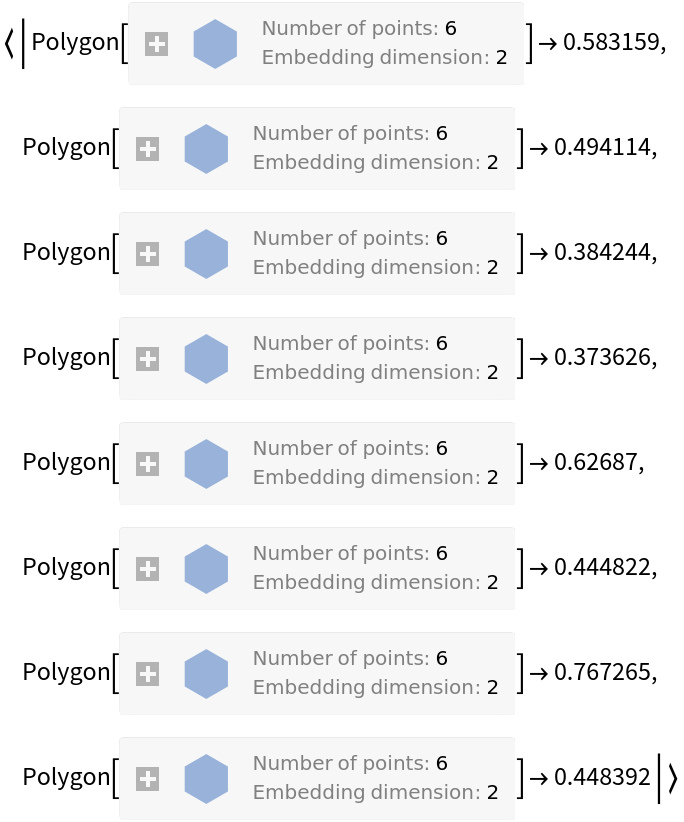

Compare with the default option value Total:

In[10]:=
ResourceFunction["HextileBins"][dataRules, 6, "AggregationFunction" -> Total]
Out[10]=

PolygonKeys (1) 

Instead of polygons as keys, you can get the centers of the polygons:

In[11]:=
SeedRandom[113]; data = RandomVariate[ MultinormalDistribution[{10, 10}, 7*IdentityMatrix[2]], 200]; dataRules = AssociationThread[data, RandomReal[{0, 1}, Length[data]]]; ResourceFunction[ "HextileBins"][dataRules, 10, "PolygonKeys" -> False]
Out[12]=

Applications (5) 

Data visualization (3) 

Generate data rules:

In[13]:=
SeedRandom[113]; data2 = RandomVariate[ MultinormalDistribution[{10, 10}, 7*IdentityMatrix[2]], 300]; dataRules2 = AssociationThread[data2, RandomReal[{0, 100}, Length[data2]]];

Here we bin the data:

In[14]:=
res2 = ResourceFunction["HextileBins"][dataRules2, 2];

Plot points and hexagon bins by coloring each hexagon according to its aggregated value:

In[15]:=
Graphics[{KeyValueMap[{FaceForm[ Opacity[Rescale[#2, MinMax[Values[res2]], {0, 1}], Blue]], #1} &, res2], Red, Point[Keys[dataRules2]]}, Frame -> True]
Out[15]=

Make a hexagonal grid (2) 

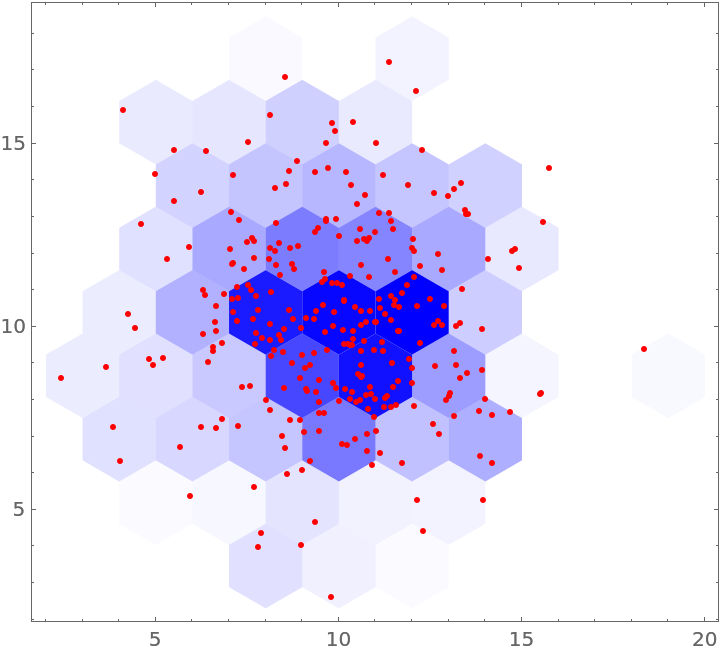You can make hexagonal grids:

In[16]:=
hexes = Keys@ ResourceFunction["HextileBins"][ Flatten[Table[{x, y}, {x, 0, 10}, {y, 0, 5}], 1], 2]; Graphics[{EdgeForm[Blue], FaceForm[None], hexes}]
Out[17]=

The coordinates of the polygons can be retrieved and transformed further:

In[18]:=
Mean@*PolygonCoordinates /@ hexes
Out[18]=

Properties and Relations (3) 

The function GeoHistogram produces similar plots (in Version 12.1):

In[19]:=
geoData = EntityValue[CountryData["Japan", "LargestCities"], "Position"];
In[20]:=
gr1 = GeoHistogram[geoData, GeoProjection -> "Equirectangular", Frame -> True, PlotLabel -> "GeoHistogram", ImageSize -> 250];
In[21]:=
geoRes = ResourceFunction["HextileBins"][Reverse[#[[1]]] & /@ geoData, 0.8]; gr2 = Graphics[{KeyValueMap[{FaceForm[ Blend[{Lighter[Lighter[Yellow]], Brown}, Rescale[#2, MinMax[Values[geoRes]], {0, 1}]]], #1} &, geoRes]}, Frame -> True, Prolog -> {LightBlue, Rectangle[Scaled[{0, 0}], Scaled[{1, 1}]]}, PlotLabel -> "HextileBins", ImageSize -> 250];
In[22]:=
Row[{gr1, Spacer[10], gr2}]
Out[22]=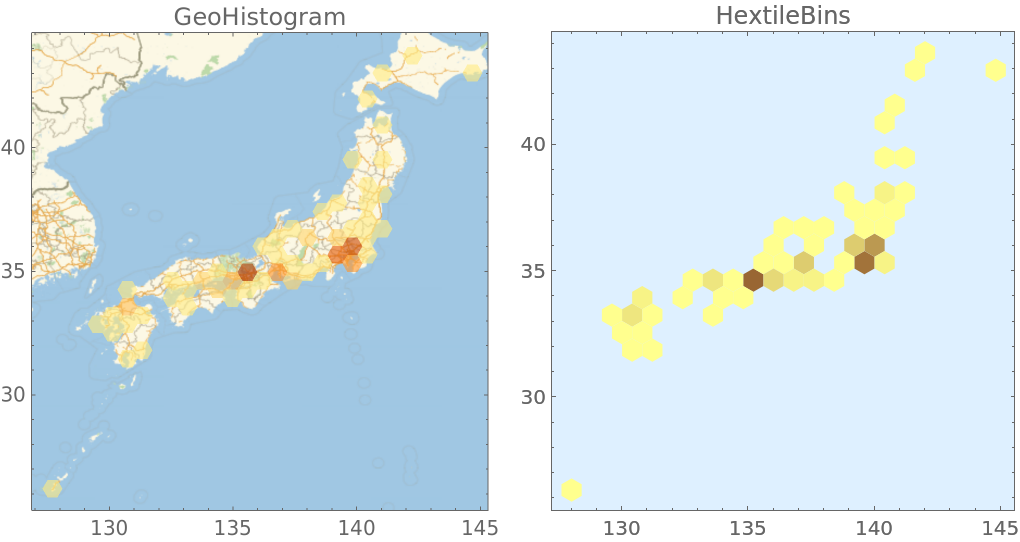

The resource function HexagonalGridGraph can be also used to make hexagonal grids:

In[23]:=
grHex = ResourceFunction["HexagonalGridGraph"][{4, 3}]
Out[23]=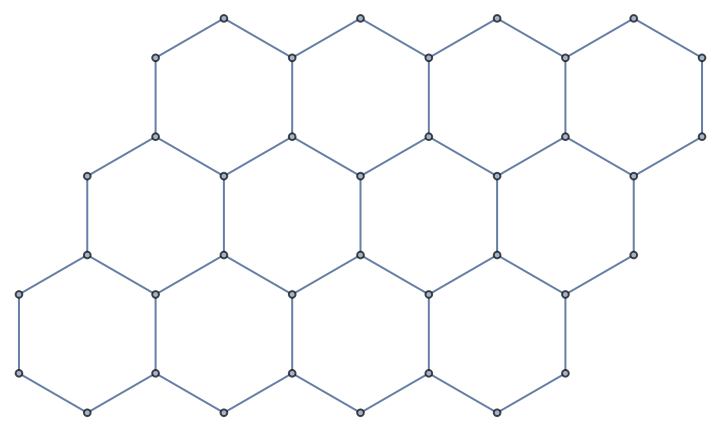

Here are the corresponding coordinates:

In[24]:=
lsVCoords = GraphEmbedding[grHex]
Out[24]=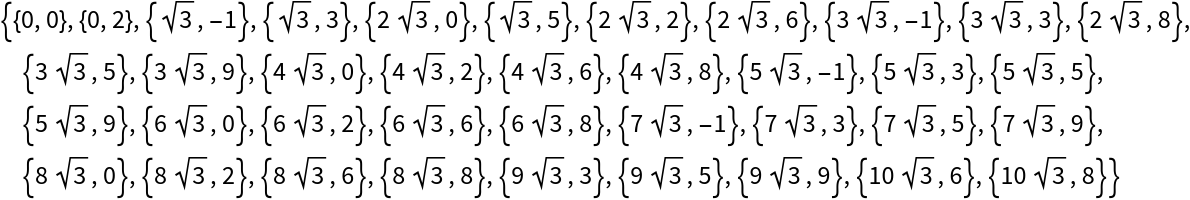

Here are the corresponding polygons:

In[25]:=
grHexPolygons = Map[Polygon@(List @@@ #)[[All, 1]] &, FindCycle[grHex, {6, 6}, All]] /. v_Integer :> lsVCoords[[v]]; Graphics[{EdgeForm[Blue], FaceForm[Opacity[0.2]], grHexPolygons}]
Out[15]=

Make a similar grid with HextileBins:

In[26]:=
hexes2 = Keys[ ResourceFunction["HextileBins"][ Flatten[Table[{x, y}, {x, 0, 6}, {y, 0, 3}], 1], 2]]; Graphics[{EdgeForm[Blue], FaceForm[Opacity[0.2]], hexes2}]
Out[27]=

Here are the corresponding coordinates:

In[28]:=
Union[Join @@ Map[PolygonCoordinates, hexes2]]
Out[28]=

The resource function TileBins has similar design and implementation as HextileBins. Here are comparable examples:

In[29]:=
GraphicsGrid[{{Graphics[{EdgeForm[Black], FaceForm[Opacity[0.3]], Keys@ResourceFunction["HextileBins"][data, 5], Red, Point[data]}, PlotLabel -> "HextileBins"], Graphics[{EdgeForm[Black], FaceForm[Opacity[0.3]], Keys@ResourceFunction["TileBins"][data, 5], Red, Point[data]}, PlotLabel -> "TileBins"]}}]
Out[29]=

Neat Examples (1) 

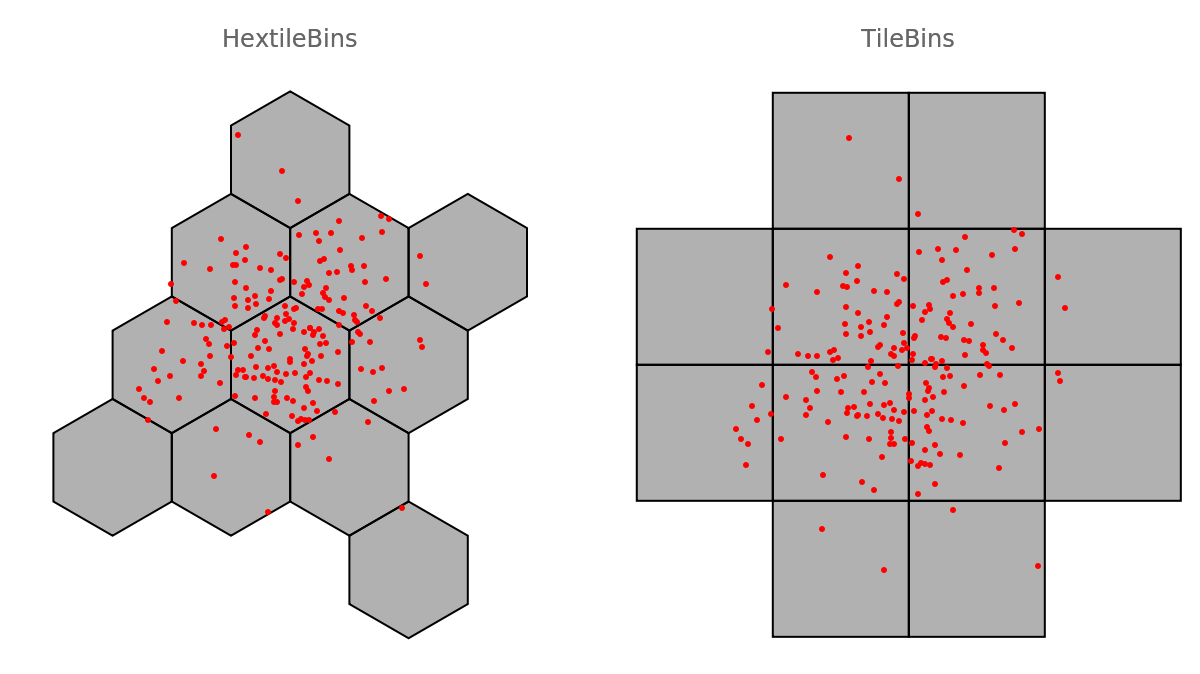Bin data and summarize the values associated with bin centers:

In[30]:=
SeedRandom[113]; data3 = RandomVariate[ MultinormalDistribution[{10, 10}, {1, 1.7}*IdentityMatrix[2]], 300]; dataRules3 = AssociationThread[data3, RandomReal[{0, 100}, Length[data3]]];
In[31]:=
res = ResourceFunction["HextileBins"][dataRules3, 10, "PolygonKeys" -> False, "AggregationFunction" -> ResourceFunction["RecordsSummary"]]
Out[31]=

Publisher

Anton Antonov

Version History

  • 2.0.0 – 11 November 2020
  • 1.0.0 – 08 April 2020

Related Resources

Author Notes

Initial ideas/versions of the code of HextileBins can be found in Mathematica Stack Exchange: https://mathematica.stackexchange.com/q/28149.

License Information