Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 HatHexagons

Source Notebook

Generate the hat tiling using combinatorial hexagons

Contributed by: Bradley Klee

ResourceFunction["HatHexagons"][ind]

plots the hexagonal initial condition for integer ind between 1 and 10.

ResourceFunction["HatHexagons"][ind, depth]

plots the resulting configuration of hexagons after applying the inflation rule an integer number of times, depth ≥ 0.

ResourceFunction["HatHexagons"][ind, depth, rotation]

rotates the resulting configuration by an angle rotation × π/3.

ResourceFunction["HatHexagons"][ind,…, type]

changes the view to show "Hat" or "Cluster" tiles instead of hexagons.

Details

The substitution rule presented here is essentially the same as presented in the original paper "An Aperiodic Monotile". However, from a details point-of-view, the substitution system is more like what is found in the sequel article "A chiral aperiodic monotile" (fig 5.1) which features nine combinatorial hexagons.
Of the three views—"Hexagon", "Hat", and "Cluster"—only "Hexagon" and "Cluster" can generate plane-filling configurations. The "Hat" view leaves holes where the reflected hats would be. This happens because reflected hats are essentially edge-like with regard to the inflation rule.
Although there are ten distinct "Hat" hexagons, there are only eight distinct "Cluster" hexagons. This fact can be found by analysis of HatTrialityTree outputs, or proven by combinatorial analysis of branching multiway growth sequences.
HatHexagons accepts three options, ColorFunction, ColorRules, and ImageSize. When ImageSize is set to Scaled[size], integer size directly affects the edge length of depicted polygons rather than the entire image height and width.

Examples

Basic Examples (3) 

Plot one of ten initial conditions as a hexagon:

In[1]:=
ResourceFunction["HatHexagons"][1]
Out[1]=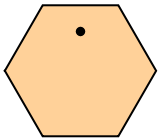

Compare different views of the same combinatorial hexagon:

In[2]:=
ResourceFunction["HatHexagons"][3, #] & /@ {"Hexagon", "Hat", "Cluster"}
Out[2]=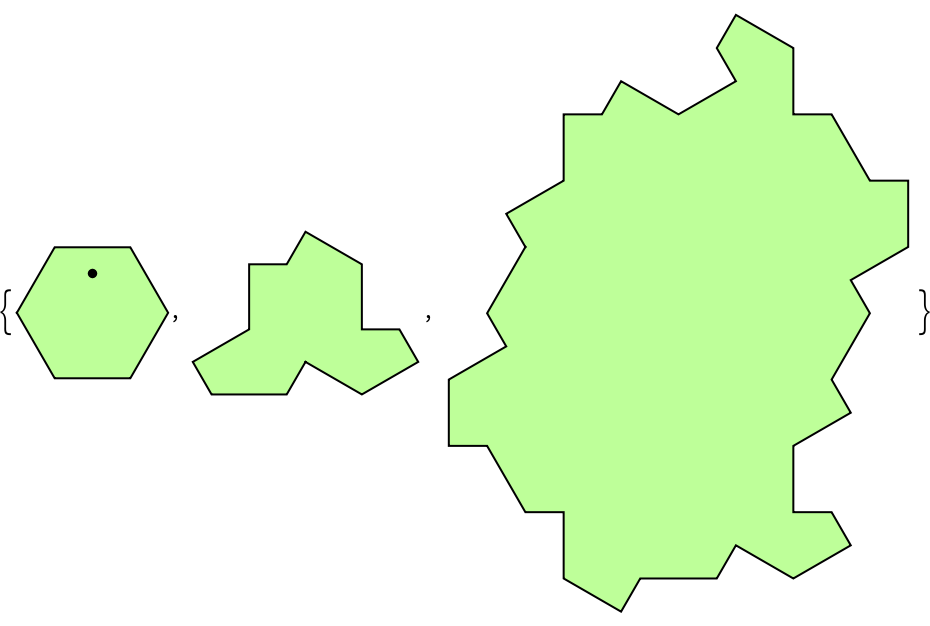

Obtain successively larger fragments of a hat-hexagon tiling:

In[3]:=
ResourceFunction["HatHexagons"][5, #, ImageSize -> Scaled[10]] & /@ Range[0, 2]
Out[3]=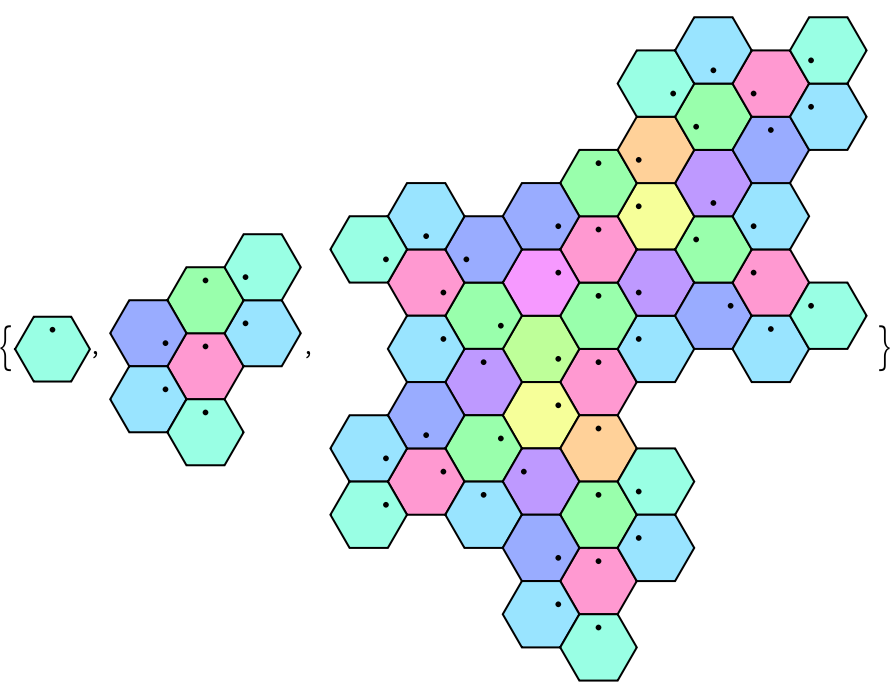

Compare with hat view:

In[4]:=
ResourceFunction["HatHexagons"][5, #, "Hat", ImageSize -> Scaled[10]] & /@ Range[0, 2]
Out[4]=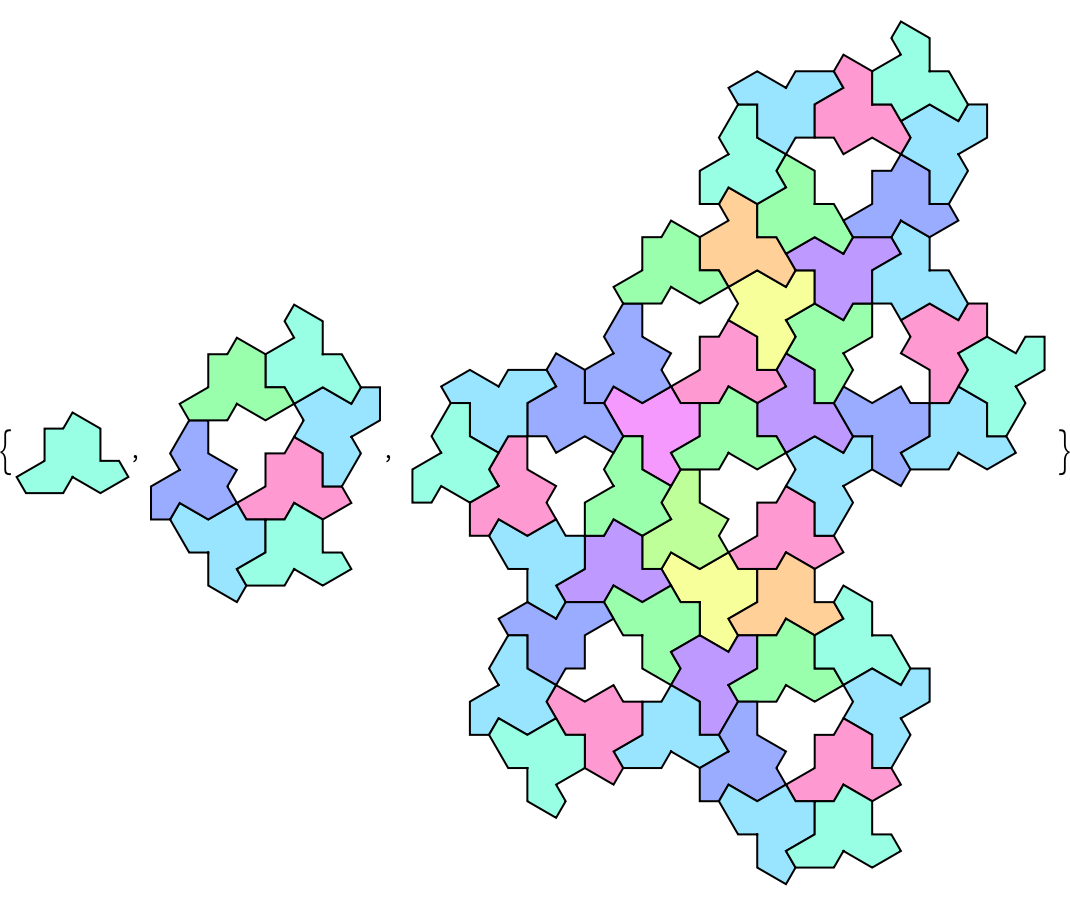

And compare with cluster view:

In[5]:=
ResourceFunction["HatHexagons"][5, #, "Cluster", ImageSize -> Scaled[3]] & /@ Range[0, 2]
Out[5]=

Scope (2) 

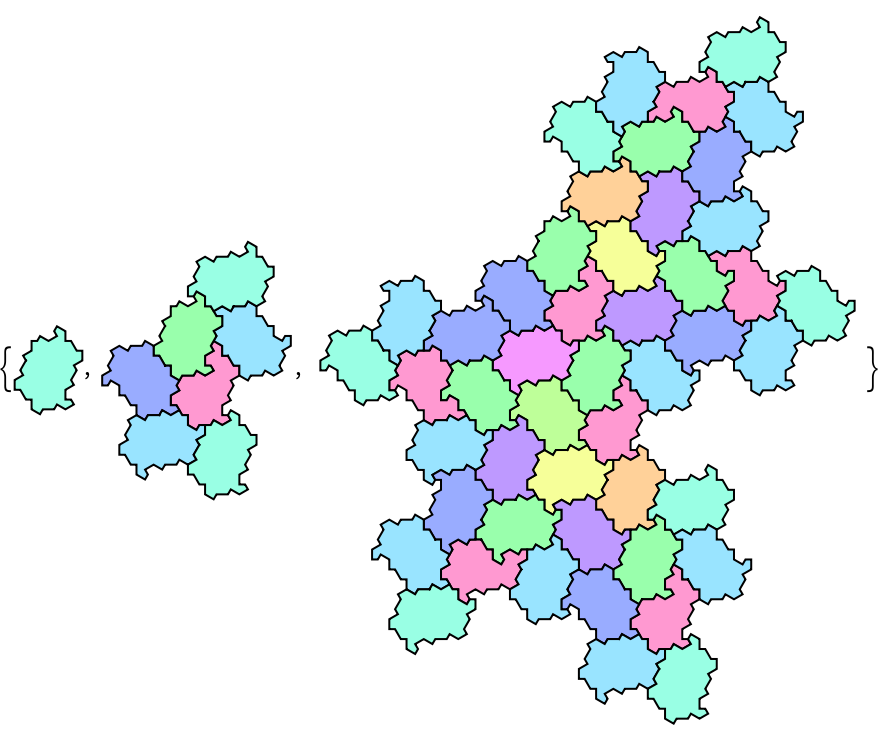Plot the ten initial conditions:

In[6]:=
Grid[Partition[ResourceFunction["HatHexagons"][#] & /@ Range[10], 5]]
Out[6]=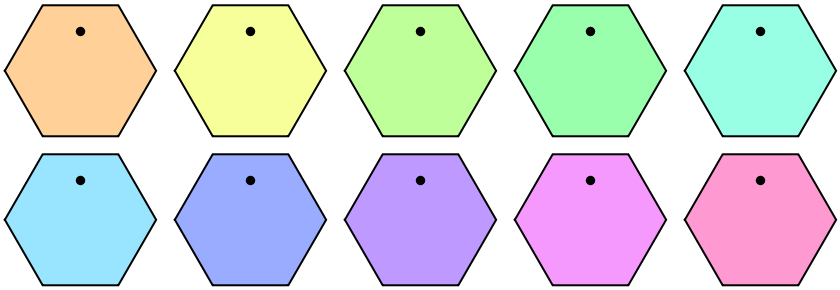

Their inflation images are not entirely unique:

In[7]:=
Grid[Partition[ ResourceFunction["HatHexagons"][#, 1, ImageSize -> 100] & /@ Range[10], 5]]
Out[7]=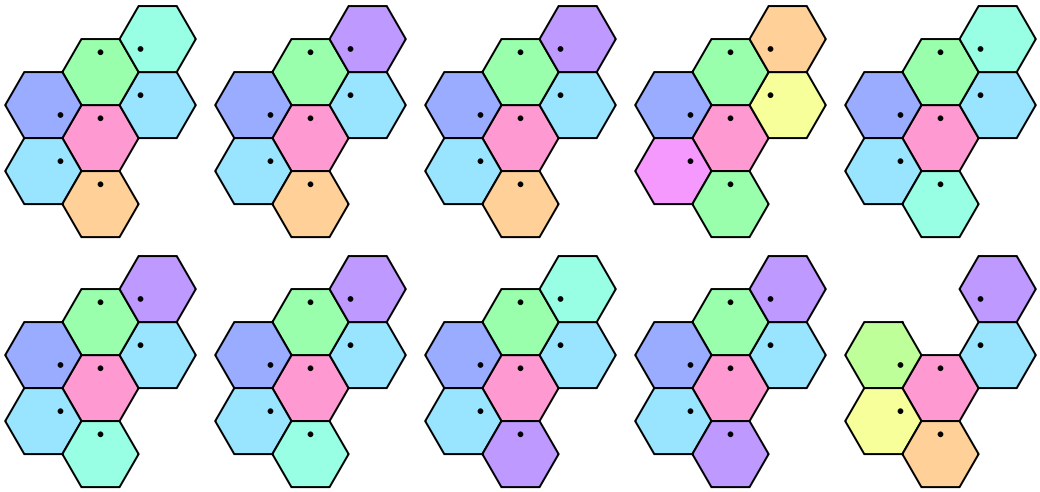

Each tile can be placed in six distinct orientations:

In[8]:=
ResourceFunction["HatHexagons"][10, 1, #, "Cluster", ImageSize -> Scaled[3]] & /@ Range[0, 5]
Out[8]=

Options (3) 

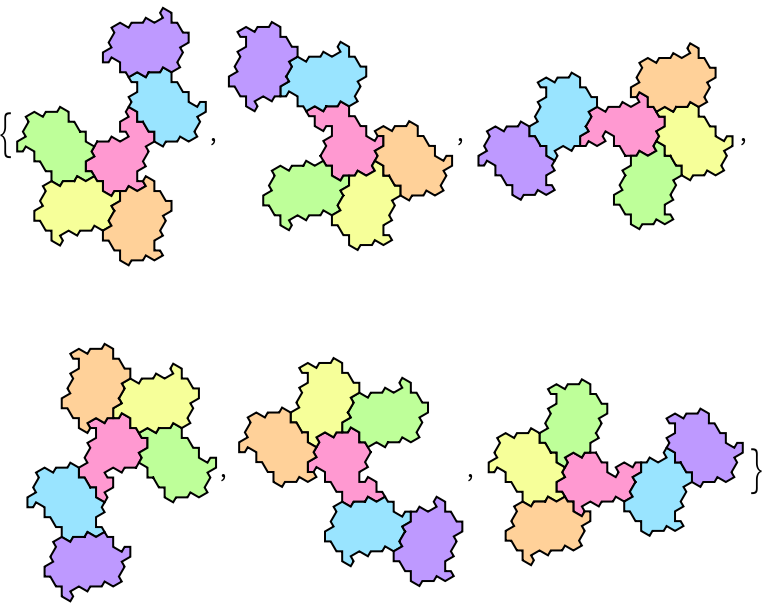Color the hat tiling using GrayLevel:

In[9]:=
ResourceFunction["HatHexagons"][1, 2, 2, "Hat", ColorRules -> ( x_ :> GrayLevel[x/12] ), ImageSize -> 500]
Out[9]=

Add red EdgeForm:

In[10]:=
ResourceFunction["HatHexagons"][1, 2, 2, "Hat", ColorRules -> ( x_ :> {EdgeForm[Darker[Red]], GrayLevel[x/12]} ), ImageSize -> 500]
Out[10]=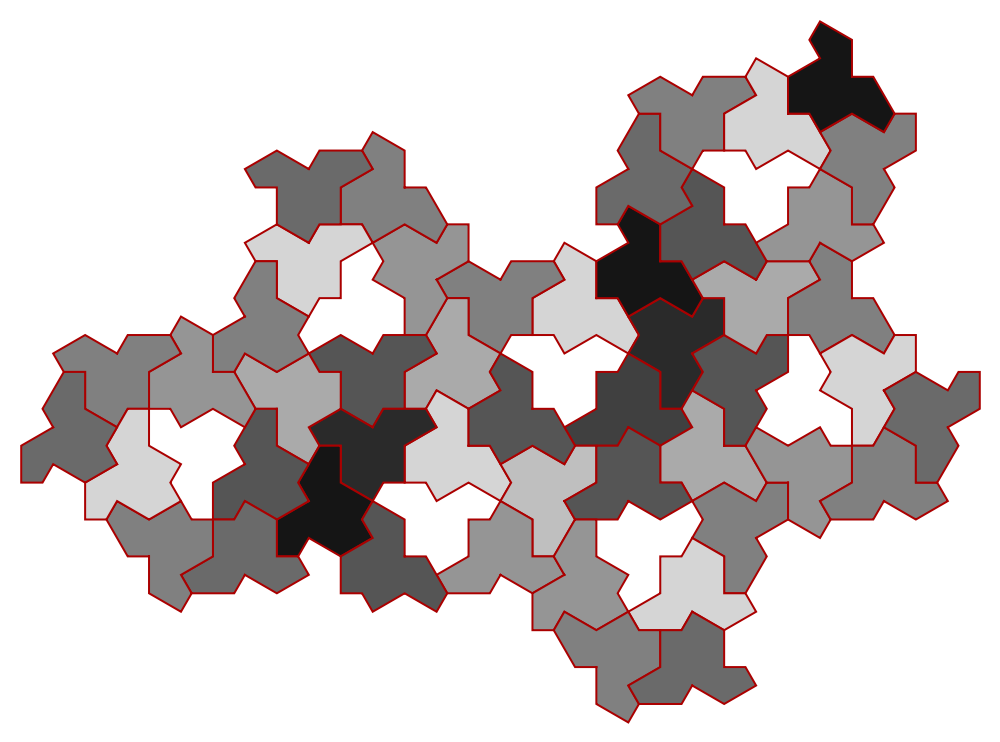

The same style can also be introduced using ColorFunction:

In[11]:=
ResourceFunction["HatHexagons"][1, 2, 2, "Hat", ColorFunction -> Function[ {EdgeForm[Darker[Red]], GrayLevel[#/12]}], ImageSize -> 500]
Out[11]=

Possible Issues (1) 

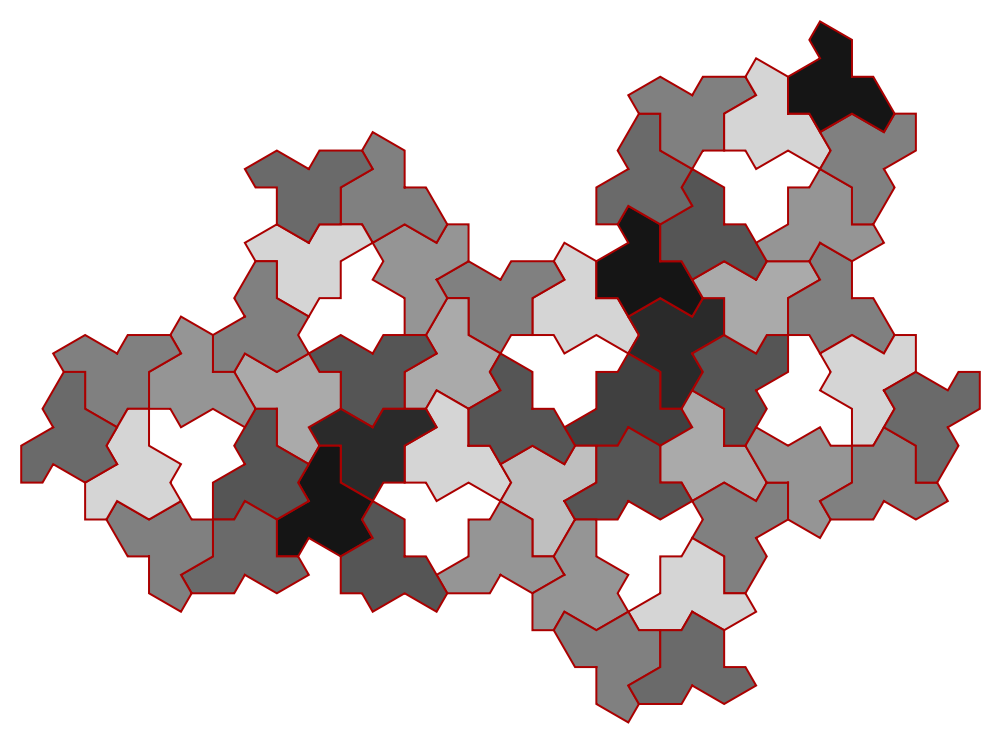Only three views are available:

In[12]:=
ResourceFunction["HatHexagons"][1, 1, "xx"]
Out[12]=

Neat Examples (1) 

Show a hexagon substitution:

In[13]:=
With[{ind = 6}, ResourceFunction["HatHexagons"][1, 4, 2, ColorFunction -> Function[ If[SameQ[#, ind], {EdgeForm[Gray], Gray}, {EdgeForm[Gray], White}]], ImageSize -> 600]]
Out[13]=

Publisher

Brad Klee

Version History

  • 1.0.0 – 22 September 2023

Source Metadata

Related Resources

License Information