Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 HatTrialityTree

Source Notebook

Generate trees describing the essential combinatorial structure of the aperiodic hat tiling

Contributed by: Bradley Klee

ResourceFunction["HatTrialityTree"][seed,n]

gives a tree grown from seed by n applications of the vertex replacement rules.

ResourceFunction["HatTrialityTree"][seed,n,m]

rotates the tree around its root by an angle of m × π/3.

Details

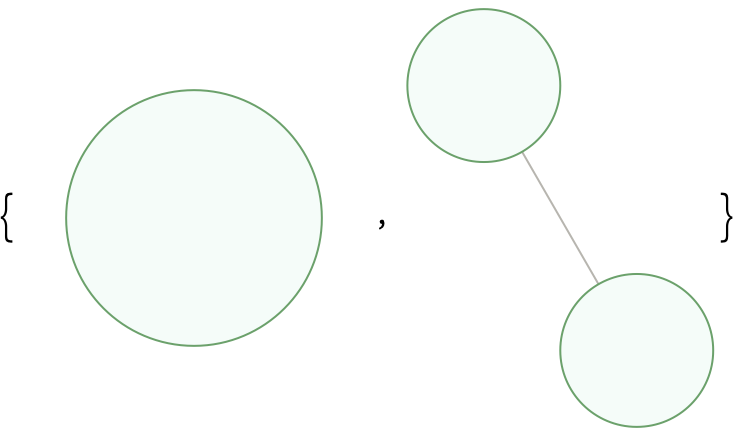
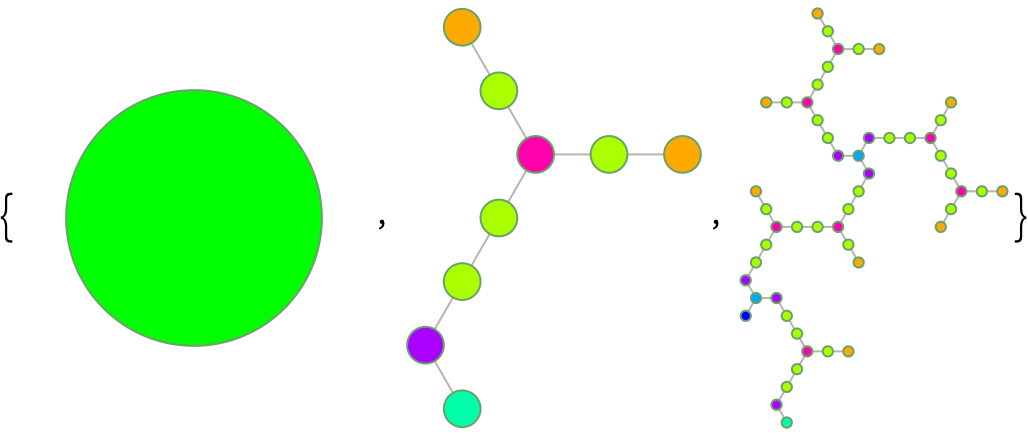
ResourceFunction["HatTrialityTree"] accepts all the options of Tree, and two additional options: ColorFunction and "Seeds". Any valid ColorFunction should accept up to two arguments: the first being a positive integer for vertex "Class", and the second being a bit (either a 0 or 1) describing the "Symmetry" type of the tree to which the vertex belongs. The "Seeds" option accepts a Boolean value, True or False, when set to True, causes ResourceFunction["HatTrialityTree"] to generate forests rather than isolated trees.
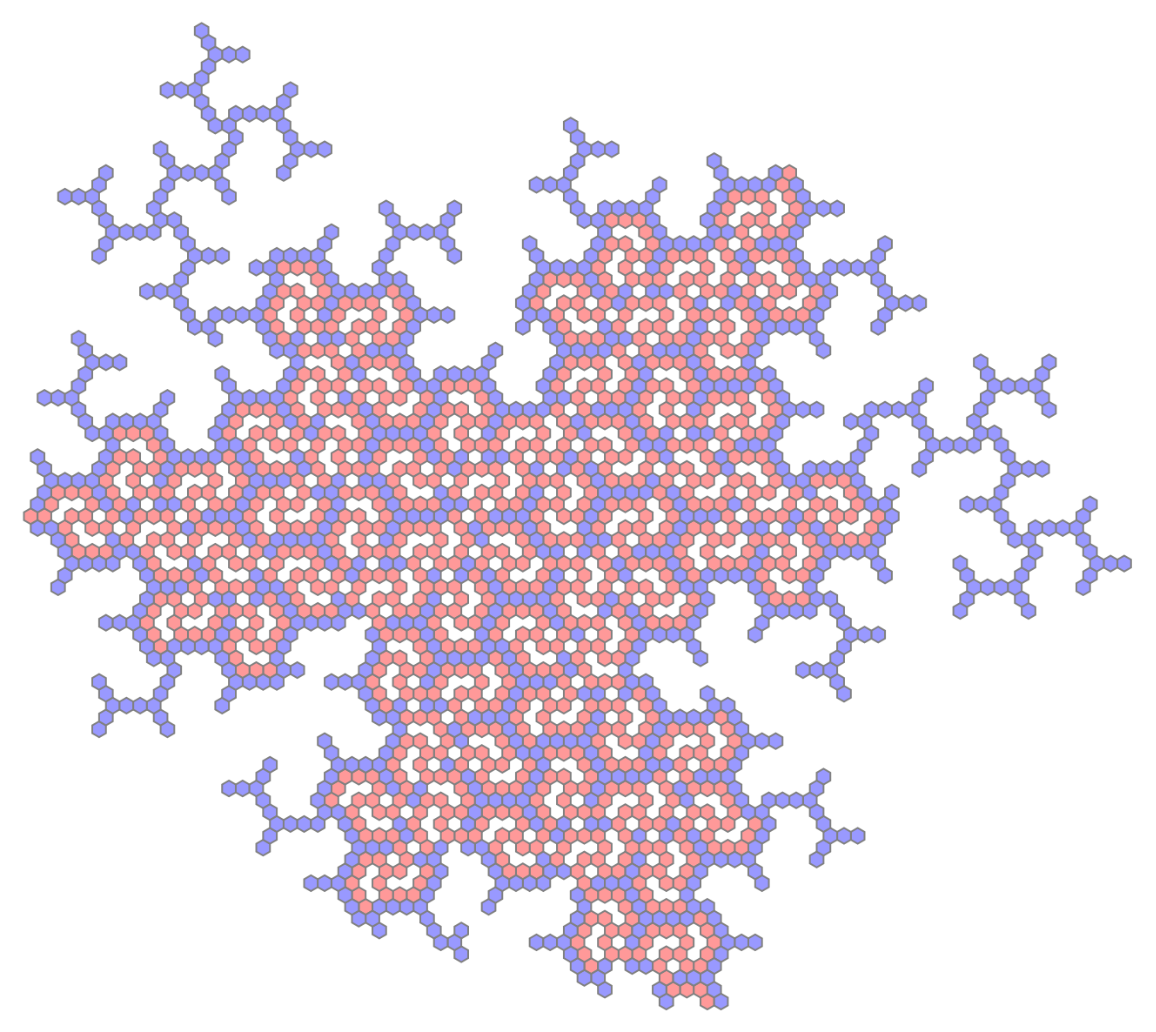
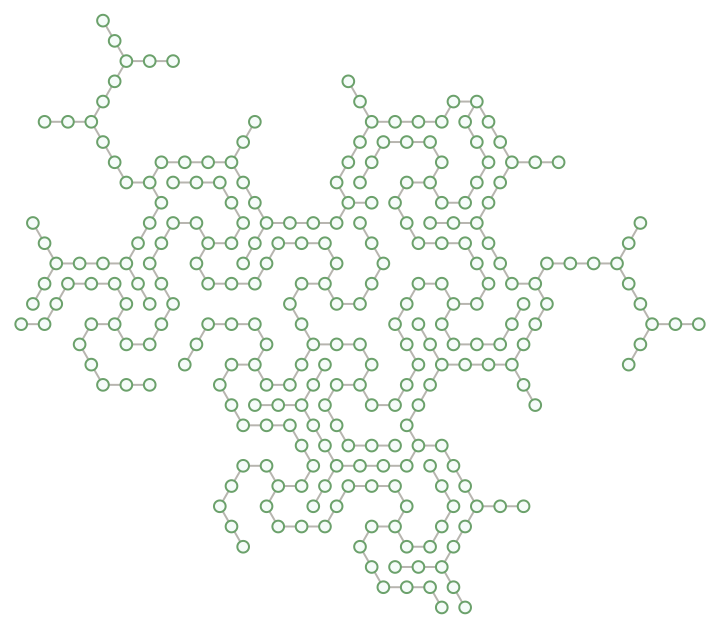
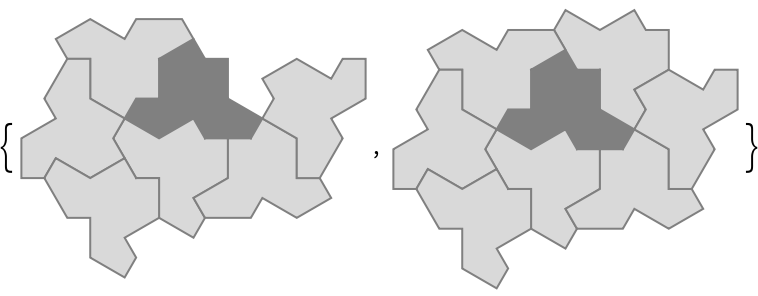
The "Hat triality pattern" is part of a new math discovery following from the groundbreaking research of David Smith et al. It is a three coloring of the hexagonal lattice, which describes valencies of some vertex figures in a Hat tiling.
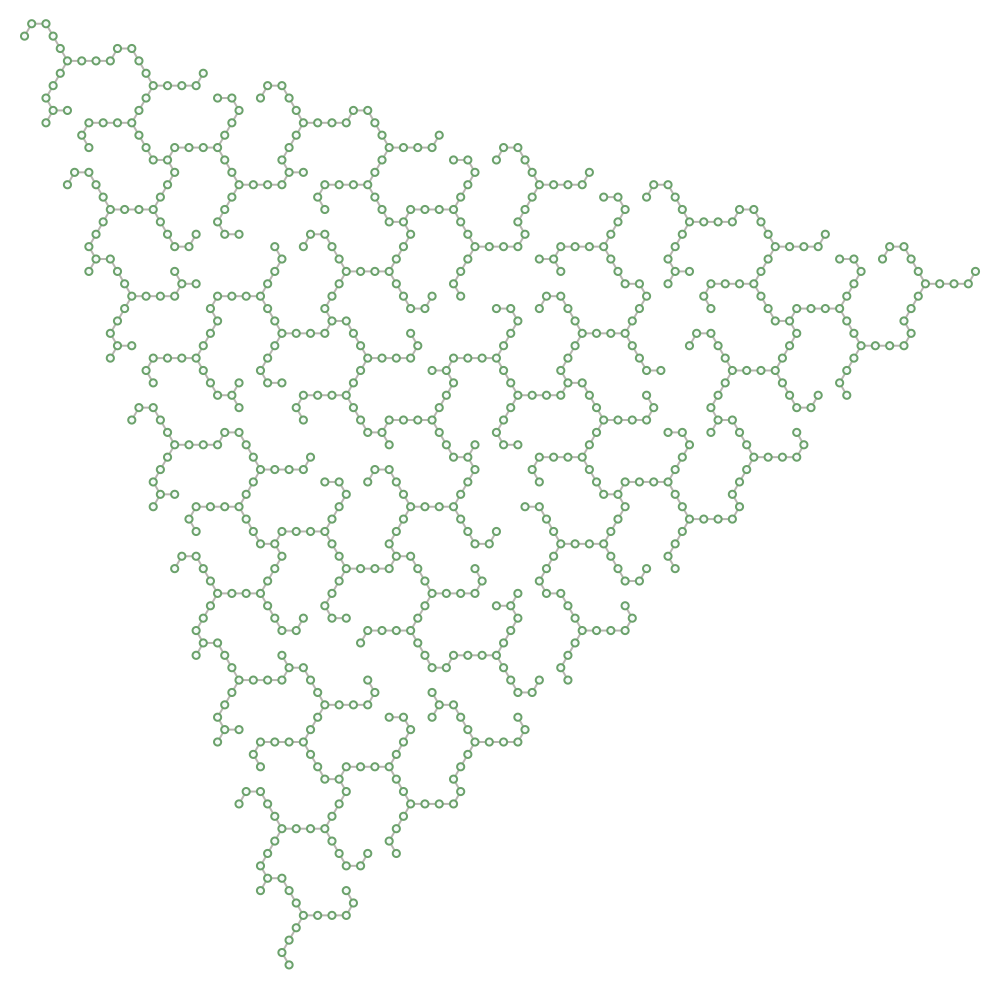
The Hat tiling is known to be aligned with the hexagonal lattice. The following map is used with lattice vertices at the center of each hexagon:

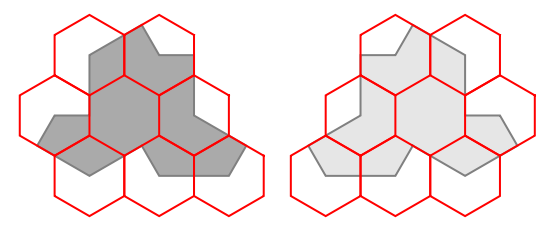
A duality pattern is obtained by classifying interior hexagons and edge-centered hexagons into two separate sets. A triality pattern is obtained from inner/outer duality by allowing edge-centered hexagons to fall into two distinct subsets. Subset membership depends upon how many Hat tiles are incident upon the corresponding lattice vertex, which can be either two or three.
The interior set must consist of isolated vertices so that edge 3-joins link with their neighbors to form ever-larger "triality trees". That is what has been discovered from analyzing large patches of the Hat tiling and the two-dimensional substitution rules that generate them.
The purpose of this function is not to recreate the valency triality pattern, but instead to recreate another more subtle triality pattern, the "mutual trees triality pattern" (see Neat Examples).
However, both "valence" and "mutual trees" triality patterns overlap on the set of edge 3-joins, which are called "the triality trees" or "the triality forest". These trees fall into two subsets. In ResourceFunction["HatTrialityTree"], the two subsets are generated by setting seed to 1 or 2. Unfortunately, any one triality tree is not plane-filling, so it cannot describe the entire Hat tiling.
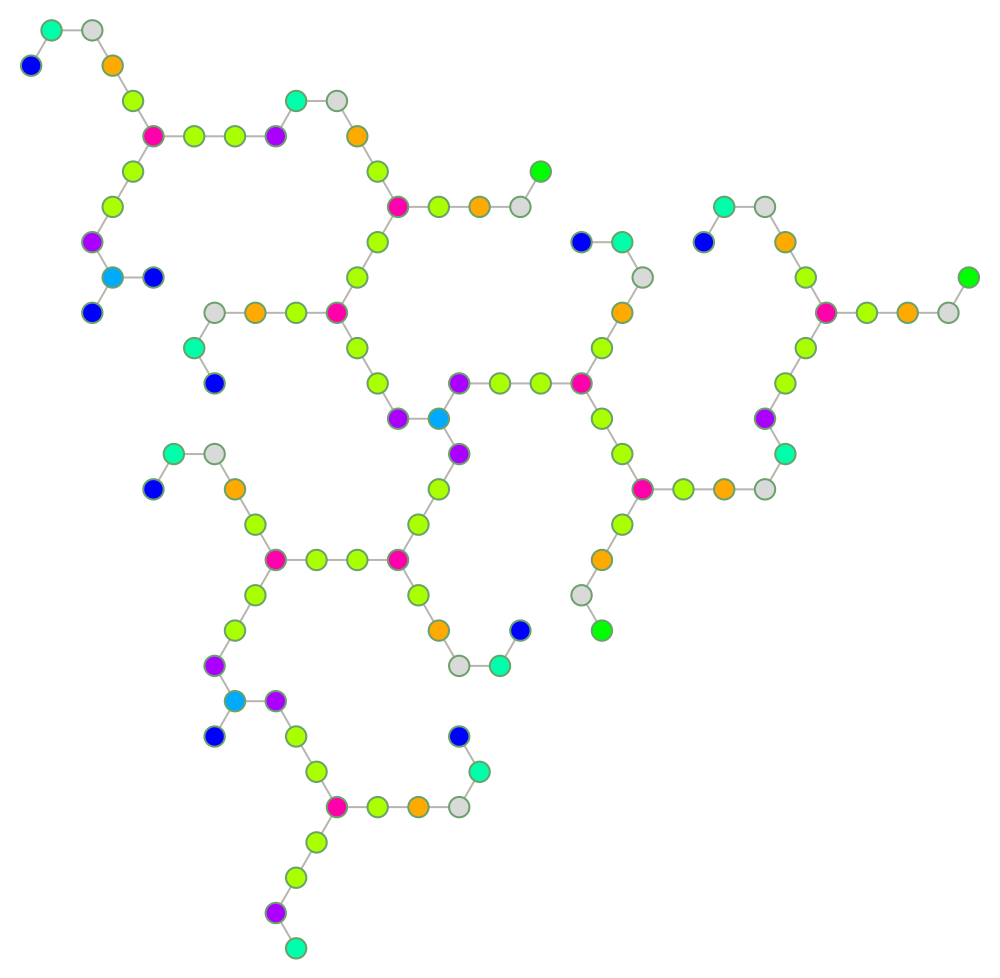
Closer analysis shows that the root vertices of smaller triality trees can be linked to branches of their older neighbors in a way that covers enough of the hexagonal lattice. When this is done correctly, by setting the option “Seeds”→True, the Hat tiling can be obtained by mapping H7 and H8 Hat clusters onto leaves of the triality tree (see Neat Examples).

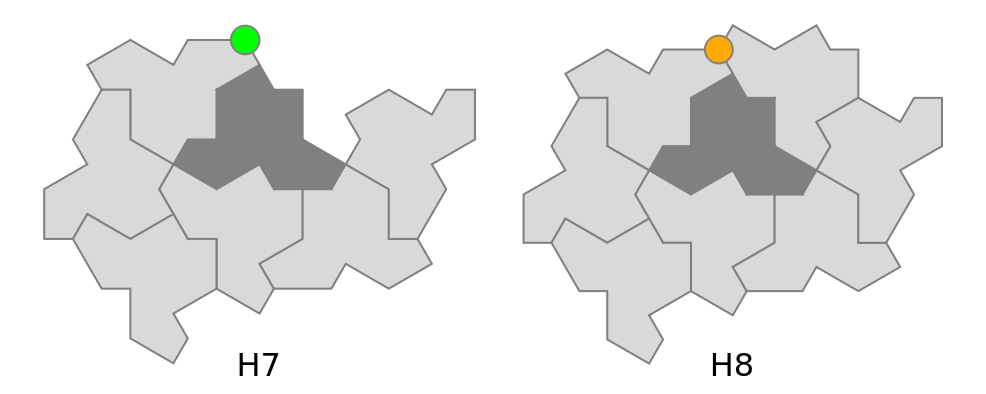
More precisely, reflected Hats at the center of the H7 and H8 clusters are in 1-to-1 correspondence with two particular types of 3-join vertices: proper terminals ("Class"=1 in this data model, Orange with ColorFunction→Hue), and singleton seeds ("Class”=3, Green). When clusters are drawn differently from the original paper (as above), the minority H7 can be put into 1-to-1 correspondence with singleton seeds.
By mixing some edge 2-joins with all interior vertices, a third tree can be obtained which covers about half the hexagonal lattice by itself, while still fitting in the interstices between isolated triality trees. By setting seed to 0, all types of symmetric trees are generated.
Setting seed to 3 joins symbols from the symmetric and asymmetric trees, resulting in a growth pattern that must collide on skip vertices ("Class”=0, LightGray). The resulting trees also only collide on skip vertices. This pattern intersperses symmetric and asymmetric triality trees, leaving a sparse third set of vacancies.

Examples

Basic Examples (4) 

The singleton and doubleton seeds:

In[1]:=
ResourceFunction["HatTrialityTree"][#] & /@ {1, 2}
Out[1]=

Grow the singleton seed through successive generations:

In[2]:=
ResourceFunction["HatTrialityTree"][1, #] & /@ Range[0, 2]
Out[2]=

Check the hidden data for the first larger singleton tree:

In[3]:=
TreeFold[Function[Flatten[Append[#2, #1]]], ResourceFunction["HatTrialityTree"][1, 1]] // Column
Out[3]=

Rotate a doubleton tree clockwise by π/3 radians:

In[4]:=
ResourceFunction["HatTrialityTree"][2, 1, -1]
Out[4]=

Scope (2) 

Another growth rule produces a symmetric tree:

In[5]:=
ResourceFunction["HatTrialityTree"][0, #] & /@ Range[3]
Out[5]=

A fourth seed combines symbols from both growth rules:

In[6]:=
ResourceFunction["HatTrialityTree"][3, 0]
Out[6]=

The growth rules are mutually consistent, and distinct trees do not collide without re-seeding:

In[7]:=
ResourceFunction["HatTrialityTree"][3, 2]
Out[7]=

Options (5) 

Color singleton trees according to vertex class:

In[8]:=
ResourceFunction["HatTrialityTree"][1, #, ColorFunction -> Hue] & /@ Range[0, 2]
Out[8]=

Fill space by allowing trees to re-seed their surroundings each generation:

In[9]:=
ResourceFunction["HatTrialityTree"][1, 2, "Seeds" -> True, ColorFunction -> Hue, ImageSize -> 500]
Out[9]=

Generate a larger patch of the triality forest:

In[10]:=
ResourceFunction["HatTrialityTree"][1, 3, "Seeds" -> True, ImageSize -> 500]
Out[10]=

Color the symmetric tree according to vertex class:

In[11]:=
ResourceFunction["HatTrialityTree"][0, 4, ColorFunction -> Function[ Association[1 -> Green, 2 -> Darker@Green, 3 -> Lighter[Red, .6], 4 -> White, 5 -> Lighter[Gray, .6], 6 -> Lighter[Blue, .6] ][#]], ImageSize -> 500]
Out[11]=

Color symmetric and asymmetric trees differently:

In[12]:=
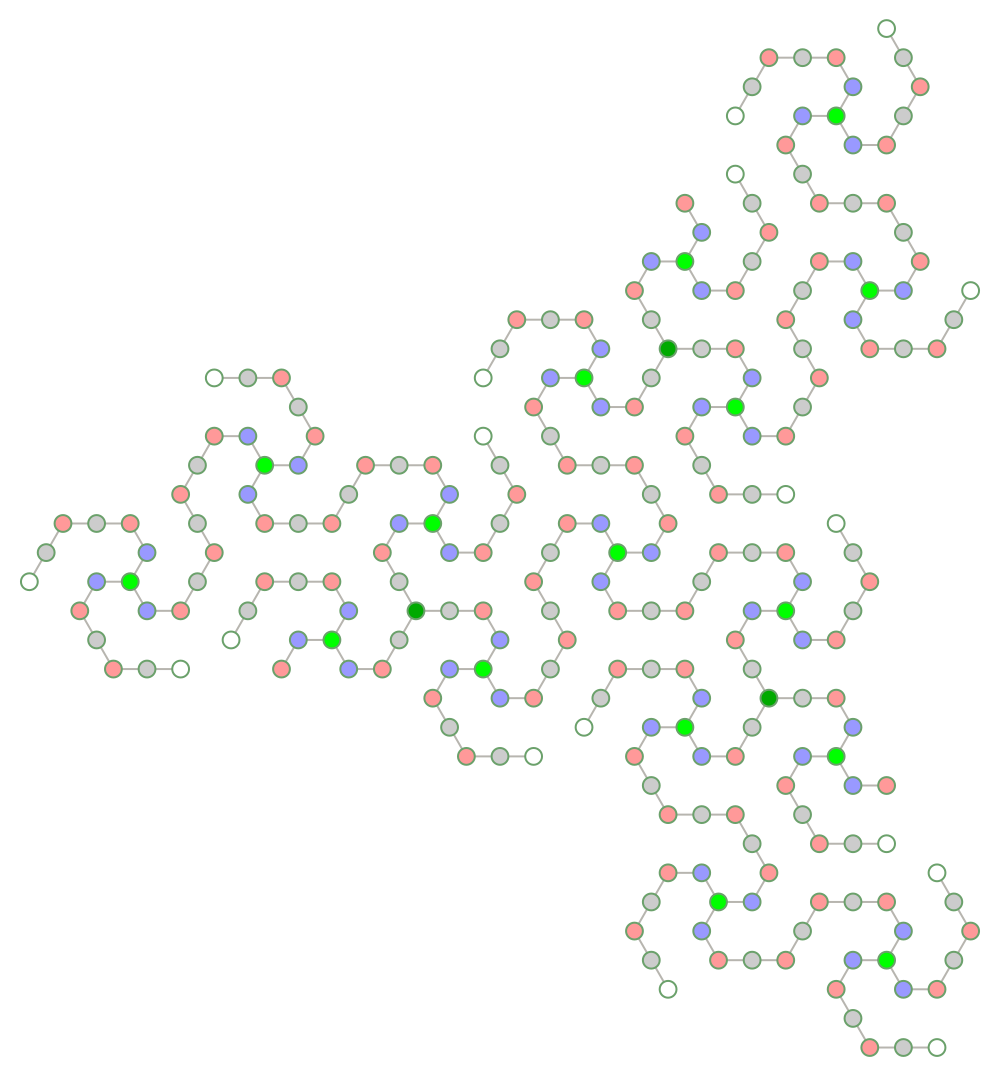
ResourceFunction["HatTrialityTree"][3, 2, 3, ColorFunction -> Function[Association[ 1 -> Lighter[Blue, .6], 0 -> Lighter[Red, .6] ][#2]], ImageSize -> 500]
Out[12]=

Properties and Relations (2) 

Count the number of class 8 vertices per generation:

In[13]:=
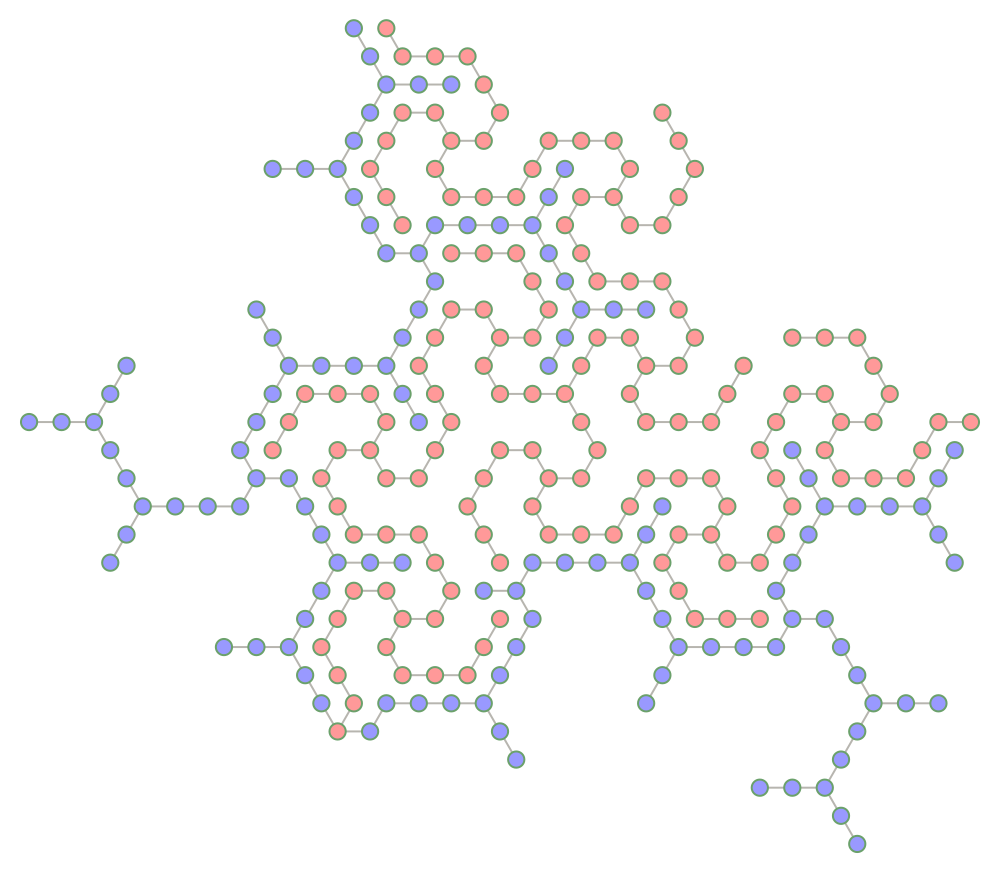
Count[TreeFold[Function[Flatten[Append[#2, #1["Class"]]]], ResourceFunction["HatTrialityTree"][1, #, "Seeds" -> True]], 8] & /@ Range[4]
Out[13]=

These are the squares of the Fibonacci numbers:

In[14]:=
Fibonacci[2 #]^2 & /@ Range[4]
Out[14]=

Calculate a weighted ratio from counts of class 1 and class 3 vertices:

In[15]:=
With[{counts = Counts[TreeFold[Function[Flatten[Append[#2, #1["Class"]]]], ResourceFunction["HatTrialityTree"][1, #, "Seeds" -> True]]] & /@ Range[4]}, Divide[7 #[1] + 6 #[3], #[1] + #[3]] & /@ counts ]
Out[15]=

Convert to decimal notation:

In[16]:=
N[%]
Out[16]=

Compare with the fourth power of the GoldenRatio:

In[17]:=
N[GoldenRatio^4]
Out[17]=

Possible Issues (2) 

With re-seeding, vertex collisions can affect graphical output:

In[18]:=
ResourceFunction["HatTrialityTree"][3, 1, 3, "Seeds" -> True]
Out[18]=

The data can still be used to extract patches of the mutual trees triality pattern:

In[19]:=
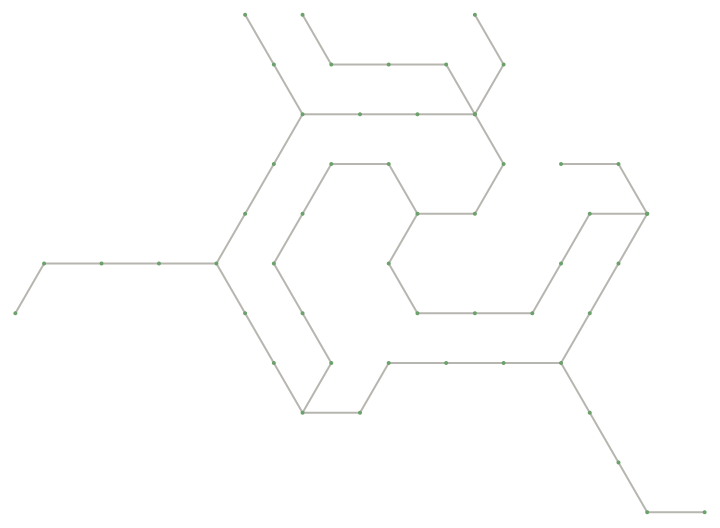
Graphics[{EdgeForm[Gray], Map[If[#["Class"] == 0, Nothing, {If[#["Symmetry"], Lighter[Red, .6], Lighter[Blue, .6]], Polygon[CirclePoints[#["Coordinates"], {2/Sqrt[3], Pi/6}, 6]]} ] &, TreeFold[Function[Flatten[Append[#2, #1]]], ResourceFunction["HatTrialityTree"][3, 1, 3, "Seeds" -> True]]]}]
Out[19]=

Neat Examples (2) 

Draw the "ein stein" Hat tile in either of two reflections:

In[20]:=
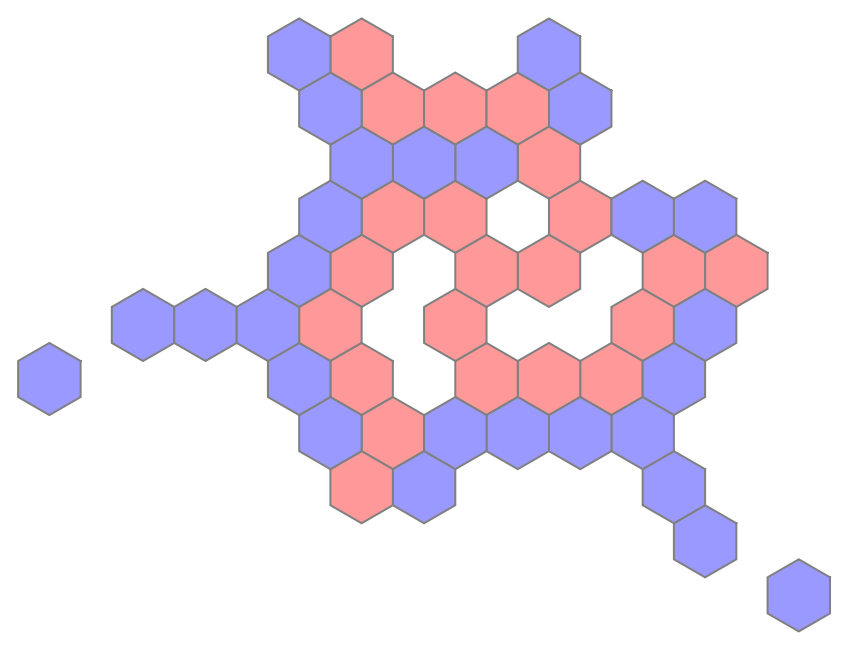
TilePolygon[ or_, dir_, ref_ : False, pt_ : 0 ] := Module[{edges, par = 1 - 2 Boole[ref], vecs}, edges = MapThread[{Sqrt[#1], Mod[par*(dir + #2), 12]} &, {{3, 3, 1, 1, 3, 3, 1, 1, 3, 3, 1, 4, 1}, {-1, 1, 4, 6, 3, 5, 8, 6, 9, 7, 10, 12, 14}}]; edges = RotateLeft[edges, pt]; edges = If[TrueQ[ref], Reverse[edges], edges]; vecs = MapApply[ Times[#1, ReIm[Exp[I Pi/6 #2]]] &, edges]; Polygon[Most[FoldList[Plus, or, vecs]]]]
In[21]:=
MapThread[Graphics[{#1, EdgeForm[Gray], TilePolygon[{0, 0}, 0, #2, 0]}] &, {{Gray, LightGray}, {True, False}}]
Out[21]=

Add surrounding tiles in either of two distinct ways:

In[22]:=
CoronaPolygons[ or_, dir_, drop_, pt_ : 0 ] := Module[{central, vertices, polygons}, central = TilePolygon[or, dir, True, pt]; vertices = Association[MapThread[Rule, { Reverse[RotateLeft[Mod[Range[13], 13], pt]], First[central]}]]; polygons = MapThread[ TilePolygon[#1, #2, False, #3] &, {Lookup[vertices, {12, 11, 8, 5, 10, 2}], {-dir - 2, -dir + 0, -dir - 2, -dir + 6, -dir + 2, -dir + 8}, {7, 7, 0, 9, 8, 8}}]; AppendTo[polygons, TilePolygon[polygons[[1, 1, 6]], -dir - 2, False, 7]]; If[TrueQ[drop], polygons[[{1, 2, 4, 5, 6, 7}]], polygons] ]
In[23]:=
Graphics[{Gray, EdgeForm[Gray], TilePolygon[{0, 0}, 0, True, 0], LightGray, CoronaPolygons[{0, 0}, 0, #, 0]}] & /@ {True, False}
Out[23]=

Use triality trees to draw larger and larger patches of the tiling:

In[24]:=
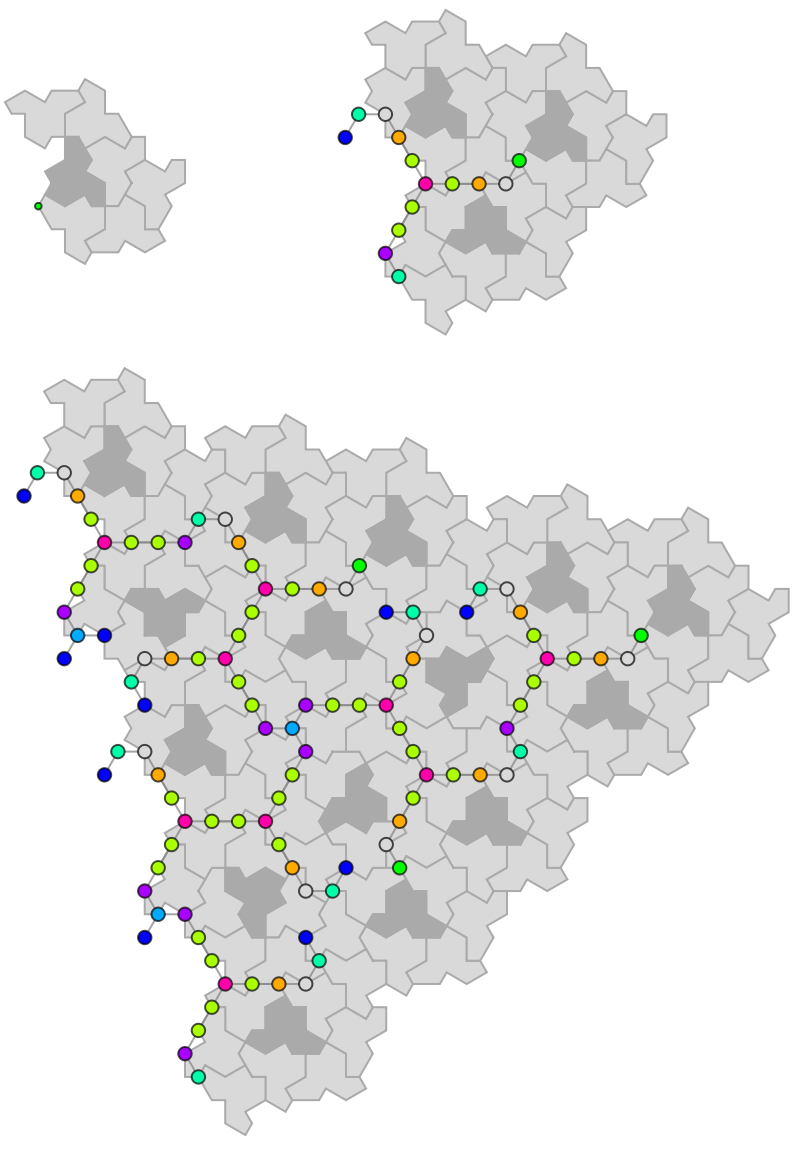
HatLeafUnderlay[tree_] := Module[ {terms, args, g0 = TreeGraph[tree]}, terms = TreeFold[Function[Flatten[Append[#2, If[MemberQ[{1, 3}, #1["Class"]], #1, {}] ]]], tree]; args = Transpose[Map[ {#["Coordinates"], Plus[First[#["OutDirections"]], If[#["Class"] == 1, -1, 5]], If[#["Class"] == 1, False, True] } &, terms]]; Show[#, ImageSize -> ( -7 Subtract @@@ (PlotRange /. AbsoluteOptions[#])) ] &@Show[Graphics[MapThread[{ EdgeForm[Lighter@Gray], LightGray, CoronaPolygons[#1 + ReIm[2 Exp[I Pi/3 #2]], 2 (-#2 + 5), #3, 7], Lighter@Gray, TilePolygon[#1 + ReIm[2 Exp[I Pi/3 #2]], 2 (-#2 + 5), True, 7]} &, args]], Graph[g0, VertexSize -> 1/2, EdgeStyle -> Directive[Gray, Arrowheads[0]], VertexCoordinates -> (# -> First[#]["Coordinates"] & /@ VertexList[g0]), VertexStyle -> (# -> If[First[#]["Class"] == 0, LightGray, Hue[First[#]["Class"]/9]] & /@ VertexList[g0])] ] ]
In[25]:=
Partition[ Append[HatLeafUnderlay[ ResourceFunction["HatTrialityTree"][1, #, "Seeds" -> True] ] & /@ {0, 1, 2}, SpanFromLeft], 2] // Grid
Out[25]=

Depict a larger patch of the mutual trees triality pattern:

In[26]:=
Module[{treeData, filter}, treeData = TreeFold[Function[Flatten[Append[#2, #1]]], ResourceFunction["HatTrialityTree"][3, 3, "Seeds" -> True]]; filter = First[ReverseSortBy[WeaklyConnectedComponents[ NearestNeighborGraph[If[UnsameQ[#["Class"], 0], #["Coordinates"], Nothing] & /@ treeData, {All, 2}]], Length]]; Graphics[{EdgeForm[Gray], Map[If[Or[! MemberQ[filter, #["Coordinates"]], #["Class"] == 0], Nothing, {If[#["Symmetry"], Lighter[Red, .6], Lighter[Blue, .6]], Polygon[CirclePoints[#["Coordinates"], {2/Sqrt[3], Pi/6}, 6]]} ] &, treeData]}] ]
Out[26]=

Publisher

Brad Klee

Version History

  • 1.0.0 – 10 April 2023

Source Metadata

  • Citation:
    • David Smith, Joseph Samuel Myers, Craig S. Kaplan and Chaim Goodman-Strauss, An Aperiodic Monotile, arxiv preprint, March 20, 2023.

Related Resources

License Information