Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Enumerate possible foliations of a directed acyclic graph
ResourceFunction["GraphFoliations"][g] returns the foliations of a graph g. |
| "IncludePermutations" | False | whether to include permutations of parallel (antichain) vertices |
| "BundleFoliations" | True | whether to bundle vertices into one foliation whenever possible |
| Direction | Automatic | the direction to start building foliations (Automatic,Top or Bottom) |
| MaxItems | ∞ | set the upper limit of returned foliations |
Enumerate the foliations of a graph:
| In[1]:= | ![ResourceFunction["GraphFoliations"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8}, {
SparseArray[
Automatic, {8, 8}, 0, {1, {{0, 3, 4, 6, 7, 9, 10, 10, 10}, {{2}, {3}, {4}, {
6}, {4}, {6}, {5}, {6}, {7}, {8}}}, Pattern}], Null}, {GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{0., 5.}, {-1., 4.}}, 0.043048128342245986`], ArrowBox[{{0., 5.}, {0., 4.}}, 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQjQpEHGbympsuPrTC/snEqTurzgk7yK1fE3zr8C57
Z9+N0z5MEXao2jNT9Ozko/ayRsHTE4OFHTQ+TZ/gceycfb5D9e6znMIOPjUZ
Z9fXXLG3rtBkNt0h5PAkXUmqU+yWfdPN2LzpcUIO7+/aiEdIPLB3SpH4++WP
oIOsjXnrpNTH9jUSket9Jws6VPsxXP/86Zm9wTf51oWKgg4Rk0NF7W++sJ+h
1Dn55H0Bh3MtoT4hba/sKxa7+P+eJeDwSImhxvjXa/szFUE7zIIFHPpzQ5fc
MXlrP3XRpnPVHAIO11JCj/qbvbNf4XhKZWopv8NODob7Pf/e2Qs8v8zmdoXP
wSwy9OPk3vf2KaZNzly6fA5+YaF/Uh6/t1+ic/XWw3peB0i4fLA/ewYEeOD8
9DePvp6XRvB/JU40+lDC7cAI5bfo3mjSvcEFl2fx3/6s3RXBrz6mF/d/Dyec
/2qy3cvJdgg+WPkpDjh/jYG6lUgCgg+hORwAxiCqJQ==
"]], 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQDQEf9kNoAQcYP/j8jaOv5/PD+Rs9JCt2mfI7MEL5
EjkHxXIO8sHlWy0vLmRwRvD/bABp4IXz6y6p115SR/DZ5uWd5e/mgfNnCMty
GTzhhvONwQDBvwjSXssF5xfJHC+UOc4Jd4+wIAhwwuU3sEYDEQecH/Brif+v
Jexw/vt3IMAG5/c9tgAiBF/vRpPujSZWON8E7B5mB9+w0D8pj9/vj7uspSrX
wORgFhn6cXLv+/2zT9Xu+XqJ0WEXB8P9nn/v9n+Q0Pm5U5vR4VpK6FF/s3f7
I/aZ3s7qYnDoyw1dcsfk7f41paZHBe79t3+kxFBj/Ov1/ksy2+RUN/+zP98S
6hPS9mq/UtHbQ0JT/tpHTA4Vtb/5Yv/s0tsbbzb8sa/2Y7j++dOz/XbqDa8r
K3/by9iYt05Kfbyfb95sp5Obftq/v2sjHiHxYP/PvHncOjw/7J+lK0l1it3a
/3tmh9ui1m/2PjUZZ9fXXNkvLB/1WVv+q736p+kTPI6d2+/6T0jo5I3P9tV7
ZoqenXx0/wTzzYsqN32yl1u/JvjW4V37P52yWmq75qP9PF5z08WHVuzP3bFS
UvTYB3sGFPDBHgDzC+l0
"]], 0.043048128342245986`], ArrowBox[{{0., 4.}, {1., 3.}}, 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQjQoEHGCs4PM3jr6ezw/nb/SQrNhliuBL5BwUyznI
B+e3Wl5cyOCM4P/ZANLAC+fXXVKvvaSO4LPNyzvL380D588QluUyeMIN5xuD
AYJ/EaS9lgvOL5I5XihznBPOFxYEAQR/A2s0EHHA+QG/lvj/WsIO579/BwJs
cH7fYwsgQvD1bjTp3mhihfNNwO5hhvOvgN3DBOcXgt3DCOcLgd2D4G8Eu4cB
zl/wxXP+F8//9jD+vbsg8BfOlwUZV/gHzo8Be+g3nD9rJgj8hPPB0WX+A87/
fFgp9cHLb3A+O8j6DV8RfHD4f4Hzv/bE7vlX+RnOB0dX7Sc4H6x8ykc4PyLR
r0TjwAc4HwI+2AMAPjN8fg==
"]], 0.043048128342245986`], ArrowBox[{{1., 3.}, {1., 2.}}, 0.043048128342245986`], ArrowBox[{{1., 2.}, {0., 1.}}, 0.043048128342245986`], ArrowBox[{{1., 2.}, {1., 1.}}, 0.043048128342245986`], ArrowBox[{{0., 1.}, {0., 0.}}, 0.043048128342245986`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{0., 5.}, 0.043048128342245986], InsetBox["1", Offset[{2, 2}, {0.043048128342245986, 5.043048128342246}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-1., 4.}, 0.043048128342245986], InsetBox["2", Offset[{2, 2}, {-0.956951871657754, 4.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 4.}, 0.043048128342245986], InsetBox["3", Offset[{2, 2}, {0.043048128342245986, 4.043048128342246}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 3.}, 0.043048128342245986], InsetBox["4", Offset[{2, 2}, {1.043048128342246, 3.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 2.}, 0.043048128342245986], InsetBox["5", Offset[{2, 2}, {1.043048128342246, 2.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 1.}, 0.043048128342245986], InsetBox["6", Offset[{2, 2}, {0.043048128342245986, 1.043048128342246}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 1.}, 0.043048128342245986], InsetBox["7", Offset[{2, 2}, {1.043048128342246, 1.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 0.}, 0.043048128342245986], InsetBox["8", Offset[{2, 2}, {0.043048128342245986, 0.043048128342245986}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/449/4498d0f3-d0f5-4e29-b682-703d0e650173/45d2069d3aed41fc.png) |
| Out[1]= |
| In[2]:= | ![ResourceFunction["GraphFoliations"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8}, {
SparseArray[
Automatic, {8, 8}, 0, {1, {{0, 4, 4, 6, 8, 10, 10, 10, 10}, {{2}, {3}, {4}, {
5}, {4}, {5}, {7}, {8}, {6}, {7}}}, Pattern}], Null}, {GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{0., 3.}, {-1., 2.}}, 0.030239520958083826`], ArrowBox[{{0., 3.}, {1., 2.}}, 0.030239520958083826`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQjQo4HNRucey7nbXTfvod9okhs9gdLD0CUr1Fztjv
r726JFae3WHniUJPH77r9qWPM6yl+9kc9Ce9j5y6+YH9bt5DIb0vWR3apX9U
JHQ9s+//8+DDZj1Wh6SGS43t3G/tv6w/yt8fx+KQmGBv1Sr9yf6FesFGuUpm
h+C8uhUlbN/sc1IeXE2qY3LgyFrGPcntl31dqlhtdB6jQ9/RORaKVb/tl1U4
zIsSZ3RwYo/Ib+z8Yx+87ESo9lYGByX9G+s3lfy173i3bvFZdwYHHVvZX1us
/9m3LnrG3zzvv32Kobpfx71/9hxztVn5pv+zP8H9bbVO7H/7WWd01G0q/9pH
nOkUXrT9v7254atSXtc/9mLFj1pevP1v/+hU8sfGX7/soQHjMGsmCPyE88/f
OPp6vvkPOP/zYaXUBy+/2TNC+ezRG1ijN3yFy7PPyzvL3/0Fzv/aE7vnX+Vn
OP+Sei0QfYLzwcqnfITzIxL9SjQOfIDzIdQHewBZbqr0
"]], 0.030239520958083826`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQjQo4HGCskPM3jr6ezw7nb/KQrNhliuCL5xwUyznI
Bue3WV5cyOCM4P/dANLACufXXVKvvaSO4HPMyzvL380C588UluUyeMIM55sY
gwCCfwWkvZYJzi+UOQ5EjHC+kCAIIPgbWaM3sEYzwPkLvnjO/+L53x7Gv3cX
BP7C+bIg4wr/wPkxG0AG/IbzZ80EgZ9wPjh4zH/A+Z8PK6U+ePkNzmcHWb/h
K4IP9u8XOP9rT+yef5Wf4Xxw8NR+gvPByqd8hPMjEv1KNA58gPMh4IM9AIO9
YI0=
"]], 0.030239520958083826`], ArrowBox[{{1., 2.}, {2., 1.}}, 0.030239520958083826`], ArrowBox[{{1., 2.}, {0., 1.}}, 0.030239520958083826`], ArrowBox[{{2., 1.}, {1., 0.}}, 0.030239520958083826`], ArrowBox[{{2., 1.}, {2., 0.}}, 0.030239520958083826`], ArrowBox[{{0., 1.}, {0., 0.}}, 0.030239520958083826`], ArrowBox[{{0., 1.}, {1., 0.}}, 0.030239520958083826`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{0., 3.}, 0.030239520958083826], InsetBox["1", Offset[{2, 2}, {0.030239520958083826, 3.0302395209580837}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-1., 2.}, 0.030239520958083826], InsetBox["2", Offset[{2, 2}, {-0.9697604790419162, 2.0302395209580837}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 2.}, 0.030239520958083826], InsetBox["3", Offset[{2, 2}, {1.030239520958084, 2.0302395209580837}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{2., 1.}, 0.030239520958083826], InsetBox["4", Offset[{2, 2}, {2.0302395209580837, 1.030239520958084}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 1.}, 0.030239520958083826], InsetBox["5", Offset[{2, 2}, {0.030239520958083826, 1.030239520958084}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 0.}, 0.030239520958083826], InsetBox["6", Offset[{2, 2}, {0.030239520958083826, 0.030239520958083826}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 0.}, 0.030239520958083826], InsetBox["7", Offset[{2, 2}, {1.030239520958084, 0.030239520958083826}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{2., 0.}, 0.030239520958083826], InsetBox["8", Offset[{2, 2}, {2.0302395209580837, 0.030239520958083826}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/449/4498d0f3-d0f5-4e29-b682-703d0e650173/1f29a8f2d9e83ff8.png) |
| Out[2]= |
| In[3]:= | ![ResourceFunction["GraphFoliations"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8}, {{{1, 2}, {1, 3}, {2, 4}, {3, 4}, {2, 5}, {3, 6}, {4, 7}, {5, 7}, {4, 8}}, Null}, {FormatType -> TraditionalForm, GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{0., 3.}, {0., 2.}}, 0.030239520958083826`], ArrowBox[{{0., 3.}, {1., 2.}}, 0.030239520958083826`], ArrowBox[{{0., 2.}, {0., 1.}}, 0.030239520958083826`], ArrowBox[{{0., 2.}, {-1., 1.}}, 0.030239520958083826`], ArrowBox[{{1., 2.}, {0., 1.}}, 0.030239520958083826`], ArrowBox[{{1., 2.}, {1., 1.}}, 0.030239520958083826`], ArrowBox[{{0., 1.}, {-1., 0.}}, 0.030239520958083826`], ArrowBox[{{0., 1.}, {0., 0.}}, 0.030239520958083826`], ArrowBox[{{-1., 1.}, {-1., 0.}}, 0.030239520958083826`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{0., 3.}, 0.030239520958083826], InsetBox["1", Offset[{2, 2}, {0.030239520958083826, 3.0302395209580837}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 2.}, 0.030239520958083826], InsetBox["2", Offset[{2, 2}, {0.030239520958083826, 2.0302395209580837}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 2.}, 0.030239520958083826], InsetBox["3", Offset[{2, 2}, {1.030239520958084, 2.0302395209580837}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 1.}, 0.030239520958083826], InsetBox["4", Offset[{2, 2}, {0.030239520958083826, 1.030239520958084}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-1., 1.}, 0.030239520958083826], InsetBox["5", Offset[{2, 2}, {-0.9697604790419162, 1.030239520958084}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 1.}, 0.030239520958083826], InsetBox["6", Offset[{2, 2}, {1.030239520958084, 1.030239520958084}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-1., 0.}, 0.030239520958083826], InsetBox["7", Offset[{2, 2}, {-0.9697604790419162, 0.030239520958083826}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 0.}, 0.030239520958083826], InsetBox["8", Offset[{2, 2}, {0.030239520958083826, 0.030239520958083826}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/449/4498d0f3-d0f5-4e29-b682-703d0e650173/29653b628fa5fb13.png) |
| Out[3]= |
Bundling will combine vertices into one slice when possible; turning this off results in a greater number of foliations:
| In[4]:= | ![ResourceFunction["GraphFoliations"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8}, {
SparseArray[
Automatic, {8, 8}, 0, {1, {{0, 3, 4, 6, 7, 9, 10, 10, 10}, {{2}, {3}, {4}, {
6}, {4}, {6}, {5}, {6}, {7}, {8}}}, Pattern}], Null}, {GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{0., 5.}, {-1., 4.}}, 0.043048128342245986`], ArrowBox[{{0., 5.}, {0., 4.}}, 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQjQpEHGbympsuPrTC/snEqTurzgk7yK1fE3zr8C57
Z9+N0z5MEXao2jNT9Ozko/ayRsHTE4OFHTQ+TZ/gceycfb5D9e6znMIOPjUZ
Z9fXXLG3rtBkNt0h5PAkXUmqU+yWfdPN2LzpcUIO7+/aiEdIPLB3SpH4++WP
oIOsjXnrpNTH9jUSket9Jws6VPsxXP/86Zm9wTf51oWKgg4Rk0NF7W++sJ+h
1Dn55H0Bh3MtoT4hba/sKxa7+P+eJeDwSImhxvjXa/szFUE7zIIFHPpzQ5fc
MXlrP3XRpnPVHAIO11JCj/qbvbNf4XhKZWopv8NODob7Pf/e2Qs8v8zmdoXP
wSwy9OPk3vf2KaZNzly6fA5+YaF/Uh6/t1+ic/XWw3peB0i4fLA/ewYEeOD8
9DePvp6XRvB/JU40+lDC7cAI5bfo3mjSvcEFl2fx3/6s3RXBrz6mF/d/Dyec
/2qy3cvJdgg+WPkpDjh/jYG6lUgCgg+hORwAxiCqJQ==
"]], 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQDQEf9kNoAQcYP/j8jaOv5/PD+Rs9JCt2mfI7MEL5
EjkHxXIO8sHlWy0vLmRwRvD/bABp4IXz6y6p115SR/DZ5uWd5e/mgfNnCMty
GTzhhvONwQDBvwjSXssF5xfJHC+UOc4Jd4+wIAhwwuU3sEYDEQecH/Brif+v
Jexw/vt3IMAG5/c9tgAiBF/vRpPujSZWON8E7B5mB9+w0D8pj9/vj7uspSrX
wORgFhn6cXLv+/2zT9Xu+XqJ0WEXB8P9nn/v9n+Q0Pm5U5vR4VpK6FF/s3f7
I/aZ3s7qYnDoyw1dcsfk7f41paZHBe79t3+kxFBj/Ov1/ksy2+RUN/+zP98S
6hPS9mq/UtHbQ0JT/tpHTA4Vtb/5Yv/s0tsbbzb8sa/2Y7j++dOz/XbqDa8r
K3/by9iYt05Kfbyfb95sp5Obftq/v2sjHiHxYP/PvHncOjw/7J+lK0l1it3a
/3tmh9ui1m/2PjUZZ9fXXNkvLB/1WVv+q736p+kTPI6d2+/6T0jo5I3P9tV7
ZoqenXx0/wTzzYsqN32yl1u/JvjW4V37P52yWmq75qP9PF5z08WHVuzP3bFS
UvTYB3sGFPDBHgDzC+l0
"]], 0.043048128342245986`], ArrowBox[{{0., 4.}, {1., 3.}}, 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQjQoEHGCs4PM3jr6ezw/nb/SQrNhliuBL5BwUyznI
B+e3Wl5cyOCM4P/ZANLAC+fXXVKvvaSO4LPNyzvL380D588QluUyeMIN5xuD
AYJ/EaS9lgvOL5I5XihznBPOFxYEAQR/A2s0EHHA+QG/lvj/WsIO579/BwJs
cH7fYwsgQvD1bjTp3mhihfNNwO5hhvOvgN3DBOcXgt3DCOcLgd2D4G8Eu4cB
zl/wxXP+F8//9jD+vbsg8BfOlwUZV/gHzo8Be+g3nD9rJgj8hPPB0WX+A87/
fFgp9cHLb3A+O8j6DV8RfHD4f4Hzv/bE7vlX+RnOB0dX7Sc4H6x8ykc4PyLR
r0TjwAc4HwI+2AMAPjN8fg==
"]], 0.043048128342245986`], ArrowBox[{{1., 3.}, {1., 2.}}, 0.043048128342245986`], ArrowBox[{{1., 2.}, {0., 1.}}, 0.043048128342245986`], ArrowBox[{{1., 2.}, {1., 1.}}, 0.043048128342245986`], ArrowBox[{{0., 1.}, {0., 0.}}, 0.043048128342245986`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{0., 5.}, 0.043048128342245986], InsetBox["1", Offset[{2, 2}, {0.043048128342245986, 5.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-1., 4.}, 0.043048128342245986], InsetBox["2", Offset[{2, 2}, {-0.956951871657754, 4.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 4.}, 0.043048128342245986], InsetBox["3", Offset[{2, 2}, {0.043048128342245986, 4.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 3.}, 0.043048128342245986], InsetBox["4", Offset[{2, 2}, {1.043048128342246, 3.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 2.}, 0.043048128342245986], InsetBox["5", Offset[{2, 2}, {1.043048128342246, 2.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 1.}, 0.043048128342245986], InsetBox["6", Offset[{2, 2}, {0.043048128342245986, 1.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 1.}, 0.043048128342245986], InsetBox["7", Offset[{2, 2}, {1.043048128342246, 1.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 0.}, 0.043048128342245986], InsetBox["8", Offset[{2, 2}, {0.043048128342245986, 0.043048128342245986}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), "BundleFoliations" -> False] // Short](https://www.wolframcloud.com/obj/resourcesystem/images/449/4498d0f3-d0f5-4e29-b682-703d0e650173/2bccc771a9f2481c.png) |
| Out[4]= |
Return foliations with all possible slice permutations:
| In[5]:= | ![ResourceFunction["GraphFoliations"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8}, {
SparseArray[
Automatic, {8, 8}, 0, {1, {{0, 4, 4, 6, 8, 10, 10, 10, 10}, {{2}, {3}, {4}, {
5}, {4}, {5}, {7}, {8}, {6}, {7}}}, Pattern}], Null}, {GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{0., 3.}, {-1., 2.}}, 0.030239520958083826`], ArrowBox[{{0., 3.}, {1., 2.}}, 0.030239520958083826`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQjQo4HNRucey7nbXTfvod9okhs9gdLD0CUr1Fztjv
r726JFae3WHniUJPH77r9qWPM6yl+9kc9Ce9j5y6+YH9bt5DIb0vWR3apX9U
JHQ9s+//8+DDZj1Wh6SGS43t3G/tv6w/yt8fx+KQmGBv1Sr9yf6FesFGuUpm
h+C8uhUlbN/sc1IeXE2qY3LgyFrGPcntl31dqlhtdB6jQ9/RORaKVb/tl1U4
zIsSZ3RwYo/Ib+z8Yx+87ESo9lYGByX9G+s3lfy173i3bvFZdwYHHVvZX1us
/9m3LnrG3zzvv32Kobpfx71/9hxztVn5pv+zP8H9bbVO7H/7WWd01G0q/9pH
nOkUXrT9v7254atSXtc/9mLFj1pevP1v/+hU8sfGX7/soQHjMGsmCPyE88/f
OPp6vvkPOP/zYaXUBy+/2TNC+ezRG1ijN3yFy7PPyzvL3/0Fzv/aE7vnX+Vn
OP+Sei0QfYLzwcqnfITzIxL9SjQOfIDzIdQHewBZbqr0
"]], 0.030239520958083826`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQjQo4HGCskPM3jr6ezw7nb/KQrNhliuCL5xwUyznI
Bue3WV5cyOCM4P/dANLACufXXVKvvaSO4HPMyzvL380C588UluUyeMIM55sY
gwCCfwWkvZYJzi+UOQ5EjHC+kCAIIPgbWaM3sEYzwPkLvnjO/+L53x7Gv3cX
BP7C+bIg4wr/wPkxG0AG/IbzZ80EgZ9wPjh4zH/A+Z8PK6U+ePkNzmcHWb/h
K4IP9u8XOP9rT+yef5Wf4Xxw8NR+gvPByqd8hPMjEv1KNA58gPMh4IM9AIO9
YI0=
"]], 0.030239520958083826`], ArrowBox[{{1., 2.}, {2., 1.}}, 0.030239520958083826`], ArrowBox[{{1., 2.}, {0., 1.}}, 0.030239520958083826`], ArrowBox[{{2., 1.}, {1., 0.}}, 0.030239520958083826`], ArrowBox[{{2., 1.}, {2., 0.}}, 0.030239520958083826`], ArrowBox[{{0., 1.}, {0., 0.}}, 0.030239520958083826`], ArrowBox[{{0., 1.}, {1., 0.}}, 0.030239520958083826`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{0., 3.}, 0.030239520958083826], InsetBox["1", Offset[{2, 2}, {0.030239520958083826, 3.0302395209580837}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-1., 2.}, 0.030239520958083826], InsetBox["2", Offset[{2, 2}, {-0.9697604790419162, 2.0302395209580837}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 2.}, 0.030239520958083826], InsetBox["3", Offset[{2, 2}, {1.030239520958084, 2.0302395209580837}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{2., 1.}, 0.030239520958083826], InsetBox["4", Offset[{2, 2}, {2.0302395209580837, 1.030239520958084}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 1.}, 0.030239520958083826], InsetBox["5", Offset[{2, 2}, {0.030239520958083826, 1.030239520958084}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 0.}, 0.030239520958083826], InsetBox["6", Offset[{2, 2}, {0.030239520958083826, 0.030239520958083826}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 0.}, 0.030239520958083826], InsetBox["7", Offset[{2, 2}, {1.030239520958084, 0.030239520958083826}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{2., 0.}, 0.030239520958083826], InsetBox["8", Offset[{2, 2}, {2.0302395209580837, 0.030239520958083826}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), "IncludePermutations" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/449/4498d0f3-d0f5-4e29-b682-703d0e650173/1a1e7783254b1fb4.png) |
| Out[5]= |
| In[6]:= | ![ResourceFunction["GraphFoliations"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8}, {
SparseArray[
Automatic, {8, 8}, 0, {1, {{0, 3, 4, 6, 7, 9, 10, 10, 10}, {{2}, {3}, {4}, {
6}, {4}, {6}, {5}, {6}, {7}, {8}}}, Pattern}], Null}, {GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{0., 5.}, {-1., 4.}}, 0.043048128342245986`], ArrowBox[{{0., 5.}, {0., 4.}}, 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQjQpEHGbympsuPrTC/snEqTurzgk7yK1fE3zr8C57
Z9+N0z5MEXao2jNT9Ozko/ayRsHTE4OFHTQ+TZ/gceycfb5D9e6znMIOPjUZ
Z9fXXLG3rtBkNt0h5PAkXUmqU+yWfdPN2LzpcUIO7+/aiEdIPLB3SpH4++WP
oIOsjXnrpNTH9jUSket9Jws6VPsxXP/86Zm9wTf51oWKgg4Rk0NF7W++sJ+h
1Dn55H0Bh3MtoT4hba/sKxa7+P+eJeDwSImhxvjXa/szFUE7zIIFHPpzQ5fc
MXlrP3XRpnPVHAIO11JCj/qbvbNf4XhKZWopv8NODob7Pf/e2Qs8v8zmdoXP
wSwy9OPk3vf2KaZNzly6fA5+YaF/Uh6/t1+ic/XWw3peB0i4fLA/ewYEeOD8
9DePvp6XRvB/JU40+lDC7cAI5bfo3mjSvcEFl2fx3/6s3RXBrz6mF/d/Dyec
/2qy3cvJdgg+WPkpDjh/jYG6lUgCgg+hORwAxiCqJQ==
"]], 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQDQEf9kNoAQcYP/j8jaOv5/PD+Rs9JCt2mfI7MEL5
EjkHxXIO8sHlWy0vLmRwRvD/bABp4IXz6y6p115SR/DZ5uWd5e/mgfNnCMty
GTzhhvONwQDBvwjSXssF5xfJHC+UOc4Jd4+wIAhwwuU3sEYDEQecH/Brif+v
Jexw/vt3IMAG5/c9tgAiBF/vRpPujSZWON8E7B5mB9+w0D8pj9/vj7uspSrX
wORgFhn6cXLv+/2zT9Xu+XqJ0WEXB8P9nn/v9n+Q0Pm5U5vR4VpK6FF/s3f7
I/aZ3s7qYnDoyw1dcsfk7f41paZHBe79t3+kxFBj/Ov1/ksy2+RUN/+zP98S
6hPS9mq/UtHbQ0JT/tpHTA4Vtb/5Yv/s0tsbbzb8sa/2Y7j++dOz/XbqDa8r
K3/by9iYt05Kfbyfb95sp5Obftq/v2sjHiHxYP/PvHncOjw/7J+lK0l1it3a
/3tmh9ui1m/2PjUZZ9fXXNkvLB/1WVv+q736p+kTPI6d2+/6T0jo5I3P9tV7
ZoqenXx0/wTzzYsqN32yl1u/JvjW4V37P52yWmq75qP9PF5z08WHVuzP3bFS
UvTYB3sGFPDBHgDzC+l0
"]], 0.043048128342245986`], ArrowBox[{{0., 4.}, {1., 3.}}, 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQjQoEHGCs4PM3jr6ezw/nb/SQrNhliuBL5BwUyznI
B+e3Wl5cyOCM4P/ZANLAC+fXXVKvvaSO4LPNyzvL380D588QluUyeMIN5xuD
AYJ/EaS9lgvOL5I5XihznBPOFxYEAQR/A2s0EHHA+QG/lvj/WsIO579/BwJs
cH7fYwsgQvD1bjTp3mhihfNNwO5hhvOvgN3DBOcXgt3DCOcLgd2D4G8Eu4cB
zl/wxXP+F8//9jD+vbsg8BfOlwUZV/gHzo8Be+g3nD9rJgj8hPPB0WX+A87/
fFgp9cHLb3A+O8j6DV8RfHD4f4Hzv/bE7vlX+RnOB0dX7Sc4H6x8ykc4PyLR
r0TjwAc4HwI+2AMAPjN8fg==
"]], 0.043048128342245986`], ArrowBox[{{1., 3.}, {1., 2.}}, 0.043048128342245986`], ArrowBox[{{1., 2.}, {0., 1.}}, 0.043048128342245986`], ArrowBox[{{1., 2.}, {1., 1.}}, 0.043048128342245986`], ArrowBox[{{0., 1.}, {0., 0.}}, 0.043048128342245986`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{0., 5.}, 0.043048128342245986], InsetBox["1", Offset[{2, 2}, {0.043048128342245986, 5.043048128342246}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-1., 4.}, 0.043048128342245986], InsetBox["2", Offset[{2, 2}, {-0.956951871657754, 4.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 4.}, 0.043048128342245986], InsetBox["3", Offset[{2, 2}, {0.043048128342245986, 4.043048128342246}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 3.}, 0.043048128342245986], InsetBox["4", Offset[{2, 2}, {1.043048128342246, 3.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 2.}, 0.043048128342245986], InsetBox["5", Offset[{2, 2}, {1.043048128342246, 2.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 1.}, 0.043048128342245986], InsetBox["6", Offset[{2, 2}, {0.043048128342245986, 1.043048128342246}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 1.}, 0.043048128342245986], InsetBox["7", Offset[{2, 2}, {1.043048128342246, 1.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 0.}, 0.043048128342245986], InsetBox["8", Offset[{2, 2}, {0.043048128342245986, 0.043048128342245986}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), "IncludePermutations" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/449/4498d0f3-d0f5-4e29-b682-703d0e650173/0c1fc9f9fd9ec8e3.png) |
| Out[6]= |
Building foliations from bottom to top may result in different foliations:
| In[7]:= | ![bottom = ResourceFunction["GraphFoliations"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8}, {
SparseArray[
Automatic, {8, 8}, 0, {1, {{0, 3, 4, 6, 7, 9, 10, 10, 10}, {{2}, {3}, {4}, {
6}, {4}, {6}, {5}, {6}, {7}, {8}}}, Pattern}], Null}, {GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{0., 5.}, {-1., 4.}}, 0.043048128342245986`], ArrowBox[{{0., 5.}, {0., 4.}}, 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQjQpEHGbympsuPrTC/snEqTurzgk7yK1fE3zr8C57
Z9+N0z5MEXao2jNT9Ozko/ayRsHTE4OFHTQ+TZ/gceycfb5D9e6znMIOPjUZ
Z9fXXLG3rtBkNt0h5PAkXUmqU+yWfdPN2LzpcUIO7+/aiEdIPLB3SpH4++WP
oIOsjXnrpNTH9jUSket9Jws6VPsxXP/86Zm9wTf51oWKgg4Rk0NF7W++sJ+h
1Dn55H0Bh3MtoT4hba/sKxa7+P+eJeDwSImhxvjXa/szFUE7zIIFHPpzQ5fc
MXlrP3XRpnPVHAIO11JCj/qbvbNf4XhKZWopv8NODob7Pf/e2Qs8v8zmdoXP
wSwy9OPk3vf2KaZNzly6fA5+YaF/Uh6/t1+ic/XWw3peB0i4fLA/ewYEeOD8
9DePvp6XRvB/JU40+lDC7cAI5bfo3mjSvcEFl2fx3/6s3RXBrz6mF/d/Dyec
/2qy3cvJdgg+WPkpDjh/jYG6lUgCgg+hORwAxiCqJQ==
"]], 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQDQEf9kNoAQcYP/j8jaOv5/PD+Rs9JCt2mfI7MEL5
EjkHxXIO8sHlWy0vLmRwRvD/bABp4IXz6y6p115SR/DZ5uWd5e/mgfNnCMty
GTzhhvONwQDBvwjSXssF5xfJHC+UOc4Jd4+wIAhwwuU3sEYDEQecH/Brif+v
Jexw/vt3IMAG5/c9tgAiBF/vRpPujSZWON8E7B5mB9+w0D8pj9/vj7uspSrX
wORgFhn6cXLv+/2zT9Xu+XqJ0WEXB8P9nn/v9n+Q0Pm5U5vR4VpK6FF/s3f7
I/aZ3s7qYnDoyw1dcsfk7f41paZHBe79t3+kxFBj/Ov1/ksy2+RUN/+zP98S
6hPS9mq/UtHbQ0JT/tpHTA4Vtb/5Yv/s0tsbbzb8sa/2Y7j++dOz/XbqDa8r
K3/by9iYt05Kfbyfb95sp5Obftq/v2sjHiHxYP/PvHncOjw/7J+lK0l1it3a
/3tmh9ui1m/2PjUZZ9fXXNkvLB/1WVv+q736p+kTPI6d2+/6T0jo5I3P9tV7
ZoqenXx0/wTzzYsqN32yl1u/JvjW4V37P52yWmq75qP9PF5z08WHVuzP3bFS
UvTYB3sGFPDBHgDzC+l0
"]], 0.043048128342245986`], ArrowBox[{{0., 4.}, {1., 3.}}, 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQjQoEHGCs4PM3jr6ezw/nb/SQrNhliuBL5BwUyznI
B+e3Wl5cyOCM4P/ZANLAC+fXXVKvvaSO4LPNyzvL380D588QluUyeMIN5xuD
AYJ/EaS9lgvOL5I5XihznBPOFxYEAQR/A2s0EHHA+QG/lvj/WsIO579/BwJs
cH7fYwsgQvD1bjTp3mhihfNNwO5hhvOvgN3DBOcXgt3DCOcLgd2D4G8Eu4cB
zl/wxXP+F8//9jD+vbsg8BfOlwUZV/gHzo8Be+g3nD9rJgj8hPPB0WX+A87/
fFgp9cHLb3A+O8j6DV8RfHD4f4Hzv/bE7vlX+RnOB0dX7Sc4H6x8ykc4PyLR
r0TjwAc4HwI+2AMAPjN8fg==
"]], 0.043048128342245986`], ArrowBox[{{1., 3.}, {1., 2.}}, 0.043048128342245986`], ArrowBox[{{1., 2.}, {0., 1.}}, 0.043048128342245986`], ArrowBox[{{1., 2.}, {1., 1.}}, 0.043048128342245986`], ArrowBox[{{0., 1.}, {0., 0.}}, 0.043048128342245986`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{0., 5.}, 0.043048128342245986], InsetBox["1", Offset[{2, 2}, {0.043048128342245986, 5.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-1., 4.}, 0.043048128342245986], InsetBox["2", Offset[{2, 2}, {-0.956951871657754, 4.043048128342246}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 4.}, 0.043048128342245986], InsetBox["3", Offset[{2, 2}, {0.043048128342245986, 4.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 3.}, 0.043048128342245986], InsetBox["4", Offset[{2, 2}, {1.043048128342246, 3.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 2.}, 0.043048128342245986], InsetBox["5", Offset[{2, 2}, {1.043048128342246, 2.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 1.}, 0.043048128342245986], InsetBox["6", Offset[{2, 2}, {0.043048128342245986, 1.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 1.}, 0.043048128342245986], InsetBox["7", Offset[{2, 2}, {1.043048128342246, 1.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 0.}, 0.043048128342245986], InsetBox["8", Offset[{2, 2}, {0.043048128342245986, 0.043048128342245986}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), Direction -> Bottom];](https://www.wolframcloud.com/obj/resourcesystem/images/449/4498d0f3-d0f5-4e29-b682-703d0e650173/32dbe870429b65be.png) |
| In[8]:= | ![top = ResourceFunction["GraphFoliations"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8}, {
SparseArray[
Automatic, {8, 8}, 0, {1, {{0, 3, 4, 6, 7, 9, 10, 10, 10}, {{2}, {3}, {4}, {
6}, {4}, {6}, {5}, {6}, {7}, {8}}}, Pattern}], Null}, {GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{0., 5.}, {-1., 4.}}, 0.043048128342245986`], ArrowBox[{{0., 5.}, {0., 4.}}, 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQjQpEHGbympsuPrTC/snEqTurzgk7yK1fE3zr8C57
Z9+N0z5MEXao2jNT9Ozko/ayRsHTE4OFHTQ+TZ/gceycfb5D9e6znMIOPjUZ
Z9fXXLG3rtBkNt0h5PAkXUmqU+yWfdPN2LzpcUIO7+/aiEdIPLB3SpH4++WP
oIOsjXnrpNTH9jUSket9Jws6VPsxXP/86Zm9wTf51oWKgg4Rk0NF7W++sJ+h
1Dn55H0Bh3MtoT4hba/sKxa7+P+eJeDwSImhxvjXa/szFUE7zIIFHPpzQ5fc
MXlrP3XRpnPVHAIO11JCj/qbvbNf4XhKZWopv8NODob7Pf/e2Qs8v8zmdoXP
wSwy9OPk3vf2KaZNzly6fA5+YaF/Uh6/t1+ic/XWw3peB0i4fLA/ewYEeOD8
9DePvp6XRvB/JU40+lDC7cAI5bfo3mjSvcEFl2fx3/6s3RXBrz6mF/d/Dyec
/2qy3cvJdgg+WPkpDjh/jYG6lUgCgg+hORwAxiCqJQ==
"]], 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQDQEf9kNoAQcYP/j8jaOv5/PD+Rs9JCt2mfI7MEL5
EjkHxXIO8sHlWy0vLmRwRvD/bABp4IXz6y6p115SR/DZ5uWd5e/mgfNnCMty
GTzhhvONwQDBvwjSXssF5xfJHC+UOc4Jd4+wIAhwwuU3sEYDEQecH/Brif+v
Jexw/vt3IMAG5/c9tgAiBF/vRpPujSZWON8E7B5mB9+w0D8pj9/vj7uspSrX
wORgFhn6cXLv+/2zT9Xu+XqJ0WEXB8P9nn/v9n+Q0Pm5U5vR4VpK6FF/s3f7
I/aZ3s7qYnDoyw1dcsfk7f41paZHBe79t3+kxFBj/Ov1/ksy2+RUN/+zP98S
6hPS9mq/UtHbQ0JT/tpHTA4Vtb/5Yv/s0tsbbzb8sa/2Y7j++dOz/XbqDa8r
K3/by9iYt05Kfbyfb95sp5Obftq/v2sjHiHxYP/PvHncOjw/7J+lK0l1it3a
/3tmh9ui1m/2PjUZZ9fXXNkvLB/1WVv+q736p+kTPI6d2+/6T0jo5I3P9tV7
ZoqenXx0/wTzzYsqN32yl1u/JvjW4V37P52yWmq75qP9PF5z08WHVuzP3bFS
UvTYB3sGFPDBHgDzC+l0
"]], 0.043048128342245986`], ArrowBox[{{0., 4.}, {1., 3.}}, 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQjQoEHGCs4PM3jr6ezw/nb/SQrNhliuBL5BwUyznI
B+e3Wl5cyOCM4P/ZANLAC+fXXVKvvaSO4LPNyzvL380D588QluUyeMIN5xuD
AYJ/EaS9lgvOL5I5XihznBPOFxYEAQR/A2s0EHHA+QG/lvj/WsIO579/BwJs
cH7fYwsgQvD1bjTp3mhihfNNwO5hhvOvgN3DBOcXgt3DCOcLgd2D4G8Eu4cB
zl/wxXP+F8//9jD+vbsg8BfOlwUZV/gHzo8Be+g3nD9rJgj8hPPB0WX+A87/
fFgp9cHLb3A+O8j6DV8RfHD4f4Hzv/bE7vlX+RnOB0dX7Sc4H6x8ykc4PyLR
r0TjwAc4HwI+2AMAPjN8fg==
"]], 0.043048128342245986`], ArrowBox[{{1., 3.}, {1., 2.}}, 0.043048128342245986`], ArrowBox[{{1., 2.}, {0., 1.}}, 0.043048128342245986`], ArrowBox[{{1., 2.}, {1., 1.}}, 0.043048128342245986`], ArrowBox[{{0., 1.}, {0., 0.}}, 0.043048128342245986`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{0., 5.}, 0.043048128342245986], InsetBox["1", Offset[{2, 2}, {0.043048128342245986, 5.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-1., 4.}, 0.043048128342245986], InsetBox["2", Offset[{2, 2}, {-0.956951871657754, 4.043048128342246}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 4.}, 0.043048128342245986], InsetBox["3", Offset[{2, 2}, {0.043048128342245986, 4.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 3.}, 0.043048128342245986], InsetBox["4", Offset[{2, 2}, {1.043048128342246, 3.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 2.}, 0.043048128342245986], InsetBox["5", Offset[{2, 2}, {1.043048128342246, 2.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 1.}, 0.043048128342245986], InsetBox["6", Offset[{2, 2}, {0.043048128342245986, 1.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 1.}, 0.043048128342245986], InsetBox["7", Offset[{2, 2}, {1.043048128342246, 1.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 0.}, 0.043048128342245986], InsetBox["8", Offset[{2, 2}, {0.043048128342245986, 0.043048128342245986}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), Direction -> Top];](https://www.wolframcloud.com/obj/resourcesystem/images/449/4498d0f3-d0f5-4e29-b682-703d0e650173/3ca169d4462571f2.png) |
| In[9]:= |
| Out[9]= |
Direction will not matter when all permutations are included:
| In[10]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/933e4292-5253-4b9a-aa25-891b5b629257"]](https://www.wolframcloud.com/obj/resourcesystem/images/449/4498d0f3-d0f5-4e29-b682-703d0e650173/6fd7b17da45bc26a.png) |
| In[11]:= |
| Out[11]= |
Limit the enumeration with an upper bound:
| In[12]:= | ![ResourceFunction["GraphFoliations"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8}, {
SparseArray[
Automatic, {8, 8}, 0, {1, {{0, 3, 4, 6, 7, 9, 10, 10, 10}, {{2}, {3}, {4}, {
6}, {4}, {6}, {5}, {6}, {7}, {8}}}, Pattern}], Null}, {GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{0., 5.}, {-1., 4.}}, 0.043048128342245986`], ArrowBox[{{0., 5.}, {0., 4.}}, 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQjQpEHGbympsuPrTC/snEqTurzgk7yK1fE3zr8C57
Z9+N0z5MEXao2jNT9Ozko/ayRsHTE4OFHTQ+TZ/gceycfb5D9e6znMIOPjUZ
Z9fXXLG3rtBkNt0h5PAkXUmqU+yWfdPN2LzpcUIO7+/aiEdIPLB3SpH4++WP
oIOsjXnrpNTH9jUSket9Jws6VPsxXP/86Zm9wTf51oWKgg4Rk0NF7W++sJ+h
1Dn55H0Bh3MtoT4hba/sKxa7+P+eJeDwSImhxvjXa/szFUE7zIIFHPpzQ5fc
MXlrP3XRpnPVHAIO11JCj/qbvbNf4XhKZWopv8NODob7Pf/e2Qs8v8zmdoXP
wSwy9OPk3vf2KaZNzly6fA5+YaF/Uh6/t1+ic/XWw3peB0i4fLA/ewYEeOD8
9DePvp6XRvB/JU40+lDC7cAI5bfo3mjSvcEFl2fx3/6s3RXBrz6mF/d/Dyec
/2qy3cvJdgg+WPkpDjh/jYG6lUgCgg+hORwAxiCqJQ==
"]], 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQDQEf9kNoAQcYP/j8jaOv5/PD+Rs9JCt2mfI7MEL5
EjkHxXIO8sHlWy0vLmRwRvD/bABp4IXz6y6p115SR/DZ5uWd5e/mgfNnCMty
GTzhhvONwQDBvwjSXssF5xfJHC+UOc4Jd4+wIAhwwuU3sEYDEQecH/Brif+v
Jexw/vt3IMAG5/c9tgAiBF/vRpPujSZWON8E7B5mB9+w0D8pj9/vj7uspSrX
wORgFhn6cXLv+/2zT9Xu+XqJ0WEXB8P9nn/v9n+Q0Pm5U5vR4VpK6FF/s3f7
I/aZ3s7qYnDoyw1dcsfk7f41paZHBe79t3+kxFBj/Ov1/ksy2+RUN/+zP98S
6hPS9mq/UtHbQ0JT/tpHTA4Vtb/5Yv/s0tsbbzb8sa/2Y7j++dOz/XbqDa8r
K3/by9iYt05Kfbyfb95sp5Obftq/v2sjHiHxYP/PvHncOjw/7J+lK0l1it3a
/3tmh9ui1m/2PjUZZ9fXXNkvLB/1WVv+q736p+kTPI6d2+/6T0jo5I3P9tV7
ZoqenXx0/wTzzYsqN32yl1u/JvjW4V37P52yWmq75qP9PF5z08WHVuzP3bFS
UvTYB3sGFPDBHgDzC+l0
"]], 0.043048128342245986`], ArrowBox[{{0., 4.}, {1., 3.}}, 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQjQoEHGCs4PM3jr6ezw/nb/SQrNhliuBL5BwUyznI
B+e3Wl5cyOCM4P/ZANLAC+fXXVKvvaSO4LPNyzvL380D588QluUyeMIN5xuD
AYJ/EaS9lgvOL5I5XihznBPOFxYEAQR/A2s0EHHA+QG/lvj/WsIO579/BwJs
cH7fYwsgQvD1bjTp3mhihfNNwO5hhvOvgN3DBOcXgt3DCOcLgd2D4G8Eu4cB
zl/wxXP+F8//9jD+vbsg8BfOlwUZV/gHzo8Be+g3nD9rJgj8hPPB0WX+A87/
fFgp9cHLb3A+O8j6DV8RfHD4f4Hzv/bE7vlX+RnOB0dX7Sc4H6x8ykc4PyLR
r0TjwAc4HwI+2AMAPjN8fg==
"]], 0.043048128342245986`], ArrowBox[{{1., 3.}, {1., 2.}}, 0.043048128342245986`], ArrowBox[{{1., 2.}, {0., 1.}}, 0.043048128342245986`], ArrowBox[{{1., 2.}, {1., 1.}}, 0.043048128342245986`], ArrowBox[{{0., 1.}, {0., 0.}}, 0.043048128342245986`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{0., 5.}, 0.043048128342245986], InsetBox["1", Offset[{2, 2}, {0.043048128342245986, 5.043048128342246}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-1., 4.}, 0.043048128342245986], InsetBox["2", Offset[{2, 2}, {-0.956951871657754, 4.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 4.}, 0.043048128342245986], InsetBox["3", Offset[{2, 2}, {0.043048128342245986, 4.043048128342246}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 3.}, 0.043048128342245986], InsetBox["4", Offset[{2, 2}, {1.043048128342246, 3.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 2.}, 0.043048128342245986], InsetBox["5", Offset[{2, 2}, {1.043048128342246, 2.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 1.}, 0.043048128342245986], InsetBox["6", Offset[{2, 2}, {0.043048128342245986, 1.043048128342246}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 1.}, 0.043048128342245986], InsetBox["7", Offset[{2, 2}, {1.043048128342246, 1.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 0.}, 0.043048128342245986], InsetBox["8", Offset[{2, 2}, {0.043048128342245986, 0.043048128342245986}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\), "BundleFoliations" -> False, "IncludePermutations" -> True, MaxItems -> 3]](https://www.wolframcloud.com/obj/resourcesystem/images/449/4498d0f3-d0f5-4e29-b682-703d0e650173/311cbaebe56e0142.png) |
| Out[12]= |
Use foliations for a graph generated with the resource function LayeredLayoutGraph:
| In[13]:= | ![With[{graph = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8}, {
SparseArray[
Automatic, {8, 8}, 0, {1, {{0, 3, 4, 6, 7, 9, 10, 10, 10}, {{2}, {3}, {4}, {
6}, {4}, {6}, {5}, {6}, {7}, {8}}}, Pattern}], Null}, {GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{0., 5.}, {-1., 4.}}, 0.043048128342245986`], ArrowBox[{{0., 5.}, {0., 4.}}, 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQjQpEHGbympsuPrTC/snEqTurzgk7yK1fE3zr8C57
Z9+N0z5MEXao2jNT9Ozko/ayRsHTE4OFHTQ+TZ/gceycfb5D9e6znMIOPjUZ
Z9fXXLG3rtBkNt0h5PAkXUmqU+yWfdPN2LzpcUIO7+/aiEdIPLB3SpH4++WP
oIOsjXnrpNTH9jUSket9Jws6VPsxXP/86Zm9wTf51oWKgg4Rk0NF7W++sJ+h
1Dn55H0Bh3MtoT4hba/sKxa7+P+eJeDwSImhxvjXa/szFUE7zIIFHPpzQ5fc
MXlrP3XRpnPVHAIO11JCj/qbvbNf4XhKZWopv8NODob7Pf/e2Qs8v8zmdoXP
wSwy9OPk3vf2KaZNzly6fA5+YaF/Uh6/t1+ic/XWw3peB0i4fLA/ewYEeOD8
9DePvp6XRvB/JU40+lDC7cAI5bfo3mjSvcEFl2fx3/6s3RXBrz6mF/d/Dyec
/2qy3cvJdgg+WPkpDjh/jYG6lUgCgg+hORwAxiCqJQ==
"]], 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQDQEf9kNoAQcYP/j8jaOv5/PD+Rs9JCt2mfI7MEL5
EjkHxXIO8sHlWy0vLmRwRvD/bABp4IXz6y6p115SR/DZ5uWd5e/mgfNnCMty
GTzhhvONwQDBvwjSXssF5xfJHC+UOc4Jd4+wIAhwwuU3sEYDEQecH/Brif+v
Jexw/vt3IMAG5/c9tgAiBF/vRpPujSZWON8E7B5mB9+w0D8pj9/vj7uspSrX
wORgFhn6cXLv+/2zT9Xu+XqJ0WEXB8P9nn/v9n+Q0Pm5U5vR4VpK6FF/s3f7
I/aZ3s7qYnDoyw1dcsfk7f41paZHBe79t3+kxFBj/Ov1/ksy2+RUN/+zP98S
6hPS9mq/UtHbQ0JT/tpHTA4Vtb/5Yv/s0tsbbzb8sa/2Y7j++dOz/XbqDa8r
K3/by9iYt05Kfbyfb95sp5Obftq/v2sjHiHxYP/PvHncOjw/7J+lK0l1it3a
/3tmh9ui1m/2PjUZZ9fXXNkvLB/1WVv+q736p+kTPI6d2+/6T0jo5I3P9tV7
ZoqenXx0/wTzzYsqN32yl1u/JvjW4V37P52yWmq75qP9PF5z08WHVuzP3bFS
UvTYB3sGFPDBHgDzC+l0
"]], 0.043048128342245986`], ArrowBox[{{0., 4.}, {1., 3.}}, 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQjQoEHGCs4PM3jr6ezw/nb/SQrNhliuBL5BwUyznI
B+e3Wl5cyOCM4P/ZANLAC+fXXVKvvaSO4LPNyzvL380D588QluUyeMIN5xuD
AYJ/EaS9lgvOL5I5XihznBPOFxYEAQR/A2s0EHHA+QG/lvj/WsIO579/BwJs
cH7fYwsgQvD1bjTp3mhihfNNwO5hhvOvgN3DBOcXgt3DCOcLgd2D4G8Eu4cB
zl/wxXP+F8//9jD+vbsg8BfOlwUZV/gHzo8Be+g3nD9rJgj8hPPB0WX+A87/
fFgp9cHLb3A+O8j6DV8RfHD4f4Hzv/bE7vlX+RnOB0dX7Sc4H6x8ykc4PyLR
r0TjwAc4HwI+2AMAPjN8fg==
"]], 0.043048128342245986`], ArrowBox[{{1., 3.}, {1., 2.}}, 0.043048128342245986`], ArrowBox[{{1., 2.}, {0., 1.}}, 0.043048128342245986`], ArrowBox[{{1., 2.}, {1., 1.}}, 0.043048128342245986`], ArrowBox[{{0., 1.}, {0., 0.}}, 0.043048128342245986`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{0., 5.}, 0.043048128342245986], InsetBox["1", Offset[{2, 2}, {0.043048128342245986, 5.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-1., 4.}, 0.043048128342245986], InsetBox["2", Offset[{2, 2}, {-0.956951871657754, 4.043048128342246}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 4.}, 0.043048128342245986], InsetBox["3", Offset[{2, 2}, {0.043048128342245986, 4.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 3.}, 0.043048128342245986], InsetBox["4", Offset[{2, 2}, {1.043048128342246, 3.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 2.}, 0.043048128342245986], InsetBox["5", Offset[{2, 2}, {1.043048128342246, 2.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 1.}, 0.043048128342245986], InsetBox["6", Offset[{2, 2}, {0.043048128342245986, 1.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{1., 1.}, 0.043048128342245986], InsetBox["7", Offset[{2, 2}, {1.043048128342246, 1.043048128342246}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 0.}, 0.043048128342245986], InsetBox["8", Offset[{2, 2}, {0.043048128342245986, 0.043048128342245986}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\)},
ResourceFunction["LayeredLayoutGraph"][graph, #] & /@ ResourceFunction["GraphFoliations"][graph]
]](https://www.wolframcloud.com/obj/resourcesystem/images/449/4498d0f3-d0f5-4e29-b682-703d0e650173/07c7ac12730caaaf.png) |
| Out[13]= | 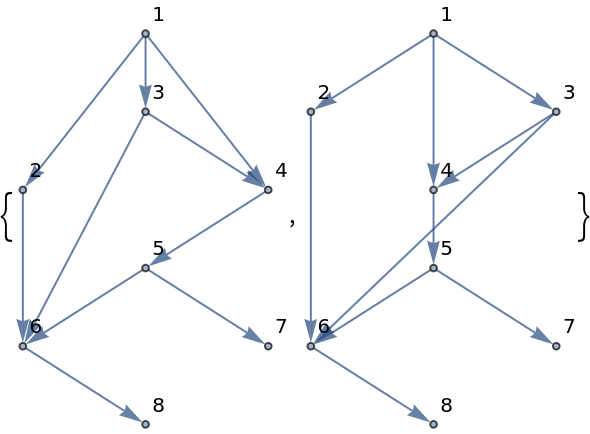 |
This work is licensed under a Creative Commons Attribution 4.0 International License