Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 GoldbergGraph

Source Notebook

Create a graph corresponding to a Goldberg polyhedron

Contributed by: Jan Mangaldan

ResourceFunction["GoldbergGraph"][base,n]

gives a graph corresponding to an order-n Goldberg polyhedron based on the polyhedron base.

ResourceFunction["GoldbergGraph"][base,class,n]

gives a graph corresponding to an order-n Goldberg polyhedron of class class, based on the polyhedron base.

Details and Options

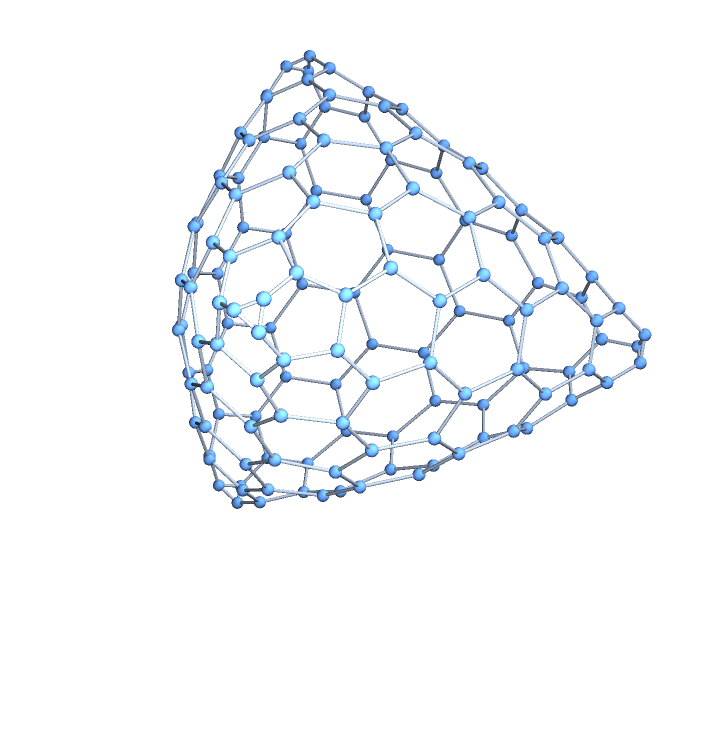
Possible values of base are "Tetrahedron", "Octahedron" or "Icosahedron".
Possible values of class include "I", "II", 1 and 2.
ResourceFunction["GoldbergGraph"][base,n] is equivalent to ResourceFunction["GoldbergGraph"][base,2,n].
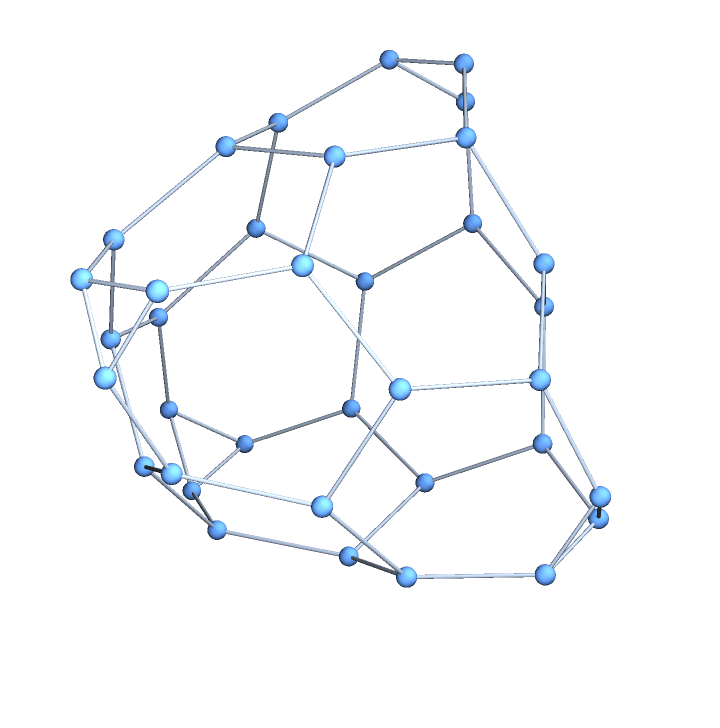
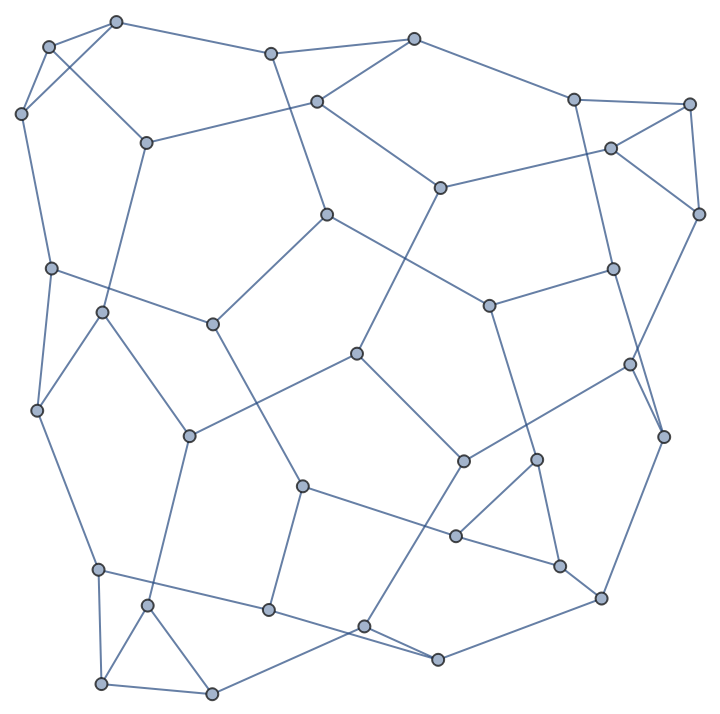
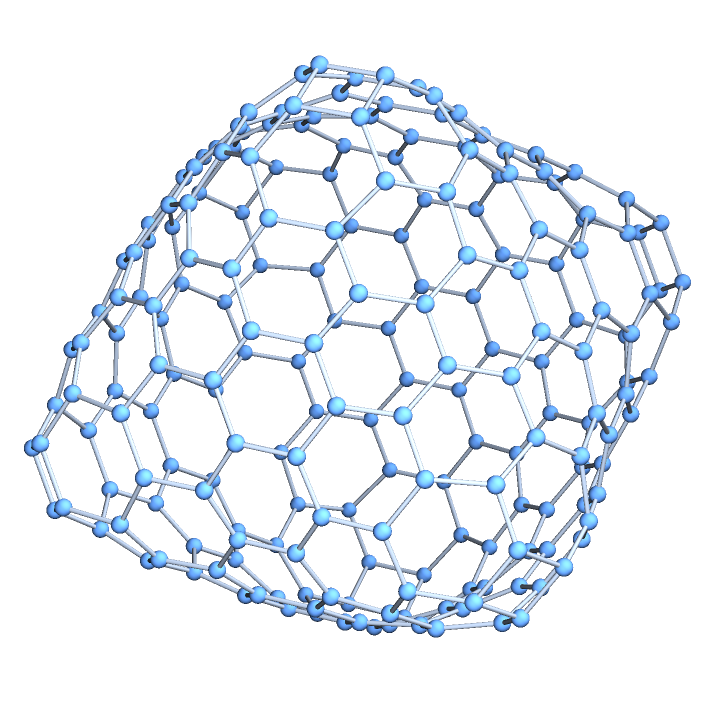
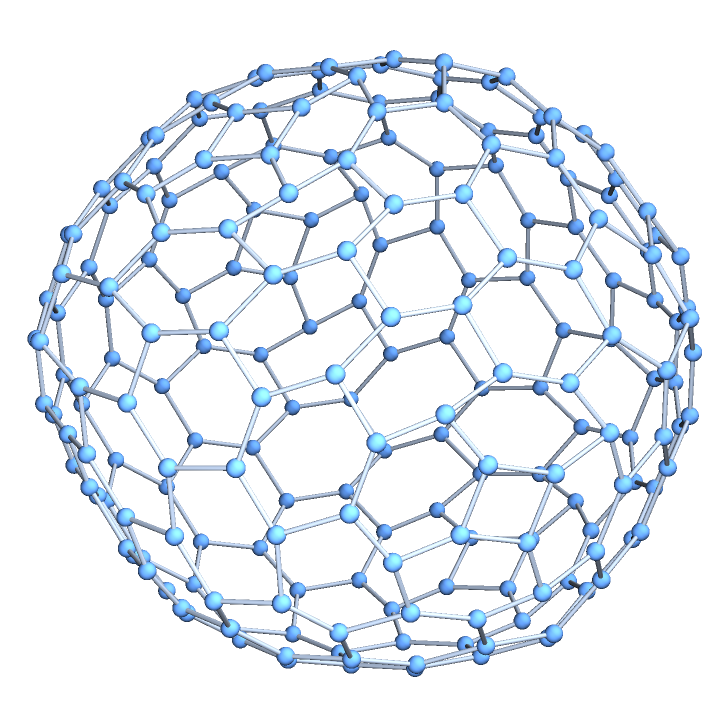
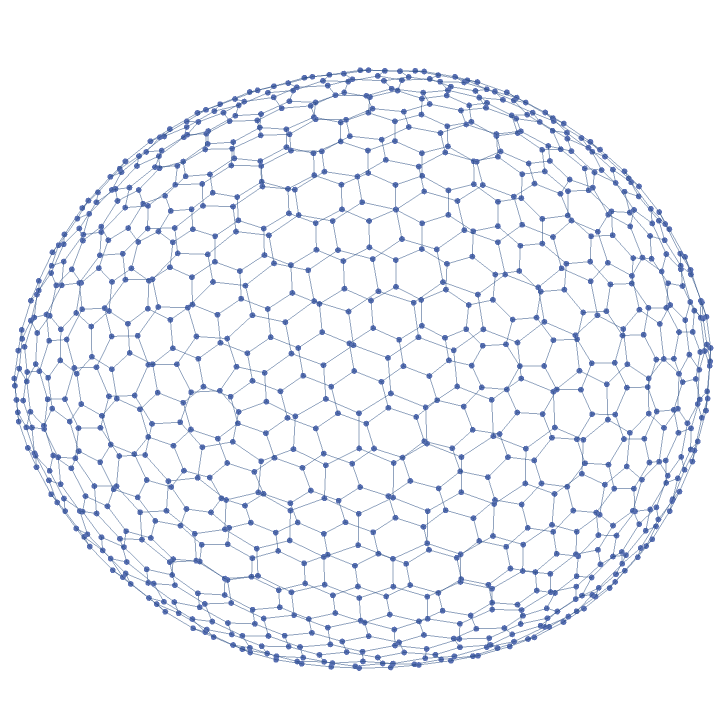
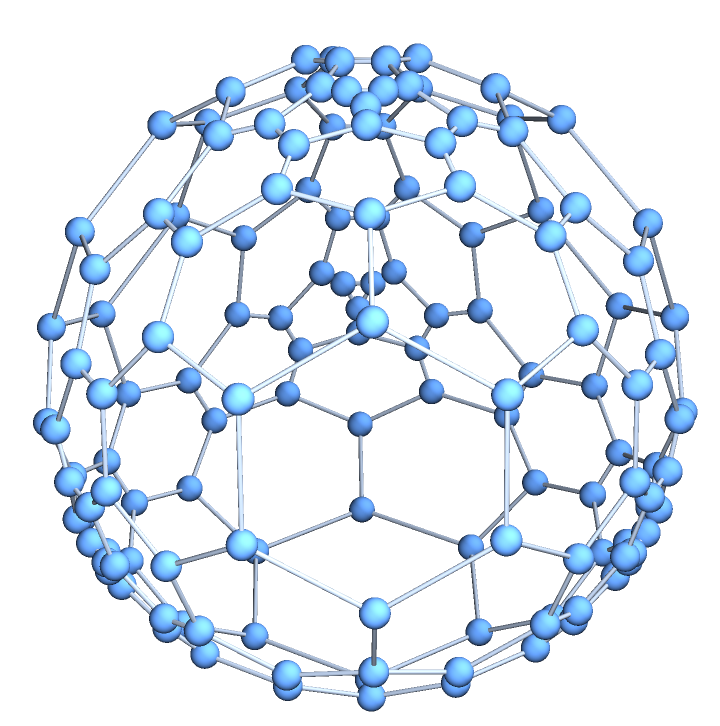
ResourceFunction["GoldbergGraph"][base,1,n] or ResourceFunction["GoldbergGraph"][base,"I",n] generates a three-dimensional graph corresponding to the class I (n+1,0) Goldberg polyhedron, the dual polyhedron of a geodesic sphere.
ResourceFunction["GoldbergGraph"][base,2,n] or ResourceFunction["GoldbergGraph"][base,"II",n] generates a three-dimensional graph corresponding to the class II (n,n) Goldberg polyhedron.
ResourceFunction["GoldbergGraph"] takes the same options as Graph3D.
With the setting VertexCoordinates→"Embedded", coordinates corresponding to the vertices of the Goldberg graph are generated with a special method.

Examples

Basic Examples (2) 

Generate a Goldberg graph corresponding to the truncated icosahedron (buckyball):

In[1]:=
ResourceFunction["GoldbergGraph"]["Icosahedron", 1]
Out[1]=

The result is isomorphic with a truncated icosahedron:

In[2]:=
IsomorphicGraphQ[%, PolyhedronData["TruncatedIcosahedron", "Skeleton"]]
Out[2]=

Generate a class I, order-3 Goldberg graph with an octahedral base and specially computed coordinates for the vertices:

In[3]:=
ResourceFunction["GoldbergGraph"]["Octahedron", "I", 3, VertexCoordinates -> "Embedded"]
Out[3]=

Scope (2) 

Goldberg graphs corresponding to the Platonic solids:

In[4]:=
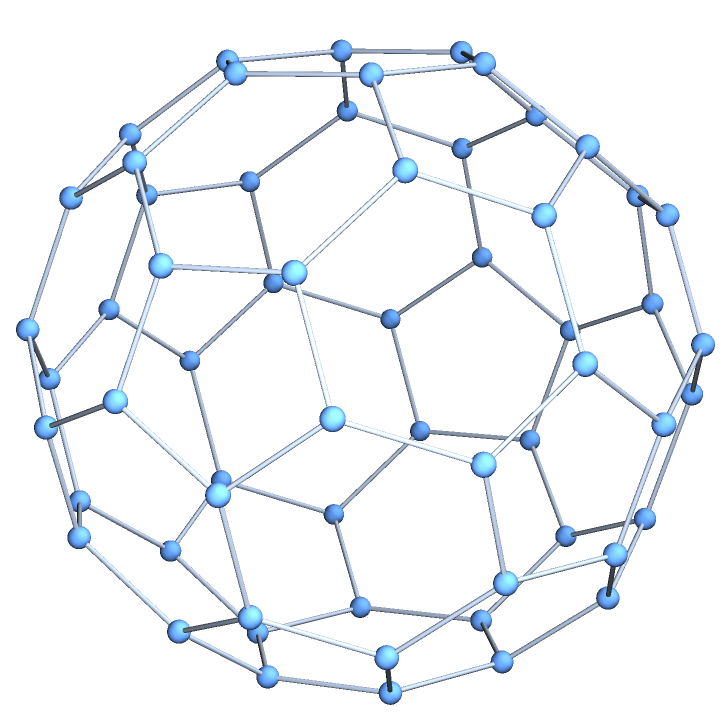
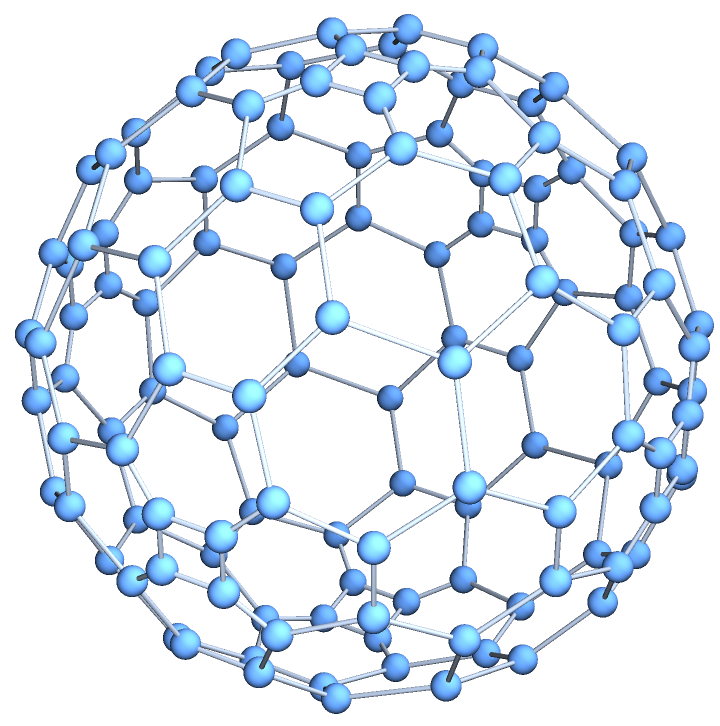
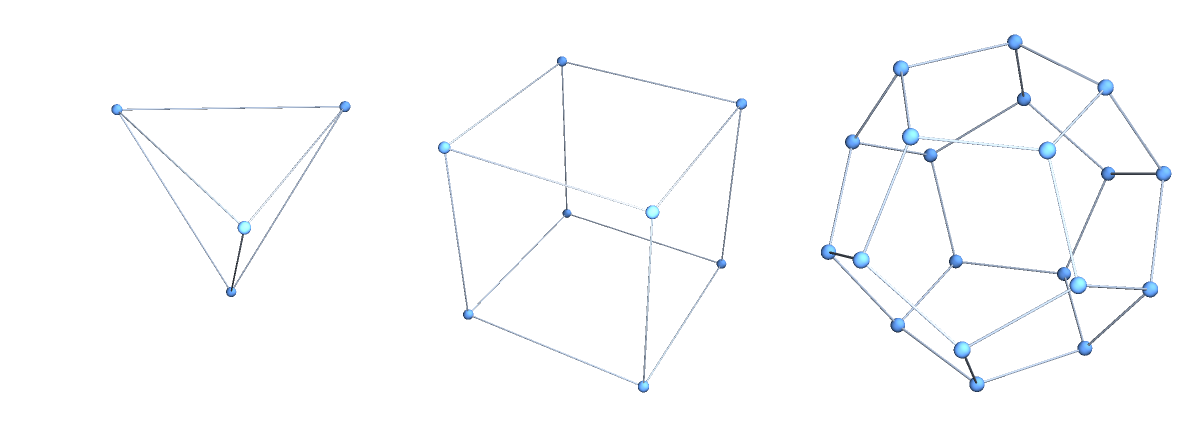
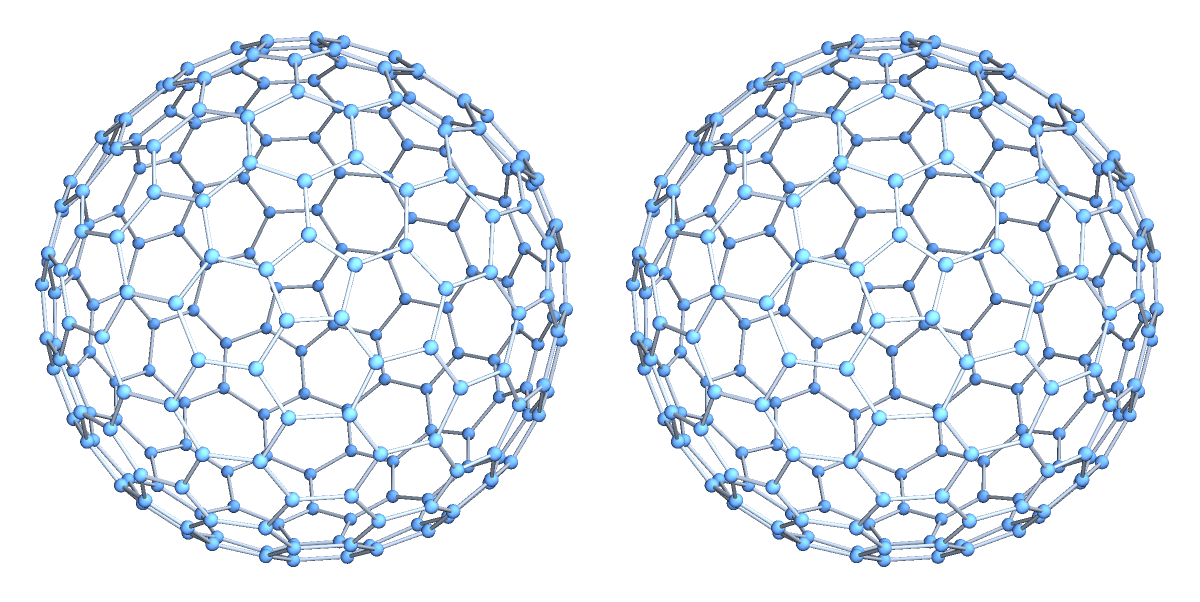
Table[ResourceFunction["GoldbergGraph"][p, 0, VertexCoordinates -> "Embedded"], {p, {"Tetrahedron", "Octahedron", "Icosahedron"}}] // GraphicsRow
Out[4]=

Generate a class I Goldberg graph with a tetrahedral base:

In[5]:=
ResourceFunction["GoldbergGraph"]["Tetrahedron", 1, 2]
Out[5]=

Convert to a standard Graph object:

In[6]:=
% // Graph
Out[6]=

Options (4) 

GraphLayout (1) 

Specify various layouts for the Goldberg graph:

In[7]:=
ResourceFunction["GoldbergGraph"]["Octahedron", 3, GraphLayout -> "SpringEmbedding"]
Out[7]=
In[8]:=
ResourceFunction["GoldbergGraph"]["Octahedron", 3, GraphLayout -> "HighDimensionalEmbedding"]
Out[8]=

PlotTheme (1) 

Use a large graph theme:

In[9]:=
ResourceFunction["GoldbergGraph"]["Icosahedron", 4, PlotTheme -> "LargeNetworkDefault"]
Out[9]=

VertexCoordinates (2) 

By default, vertex coordinates are computed automatically, depending on the setting for GraphLayout:

In[10]:=
ResourceFunction["GoldbergGraph"]["Tetrahedron", 1, 5]
Out[10]=

Use specially computed coordinates for the vertices:

In[11]:=
ResourceFunction["GoldbergGraph"]["Tetrahedron", 1, 5, VertexCoordinates -> "Embedded"]
Out[11]=

Properties and Relations (1) 

Resource function BuckyballGraph is a special case of GoldbergGraph:

In[12]:=
{ResourceFunction["GoldbergGraph"]["Icosahedron", 2], ResourceFunction["BuckyballGraph"][2]} // GraphicsRow
Out[12]=

Version History

  • 1.0.1 – 24 January 2022
  • 1.0.0 – 10 February 2021

Source Metadata

Related Resources

Author Notes

Class III Goldberg polyhedra are currently not supported, and will be implemented in a future update.

License Information