Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Show the Gershgorin disks of a square matrix
ResourceFunction["GershgorinDisks"][m] gives a Region representing the union of the Gershgorin disks of the square matrix m. | |
ResourceFunction["GershgorinDisks"][m,out] gives a result of the type specified by out. |
| "Region" | a Region representing the union of the Gershgorin disks |
| "List" | a list of Disk objects representing the Gershgorin disks |
The Gershgorin disks of a machine-precision matrix:
| In[1]:= |
| Out[1]= |  |
Show the Gershgorin disks along with the eigenvalues:
| In[2]:= |
| Out[2]= | 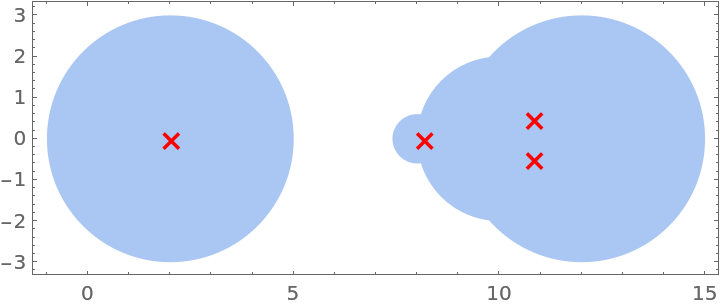 |
Gershgorin disks of an exact matrix:
| In[3]:= |
| Out[3]= |  |
List the individual disks comprising the region:
| In[4]:= |
| Out[4]= |
Gershgorin disks of a complex matrix:
| In[5]:= |
| Out[5]= |  |
List the individual disks comprising the region:
| In[6]:= |
| Out[6]= |
Gershgorin disks of a SparseArray:
| In[7]:= |
| Out[7]= |  |
Compare the Gershgorin disks of an unsymmetric matrix and its transpose:
| In[8]:= | ![BlockRandom[SeedRandom[54321]; mat = RandomVariate[NormalDistribution[], {12, 12}, WorkingPrecision -> 25]];
{Graphics[{Directive[
FaceForm[
Opacity[0.4,
Hue[0.5]]],
EdgeForm[
Directive[
Opacity[
Rational[1, 2],
GrayLevel[0]],
AbsoluteThickness[
Rational[1, 2]]]]], ReverseSortBy[ResourceFunction["GershgorinDisks"][mat, "List"], Last]}, Frame -> True], Graphics[{Directive[
FaceForm[
Opacity[0.4,
Hue[0.5]]],
EdgeForm[
Directive[
Opacity[
Rational[1, 2],
GrayLevel[0]],
AbsoluteThickness[
Rational[1, 2]]]]], ReverseSortBy[
ResourceFunction["GershgorinDisks"][Transpose[mat], "List"], Last]}, Frame -> True]}](https://www.wolframcloud.com/obj/resourcesystem/images/5fa/5fafe2f2-4777-419b-9fdd-00764415f841/61711eff6b270541.png) |
| Out[8]= | 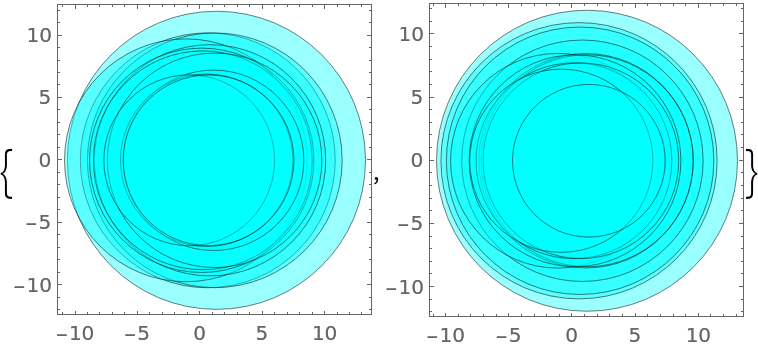 |
Show the intersection of the two sets of Gershgorin disks along with the eigenvalues:
| In[9]:= | ![Show[Region[
RegionIntersection[ResourceFunction["GershgorinDisks"][mat], ResourceFunction["GershgorinDisks"][Transpose[mat]]]], ComplexListPlot[Eigenvalues[mat], PlotMarkers -> {"\[Times]", Large},
PlotStyle -> Red], Frame -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/5fa/5fafe2f2-4777-419b-9fdd-00764415f841/29a61a1f9fb1c30f.png) |
| Out[9]= | 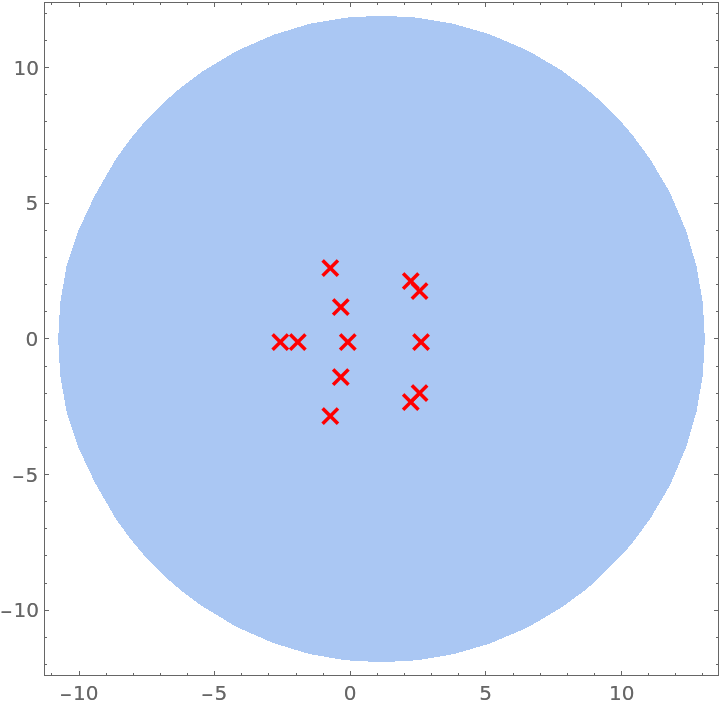 |
A random matrix:
| In[10]:= |
| Out[10]= | 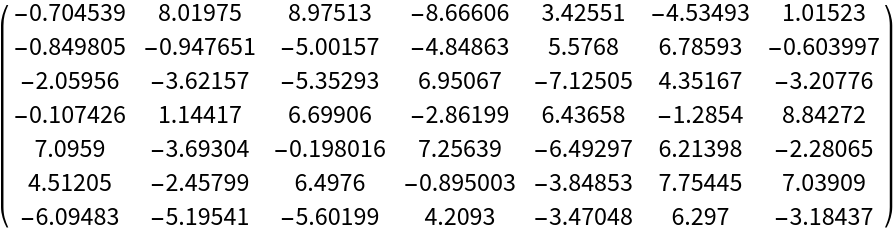 |
Use HessenbergDecomposition to transform it to a similar upper Hessenberg matrix:
| In[11]:= |
| Out[11]= | 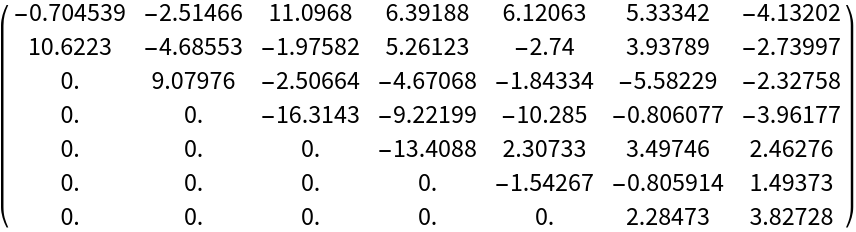 |
Compare the Gershgorin disks of the original and transformed matrices:
| In[12]:= | ![eigs = Eigenvalues[hes]; {Graphics[{{Directive[
FaceForm[
Opacity[0.4,
Hue[0.5]]],
EdgeForm[
Directive[
Opacity[
Rational[1, 2],
GrayLevel[0]],
AbsoluteThickness[
Rational[1, 2]]]]], ReverseSortBy[ResourceFunction["GershgorinDisks"][mat, "List"], Last]}, {Directive[Red, AbsolutePointSize[4]], Point[ReIm[eigs]]}}, Frame -> True], Graphics[{{Directive[
FaceForm[
Opacity[0.4,
Hue[0.5]]],
EdgeForm[
Directive[
Opacity[
Rational[1, 2],
GrayLevel[0]],
AbsoluteThickness[
Rational[1, 2]]]]], ReverseSortBy[ResourceFunction["GershgorinDisks"][hes, "List"], Last]}, {Directive[Red, AbsolutePointSize[4]], Point[ReIm[eigs]]}}, Frame -> True]}](https://www.wolframcloud.com/obj/resourcesystem/images/5fa/5fafe2f2-4777-419b-9fdd-00764415f841/6387ba25e0c19b60.png) |
| Out[12]= | 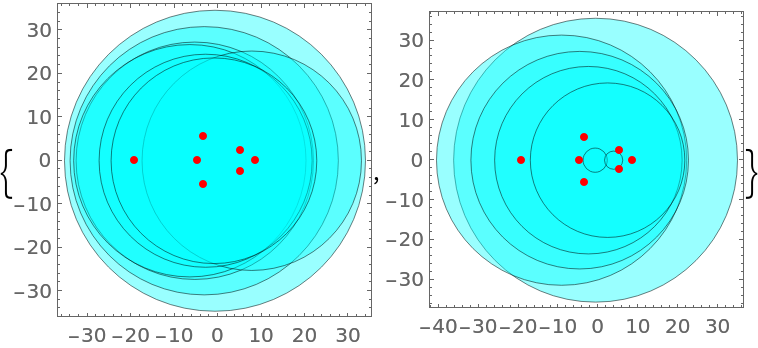 |
Compare the Gershgorin disks of two different companion matrices of a given polynomial:
| In[13]:= | ![poly = 5 + 4 x + 3 x^2 + 2 x^3 + x^4 + x^5;
rts = x /. NSolve[poly, x];
mfro = ResourceFunction["GeneralizedFiedlerMatrix"][Range[5, 1, -1], poly, x];
mfie = ResourceFunction["GeneralizedFiedlerMatrix"][poly, x];
{Graphics[{{Directive[
FaceForm[
Opacity[0.4,
Hue[0.5]]],
EdgeForm[
Directive[
Opacity[
Rational[1, 2],
GrayLevel[0]],
AbsoluteThickness[
Rational[1, 2]]]]], ReverseSortBy[ResourceFunction["GershgorinDisks"][mfro, "List"], Last]}, {Directive[Red, AbsolutePointSize[4]], Point[ReIm[rts]]}}, Frame -> True, PlotLabel -> "Frobenius"], Graphics[{{Directive[
FaceForm[
Opacity[0.4,
Hue[0.5]]],
EdgeForm[
Directive[
Opacity[
Rational[1, 2],
GrayLevel[0]],
AbsoluteThickness[
Rational[1, 2]]]]], ReverseSortBy[ResourceFunction["GershgorinDisks"][mfie, "List"], Last]}, {Directive[Red, AbsolutePointSize[4]], Point[ReIm[rts]]}}, Frame -> True, PlotLabel -> "Fiedler"]}](https://www.wolframcloud.com/obj/resourcesystem/images/5fa/5fafe2f2-4777-419b-9fdd-00764415f841/3fc9332921b2ec1d.png) |
| Out[13]= | 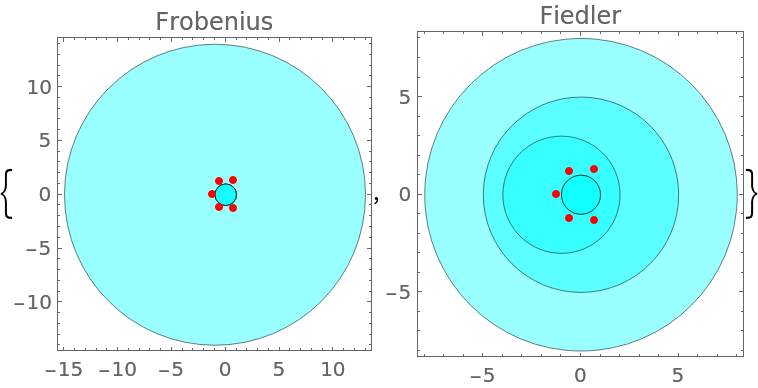 |
The Gershgorin disks of a matrix enclose all of the matrix's eigenvalues:
| In[14]:= | ![BlockRandom[SeedRandom[14344]; mat = RandomVariate[NormalDistribution[], {5, 5}]];
gd = ResourceFunction["GershgorinDisks"][mat]; eigs = Eigenvalues[mat];
RegionMember[gd][ReIm[eigs]]](https://www.wolframcloud.com/obj/resourcesystem/images/5fa/5fafe2f2-4777-419b-9fdd-00764415f841/052da5f33e709cb2.png) |
| Out[14]= |
The Gershgorin disks of a diagonal matrix is a set of disks with zero radius:
| In[15]:= |
| Out[15]= |
| In[16]:= |
| Out[16]= |
This work is licensed under a Creative Commons Attribution 4.0 International License