Details
A tiling pattern is any rectangular array of non-negative integers.
A template is a rectangular array containing non-negative integers or
Blank (_) values.
A
Blank value in a template can match any integer in a tiling pattern.
For example, the template
{{_,0,2},{0,1,_}} has four different integer values and two
Blank (_) values.
ResourceFunction["GenerateTiling"] assumes that possible values in a tiling pattern are bounded above by the maximum integer found in the set of templates.
Sets of potentially many templates should have the same bounding size, say {a,b}.
If all {a,b} subarrays of an {m,n} pattern match a template from input templates, the tiling pattern is said to be "consistent with local constraints listed in templates", or for short, "template consistent".
Values on the edge of a pattern should be checked against partial templates by allowing complete templates to partially intersect the tiling pattern and ignoring the overhang to exterior.
ResourceFunction["GenerateTiling"] takes the option "Boundary". When set to "Periodic", ResourceFunction["GenerateTiling"] also requires template consistency of a tiling pattern across North-South and East-West edges (i.e. toroidal boundary conditions).


![tiles = {{{0, 1}, {1, 0}}, {{1, 0}, {1, 1}}, {{1, 1}, {0, 1}}};
tiling = ResourceFunction["GenerateTiling"][tiles, {}, 20];
Labeled[ArrayPlot[
tiling, {Frame -> False, Mesh -> None, PixelConstrained -> 10}],
Row[ResourceFunction["TilingPatternPlot"][tiles, ImageSize -> 50], Spacer[20]], Spacings -> {1, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/9cc/9ccab8a8-7d8a-41ce-a17a-f3e2faa0d035/60318f4ae3af8958.png)

![tiles = {{{0, 1}, {1, 0}}, {{1, 0}, {1, 1}}, {{1, 1}, {0, 1}}};
tiling = ResourceFunction["GenerateTiling"][tiles, {}, {10, 20}];
Labeled[ArrayPlot[tiling,
{Frame -> False, Mesh -> None, PixelConstrained -> 10}],
Row[ArrayPlot[#, ImageSize -> 50, Mesh -> True] & /@ Union[Flatten[Partition[tiling, {2, 2}, {1, 1}], 1]],
Spacer[5]], Spacings -> {1, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/9cc/9ccab8a8-7d8a-41ce-a17a-f3e2faa0d035/060eb0a700af2dbf.png)

![With[{tiling = ResourceFunction["GenerateTiling"][
Partition[RotateRight[Range[0, 3], #], 2] & /@ Range[4], {}, {20, 20}],
colRules = MapIndexed[(#2[[1]] - 1) -> #1 &,
{Blend[{Yellow, Orange}], Blend[{Green, Cyan}, .5],
Lighter[Blue, .5], Lighter[Blend[{Magenta, Red}, .25], 0.4]}]},
Labeled[ArrayPlot[tiling, ColorRules -> colRules,
{Frame -> False, Mesh -> True, MeshStyle -> Black}],
Row[ArrayPlot[#, ColorRules -> colRules,
ImageSize -> 50, Mesh -> True, MeshStyle -> Black
] & /@ Union[Flatten[Partition[tiling, {2, 2}, {1, 1}], 1]],
Spacer[5]], Spacings -> {1, 1}]]](https://www.wolframcloud.com/obj/resourcesystem/images/9cc/9ccab8a8-7d8a-41ce-a17a-f3e2faa0d035/58df5b95fa40ff4b.png)
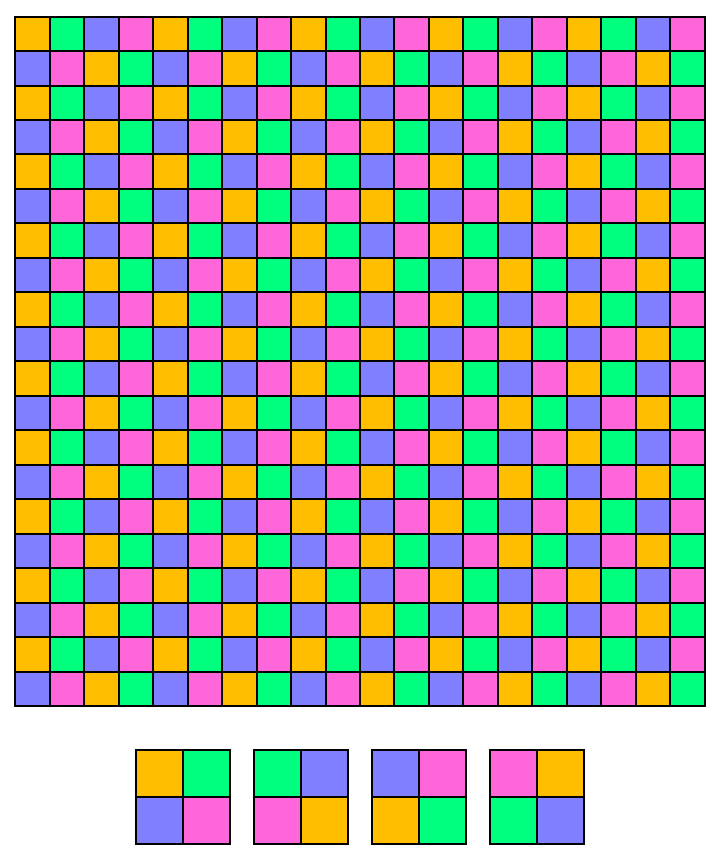
![With[{tilings = ResourceFunction["GenerateTiling"][
Partition[RotateRight[Range[0, 3], #], 2] & /@ Range[4], {}, {12, 12}, All],
colRules = MapIndexed[(#2[[1]] - 1) -> #1 &,
{Blend[{Yellow, Orange}], Blend[{Green, Cyan}, .5],
Lighter[Blue, .5], Lighter[Blend[{Magenta, Red}, .25], 0.4]}]},
ArrayPlot[#, ColorRules -> colRules,
{Frame -> False, Mesh -> True, MeshStyle -> Black}] & /@ tilings]](https://www.wolframcloud.com/obj/resourcesystem/images/9cc/9ccab8a8-7d8a-41ce-a17a-f3e2faa0d035/3adaab557fc0f7d1.png)
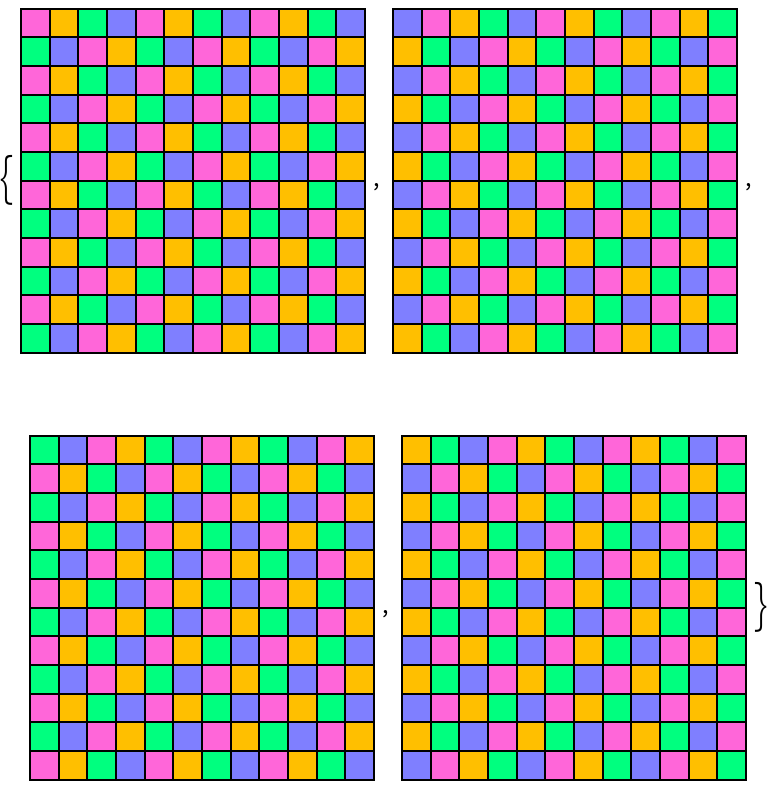
![With[{tiles = {{{0, 1, 1}, {1, 1, 1}}, {{1, 0, 1}, {1, 1, 1}}, {{1, 1,
0}, {1, 1, 1}}, {{1, 1, 1}, {1, 0, 1}}, {{0, 1, 0}, {0, 0, 0}}, {{
0, 0, 0}, {0, 0, 1}}, {{0, 0, 0}, {0, 1, 0}}, {{0, 0, 0}, {1, 0, 0}}, {{1, 0, 1}, {0, 0, 0}}, {{1, 1, 1}, {0, 1, 0}}, {{0, 0, 1}, {
0, 1, 1}}, {{0, 1, 0}, {1, 1, 0}}, {{1, 0, 0}, {1, 0, 1}}}},
Labeled[ArrayPlot[ResourceFunction["GenerateTiling"][tiles, {}, 30],
{Frame -> False, Mesh -> None, PixelConstrained -> 10}],
Grid[Partition[Append[
ArrayPlot[#, ImageSize -> 50, Mesh -> True] & /@ tiles, ""], 7],
Spacings -> {1, 1}], Spacings -> {1, 1}]]](https://www.wolframcloud.com/obj/resourcesystem/images/9cc/9ccab8a8-7d8a-41ce-a17a-f3e2faa0d035/36102ce176c1c2df.png)

![With[{tiles = Map[{{#[[1]], #[[2]]},
{#[[2]], #[[3]]}} &,
RotateRight[Range[3], #] & /@ Range[0, 2]]},
ArrayPlot[ResourceFunction["GenerateTiling"][tiles, {{#}}, 5],
Frame -> None, ColorRules -> {
1 -> Lighter[Blend[{Red, Orange}], .25],
2 -> Darker[Blend[{Green, Yellow}, .6], .1],
3 -> Lighter[Blend[{Blue, Green}, .2], .35]}
] & /@ Range[3]]](https://www.wolframcloud.com/obj/resourcesystem/images/9cc/9ccab8a8-7d8a-41ce-a17a-f3e2faa0d035/0fdf4fdd26bace69.png)

![With[{tiles = Map[{{#[[1]], #[[2]]},
{#[[2]], #[[3]]}} &,
RotateRight[Range[3], #] & /@ Range[0, 2]]},
ResourceFunction["GenerateTiling"][tiles, {{#, #}}, 5] & /@ Range[3]]](https://www.wolframcloud.com/obj/resourcesystem/images/9cc/9ccab8a8-7d8a-41ce-a17a-f3e2faa0d035/506147628faa8bc9.png)
![With[{tiles = {{{0, 1, 1}, {1, 1, 1}}, {{1, 0, 1}, {1, 1, 1}}, {{1, 1,
0}, {1, 1, 1}}, {{1, 1, 1}, {1, 0, 1}}, {{0, 1, 0}, {0, 0, 0}}, {{
0, 0, 0}, {0, 0, 1}}, {{0, 0, 0}, {0, 1, 0}}, {{0, 0, 0}, {1, 0, 0}}, {{1, 0, 1}, {0, 0, 0}}, {{1, 1, 1}, {0, 1, 0}}, {{0, 0, 1}, {
0, 1, 1}}, {{0, 1, 0}, {1, 1, 0}}, {{1, 0, 0}, {1, 0, 1}}}},
ArrayPlot[
ResourceFunction["GenerateTiling"][tiles, {}, 30, "Boundary" -> "Periodic"],
{Frame -> False, Mesh -> None}]]](https://www.wolframcloud.com/obj/resourcesystem/images/9cc/9ccab8a8-7d8a-41ce-a17a-f3e2faa0d035/513710668b382d0c.png)

![With[{tiles = {{{0, 1, 1}, {1, 1, 1}}, {{1, 0, 1}, {1, 1, 1}}, {{1, 1,
0}, {1, 1, 1}}, {{1, 1, 1}, {1, 0, 1}}, {{0, 1, 0}, {0, 0, 0}}, {{
0, 0, 0}, {0, 0, 1}}, {{0, 0, 0}, {0, 1, 0}}, {{0, 0, 0}, {1, 0, 0}}, {{1, 0, 1}, {0, 0, 0}}, {{1, 1, 1}, {0, 1, 0}}, {{0, 0, 1}, {
0, 1, 1}}, {{0, 1, 0}, {1, 1, 0}}, {{1, 0, 0}, {1, 0, 1}}}},
ArrayPlot[ResourceFunction["GenerateTiling"][tiles, {}, {5, 6},
"Boundary" -> "Periodic"],
Frame -> False, Mesh -> None, PixelConstrained -> 10]]](https://www.wolframcloud.com/obj/resourcesystem/images/9cc/9ccab8a8-7d8a-41ce-a17a-f3e2faa0d035/2c8e1eff7963fa06.png)

![With[{tiles = {{{0, 1, 1}, {1, 1, 1}}, {{1, 0, 1}, {1, 1, 1}}, {{1, 1,
0}, {1, 1, 1}}, {{1, 1, 1}, {1, 0, 1}}, {{0, 1, 0}, {0, 0, 0}}, {{
0, 0, 0}, {0, 0, 1}}, {{0, 0, 0}, {0, 1, 0}}, {{0, 0, 0}, {1, 0, 0}}, {{1, 0, 1}, {0, 0, 0}}, {{1, 1, 1}, {0, 1, 0}}, {{0, 0, 1}, {
0, 1, 1}}, {{0, 1, 0}, {1, 1, 0}}, {{1, 0, 0}, {1, 0, 1}}}},
Length@ResourceFunction["GenerateTiling"][tiles, {}, {5, 6}, All,
"Boundary" -> "Periodic"]]](https://www.wolframcloud.com/obj/resourcesystem/images/9cc/9ccab8a8-7d8a-41ce-a17a-f3e2faa0d035/4c8bddb822e8afd7.png)
![With[{tiles = {{{0, 0,
Blank[]}, {0,
Blank[], 0}, {1,
Blank[],
Blank[]}}, {{0, 0,
Blank[]}, {0,
Blank[], 1}, {0,
Blank[],
Blank[]}}, {{0, 0,
Blank[]}, {1,
Blank[], 0}, {0,
Blank[],
Blank[]}}, {{0, 0,
Blank[]}, {1,
Blank[], 0}, {1,
Blank[],
Blank[]}}, {{0, 1,
Blank[]}, {0,
Blank[], 0}, {1,
Blank[],
Blank[]}}, {{0, 1,
Blank[]}, {0,
Blank[], 1}, {0,
Blank[],
Blank[]}}, {{0, 1,
Blank[]}, {1,
Blank[], 1}, {1,
Blank[],
Blank[]}}, {{1, 0,
Blank[]}, {0,
Blank[], 0}, {1,
Blank[],
Blank[]}}, {{1, 0,
Blank[]}, {1,
Blank[], 0}, {0,
Blank[],
Blank[]}}, {{1, 0,
Blank[]}, {1,
Blank[], 1}, {1,
Blank[],
Blank[]}}, {{1, 1,
Blank[]}, {0,
Blank[], 0}, {0,
Blank[],
Blank[]}}, {{1, 1,
Blank[]}, {0,
Blank[], 0}, {1,
Blank[],
Blank[]}}, {{1, 1,
Blank[]}, {1,
Blank[], 0}, {0,
Blank[],
Blank[]}}, {{1, 1,
Blank[]}, {1,
Blank[], 1}, {0,
Blank[],
Blank[]}}}},
Labeled[
ArrayPlot[
ResourceFunction["GenerateTiling"][tiles, {}, 79, "Boundary" -> "Periodic"],
{Frame -> False, Mesh -> None, PixelConstrained -> 4}],
Labeled[Grid[Partition[Append[ArrayPlot[#, ImageSize -> 50,
Mesh -> True, ColorRules -> {Verbatim[_] -> Gray}
] & /@ tiles, ""], 7], Spacings -> {1, 1}],
Text@Style[
"(Gray squares in templates stand for Blank wildcards)",
Gray]], Spacings -> {1, 1}]]](https://www.wolframcloud.com/obj/resourcesystem/images/9cc/9ccab8a8-7d8a-41ce-a17a-f3e2faa0d035/0169e5e07099ecc7.png)

![With[{tiles = {{{
Blank[], 1,
Blank[]}, {1, 0, 0}, {
Blank[], 0,
Blank[]}}, {{
Blank[], 1,
Blank[]}, {0, 1, 0}, {
Blank[], 0,
Blank[]}}, {{
Blank[], 1,
Blank[]}, {0, 0, 1}, {
Blank[], 1,
Blank[]}}, {{
Blank[], 1,
Blank[]}, {0, 0, 1}, {
Blank[], 0,
Blank[]}}, {{
Blank[], 1,
Blank[]}, {0, 0, 0}, {
Blank[], 1,
Blank[]}}, {{
Blank[], 0,
Blank[]}, {1, 1, 1}, {
Blank[], 0,
Blank[]}}, {{
Blank[], 0,
Blank[]}, {1, 0, 1}, {
Blank[], 1,
Blank[]}}, {{
Blank[], 0,
Blank[]}, {1, 0, 0}, {
Blank[], 1,
Blank[]}}, {{
Blank[], 0,
Blank[]}, {0, 1, 1}, {
Blank[], 1,
Blank[]}}, {{
Blank[], 0,
Blank[]}, {0, 1, 0}, {
Blank[], 0,
Blank[]}}, {{
Blank[], 0,
Blank[]}, {0, 0, 1}, {
Blank[], 0,
Blank[]}}, {{
Blank[], 0,
Blank[]}, {0, 0, 0}, {
Blank[], 0,
Blank[]}}}},
Labeled[
ArrayPlot[ResourceFunction["GenerateTiling"][tiles, {{1}, {1}}, 100],
{Frame -> False, Mesh -> None, PixelConstrained -> 4}],
Labeled[Grid[Partition[ArrayPlot[#, ImageSize -> 50,
Mesh -> True, ColorRules -> {0 -> White, 1 -> Black, _ -> Gray}
] & /@ tiles, 6], Spacings -> {1, 1}],
Text@Style[
"(Gray squares in templates stand for Blank wildcards)",
Gray]], Spacings -> {1, 1}]]](https://www.wolframcloud.com/obj/resourcesystem/images/9cc/9ccab8a8-7d8a-41ce-a17a-f3e2faa0d035/6df9584e2bb31448.png)
