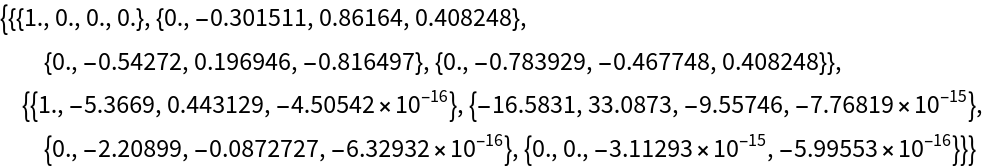Basic Examples (2)
Find the Gaussian Hessenberg decomposition of a 4×4 matrix:
The matrix h is an upper Hessenberg matrix:
Scope (6)
The Gaussian Hessenberg decomposition for a complex matrix:
The Gaussian Hessenberg decomposition for a numeric matrix:
The Gaussian Hessenberg decomposition for a matrix with entries having 24digit precision:
The Gaussian Hessenberg decomposition for a symbolic matrix:
The Gaussian Hessenberg-triangular decomposition for an exact matrix pencil:
The Gaussian Hessenberg-triangular decomposition for a numeric matrix pencil:
Properties and Relations (3)
A 4×4 matrix:
Compute its Gaussian Hessenberg decomposition:
The matrix h is upper Hessenberg:
The original matrix m is given by p.h.Inverse[p]:
A pair of 4×4 matrices:
Compute the Gaussian Hessenberg-triangular decomposition of the corresponding pencil:
The matrix h is upper Hessenberg:
The matrix t is upper triangular:
The matrix m is given by q.h.p:
The matrix a is given by q.t.p:
GaussianHessenbergDecomposition gives a different result from the built-in HessenbergDecomposition:
Both decompositions yield upper Hessenberg matrices that are similar to the original matrix:
HessenbergDecomposition yields a unitary transformation matrix, while GaussianHessenbergDecomposition does not:
![{p, h} = ResourceFunction["GaussianHessenbergDecomposition"][\!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "2", "3", "5"},
{"2", "4", "1", "6"},
{"1", "2",
RowBox[{"-", "1"}], "3"},
{"2", "0", "1", "3"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/449/44958af3-db05-4fae-8af8-f41768a8bed3/57db1ba61444548c.png)

![ResourceFunction["GaussianHessenbergDecomposition"][({
{1 + I, 3 + I, 2 - I, 1 + I},
{3 + I, 2 - I, 1 + I, 3 + I},
{4 + I, 5 + I, 6 - I, 2 + I},
{1 + I, 3 - I, 3 - I, 2 - I}
})]](https://www.wolframcloud.com/obj/resourcesystem/images/449/44958af3-db05-4fae-8af8-f41768a8bed3/36f3ca38c56ca596.png)
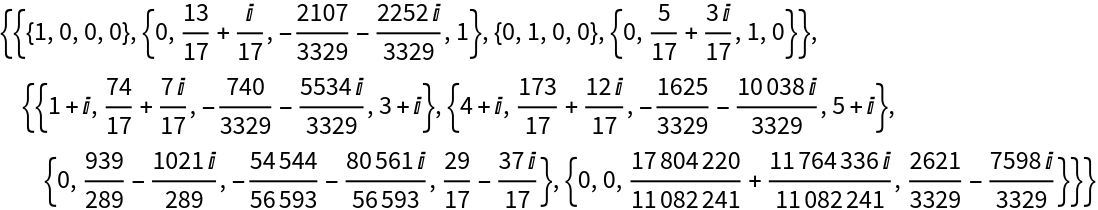

![ResourceFunction["GaussianHessenbergDecomposition"][({
{1., 2., 3., 4.},
{5., 6., 7., 8.},
{9., 10., 11., 12.},
{13., 14., 15., 16.}
})]](https://www.wolframcloud.com/obj/resourcesystem/images/449/44958af3-db05-4fae-8af8-f41768a8bed3/2bf48cb33e354a1d.png)

![ResourceFunction["GaussianHessenbergDecomposition"][N[({
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
{13, 14, 15, 16}
}), 24]]](https://www.wolframcloud.com/obj/resourcesystem/images/449/44958af3-db05-4fae-8af8-f41768a8bed3/4c6590921011ff79.png)

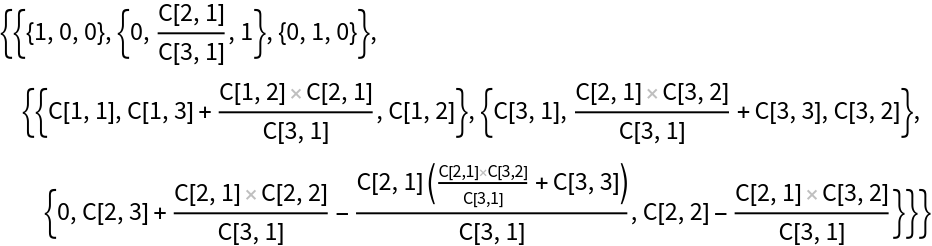
![MatrixForm /@ ResourceFunction["GaussianHessenbergDecomposition"][{( {
{50, -60, 50, -27, 6, 6},
{38, -28, 27, -17, 5, 5},
{27, -17, 27, -17, 5, 5},
{27, -28, 38, -17, 5, 5},
{27, -28, 27, -17, 16, 5},
{27, -28, 27, -17, 5, 16}
} ), ( {
{16, 5, 5, 5, -6, 5},
{5, 16, 5, 5, -6, 5},
{5, 5, 16, 5, -6, 5},
{5, 5, 5, 16, -6, 5},
{5, 5, 5, 5, -6, 16},
{6, 6, 6, 6, -5, 6}
} )}]](https://www.wolframcloud.com/obj/resourcesystem/images/449/44958af3-db05-4fae-8af8-f41768a8bed3/273f04a7a755a311.png)

![MatrixForm /@ ResourceFunction["GaussianHessenbergDecomposition"][{N[( {
{50, -60, 50, -27, 6, 6},
{38, -28, 27, -17, 5, 5},
{27, -17, 27, -17, 5, 5},
{27, -28, 38, -17, 5, 5},
{27, -28, 27, -17, 16, 5},
{27, -28, 27, -17, 5, 16}
} )], N[( {
{16, 5, 5, 5, -6, 5},
{5, 16, 5, 5, -6, 5},
{5, 5, 16, 5, -6, 5},
{5, 5, 5, 16, -6, 5},
{5, 5, 5, 5, -6, 16},
{6, 6, 6, 6, -5, 6}
} )]}]](https://www.wolframcloud.com/obj/resourcesystem/images/449/44958af3-db05-4fae-8af8-f41768a8bed3/060bc1fcc75c3e81.png)

![m = \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "2", "3", "5"},
{"2", "4", "1", "6"},
{"1", "2",
RowBox[{"-", "1"}], "3"},
{"2", "0", "1", "3"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\);](https://www.wolframcloud.com/obj/resourcesystem/images/449/44958af3-db05-4fae-8af8-f41768a8bed3/32f3e7d5f39f0d18.png)
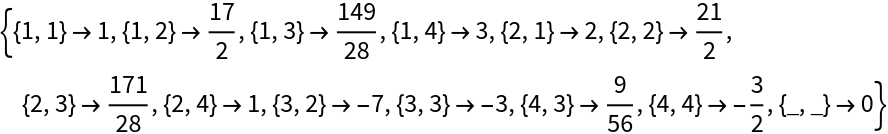
![m = \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "2", "3", "5"},
{"2", "4", "1", "6"},
{"1", "2",
RowBox[{"-", "1"}], "3"},
{"2", "0", "1", "3"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\); a = ( {
{-17, 27, -17, 5},
{-28, 38, -17, 5},
{-28, 27, -17, 16},
{-28, 27, -17, 5}
} );](https://www.wolframcloud.com/obj/resourcesystem/images/449/44958af3-db05-4fae-8af8-f41768a8bed3/5c059cd71caf436d.png)
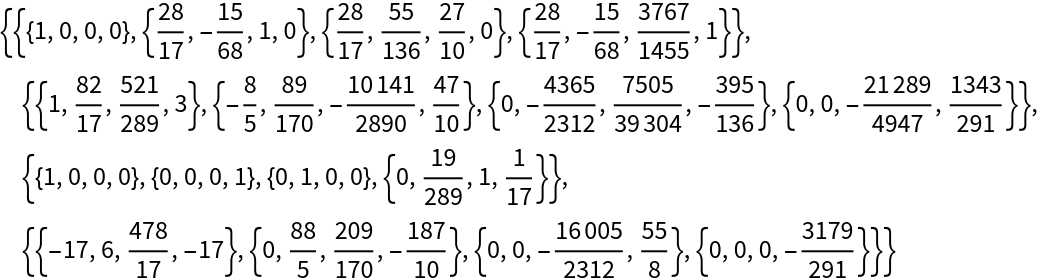
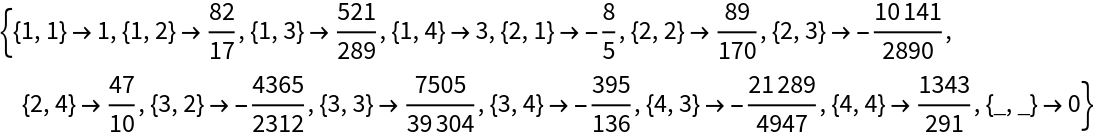
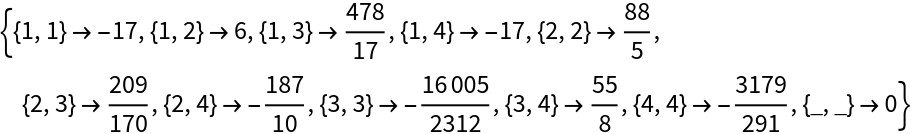
![m = N[({
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
{13, 14, 15, 16}
})];](https://www.wolframcloud.com/obj/resourcesystem/images/449/44958af3-db05-4fae-8af8-f41768a8bed3/1fe6494f7c4411e1.png)