Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 GainRescale

Source Notebook

Apply a flatter or steeper variation in the middle of an interval

Contributed by: Jan Mangaldan

ResourceFunction["GainRescale"][a,x]

biases x to be flatter towards the middle if a<1/2, and steeper towards the middle if a>1/2, as x runs from 0 to 1.

ResourceFunction["GainRescale"][a,x,{min,max}]

biases x as x runs from min to max.

ResourceFunction["GainRescale"][a,x,{min,max},{ymin,ymax}]

biases x as x runs from min to max, with the result rescaled to run from ymin to ymax.

Details and Options

a can be any real number between 0 and 1.
ResourceFunction["GainRescale"] is a symmetrized version of the resource function BiasedRescale.
The result of ResourceFunction["GainRescale"][a,x,{min,max}] is always between 0 and 1.
ResourceFunction["GainRescale"] can take the Method option for the bias function to use. Possible settings for the Method option are "Schlick" (default) and "Perlin".
With the default option setting Method→"Schlick", ResourceFunction["GainRescale"] uses Schlick's bias function x/((1/a-2)(1-x)+1).
With Method→"Perlin", ResourceFunction["GainRescale"] uses Perlin's bias function x-log2(a).
ResourceFunction["GainRescale"] is commonly used in computer graphics.

Examples

Basic Examples (3) 

Evaluate numerically:

In[1]:=
ResourceFunction["GainRescale"][1/8, 0.6]
Out[1]=

Plot over a subset of the reals:

In[2]:=
Plot[ResourceFunction["GainRescale"][1/8, x], {x, 0, 1}]
Out[2]=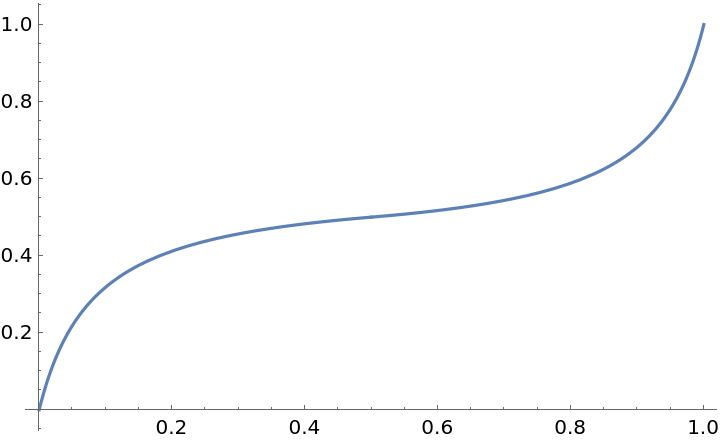

Plot different gain functions:

In[3]:=
Plot[Evaluate@ Table[ResourceFunction["GainRescale"][a, x], {a, {1/8, 1/2, 7/8}}], {x, 0, 1}, PlotLegends -> {1/8, 1/2, 7/8}]
Out[3]=

Scope (4) 

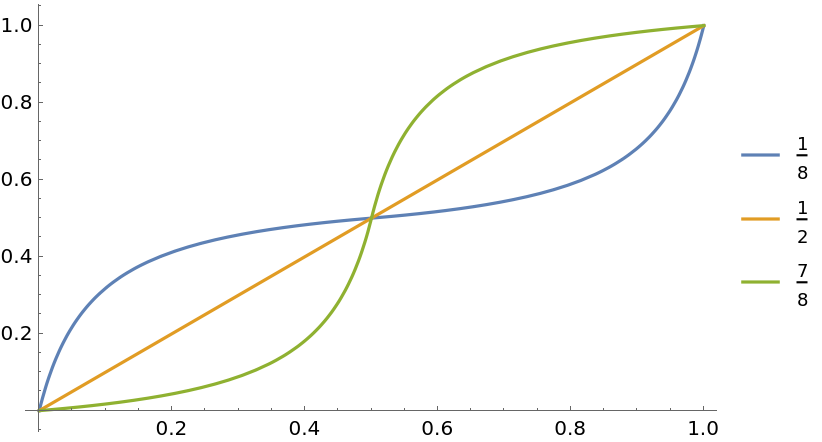Evaluate for symbolic x:

In[4]:=
ResourceFunction["GainRescale"][1/4, x]
Out[4]=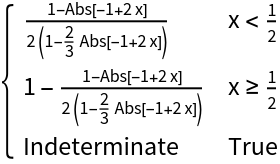

GainRescale threads over lists in its first and second arguments:

In[5]:=
ResourceFunction["GainRescale"][{1/8, 1/2, 7/8}, 0.3]
Out[5]=
In[6]:=
ResourceFunction["GainRescale"][7/8, {0.1, 0.3, 0.5}]
Out[6]=

Plot different gain functions with a rescaled domain:

In[7]:=
Plot[Evaluate@ Table[ResourceFunction["GainRescale"][a, x, {-1, 2}], {a, {1/8, 1/2, 7/8}}], {x, -1, 2}, PlotLegends -> {1/8, 1/2, 7/8}]
Out[7]=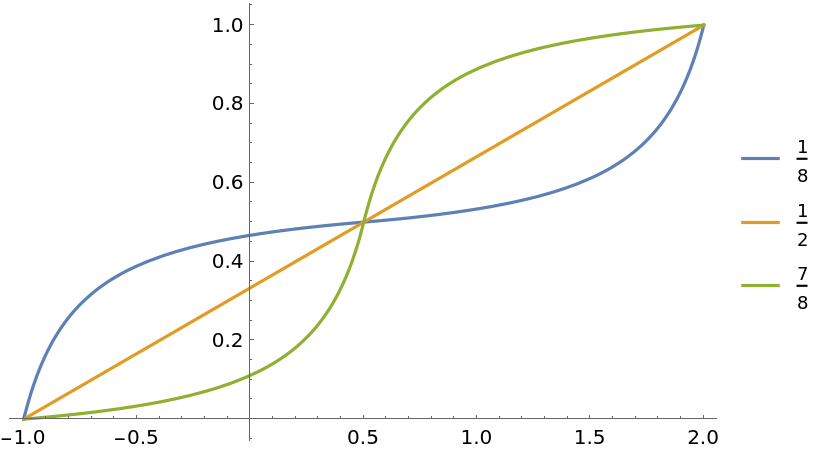

Plot different gain functions with a rescaled domain and range:

In[8]:=
Plot[Evaluate@ Table[ResourceFunction["GainRescale"][a, x, {-1, 2}, {-1, 1}], {a, {1/8, 1/2, 7/8}}], {x, -1, 2}, PlotLegends -> {1/8, 1/2, 7/8}]
Out[8]=

Options (1) 

Method (1) 

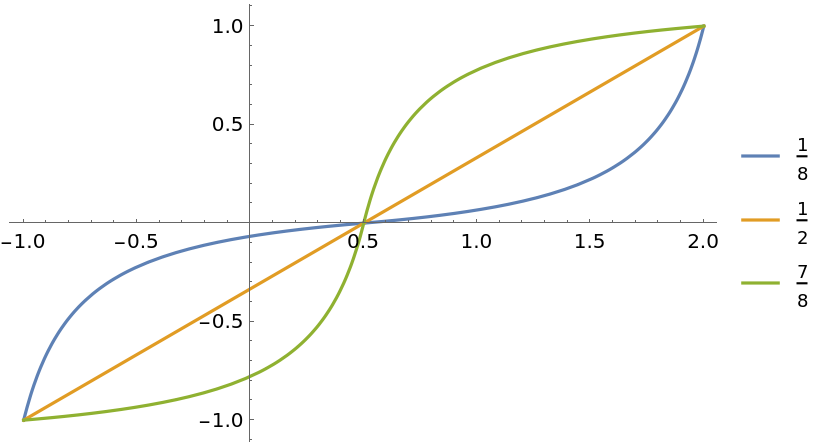Compare the Schlick and Perlin gain functions:

In[9]:=
{ResourceFunction["GainRescale"][3/4, x, Method -> "Schlick"], ResourceFunction["GainRescale"][3/4, x, Method -> "Perlin"]}
Out[9]=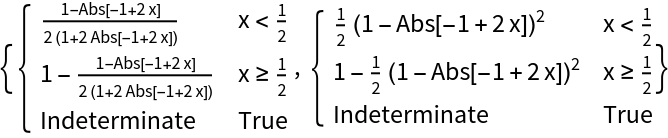
In[10]:=
Plot[{ResourceFunction["GainRescale"][3/4, x, Method -> "Schlick"], ResourceFunction["GainRescale"][3/4, x, Method -> "Perlin"]}, {x, 0, 1}, PlotLegends -> {"Schlick", "Perlin"}]
Out[10]=

Applications (2) 

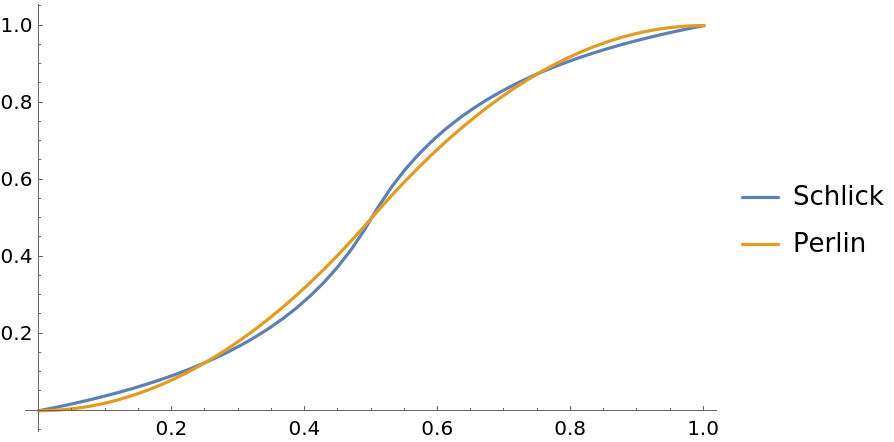Adjust the middle color of a built-in color gradient:

In[11]:=
Manipulate[ LinearGradientImage[ ColorData["ThermometerColors", ResourceFunction["GainRescale"][a, #]] &, {300, 30}], {{a, 1/2}, 0, 1}]
Out[11]=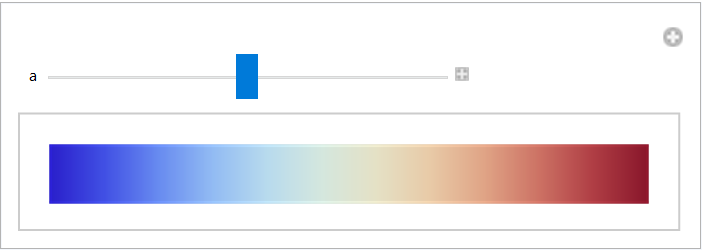

Demonstrate the effect of GainRescale on easing in/easing out:

In[12]:=
Manipulate[ Graphics[Text[ "Zoom!", {ResourceFunction["GainRescale"][a, x, {-1, 2}], 0}], PlotRange -> {{-0.1, 1.1}, {-0.1, 0.1}}], {{a, 1/2}, 0, 1}, {x, -1, 2, ControlType -> Animator, AnimationRunning -> False}]
Out[12]=

Properties and Relations (2) 

GainRescale[1/2,x,{min,max}] is equivalent to Rescale[x,{min,max}]:

In[13]:=
ResourceFunction["GainRescale"][1/2, x, {a, b}] == Rescale[x, {a, b}] // Simplify
Out[13]=

GainRescale[a,x] is a symmetrized version of the resource function BiasedRescale, made symmetric about x=1/2:

In[14]:=
With[{a = 1/4}, Plot[{ResourceFunction["GainRescale"][a, x], 1/2 \!\(\* TagBox[GridBox[{ {"\[Piecewise]", GridBox[{ { RowBox[{ RowBox[{"ResourceFunction", "[", "\"\<BiasedRescale\>\"", "]"}], "[", RowBox[{ RowBox[{"1", "-", "a"}], ",", RowBox[{"2", "x"}]}], "]"}], RowBox[{"x", "<", RowBox[{"1", "/", "2"}]}]}, { RowBox[{"1", "+", RowBox[{ RowBox[{"ResourceFunction", "[", "\"\<BiasedRescale\>\"", "]"}], "[", RowBox[{"a", ",", RowBox[{ RowBox[{"2", "x"}], "-", "1"}]}], "]"}]}], RowBox[{"x", ">", RowBox[{"1", "/", "2"}]}]} }, AllowedDimensions->{2, Automatic}, Editable->True, GridBoxAlignment->{"Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "ColumnsIndexed" -> {}, "Rows" -> {{1.}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.84]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}, Selectable->True]} }, GridBoxAlignment->{"Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "ColumnsIndexed" -> {}, "Rows" -> {{1.}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.35]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}], "Piecewise", DeleteWithContents->True, Editable->False, SelectWithContents->True, Selectable->False, StripWrapperBoxes->True]\)}, {x, 0, 1}, PlotStyle -> {Thick, Directive[Thick, Dashed]}]]
Out[14]=

Possible Issues (2) 

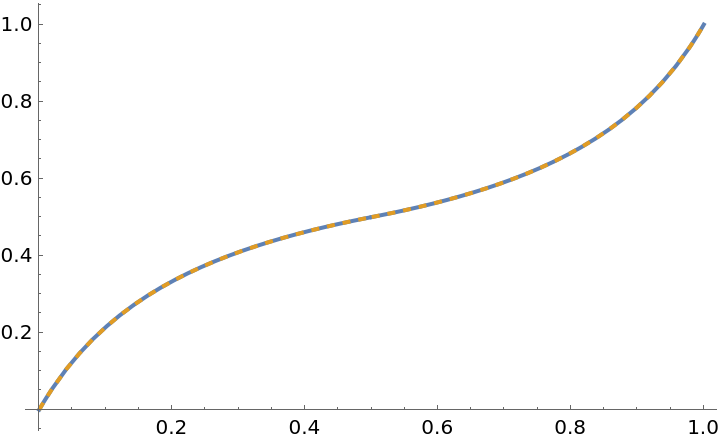GainRescale is left unevaluated if the first argument is nonnumeric:

In[15]:=
ResourceFunction["GainRescale"][a, x]
Out[15]=

GainRescale is left unevaluated if the first argument is not a real number between 0 and 1:

In[16]:=
ResourceFunction["GainRescale"][-1, x]
Out[16]=

Version History

  • 1.0.0 – 16 February 2021

Source Metadata

  • Citation:
    • Perlin K., Hoffert E.M., "Hypertexture." SIGGRAPH ‘89: Proceedings of the 16th annual conference on Computer graphics and interactive techniques, 253-262, 1989. DOI: 10.1145/74333.74359
    • Schlick C., "Fast alternatives to Perlin’s bias and gain functions." Graphics Gems IV, 401-403, 1994. DOI: 10.1016/B978-0-12-336156-1.50050-1

Related Resources

License Information