Compute the regions on which an expression is concave up or down
Contributed by:
Wolfram|Alpha Math Team
Examples
Basic Examples (2)
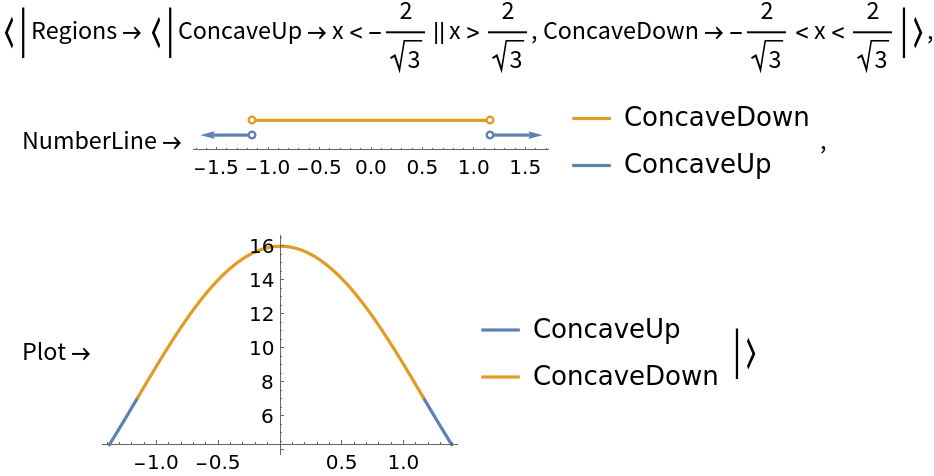
Compute the regions on which a curve is concave up or down:
Return plots as well as the regions:
Scope (4)
Use the "NumberLine" property to visualize the regions directly:
Use the "Plot" property to visualize the regions on the plot of the curve:
Note that at stationary points of the expression, the curve is neither concave up nor concave down. In this case, 0 is a member of neither of the regions:
To test that 0 is the only point where the second derivative is 0, use Resolve:
FunctionConcavity returns strict regions of the second derivative being non-zero as can be seen in this Piecewise expression:
Possible Issues (3)
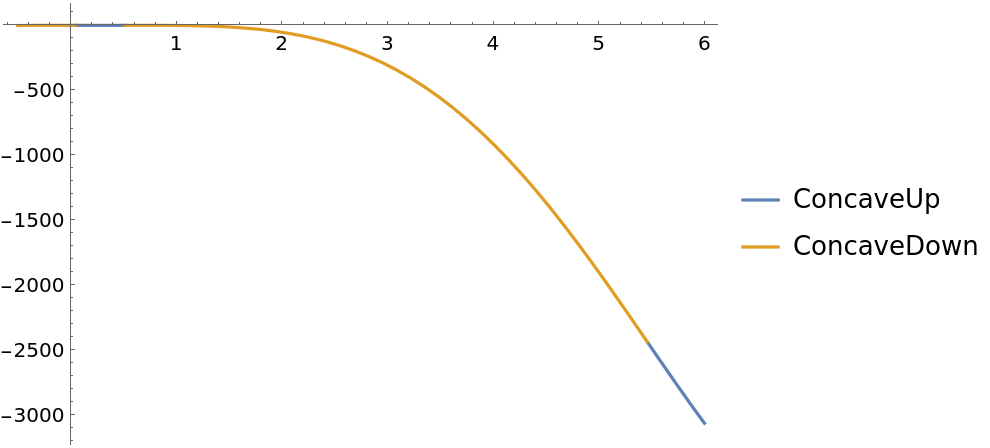
Working with the absolute value function Abs may return unexpected results:
This is due to the assumption of Complex inputs to Abs in comparison to RealAbs:
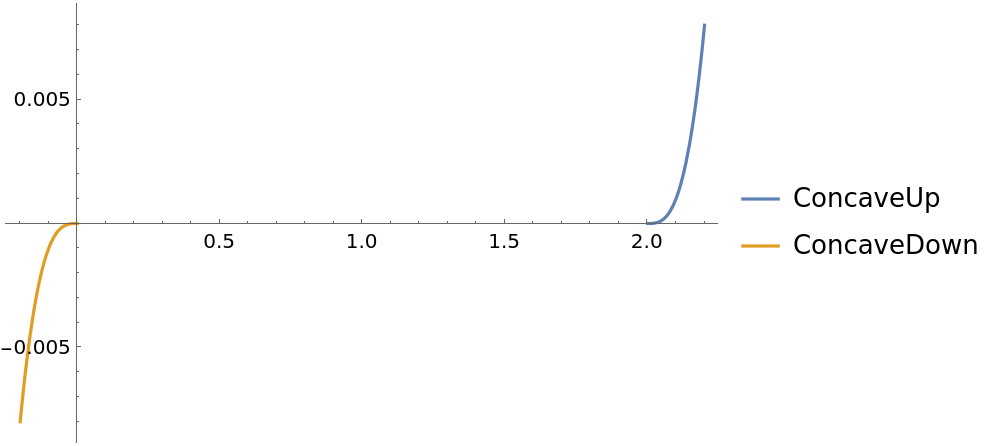
Using RealAbs returns the expected results:
Neat Examples (1)
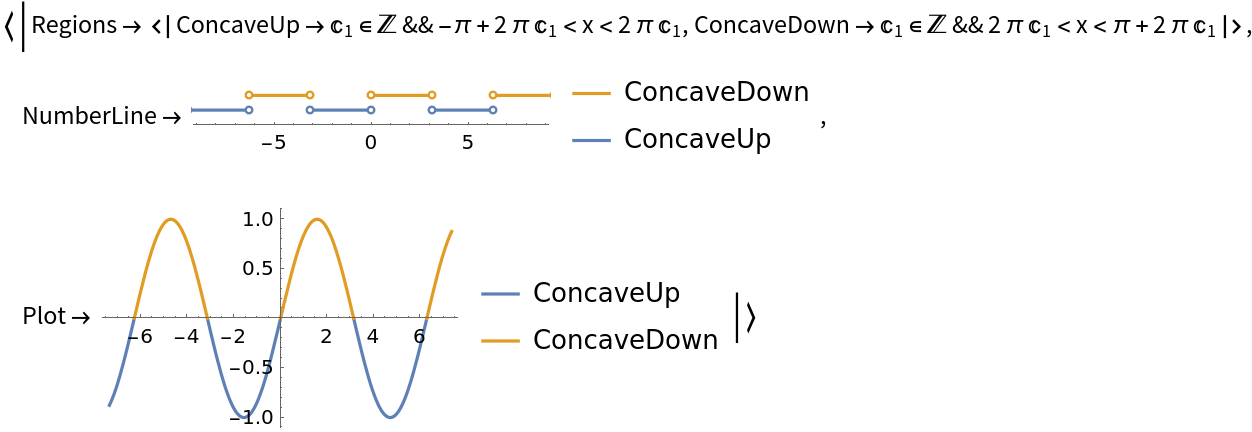
Compute the concavity of a periodic function and visualize it:
Publisher
Wolfram|Alpha Math Team
Version History
-
2.0.0
– 23 March 2023
-
1.0.0
– 18 September 2020
Related Resources
Author Notes
To view the full source code for FunctionConcavity, run the following code: