Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
An auxiliary function for the resource function FrobeniusPiecewiseDSolve
ResourceFunction["FrobeniusPiecewiseDSolveFormula"][eqn,u,x,x0] compute the formula for a piecewise Frobenius solution to a differential equation for the function u, with independent variable x. |
Compute the formula for a piecewise Frobenius solution to the ODE 7x(x+3)y'-3y=0 near the regular singular point x=0:
| In[1]:= |
| Out[1]= | 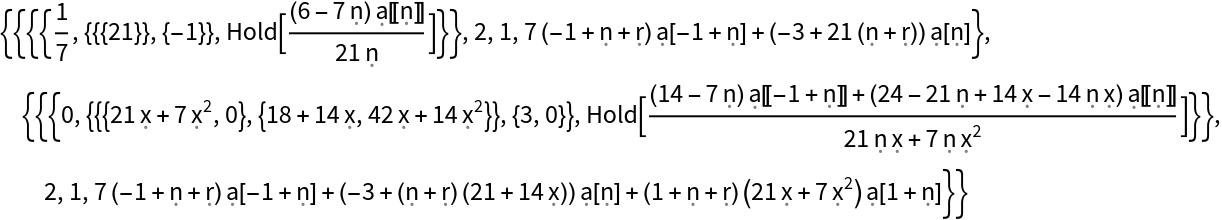 |
The function works with complex numbers:
| In[2]:= |
| Out[2]= | 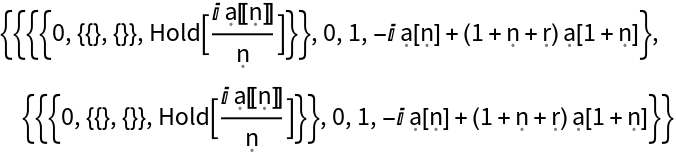 |
The resource function FrobeniusPiecewiseDSolve first computes a formula and then uses it to calculate the solution. FrobeniusPiecewiseDSolveFormula allows us to compute the formula separately, which can help significantly reduce computation time when an ODE is to be solved repeatedly:
| In[3]:= | ![Block[{eqn = (2 x^2 (x + 3)^2 y''[x] + 7 x (x + 3) y'[x] - 3 y[x] == 0), Xmin = 0, Xmax = 6, formula},
formula = ResourceFunction["FrobeniusPiecewiseDSolveFormula"][eqn, y, x, 0];
{
1000 First@
RepeatedTiming@
ResourceFunction["FrobeniusPiecewiseDSolve"][eqn, y, x, 0, {Xmin, Xmax}],
1000 First@
RepeatedTiming@
ResourceFunction["FrobeniusPiecewiseDSolve"][x, 0, {Xmin, Xmax}, formula]
}
]](https://www.wolframcloud.com/obj/resourcesystem/images/747/747285fe-5e56-4832-ac2a-1174087bd070/70f4be64e9b8d90b.png) |
| Out[3]= |
This work is licensed under a Creative Commons Attribution 4.0 International License