Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FourierShift

Source Notebook

Shift the zero-frequency term to the center of the spectrum

Contributed by: Yong-an Lu

ResourceFunction["FourierShift"][data]

rearranges a Fourier transform data by shifting the zero-frequency term to the center of the array.

ResourceFunction["FourierShift"][data,dim]

operates along the dimension dim of data.

Details and Options

In optics, the zero-frequency term appears in the center of spectrum.
For Fourier, the zero-frequency term appears at position 1 in the resulting list; ResourceFunction["FourierShift"] moves it to the middle.

Examples

Basic Examples (4) 

Swap the left and right halves of a vector:

In[1]:=
ResourceFunction["FourierShift"][{1, 2, 3, 4, 5, 6}]
Out[1]=

If a vector has an odd number of elements, then the shift moves the first element to the center:

In[2]:=
ResourceFunction["FourierShift"][{1, 2, 3, 4, 5, 6, 7}]
Out[2]=

Swap the first quadrant of the matrix with the third, and the second quadrant with the fourth:

In[3]:=
ResourceFunction["FourierShift"][\!\(\* TagBox[ RowBox[{"(", "", GridBox[{ {"1", "2", "3", "4"}, {"5", "6", "7", "8"}, {"9", "10", "11", "12"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\)] // MatrixForm
Out[3]=

Swap halves of each column of matrix:

In[4]:=
ResourceFunction["FourierShift"][\!\(\* TagBox[ RowBox[{"(", "", GridBox[{ {"1", "2", "3", "4"}, {"5", "6", "7", "8"}, {"9", "10", "11", "12"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\), 1] // MatrixForm
Out[4]=

Swap halves of each row instead:

In[5]:=
ResourceFunction["FourierShift"][\!\(\* TagBox[ RowBox[{"(", "", GridBox[{ {"1", "2", "3", "4"}, {"5", "6", "7", "8"}, {"9", "10", "11", "12"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\), 2] // MatrixForm
Out[5]=

Scope (2) 

FourierShift can be applied to a multidimensional array:

In[6]:=
ResourceFunction["FourierShift"][\!\(\* TagBox[ RowBox[{"(", "", GridBox[{ { RowBox[{"(", "", GridBox[{ {"1", "2"}, {"3", "4"}, {"5", "6"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], RowBox[{"(", "", GridBox[{ {"7", "8"}, {"9", "10"}, {"11", "12"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}]}, { RowBox[{"(", "", GridBox[{ {"13", "14"}, {"15", "16"}, {"17", "18"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], RowBox[{"(", "", GridBox[{ {"19", "20"}, {"21", "22"}, {"23", "24"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}]} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\)] // MatrixForm
Out[6]=

The dimension can be any valid part specification:

In[7]:=
ResourceFunction["FourierShift"][\!\(\* TagBox[ RowBox[{"(", "", GridBox[{ { RowBox[{"(", "", GridBox[{ {"1", "2"}, {"3", "4"}, {"5", "6"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], RowBox[{"(", "", GridBox[{ {"7", "8"}, {"9", "10"}, {"11", "12"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}]}, { RowBox[{"(", "", GridBox[{ {"13", "14"}, {"15", "16"}, {"17", "18"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], RowBox[{"(", "", GridBox[{ {"19", "20"}, {"21", "22"}, {"23", "24"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}]} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\), -2 ;;] // MatrixForm
Out[7]=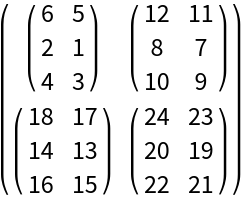
In[8]:=
ResourceFunction["FourierShift"][\!\(\* TagBox[ RowBox[{"(", "", GridBox[{ { RowBox[{"(", "", GridBox[{ {"1", "2"}, {"3", "4"}, {"5", "6"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], RowBox[{"(", "", GridBox[{ {"7", "8"}, {"9", "10"}, {"11", "12"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}]}, { RowBox[{"(", "", GridBox[{ {"13", "14"}, {"15", "16"}, {"17", "18"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], RowBox[{"(", "", GridBox[{ {"19", "20"}, {"21", "22"}, {"23", "24"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}]} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[ 0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\), {1, -1}] // MatrixForm
Out[8]=

Properties and Relations (2) 

For Fourier, the zero-frequency term appears at position 1 in the resulting list:

In[9]:=
spectrum = Fourier@DiskMatrix[16, 128]; MatrixPlot[Abs@spectrum]
Out[8]=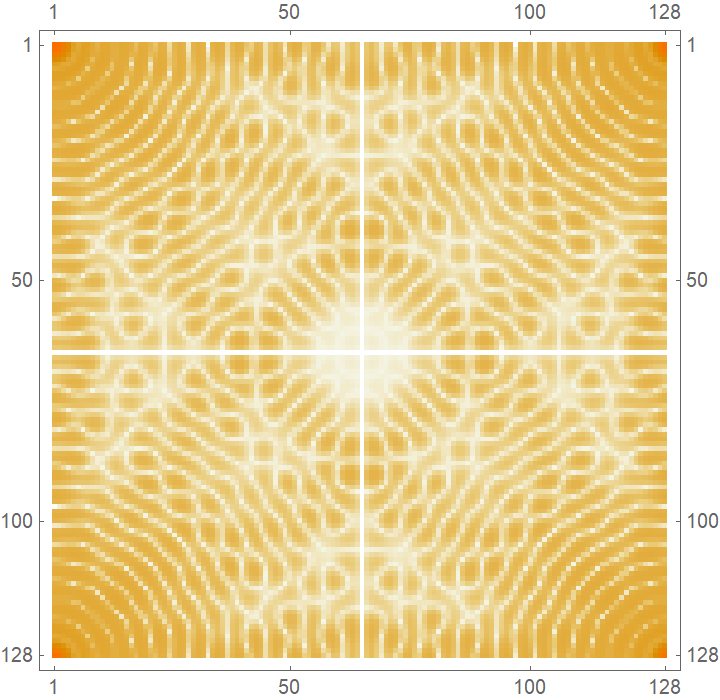

FourierShift shifts zero-frequency term to center of spectrum:

In[10]:=
MatrixPlot[Abs@ResourceFunction["FourierShift"]@spectrum]
Out[10]=

Possible Issues (2) 

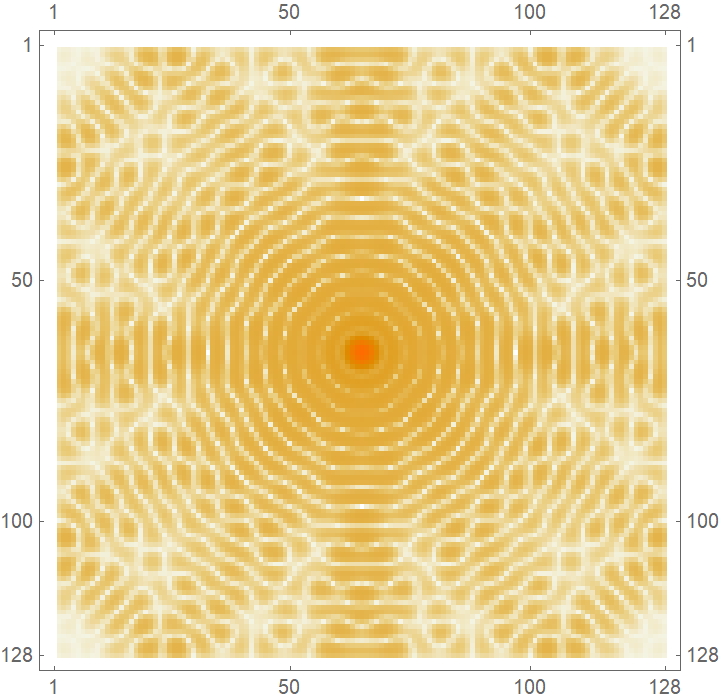FourierShift does not support ragged arrays:

In[11]:=
ResourceFunction["FourierShift"][{1, {2}, 3}]
Out[11]=

Calling FourierShift twice does not necessarily reconstruct the original input:

In[12]:=
ResourceFunction["FourierShift"]@ ResourceFunction["FourierShift"][{1, 2, 3, 4, 5, 6, 7}]
Out[12]=

Publisher

Yong-an Lu

Version History

  • 1.0.0 – 10 October 2019

Related Resources

License Information