Function Repository Resource:

FitPowerLaw

Source Notebook

Fit a power law to data

Contributed by: Sander Huisman

ResourceFunction["FitPowerLaw"][data]

fits data with a power law by fitting the log of data with a linear function.

ResourceFunction["FitPowerLaw"][data,x]

fits data and uses the variable x for the resulting fits.

Details and Options

ResourceFunction["FitPowerLaw"] effectively fits the function a x^b to the data, but does so by fitting the linear function c x+d to the log of the data.

ResourceFunction["FitPowerLaw"] fits in 'log space' such that fits that span multiple decades of data are not dominated by a few of the largest values and the smallest values are basically neglegible. The errors are therefore not in the sense of a classical least-square but rather the square of the log of the ratio of the fitted value and the original data. Visually this then results in a 'good fit' when the data is visualized in a log-log plot of the data.

The data data should either be a list of points {y₁, y₂, y₃, …,y_n} (to which the x coordinates 1 through n are assigned), or the data is {x,y} pairs: {{x₁,y₁},{x₂,y₂},…}, for a list of lists of data ResourceFunction["FitPowerLaw"] will fit each sublist, returning in that case a list of associations.

Only positive values are fitted. Negative points are ignored.

ResourceFunction["FitPowerLaw"] has the following options:

"Exponent"

Automatic

prescribe the exponent

"Prefactor"

Automatic

prescribe the prefactor

If both options are given, only the "Prefactor" option is used.

ResourceFunction["FitPowerLaw"] returns an Association with fit and fit parameters.

Examples

Basic Examples (1)

Create some data and fit it:

In[1]:=

$ResourceFunction["FitPowerLaw"][ Table[{i, 8.9 i^0.34}, {i, 10^Range[1, 4, 0.1]}]]$

Out[1]=

Scope (3)

For a single list of values the x coordinates are assumed to be 1,2,3,4…:

In[2]:=

Out[2]=

In[3]:=

Out[3]=

For a list of lists of data each list will be fitted separately:

In[4]:=

Out[4]=

For a list of pairs the data is assumed to be in {x,y} pairs:

In[5]:=

Out[5]=

Options (2)

Prescribe the exponent:

In[6]:=

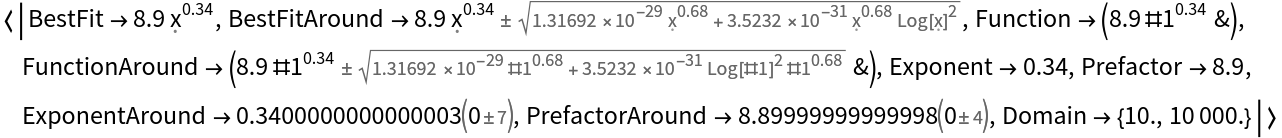
$SeedRandom[1234]; d = Table[{i, 14 (i RandomVariate[NormalDistribution[1, 0.1]])^0.5}, {i, 10^Range[1, 4, 0.01]}]; ResourceFunction["FitPowerLaw"][d, "Exponent" -> 1/2]$

Out[8]=

Prescribe the prefactor:

In[9]:=

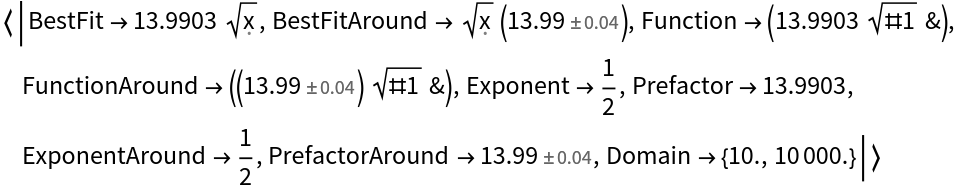
$SeedRandom[1234]; d = Table[{i, 8 (i RandomVariate[NormalDistribution[1, 0.1]])^0.312}, {i, 10^Range[1, 4, 0.01]}]; ResourceFunction["FitPowerLaw"][d, "Prefactor" -> 8]$

Out[10]=

Applications (1)

Create some data, fit it, and then plot both:

In[11]:=

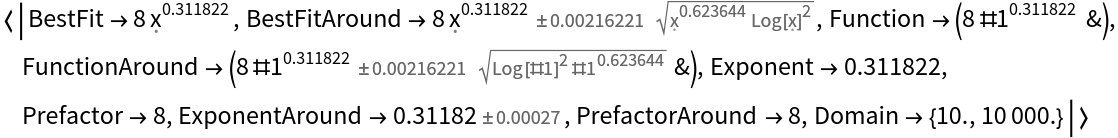
$SeedRandom[1234]; d = Table[{i, 8 (i RandomVariate[NormalDistribution[1, 0.2]])^0.312}, {i, 10^Range[1, 4, 0.01]}]; fit = ResourceFunction["FitPowerLaw"][d, x]; Show[{ListLogLogPlot[d], LogLogPlot[fit["BestFit"], {x, 10, 10000}, PlotStyle -> Red]}]$

Out[12]=

Possible Issues (3)

The difference between a classical least-squares fit or the fitting of the least-squares in log-space becomes very apparent when fitting over several decades. Because the error is much larger for the higher decades the error is completely dominated by those larger points, resulting in a strange fit when viewed in log-space:

In[13]:=

$d = CompressedData[" 1:eJwlV2c0EO7/tSojW0ZFlJW9hfB5HlllUyFlr2TvlVmZ2XsLiWRnZa8iIisj ykgpJKNvKv79z+++uee+u+fcF/deDgtnPWsiAgICQUICgv/n/4ETWNTvNBSd rYIGZ5SGvTmho7Hi4ajGc1BryTLQ2OIEMuMI/4BvRSASX/RS0IkLFmuvqn7b 7oAG+cZPP9e54GLrhv4h4WtQrlc59sKFGwjDFipdvzfBFhZai97jBrleqzDt kV5g1uFs8g3igfiLbnePm7RBZZgAeToFL2hFUHGcfVILxKlsi78yeSHm/m5f vXID3BeWa6gRPA9ddh3jRVcmwU5gxH2y+592lJlj1Z+E5vxvPr43+SCVPD6U 4PsMMPzmLKja5wMtjbfJIx86YLXYVikhix+iN4iRWcUYJEYuSoqCAFwWMdnu uLEMHuO/Rko+C0BVX7fISE07yDjr/CBNEYTNjqxUxvhhsH6weOikLAT25MsV jNOrUJol9vX7LyHYXZTWmri6ADY+kRKPa4ShqjekObpqAmoHOL0npEXAMiPf kaRxGk5y8n+ISheBI3ms80LLY9CU378b/FsEaHQMg79krAO9bRV3r5kolE2t FM5MbYD90zpR65ei8OYYSyO5zEfwM8jkcRYTAxKGNO682g2wqz7quJUrBjT2 hPWL/aOwW+z2Yp9SHEwpIy58T3oFbE58vJlB4vDp6vxO++QKOOkbnV7YFocl Md5OLi0iJJrMYT59WwKmvgSQ57T/APm+jtMZyxIQxnE62O3vN+g/7JgQMpcE ZdoAra2GDbCgk/Ys/yAJw+1E628zZoCXm0qd3VIKJq7bpgz9IkT9JOZH8z5L AXXDs6q1omU4Y/NxUMZVGuiEVrqrhSegJUGTk/ivNDzju7reI70NjOU7pFQx F6CCwmwjmnAJPA/Vlx3ZZKAiUkDCunYbMisfJEvVyUCL8UOFvvd/gYTG3ClA UxZcg9sLCk/vgw1br6LBmizsb11kYr6wA5cdqvXGouTArMrcqmlrEl7MnHCh Fr4IVR9tr08o06M/ea8W2aYuwpcU5m8kXzaBYTbBjzlMHnw/1q9eC+NG95Fs HL24ApDvHZYcEyFGcfIdxLyrCsDSwvFd7j9yxPMjXt0pTxFcOkJYT3LvgsTl 9epDQYDlCwE8x9IZ0Zs+H0+/hwC69iZlRJkk6M/68gOJLYDZ2kfZeIUMGaR0 actdQxApPZ3ILE2PbKmiw7JbEdRmicmt6DKilaIAfhseDNUMWanHzq8ArVTo o5IkDBPaDzbvLNCgznPcOXeIlKDmp8cNh2EOFP8pnqPfXQnWGGfHKo2Po4rw pKTeVSUQ/p1Ge3tXBP0Qb6v2vnUJ3pQ49qVYEiFtl7D09alLMJlcJ1wscAYx jdj2SBsow9FbX1bnRnnRkSUFBtsxZbhXal/LNMiCRuw8B2OuqsDDdTKz3A9C aFTYPrl5RgXIQn6ZfS4VQ7LfhkOJLFVBprTRPiheHNGZcDN6b6iC2RmL5Lvz YsjiuPxF/kA1ODzz4MHtHUlUxNShL0atDhUCHjI/3vGjJcn3QvlF6iCiZBlW 7cCFBv22T0TKX4YnieNk/mpSSIPNYIBw5jIIzx5OszOdQ6xV9JFn/K7A/Fpz 4d8ycVTJ9I3yP1YNOKVaVae1z4/e9QinFvRqwFE+DbGn6SLomffwkpirJkhu 2TIsEV1EQaR3oJtdC2h/O9+QIxJAElmRwbfHtaBrOLqO9Yk8+lPeeRTFaMPo JOXbhWJxNFITvSTMqQMHE69osIAcghkBLpdwHZhrqFy7P6aB/igPGW580oGH Bad6fGNVEHJ4P9dwRRf2San/BpRhdKTvnulMjS68WzKVUqiQQGRSoR8sT+vB 4bzB34ohC/TKibTWIkIPvh4KCC9R6KLnLU1BK3t6MKrCQifJoIcOTPJVftvq Q+si73XTdRmk1nnBvHZWH1JikmfqPRXQ4tL9cFY9A5iZ5jml/voaOs50oVt9 0ACIrPy9WIt0EN+90Tg11auQoaAwGbBvhP6r/drG13cVxjV/a93RwojS0D+S UO0arIeM3qNMu4m0+3ni5l9fA3+b45fOhmGkbVL5bszgOqwpmo8K5JkjElbj me2F68CVMNQfgC4j930/L10nQ8h7wzksZKCH/tcfRpC/Ecw9eaiCCgZp5elT jGDgwZUTWczm6GRZl32eoDHsnrO7ZbJngxTrhmSbXhkDXRtxHH+rK+LUtPng aX8DgoL5z03taaNEC2ayr8dNYEomsPM7VQCqGGtaFqozAVWv65GBVpborJUj j6HpTVA6X8o3peaBsooajt+lugWMOYenCu6boyC5EuPGzlswJ65o/XHMDdn9 JrM+42sKi4tWGwH1Sqj7lAWpzUkz8PbyBvFTbMhjOemrg58ZTH49mXL6qTv6 drrB6tmcGQRwLe/QPrdGVf3sA7LIHGLs3URiqc0RQWpFJ1upOShYU+sRaLmi Qc5sbEdrAY+LNww23WxRuLJbGlegBcSWmhKSutmg7OR1U+uvFuDydDa6AOki 9YLDRCkTS2h/s+glZOSDlL5OBJe+sYRgq/JGZ9tAZPZ3fXxA2QrMt5/aH/j5 IdZ1yfSKNivAknvy5FKxaDVCRtxc1hoyFNsCKafd0WywicteozVwTZ1mHrZM QGFTHHfvytqA2DfiqrMnQlHql+At8nYbaO48S1hBF4I6b6q9rFCxBe7Q+cq7 UunISzvOwXfUFsaMG4KlZ1JQCZlkTbCpHSy9tJ4imAtHKqXOS5Pf7aCAKDSZ vMEVyf+yb4q7Zw8h77mE4/P90cjP75btrLfhXeVcplVSGWpSFI32a7oNLiPx /d9dY9DeZLjepKEDqJtKRH0JC0M1lbo3Pv/+p3tFjkSGxSNClV/9fYV3IP7b 9CRhhD163D6tEKHpCFyHX3FObhQ6v2e2rvTHEcK7ujb99iPQ7IRoNG2lExhl UzZ9GfVEJkEmN8lsnCHTqJZini4WdQyNny6kcQFJLsMCn5FkRFz2p8fRxQWa vjwhIMkqQ3/FZh97vHUBkB0JU3IpQFRLz+h7pFzh9a7PeZq4fNRYSllin+MK nEK1xz6K1KC/xG2a7kfd4I6Hi9/wu0K0xpulsenqBrqJ5mY7VAVoxy5c5tuC G1AwkmyHsVajAG5DIl8dd7gZ2EVOvFWNjNL214u63aG7bZIiezATtWXb5QbJ eIDGpvDbg50KFPrfJB1LjQccn7pxuochCgWdn38SIugJ/Oz9cTNVleiJbO25 gXJPUKLmKzwR2ogORh2LiAW9QFtDiZ9x+BFiG77xXLHaC3ijXxemh3Sg9G4L jfgL3jAz8pT7BPsoqnnq3HOs2xtC8jyvW4lWIgn23S+NOj5A4jyp/+5OGXpn 7fPf848+YEHjq5hJ0Yv2OgRzT3j5Au+t6C84pxhZaBQdfKb0g/dYcUjCaxyx 9oTUKz/xA2Ne0olBpXbUl6U1DWr+cGCk/4qEvRkd79Y72Fzzh8zOgcDJqdeo zz9Mxj4hALgk38W5WPYh9ceh57rlAoFCIXv83eoAotqunGVYC4QiPorr5DNr yF9bg8Ir+y5MkzHkLhMMoxjWqs8HekHwUGw652rtInqGLrMuHw2GUPvE5Trz DvRCoLHC0yYYBJLvbw0njqHNRA829DIYrPSoyiVLFhCD1tN6fYEQMMht0Lzw thUNPawlbUkMgW+VEoZ/ll8iktn3f8N/h0CmUpghcn+DhsjNh9ttQuGK9G50 9s4i0runROo3HgqXVHpHjI2GEQHhtfiuS2Ew8nPra77FIvKnkCkqbQiDS2ax LdR5DSg8z2lOTjAcXkfQVsWubKAxGh+hmOJwOHHxo9SsUS/yTyPYfMJ+Dxri h8JCiOsRbR/DeHHuPehgOk88sLaF7kvb/ow/cx9SpQP1WmrXUGJ34buAR/ch YILiHUPtKvKPGjD153sA7SkKUc5aH9AjvtKF3LoHUNB262au2TiS91Bj3kcR YDzDqaWQtY0Ktu7L5L+NAHPO267jk3toNrt0pcgmEiSVE+a8Fonxm9NHJU4f RILhYI8nic4mcvzUW3syIwpM9C7nmWvvob38Eqd66WjI+OWbw/N5AdEIzXwl nIkGkR0dHoe0NXS2aUuMMTgGnJwZ+3olltAt8dlhUr5YUN0Q3Z1rPYZVir6P fJ+Khfzrz/nv9v/Lo4llfCXyIfSHpnYPde78rz8gDpgrmGZIRPZRksK144b7 cUC6qe/gQTCJdMpYCsNM4oFL50fQ4/QjuDS+o4e+LR5IWJZVD5s+IOnvik+/ cCSAgswPNiVOKpwlX7lCF5EAqRWv51epabAG545WzvcEGH755r8e0+M4/lYR c9qNRKglnml+KU6MP/b96Kd6lQgZRdqrki/psfDK4wv0Mklw6UEEUwHFUcwh /292lydB6ODSaBAZG35W6Bd1yJ4MMsp7ca+/baPE9z6fjmYkww1pfFbCZBfx LC//naZPgXZjr9gkurM4+1dpQGRCCtQNF4hwctFiv9/Mbtx0qSC2Ljdjeucs PhBU0u9KSQUd+auO1tGn8Mqk1l+n02lAGX3VYE/4FB749blBoSQNjkj5yAfV n8BZke3Sl8TTQSApl6XkPQOmt6EoSOxOh0nh2NyIIRrcGHA+Sv56BoQk3xaJ WWfEd+yUDgw3MmBS6tDdpJUas389FvwrIhNC+t+Z3U7iw3QF7scleLKguarB ffLiOWylWcbK9ioLfEwviv+6eBYTc36sGHLKBgI/yy06bQYs5mksa8ScA6nU IFnsy4n1z7n3TfXmwPaRQfYN3XOYWqNr3sw7F4Z65+7spDBh88Qr2ccF8+B9 bSt7CLc8jvHuebz9KQ+0qxwpbjucwfOZXrlpevngY/W4TiZDCo/3H6R+q82H q80P2XM9eLHx0aTte0wF0HJ4QNR7C+E3lPQyroEFQL5Y9nzBQBS/GPx98cVK Aaicfz5x/+dl/IpJjcdTpxBauPdftz1SwTMZJh5lrYVQ48yWvJkP+AnX4d5t wUegv9csyazPjpPfGM305j0Czoi7rSHiYliEkLxogKEIouXO2Vr9xThsXE4q MqYIKmfnds6UY9x1ODpKe6z4389ZlJGgVsVvszKZPcOLQem0k4BdmST+RJdA 3UNSAuraPdz9XQb4b7ggB01ECURJHVnOF9fA/NudZxyoHoPOyhsy51MXsWjY iupq2mMYVZS3Ku6Rx6dENnAaZynMXfLhaUtFWFje9/zDulJgMJx6qZaN8G43 0f0F1SeAFTMvWzJcw4+ex1zPm38C68ZkXLbFoni+9irDok8ZJAwtbG6c18QG ZPlPXzCWAx9dcayAnwW+pxIZe6mxHBxDd8ujvmjh4s4fj+JuPoUvPtc8BISu Yy8Pf9O6oxVgMTrVOXZODc+nRde/qq2A8rYcz9xAXYzs3DhXrZ5BiTrjqYpC a6wVlPqc82Ql/IifPGbVboX5RZuOZI1Vgt21g1FNQh3cWsmdV61WBX3Pj0Wf fWOJE0+6Jgw+qYIXt2j4Lk3ZYhOO0Qe8lNX/9uMHq1BeB7zUtH0w4VYN4jI3 hZ14vPENwR/dH2eqwXGcZiRlyhLHloruGSnXQGINPUtBkB/e+KlJpllTA6o9 KVi2PxxXVFP3v+KoBRlxp9ebYXbYh85JdyGpFuDTUkeapTtmeZvNmUNaB+8V xfSbxhzwljQ3C31wHfCMX2Bwz7fB5Q20Nrr7dbBbWvD5qawlzjRnemTnXQ9x /Z/wxClDHOL2YcD+Zz2M8BRpJOs549e6V+Vt/J4Dd7DQ0ScsVjhY81enM0ED RDhent+vt8YlNgZR6ZEN0NXCo8or54tRiIPE9olGeLZGm/a12guba6kOJRY3 AvnPlYPCKTdsrRo1FnWhCaI+M1Ht2sdighOMspvDTZDm3M/Fs2qLjVo7bo/b NYNSHaGVYqAHTvnJoq59tAXuVBcWcr1IxXZHkKTn4xbYOQulndoJ2MljkMpE 4wX45Pyu3d2PxCcFW6VP7r6A8pbe8y7R2VhDMjGtr6AV3MIWOUwoYrFGgnGu j14btFudS/exTsYEzz6rqh1rh17l4R9/9IMwbQ/dGa2OdkjjnG869iIGE70N yx9V6IDmD88utR4GYrKqG1VVeR1A5dIc5Bt/H2dy8lqPEnVC3PePUVO0aXjA xE4c2XWCQmBX0jX+UFxPP7VAOdIJe82+O9cXYjE7gXqIsmwXTEsQjlwhjcdP bVJD90q6oJDRrMObJQdX0McXCTN2g71Ci/5743/+/h8R3TA3Ncp9TSca/x8y ZMR1 "]; 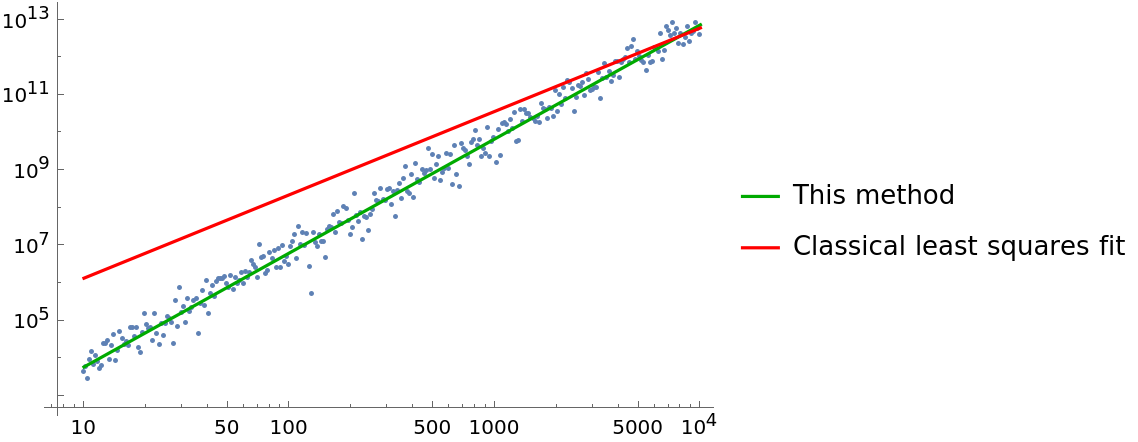fit = ResourceFunction["FitPowerLaw"][d, x]; fm = NonlinearModelFit[d, a x^b, {a, b}, x]; Show[{ListLogLogPlot[d, PlotRange -> All], LogLogPlot[{fit["BestFit"], fm["BestFit"]}, {x, 10, 10000}, Sequence[PlotStyle -> { Darker[Green], Red}, PlotLegends -> {"This method", "Classical least squares fit"}]]}]$