Details
A mask is a rectangular array containing only zeroes and ones.
A template is a rectangular array containing non-negative integers or
Blank (_) values.
A complete set of binary templates follows from a mask by turning 0's into blanks, 1's into independent slots, and then filling the slots with 1's and 0's in all possible ways.
Similarly, a complete set of c-color templates follows by filling the mask slots with all possible Tuples of the numbers 0,1, …, c-1, where of course c is a positive integer.
A template is mask-consistent if it belongs to the complete c-color set derived from mask.
Sets of potentially many templates should have the same bounding size, say {a,b}, and they certainly do if derived from a single mask of bounding size {a,b}.
A tiling pattern is any rectangular array of non-negative integers.
If all {a,b} subarrays of an {m,n} pattern match a template from input templates, the tiling pattern is said to be "consistent with local constraints listed in templates", or for short, "template consistent".
By "minimal" we mean that any found subset of templates can not be reduced by removing a single templates without making it impossible to form a tiling pattern of size s.
There are two methods to search for minimal sets. One is to start with cardinality n subsets and, for positive results, check reducibility to cardinality n-1 subsets. The other is to perform a breadth-first search of increasingly large subsets up to n cardinality. This resource switches between methods automatically according to coverage.
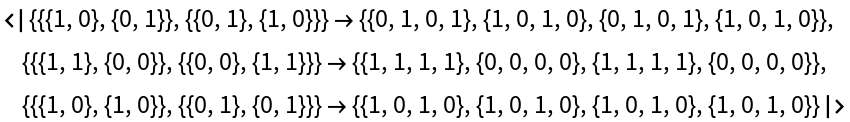
![With[{res = ResourceFunction["FindMinimalTilings"][{
{1, 1}, {1, 1}}, 2, 4]},
Row[KeyValueMap[Labeled[ArrayPlot[#2,
PixelConstrained -> 20],
Row[ArrayPlot[#, PixelConstrained -> 10
] & /@ #1, Spacer[2]]
] &, res], Spacer[10]]]](https://www.wolframcloud.com/obj/resourcesystem/images/2ca/2cadf91c-242c-4d7c-941c-514349ebbea1/4ce307ec35d8f528.png)

![With[{res = ResourceFunction["FindMinimalTilings"][{
{1, 1, 0}, {0, 1, 1}}, 2, 4]},
Row[KeyValueMap[Labeled[ArrayPlot[#2,
PixelConstrained -> 20],
Row[ArrayPlot[#, PixelConstrained -> 10
] & /@ #1, Spacer[2]]
] &, res], Spacer[10]]]](https://www.wolframcloud.com/obj/resourcesystem/images/2ca/2cadf91c-242c-4d7c-941c-514349ebbea1/6fcf6630f88196e4.png)


![With[{res = ResourceFunction["FindMinimalTilings"][{
{1, 1}, {1, 1}}, 3, 4, 3]},
Grid[Partition[KeyValueMap[
Labeled[ArrayPlot[#2,
ColorRules -> {0 -> Red, 1 -> Green, 2 -> Blue},
PixelConstrained -> 20],
Row[ArrayPlot[#,
ColorRules -> {0 -> Red, 1 -> Green, 2 -> Blue},
PixelConstrained -> 8
] & /@ #1, Spacer[2]]
] &, res], 4], Spacings -> {2, 1}]]](https://www.wolframcloud.com/obj/resourcesystem/images/2ca/2cadf91c-242c-4d7c-941c-514349ebbea1/1c6b147529580437.png)

![With[{res = ResourceFunction["FindMinimalTilings"][{
{1, 1}, {1, 1}}, 2, {4, 6}]},
Row[KeyValueMap[Labeled[ArrayPlot[#2,
PixelConstrained -> 20],
Row[ArrayPlot[#, PixelConstrained -> 10
] & /@ #1, Spacer[2]]
] &, res], Spacer[10]]]](https://www.wolframcloud.com/obj/resourcesystem/images/2ca/2cadf91c-242c-4d7c-941c-514349ebbea1/13c4cca943e56eda.png)

![With[{res = ResourceFunction["FindMinimalTilings"][{
{1, 1}, {1, 1}}, 2, {4, 6}, {{1, 0}}]},
Row[KeyValueMap[Labeled[ArrayPlot[#2,
PixelConstrained -> 20],
Row[ArrayPlot[#, PixelConstrained -> 10
] & /@ #1, Spacer[2]]
] &, res], Spacer[10]]]](https://www.wolframcloud.com/obj/resourcesystem/images/2ca/2cadf91c-242c-4d7c-941c-514349ebbea1/7a5b7c6916c06af6.png)

![With[{res = ResourceFunction["FindMinimalTilings"][
Partition[#, 2] & /@ Tuples[{0, 1}, 4], 2, 4]},
Row[KeyValueMap[Labeled[ArrayPlot[#2,
PixelConstrained -> 20],
Row[ArrayPlot[#, PixelConstrained -> 10
] & /@ #1, Spacer[2]]
] &, res], Spacer[10]]]](https://www.wolframcloud.com/obj/resourcesystem/images/2ca/2cadf91c-242c-4d7c-941c-514349ebbea1/775fa4a46d97fcd0.png)

![With[{tileset = {
{{_, _, 1}, {1, _, 0}, {_, 0, 0}}, {{_, _, 1}, {0, _, 1}, {_, 0, 0}}, {{_, _, 1}, {1, _, 0}, {_, 1, 0}}, {{_, _, 0}, {0, _, 1}, {_, 1, 0}}, {{_, _, 1}, {1, _, 1}, {_, 1, 0}}, {{_, _, 0}, {1, _, 0}, {_, 0, 1}}, {{_, _, 1}, {1, _, 1}, {_, 0, 1}}, {{_, _, 0}, {0, _, 0}, {_, 1, 1}}, {{_, _, 1}, {0, _, 0}, {_, 1, 1}}, {{_, _, 1}, {1, _, 0}, {_, 1, 1}}, {{_, _, 1}, {0, _, 1}, {_, 1, 1}}, {{_, _, 0}, {1, _, 1}, {_, 1, 1}}}}, ResourceFunction["FindMinimalTilings"][tileset, 11, 20]]](https://www.wolframcloud.com/obj/resourcesystem/images/2ca/2cadf91c-242c-4d7c-941c-514349ebbea1/7d592906b5484b1d.png)
![AbsoluteTiming@With[{tileset = {
{{_, _, 1}, {1, _, 0}, {_, 0, 0}}, {{_, _, 1}, {0, _, 1}, {_, 0, 0}}, {{_, _, 1}, {1, _, 0}, {_, 1, 0}}, {{_, _, 0}, {0, _, 1}, {_, 1, 0}}, {{_, _, 1}, {1, _, 1}, {_, 1, 0}}, {{_, _, 0}, {1, _, 0}, {_, 0, 1}}, {{_, _, 1}, {1, _, 1}, {_, 0, 1}}, {{_, _, 0}, {0, _, 0}, {_, 1, 1}}, {{_, _, 1}, {0, _, 0}, {_, 1, 1}}, {{_, _, 1}, {1, _, 0}, {_, 1, 1}}, {{_, _, 1}, {0, _, 1}, {_, 1, 1}}, {{_, _, 0}, {1, _, 1}, {_, 1, 1}}}},
ArrayPlot[
Last[Last[
Normal[ResourceFunction["FindMinimalTilings"][tileset, 12, 20]]]]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/2ca/2cadf91c-242c-4d7c-941c-514349ebbea1/6104a2f8888cdb74.png)

![AbsoluteTiming@With[{tiles = {{{
Blank[], 1,
Blank[]}, {1, 0, 0}, {
Blank[], 0,
Blank[]}}, {{
Blank[], 1,
Blank[]}, {0, 1, 0}, {
Blank[], 0,
Blank[]}}, {{
Blank[], 1,
Blank[]}, {0, 0, 1}, {
Blank[], 1,
Blank[]}}, {{
Blank[], 1,
Blank[]}, {0, 0, 1}, {
Blank[], 0,
Blank[]}}, {{
Blank[], 1,
Blank[]}, {0, 0, 0}, {
Blank[], 1,
Blank[]}}, {{
Blank[], 0,
Blank[]}, {1, 1, 1}, {
Blank[], 0,
Blank[]}}, {{
Blank[], 0,
Blank[]}, {1, 0, 1}, {
Blank[], 1,
Blank[]}}, {{
Blank[], 0,
Blank[]}, {1, 0, 0}, {
Blank[], 1,
Blank[]}}, {{
Blank[], 0,
Blank[]}, {0, 1, 1}, {
Blank[], 1,
Blank[]}}, {{
Blank[], 0,
Blank[]}, {0, 1, 0}, {
Blank[], 0,
Blank[]}}, {{
Blank[], 0,
Blank[]}, {0, 0, 1}, {
Blank[], 0,
Blank[]}}, {{
Blank[], 0,
Blank[]}, {0, 0, 0}, {
Blank[], 0,
Blank[]}}}},
ArrayPlot[Last[Last[Normal[
ResourceFunction["FindMinimalTilings"][tiles, 12, 16, {{1}, {1}}]
]]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/2ca/2cadf91c-242c-4d7c-941c-514349ebbea1/5a0bdf64a791ef3b.png)
