Function Repository Resource:

ExpectedClassifierMeasurements

Computes an expectation of classifier measurements over a probability distribution of utility functions

Contributed by: Seth J. Chandler

ResourceFunction["ExpectedClassifierMeasurements"][classifier,testset,{probs₁,…probs_n}→{u₁,…,u_n}, prop]

gives the expected measurements for property prop when classifier is evaluated on testset and utility functions u_i, determining how an example is classified, are chosen from distributions with corresponding probabilities probs_i.

ResourceFunction["ExpectedClassifierMeasurements"][classifier,testset,{probs₁,probs₂,…probs_n}→{u₁,u₂,…,u_n},{prop₁,prop₂,…}]

gives the expected measurements for properties prop_i.

ResourceFunction["ExpectedClassifierMeasurements"][classifier,testset,dist,prop]

specifies the probability distribution directly as any form of DataDistribution.

Details and Options

Properties of ResourceFunction["ExpectedClassifierMeasurements"] are a subset of those of ClassifierMeasurements.

Properties of ClassifierMeasurements that return Graphics objects ("Report", "ROCCurve", "ProbabilityHistogram" and "AccuracyRejectionPlot") are not available for use with ResourceFunction["ExpectedClassifierMeasurements"].

Properties of ClassifierMeasurements that return examples are not available for use with ResourceFunction["ExpectedClassifierMeasurements"].

One cannot use this function to generate a ClassifierMeasurementsObject.

The options for this function are the same as for ClassifierMeasurements, though use of the UtilityFunction option will be ignored.

When the third argument is given as a DataDistribution, it can take several forms, such as an EmpiricalDistribution.

Examples

Basic Examples (6)

Get training data on the Titanic:

In[1]:=

Out[1]=

Get test data:

In[2]:=

Out[2]=

Build a classifier:

In[3]:=

Out[3]=

Develop two different utility functions:

In[4]:=

utilities = { <|
"died" -> <|"died" -> 0, "survived" -> -1|>, "survived" -> <|"died" -> -1, "survived" -> 0|>
|>, <| "died" -> <|"died" -> 0, "survived" -> -10|>, "survived" -> <|"died" -> -1, "survived" -> 0|>
|> };

Compute the expected confusion matrix:

In[5]:=

Out[5]=

Compute the expected "F1Score" and "CohenKappa" measure:

In[6]:=

Out[6]=

Scope (5)

Get training and test data on the Titanic and generate a classifier:

Develop two different utility functions:

In[7]:=

Use rules rather than a type of DataDistribution to represent the distribution of utility functions:

In[8]:=

Out[8]=

Use a symbolic distribution of utilities:

In[9]:=

Out[9]=

The function works with more than two utility functions:

In[10]:=

ResourceFunction[
"ExpectedClassifierMeasurements"][c, titanicTest, {0.5, 0.4, 0.1} -> Append[utilities, <|"died" -> <|"died" -> 0, "survived" -> -0.5`|>, "survived" -> <|"died" -> -1, "survived" -> 0|>|>], {"ConfusionMatrix", "F1Score", "CohenKappa"}]

Out[10]=

Options (5)

Get training and test data on the Titanic, generate a classifier and create utility functions:

You can use weighted data by employing the Weights option:

In[11]:=

With[{weights = RandomReal[{}, Length[titanicTest]]}, ResourceFunction["ExpectedClassifierMeasurements"][c, titanicTest, {0.2, 0.8} -> utilities, {"ConfusionMatrix", "F1Score",
"CohenKappa"}, Weights -> weights]]

Out[11]=

It will compute uncertainty where appropriate when the ComputeUncertainty option is set to True:

In[12]:=

(SeedRandom[1234]; With[{weights = RandomReal[{}, Length[titanicTest]]}, ResourceFunction["ExpectedClassifierMeasurements"][c, titanicTest, {0.2, 0.8} -> utilities, {"ConfusionMatrix", "F1Score", "CohenKappa"}, ComputeUncertainty -> True]])

Out[12]=

It will work with an indeterminacy threshold if the IndeterminateThreshold option is used:

In[13]:=

Out[13]=

It will work with class priors if the ClassPriors option is used:

In[14]:=

ResourceFunction[
"ExpectedClassifierMeasurements"][c, titanicTest, {0.2, 0.8} -> utilities, {"ConfusionMatrix", "F1Score", "CohenKappa"}, ClassPriors -> Association["died" -> 0.9, "survived" -> 0.1]]

Out[14]=

Applications (3)

Get training and test data on the Titanic and generate a classifier:

In[15]:=

(titanicTraining = ExampleData[{"MachineLearning", "Titanic"}, "TrainingData"]);
(titanicTest = ExampleData[{"MachineLearning", "Titanic"}, "TestData"]);
c = Classify[titanicTraining, PerformanceGoal -> "TrainingSpeed"];

Plot the possible combinations of false positive rates and true positive rates as the weight placed on the second of two utility functions goes from 0 to 1:

In[16]:=

$With[{\[Gamma] = Query[Values, "survived"][ ResourceFunction["ExpectedClassifierMeasurements"][c, titanicTest, {w, 1 - w} -> { <| "died" -> <|"died" -> 0, "survived" -> -1|>, "survived" -> <|"died" -> -1, "survived" -> 0|> |>, <| "died" -> <|"died" -> 0, "survived" -> -3|>, "survived" -> <|"died" -> -1, "survived" -> 0|> |> }, {"FalsePositiveRate", "TruePositiveRate"}]]}, ParametricPlot[\[Gamma], {w, 0, 1}, AspectRatio -> 1, Frame -> True, FrameLabel -> {"FPR", "TPR"}] ]$

Out[16]=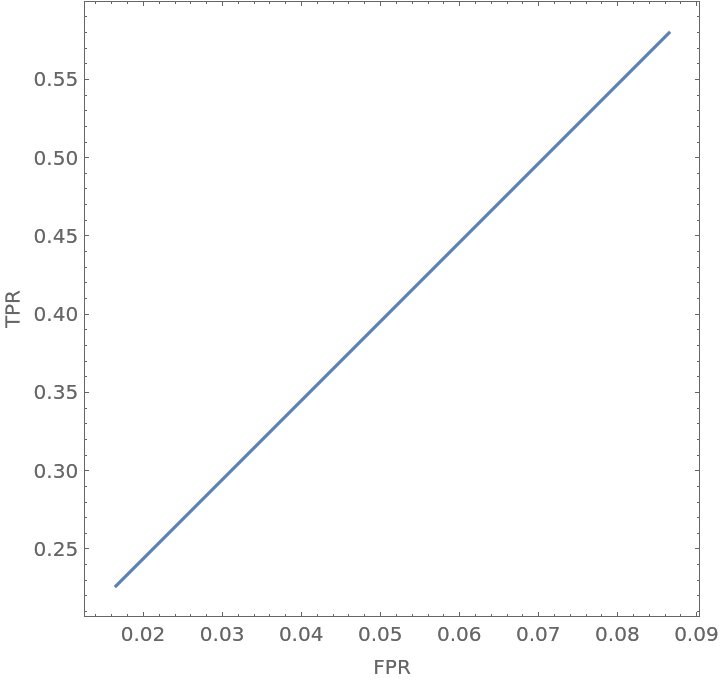

Show how the trajectory of false positive rates and true positive rates changes as one varies the second of two utility functions:

In[17]:=

$Manipulate[ With[{\[Gamma] = Query[Values, "survived"][ ResourceFunction["ExpectedClassifierMeasurements"][c, titanicTest, {w, 1 - w} -> { <| "died" -> <|"died" -> 0, "survived" -> -1|>, "survived" -> <|"died" -> -1, "survived" -> 0|> |>, <| "died" -> <|"died" -> 0, "survived" -> -fn|>, "survived" -> <|"died" -> -1, "survived" -> 0|> |> }, {"FalsePositiveRate", "TruePositiveRate"}]]}, ParametricPlot[\[Gamma], {w, 0, 1}, PlotRange -> {{0, 1}, {0, 1}}, AspectRatio -> 1, Frame -> True, FrameLabel -> {"FPR", "TPR"}] ], {{fn, 2}, 0.1, 4} ]$

Out[17]=

Publisher

Seth J. Chandler

Version History

1.0.0 – 14 October 2020

Related Resources

Author Notes

Given that the function works randomly, it is a little hard for me to come up with tough VerificationTests.

License Information

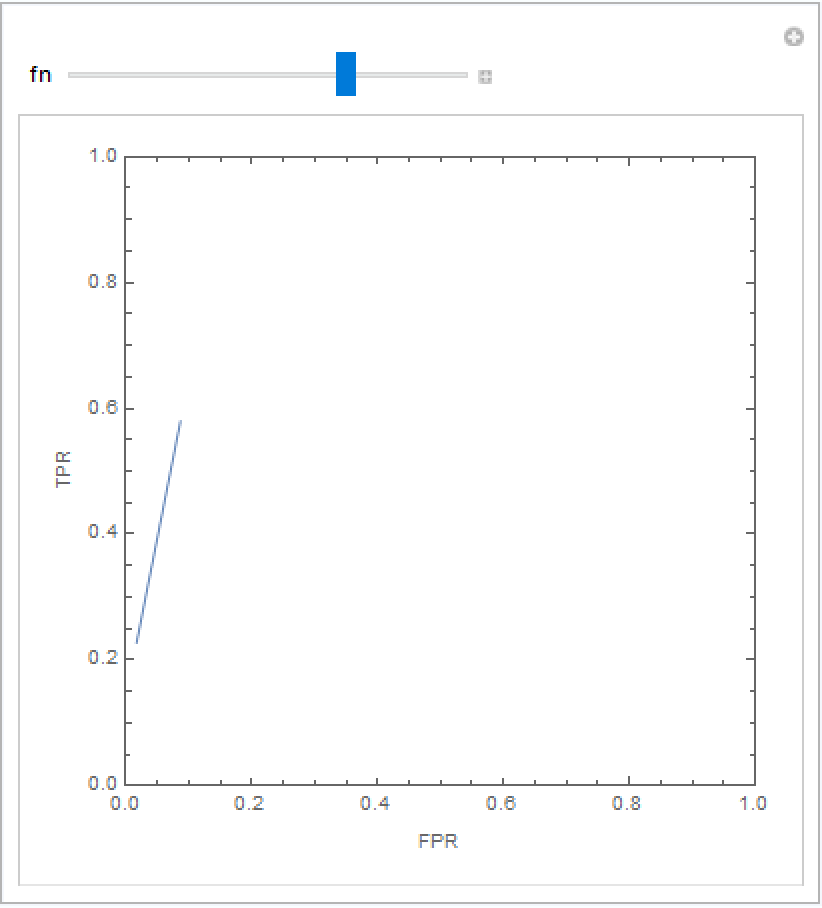This work is licensed under a Creative Commons Attribution 4.0 International License