Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a function that displays graphical objects at successive times
ResourceFunction["EvolutionViewFunction"][imgs] generates a function representing a time-evolving succession of graphical objects imgs. | |
ResourceFunction["EvolutionViewFunction"][imgs,mode] shows successive objects according to mode. | |
ResourceFunction["EvolutionViewFunction"][imgs,mode,times] shows objects at times specified by times. | |
ResourceFunction["EvolutionViewFunction"][imgs,mode,times,pos] places the origin of the sequence of objects at pos. |
| first stage | at first, an initial subsequence of objects is shown, whose form is determined by mode |
| mid-stages | a sequence of stages that implement the actual time evolution, each of which consists of six sub-stages |
| last stage | at last, the final subsequence of objects is shown, whose form is determined by mode |
| emerge | new elements appear in the subsequence currently shown |
| wait1 | after the emerge phase is finished, the elements are kept fixed |
| fadeaway | then some of the older elements fade away |
| wait2 | after the fadeaway phase is finished, the remaining elements are kept fixed |
| move | the remaining elements are moved aside to make space for new elements that are to emerge in the next sub-stage |
| wait3 | after the move phase is finished, the remaining elements are kept fixed |
| "Increase" | increase successively the number of elements shown until their number reaches the maximum default value; then update elements but keep their number constant (default) |
| "Decrease" | start with the sequence of the maximum number of elements and then decrease their number until a single element remains |
| "IncreaseDecrease" | at first increase the number of elements; then keep their number constant; at the end decrease their number to a single element |
| "Continue" | like "IncreaseDecrease" but the decreasing stage of the sequence is aligned to the opposite side |
| "Constant" | keep the number of elements shown constant |
| "OneByOne" | show only a single element at a time |
| {mode,maxnum} | specify mode as well as the maximum number maxnum of elements shown (set to 2 by default); when maxnum is set to 1, the mode is automatically switched to "OneByOne" |
| Automatic | each sub-stage lasts 1 unit of time (default) |
| dur | each sub-stage lasts dur units of time |
| {durem,durw1,durfade,durw2,durmove,durw3} | specify duration of each sub-stage |
| {{durem1,…},{durem2,…},…} | specify duration of each sub-stage for each mid-stage separately |
| {dursmid,{durfirst,durlast}} | specify durations dursmid for mid-stages using the above-mentioned formats and also separately set the duration of the first stage dursfirst and the last stage durlast |
| {dursmid,dursfirstlast,timestamps} | specify also absolute timestamps for the start of each mid-stage as well as the last stage |
| {Automatic,Automatic,timestamps} | specify only the timestamps |
| Alignment | Right | alignment of the sequence with respect to the pos |
| Direction | Left | direction of movement of elements |
| Dividers | Automatic | graphical object inserted between each two successive elements |
| ItemSize | 0.5 | size of each graphical object |
| RotateLabel | {True,π} | whether to rotate graphical objects depending on Direction |
| Spacings | 1 | spacing between the centers of each two successive elements |
| Verbose | False | whether to return the summary Association |
| "EmergeFunction" | Automatic | function applied to new elements |
| "FadeFunction" | Automatic | function applied to old elements |
| "NormalizeTimes" | False | whether to normalize the total duration of the sequence |
| Right | sequence aligned to the right (default) |
| Left | sequence aligned to the left |
| Center | sequence aligned to the center |
| Top | sequence aligned vertically to the top |
| Bottom | sequence aligned vertically to the bottom |
| None | no alignment applied |
| {hor,ver} | horizontal alignment hor, which can be set to Right,Left or Center, and vertical alignment ver, which can be set to Top,Bottom or Center |
| {hor,ver,rel} | specify also the relative alignment of elements within the sequence, possible values are Right,Left and Center |
| Left | move elements to the left (default) |
| Right | move elements to the right |
| Up | move elements upward |
| Down | move elements downward |
| ang | move elements along a line that subtends an angle ang with respect to the positive x-axis |
| {x,y} | move elements along a vector {x,y} |
| True | rotate both the elements and the dividers based on the setting of Direction |
| False | do not rotate anything |
| {rotelems,rotdivs} | whether to rotate elements and dividers is specified by rotelems and rotdivs, respectively |
| {rot,addang} | rotate both elements and dividers and add a constant angle offset of addang (default is {True,π}) |
| {{rot,addang}} | the same as above |
| {{rotelems,addangelems},{rotdivs,addangdivs}} | specify the rotation and the constant angle offset for elements and dividers separately |
| Automatic | new objects slowly emerge (default) |
| None | new objects appear immediately |
| fun | function fun is applied to each new object |
| {funfirst,funrest} | function funfirst is applied to the sequence of elements at the very beginning of the evolution and then function funrest is applied to each new object |
| Automatic | new objects slowly fade away (default) |
| None | new objects disappear immediately |
| fun | function fun is applied to each object that is to be disposed of |
| {funmost,funlast} | function funmost is applied to old elements in the course of the evolution and then function funlast is applied to the remaining sequence of objects |
Create a simple animation where one colored image follows another:
| In[1]:= | ![images = ResourceFunction["EvolutionViewFunction"][{\!\(\*
GraphicsBox[
TagBox[RasterBox[RawArray["Real32",{{{1., 0., 0.}}}], {{0, 1}, {1, 0}}, {0., 1.},
ColorFunction->RGBColor],
BoxForm`ImageTag["Real32", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{1, 1},
PlotRange->{{0, 1}, {0, 1}}]\), \!\(\*
GraphicsBox[
TagBox[RasterBox[RawArray["Real32",{{{0., 1., 0.}}}], {{0, 1}, {1, 0}}, {0., 1.},
ColorFunction->RGBColor],
BoxForm`ImageTag["Real32", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{1, 1},
PlotRange->{{0, 1}, {0, 1}}]\), \!\(\*
GraphicsBox[
TagBox[RasterBox[RawArray["Real32",{{{0., 0., 1.}}}], {{0, 1}, {1, 0}}, {0., 1.},
ColorFunction->RGBColor],
BoxForm`ImageTag["Real32", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{1, 1},
PlotRange->{{0, 1}, {0, 1}}]\), \!\(\*
GraphicsBox[
TagBox[RasterBox[RawArray["Real32",{{{0., 1., 1.}}}], {{0, 1}, {1, 0}}, {0., 1.},
ColorFunction->RGBColor],
BoxForm`ImageTag["Real32", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{1, 1},
PlotRange->{{0, 1}, {0, 1}}]\), \!\(\*
GraphicsBox[
TagBox[RasterBox[RawArray["Real32",{{{1., 0., 1.}}}], {{0, 1}, {1, 0}}, {0., 1.},
ColorFunction->RGBColor],
BoxForm`ImageTag["Real32", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{1, 1},
PlotRange->{{0, 1}, {0, 1}}]\), \!\(\*
GraphicsBox[
TagBox[RasterBox[RawArray["Real32",{{0.}}], {{0, 1}, {1, 0}}, {0., 1.},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Real32", ColorSpace -> "Grayscale", Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{1, 1},
PlotRange->{{0, 1}, {0, 1}}]\)}, "Constant"]
Animate[Graphics[images[t], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}}], {t, 0, 1}, AnimationRate -> 0.1]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/7e69dacb5db10c7f.png) |
| Out[2]= |  |
Represent a sequence of plots in time:
| In[3]:= | ![spirals = ParametricPlot[\[Theta] {Cos[\[Theta]], Sin[\[Theta]]}, {\[Theta], 0, #}, Axes -> False, PlotRange -> 5 \[Pi]] & /@ Range[\[Pi]/4, 5 \[Pi], \[Pi]/4];
spiralFun = ResourceFunction["EvolutionViewFunction"][
spirals, {"IncreaseDecrease", 4}, ItemSize -> 1, Spacings -> 1.3];
Animate[Graphics[spiralFun[t], PlotRange -> {{-4.5, 0.5}, 0.5 {-1, 1}}], {t, 0, 1}, AnimationRate -> 0.05]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/42296401728fcace.png) |
| Out[4]= |  |
Create a Tetris-like effect:
| In[5]:= | ![squares = Table[{Blue, Rectangle[-0.2 {1, 1}, 0.2 {1, 1}]}, 8];
tetris = ResourceFunction["EvolutionViewFunction"][
squares, {"IncreaseDecrease", 3}, Spacings -> 0.5, Direction -> Down, Alignment -> {Center, Bottom}, Dividers -> None];
Animate[Graphics[tetris[t], PlotRange -> {{-0.5, 0.5}, {-0.5, 1.5}}], {t, 0, 1}, AnimationRate -> 0.2]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/5d6759b547f218ef.png) |
| Out[78]= |  |
The graphical objects may be images:
| In[79]:= | ![imgs = ConstantImage[#, {1, 1}] & /@ {Red, Green, Blue, Cyan, Magenta,
Black};
images = ResourceFunction["EvolutionViewFunction"][imgs, Spacings -> 1.2];
Animate[Graphics[images[t], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}}], {t, 0, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/474f6ef4373aca61.png) |
| Out[81]= |  |
They may also be Graphics objects:
| In[82]:= | ![imgs = Graphics[{#, Disk[{0, 0}, 0.2]}] & /@ {Red, Green, Blue, Cyan, Magenta, Black};
graphics = ResourceFunction["EvolutionViewFunction"][imgs];
Animate[Graphics[graphics[t], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}}], {t, 0, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/2f6e62d4262bbfaa.png) |
| Out[83]= |  |
The head Graphics may be omitted:
| In[84]:= | ![imgs = {#, Disk[{0, 0}, 0.2]} & /@ {Red, Green, Blue, Cyan, Magenta, Black};
primitives = ResourceFunction["EvolutionViewFunction"][imgs];
Animate[Graphics[primitives[t], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}}], {t, 0, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/6a1e5666dffa64ff.png) |
| Out[86]= |  |
The default mode:
| In[87]:= |
| Out[88]= | 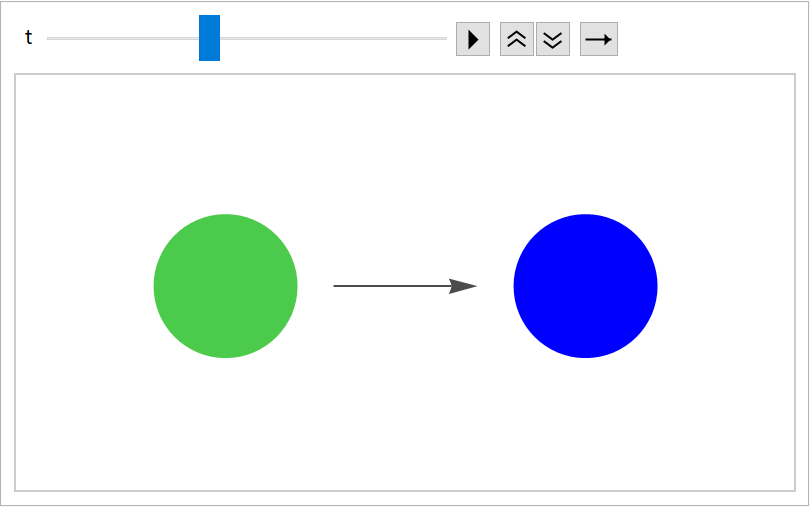 |
Use mode "Increase" with at most four images shown at a time:
| In[89]:= |
| Out[90]= | 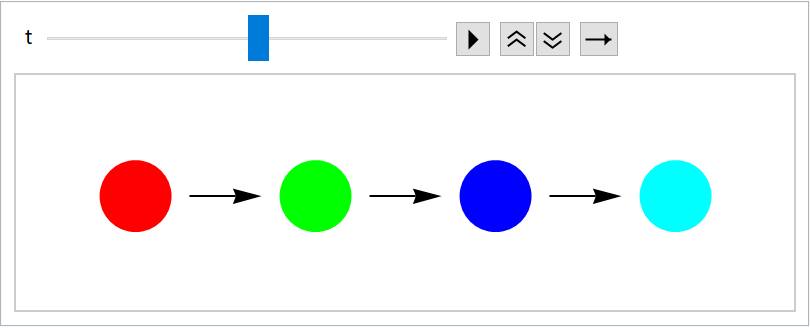 |
Do not restrict the maximum number of images shown:
| In[91]:= |
| Out[92]= | 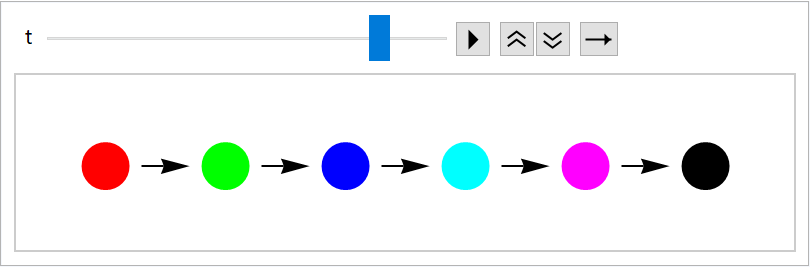 |
Use the default number:
| In[93]:= |
| Out[94]= | 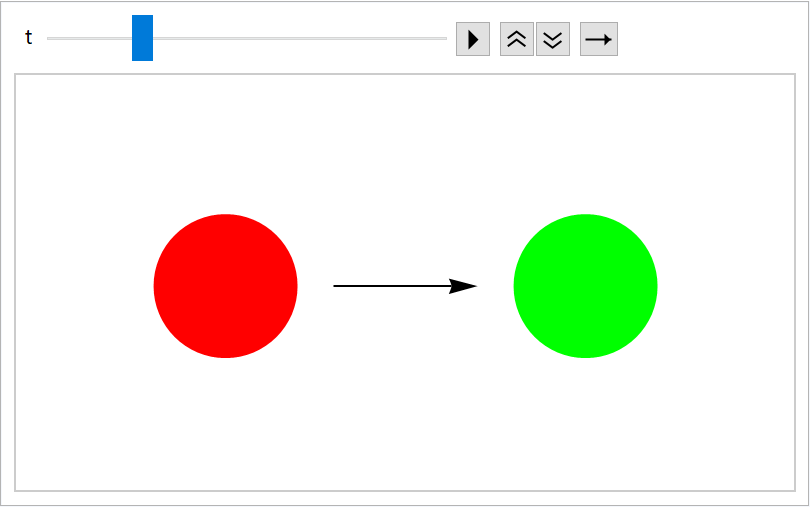 |
Mode "Increase" increases the number of shown images from one to a given maximum number:
| In[95]:= | ![increase = ResourceFunction["EvolutionViewFunction"][{{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}}, {"Increase", 3}];
Column[Framed@
Graphics[increase[#], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[NumberForm[#, {3, 3}]]] & /@ {0.2, 0.4, 0.55,
0.8, 0.95}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/4f758a594e620bb2.png) |
| Out[96]= | 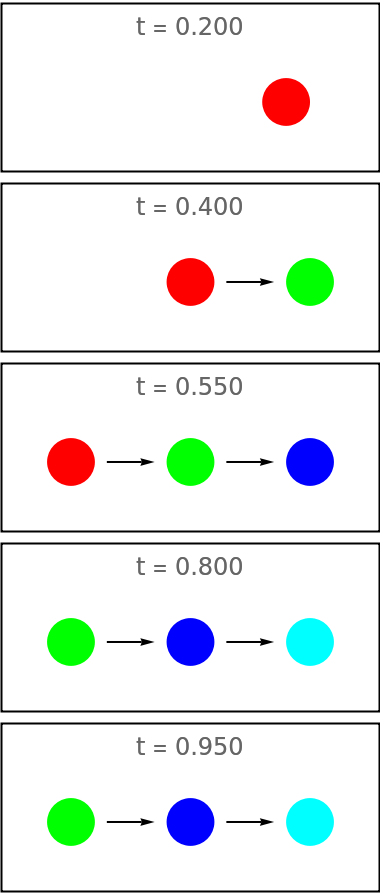 |
Mode "IncreaseDecrease" increases the number of shown images from one to a given maximum number and then decreases it again to one:
| In[97]:= | ![increaseDecrease = ResourceFunction["EvolutionViewFunction"][{{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}}, {"IncreaseDecrease", 3}];
Column[Framed@
Graphics[increaseDecrease[#], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[NumberForm[#, {3, 3}]]] & /@ {0.2, 0.4, 0.55,
0.8, 0.95}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/00cf3af8c3f2a37a.png) |
| Out[98]= | 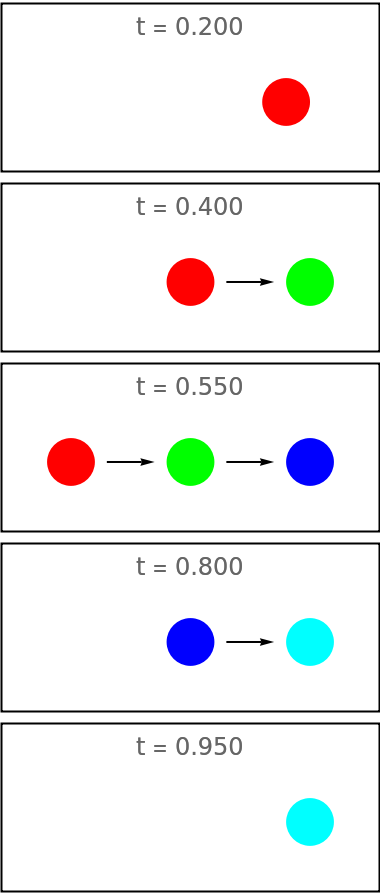 |
When the maximum specified number is too large, it is automatically adjusted:
| In[99]:= | ![increaseDecreaseLim = ResourceFunction["EvolutionViewFunction"][{{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}}, {"IncreaseDecrease", 10}];
Column[Framed@
Graphics[increaseDecreaseLim[#], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[NumberForm[#, {3, 3}]]] & /@ {0.2, 0.4, 0.55,
0.8, 0.95}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/511319c275d4fb31.png) |
| Out[100]= | 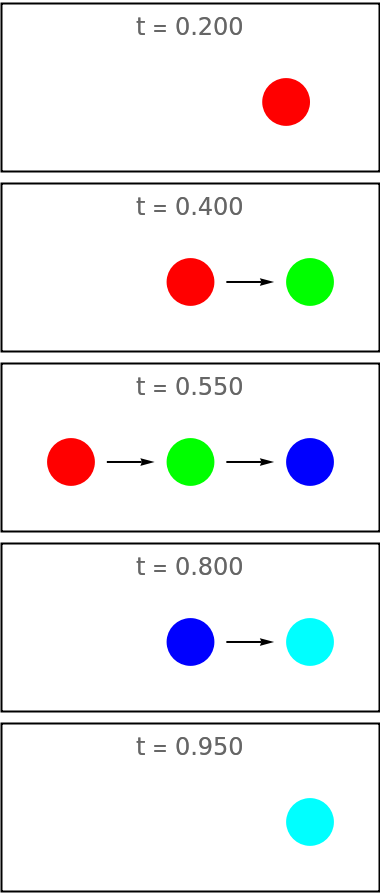 |
Mode "Continue" works similar to "IncreaseDecrease" but the images in the decreasing part are aligned to the opposite side:
| In[101]:= | ![continue = ResourceFunction["EvolutionViewFunction"][{{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}}, {"Continue", 3}];
Column[Framed@
Graphics[continue[#], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[NumberForm[#, {3, 3}]]] & /@ {0.2, 0.215, 0.55, 0.8, 0.95}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/643e2592436aa472.png) |
| Out[102]= |  |
Mode "Decrease" works similar to "Increase" but the number of images decreases:
| In[103]:= | ![decrease = ResourceFunction["EvolutionViewFunction"][{{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}}, {"Decrease", 3}];
Column[Framed@
Graphics[decrease[#], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[NumberForm[#, {3, 3}]]] & /@ {0.2, 0.4, 0.55,
0.8, 0.95}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/23ef36c666ffb32f.png) |
| Out[104]= | 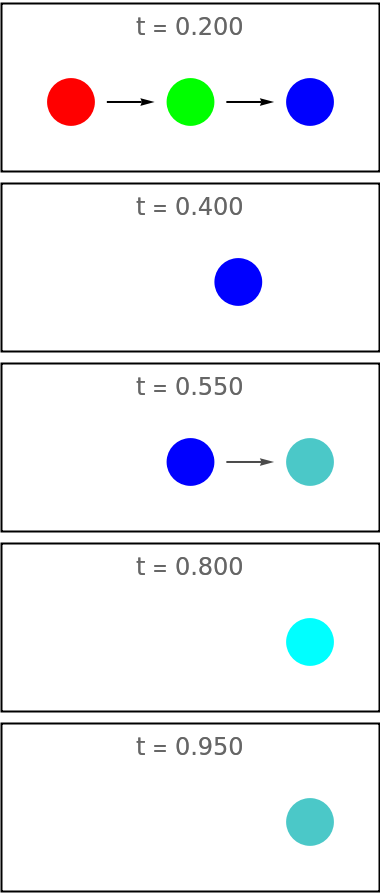 |
Mode "Constant" keeps the number of images constant:
| In[105]:= | ![constant = ResourceFunction["EvolutionViewFunction"][{{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}}, {"Constant", 3}];
Column[Framed@
Graphics[constant[#], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[NumberForm[#, {3, 3}]]] & /@ {0.2, 0.4, 0.55,
0.8, 0.95}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/6cc086299adfa3f9.png) |
| Out[106]= | 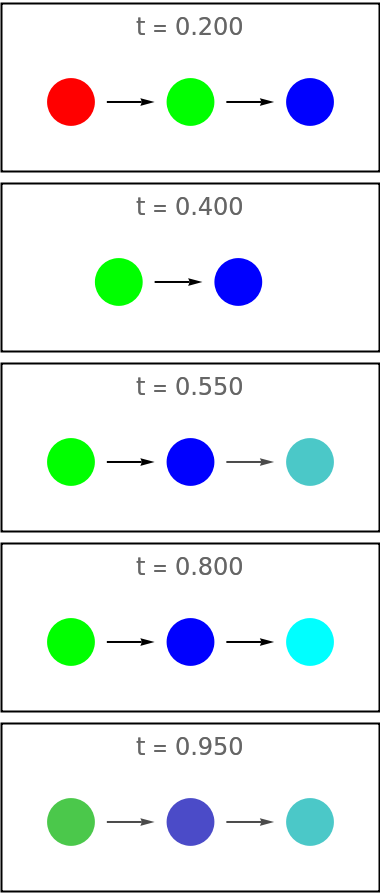 |
Mode "OneByOne" shows always only a single image at a time:
| In[107]:= | ![oneByOne = ResourceFunction["EvolutionViewFunction"][{{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}}, "OneByOne"];
Column[Framed@
Graphics[oneByOne[#], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[NumberForm[#, {3, 3}]]] & /@ {0.1, 0.15, 0.55, 0.8, 0.95}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/1ea7e902a4ad1e97.png) |
| Out[108]= |  |
This mode is used automatically whenever the maximum specified number is set to 1 for any of the other modes:
| In[109]:= | ![continueOne = ResourceFunction["EvolutionViewFunction"][{{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}}, {"Continue", 1}];
Column[Framed@
Graphics[continueOne[#], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[NumberForm[#, {3, 3}]]] & /@ {0.1, 0.15, 0.55, 0.8, 0.95}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/226a8380c4856070.png) |
| Out[110]= |  |
Specify the time duration of each step of the animation:
| In[111]:= | ![time = 0.2;
imgs = {
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{1., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{0.}},"Real32"], "Real32", ColorSpace -> "Grayscale", Interleaving -> None]};
givenDurs = ResourceFunction["EvolutionViewFunction"][imgs, "Constant", time];
Framed@Graphics[givenDurs[#], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}},
PlotLabel -> "t = " <> ToString[N@#]] & /@ Subdivide[0, 1, 5]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/70c953710dce4768.png) |
| Out[112]= | 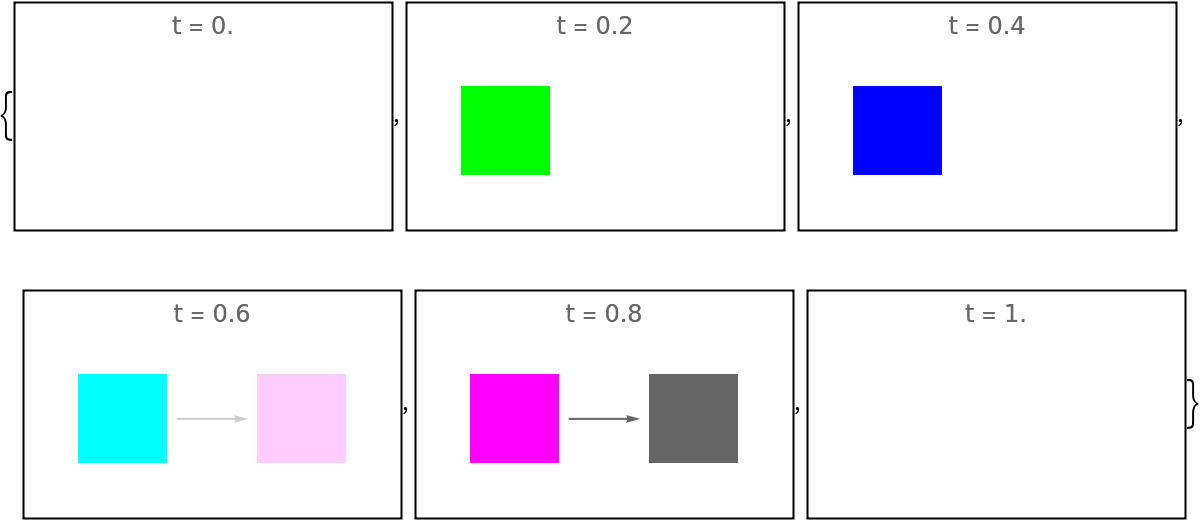 |
By default, the total time duration is set to 1; turn the normalization off:
| In[113]:= | ![givenDursNonNorm = ResourceFunction["EvolutionViewFunction"][imgs, "Constant", time, "NormalizeTimes" -> False];
Framed@Graphics[givenDursNonNorm[#], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[N@#]] & /@ Subdivide[0, 6.4, 5]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/66ea5ad1591d3a0c.png) |
| Out[114]= | 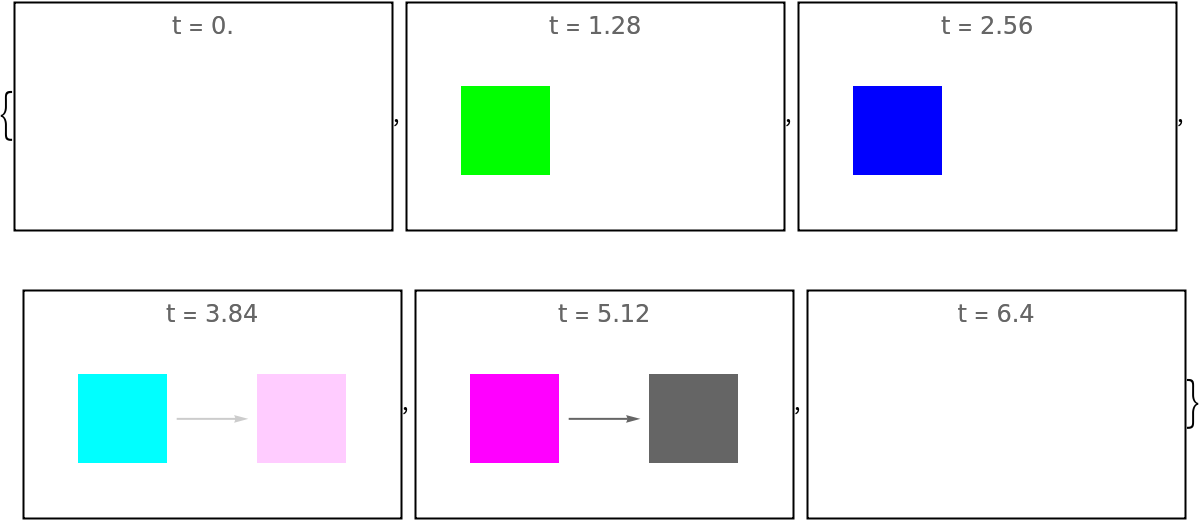 |
Total duration can be read out by setting Verbose to True:
| In[115]:= |
| Out[115]= |
Set different durations for each sub-stage:
| In[116]:= | ![times = {5, 1, 5, 1, 5, 1};
imgs = {
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{1., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{0.}},"Real32"], "Real32", ColorSpace -> "Grayscale", Interleaving -> None]};
givenSubDurs = ResourceFunction["EvolutionViewFunction"][imgs, "Constant", times];](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/2e3d5e6673e03d0d.png) |
Get corresponding timestamps:
| In[117]:= | ![timesummary = ResourceFunction["EvolutionViewFunction"][imgs, "Constant", times, Verbose -> True]["Times"];
{time1, time2} = timesummary["Timestamps for mid stages"][[{2, 3}]];
durmid = First@
ReleaseHold@timesummary["Individual durations for mid substages"];
midstage = time1 + Normalize[Accumulate[Prepend[durmid, 0]], Max] (time2 - time1) // N](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/77c0c6b43cc7487e.png) |
| Out[118]= |
Show the evolution and timestamps:
| In[119]:= | ![MapThread[
Framed@Graphics[givenSubDurs[#], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[#] <> " \[LongDash] " <> ToString[#2]] &, {midstage, {"Start", "Emerging finished", "Waiting 1 finished", "Fading away finished", "Waiting 2 finished",
"Movement finished", "Waiting 3 finished"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/3f2c5d56363c75d0.png) |
| Out[119]= | 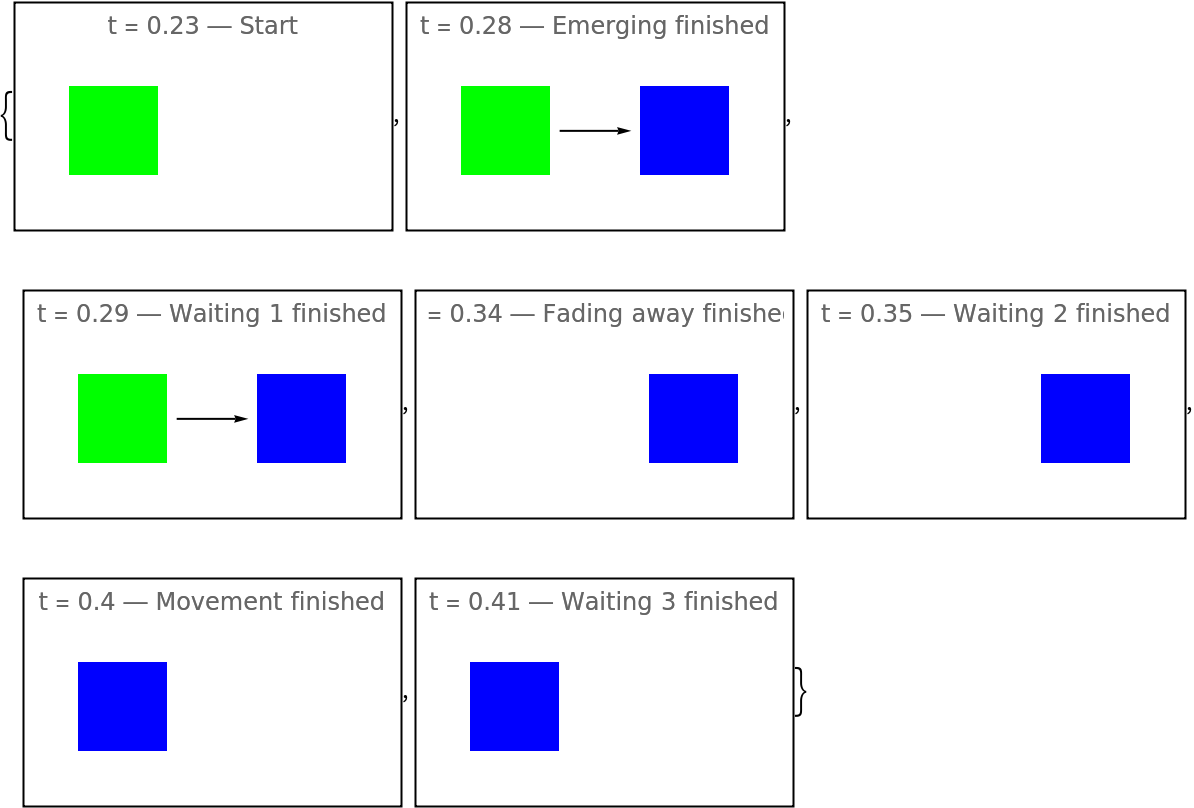 |
Durations can be specified for each mid-stage independently:
| In[120]:= | ![times = {{5, 1, 5, 1, 5, 1}, {5, 1, 1, 1, 1, 1}, {5, 5, 4, 3, 2, 1}, {5, 1, 1, 1, 1, 1}, {5, 2, 5, 1, 5, 3}};
imgs = {
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{1., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{0.}},"Real32"], "Real32", ColorSpace -> "Grayscale", Interleaving -> None]};
eachStage = ResourceFunction["EvolutionViewFunction"][imgs, "Constant", times];](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/65c64b251ab0c768.png) |
The number of mid-stages is given in "Number of mid stages" field of the summary Association:
| In[121]:= |
| Out[121]= |
This number is calculated automatically and can be read out also when no explicit time specification is given:
| In[122]:= |
| Out[122]= |
Durations of the very first and very last stage of the animation can be set separately from the rest:
| In[123]:= | ![durfirst = 0.2;
durlast = 0.6;
imgs = {
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{1., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{0.}},"Real32"], "Real32", ColorSpace -> "Grayscale", Interleaving -> None]};
Dataset[ResourceFunction["EvolutionViewFunction"][imgs, "Constant", {Automatic, {durfirst, durlast}}, "NormalizeTimes" -> False, Verbose -> True]]["Times"]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/0758f28977da8fc2.png) |
| Out[124]= |  |
By default, the total duration is normalized to one and so the final durations might be different from the input values:
| In[125]:= | ![Dataset[ResourceFunction["EvolutionViewFunction"][imgs, "Constant", {Automatic, {durfirst, durlast}}, "NormalizeTimes" -> True, Verbose -> True]]["Times"]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/66e077140b287fd1.png) |
| Out[125]= | 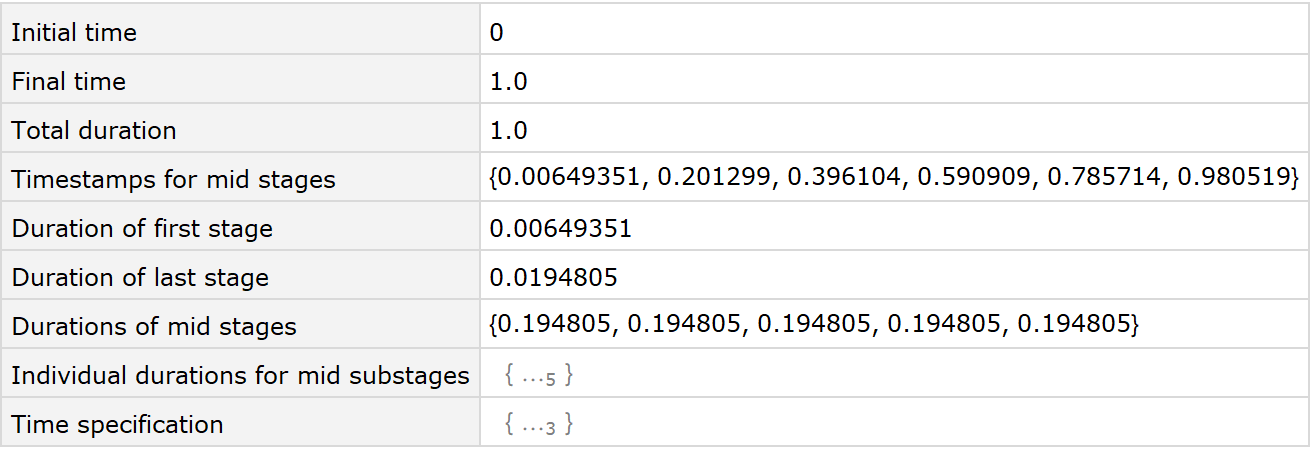 |
Set explicit timestamps that specify the beginning of each mid-stage:
| In[126]:= | ![durfirst = 0.2;
durlast = 0.6;
timestamps = {1, 2, 3, 6, 7, 8};
evolTimestamps = ResourceFunction[
"EvolutionViewFunction"][{
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{1., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{0.}},"Real32"], "Real32", ColorSpace -> "Grayscale", Interleaving -> None]}, "Constant", {Automatic, {durfirst, durlast}, timestamps}, "EmergeFunction" -> None];
Framed@Graphics[evolTimestamps[#], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[N@#]] & /@ timestamps](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/3d58e674bb2827e7.png) |
| Out[127]= | 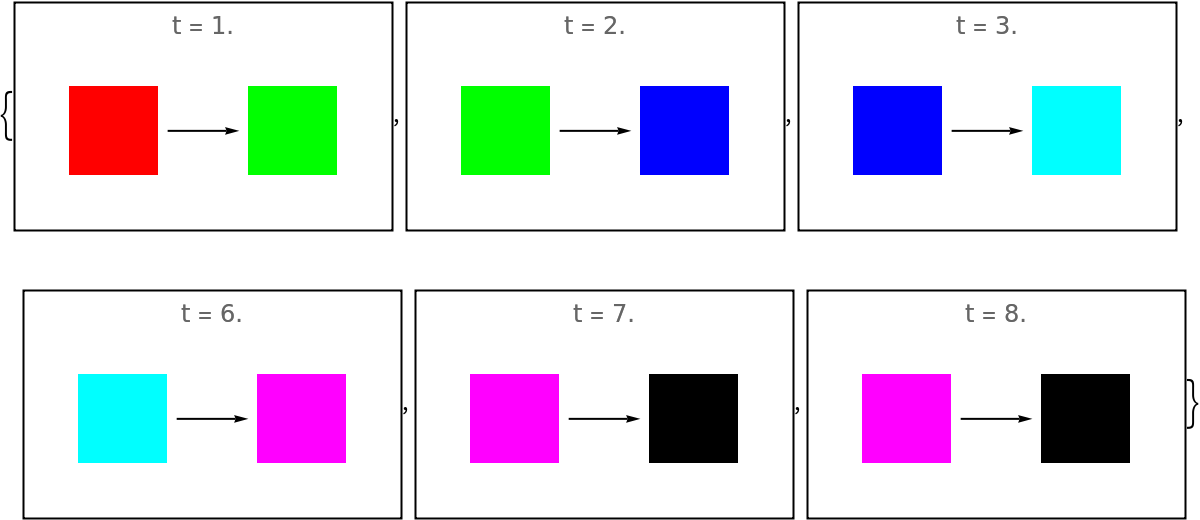 |
The beginning of the animation is determined from the duration of the first stage:
| In[128]:= | ![starttime = First[timestamps] - durfirst;
Framed@Graphics[evolTimestamps[#], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[N@#]] &@starttime](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/569928836d78c980.png) |
| Out[129]= |  |
The end of the animation is determined from the duration of the last stage:
| In[130]:= | ![stoptime = Last[timestamps] + durlast;
Framed@Graphics[evolTimestamps[#], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[N@#]] &@stoptime](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/02bae9a946ad9b55.png) |
| Out[131]= |  |
When absolute timestamps are used, the durations of individual sub-stages are rescaled to fit:
| In[132]:= | ![durmid = {5, 1, 5, 1, 5, 1};
durfirst = 0.2;
durlast = 0.6;
timestamps = {1, 2, 3, 6};
midstage = timestamps[[2]] + Normalize[Accumulate[Prepend[durmid, 0]], Max] (timestamps[[3]] - timestamps[[2]]) // N](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/4fabd91d81243349.png) |
| Out[133]= |
| In[134]:= | ![evolRescaled = ResourceFunction[
"EvolutionViewFunction"][{
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True]}, "Constant", {durmid, {durfirst, durlast}, timestamps}];
MapThread[
Framed@Graphics[evolRescaled[#], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[NumberForm[N@#, 3]] <> " \[LongDash] " <> ToString[#2]] &, {midstage, {"Start", "Emerging finished", "Waiting 1 finished", "Fading away finished", "Waiting 2 finished",
"Movement finished", "Waiting 3 finished"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/4e5ba80fc9423636.png) |
| Out[135]= | 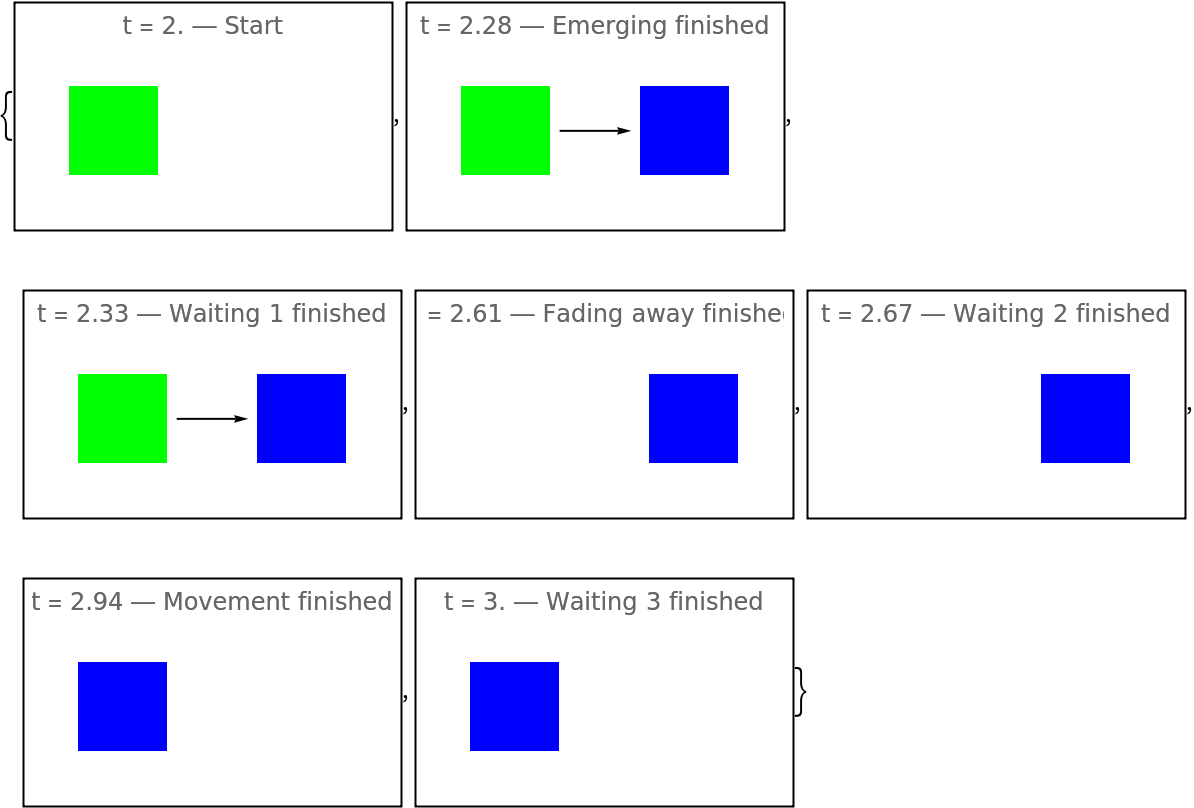 |
Compare with the animation itself:
| In[136]:= |
| Out[136]= | 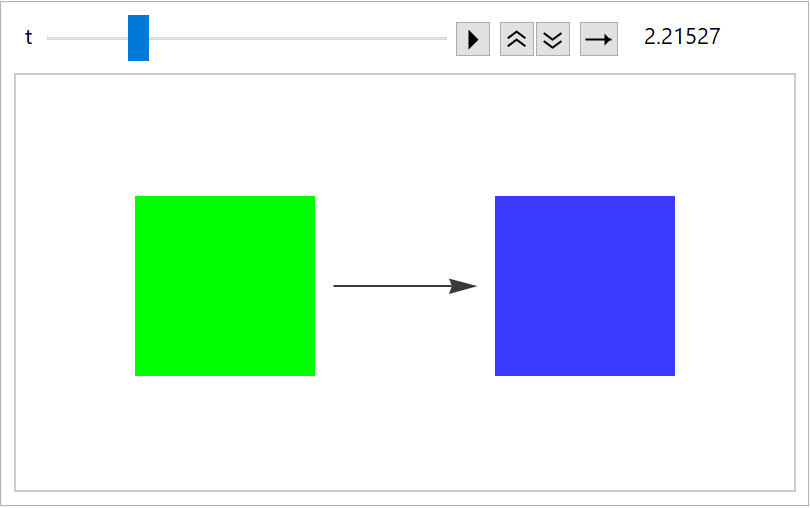 |
Place the origin of the emerging images at a given point:
| In[137]:= | ![custompos = {0.3, 0.55};
imgs = {
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{1., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{0.}},"Real32"], "Real32", ColorSpace -> "Grayscale", Interleaving -> None]};
evolfunDefault = ResourceFunction["EvolutionViewFunction"][imgs, "Constant", Automatic];
evolfunCustom = ResourceFunction["EvolutionViewFunction"][imgs, "Constant", Automatic, custompos];
Graphics[{evolfunDefault[0.1], evolfunCustom[0.1], Text[Style[{0, 0}, 20], {0, 0}, {0, 1}], Text[Style[custompos, 20], custompos, {0, 1}], PointSize[0.02], Point[{{0, 0}, custompos}]}, PlotRange -> {{-1.5, 0.8}, {-0.5, 1.2}}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/159f7a687cbaabe8.png) |
| Out[138]= | 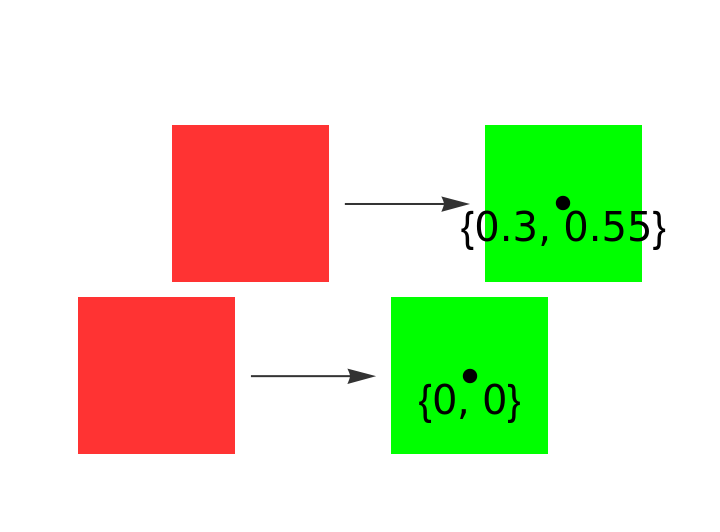 |
Turn off the slow-emerge effect for new images:
| In[139]:= | ![noEmerge = ResourceFunction["EvolutionViewFunction"][{{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}}, {"Constant", 3}, "EmergeFunction" -> None];
Animate[Graphics[noEmerge[t], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}], {t, 0, 1}, AnimationRate -> .1]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/2fbc2bb1e18de6e4.png) |
| Out[140]= | 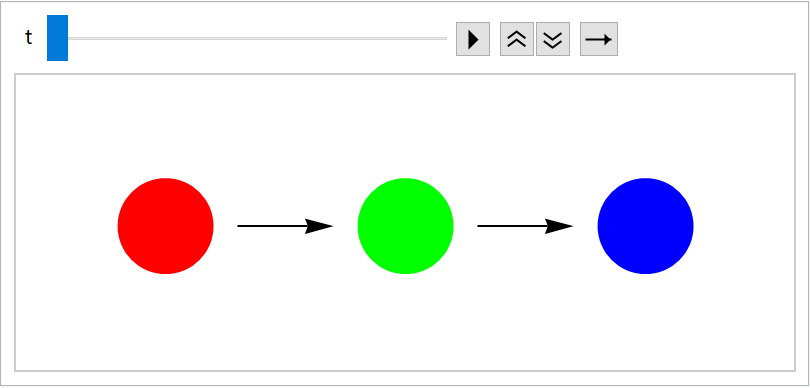 |
Specify a custom function:
| In[141]:= | ![emfun[gr_, t_?NumericQ] := Scale[gr, t]
scaleUp = ResourceFunction["EvolutionViewFunction"][{{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}}, {"Constant", 3}, "EmergeFunction" -> emfun];
Animate[Graphics[scaleUp[t], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}], {t, 0, 1}, AnimationRate -> .1]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/1a8461ad762ba8f1.png) |
| Out[142]= | 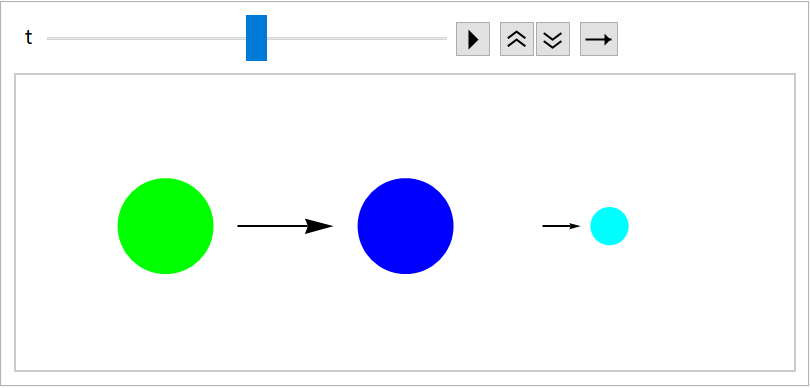 |
Specify different "EmergeFunction" for the very first stage and the rest:
| In[143]:= | ![emfunFirst[gr_, t_?NumericQ] := Scale[gr, t]
emfunRest[gr_, t_?NumericQ] := gr /. col_?ColorQ :> Blend[{Transparent, col}, t]
scaleUpEm = ResourceFunction["EvolutionViewFunction"][{{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}}, {"Constant", 3}, "EmergeFunction" -> {emfunFirst, emfunRest}];
Animate[Graphics[scaleUpEm[t], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}], {t, 0, 1}, AnimationRate -> .1]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/2ced75c5b4c2f779.png) |
| Out[144]= | 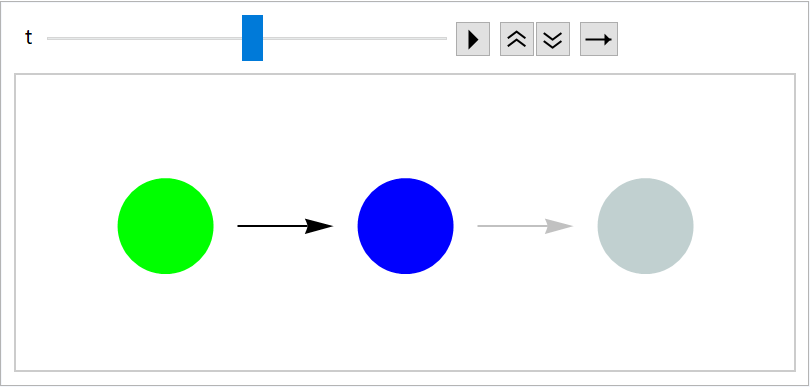 |
Turn off the slow-fade-away effect for old images:
| In[145]:= | ![noFadeAway = ResourceFunction["EvolutionViewFunction"][{{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}}, {"Constant", 3}, "FadeFunction" -> None];
Animate[Graphics[noFadeAway[t], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}], {t, 0, 1}, AnimationRate -> .1]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/7d762ac1cf39b866.png) |
| Out[146]= | 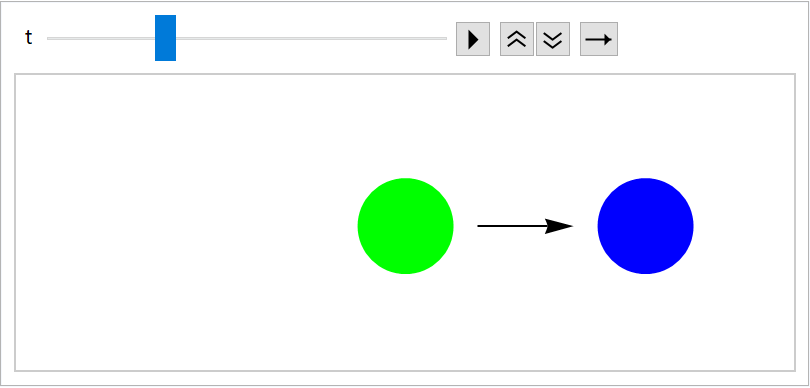 |
Specify a custom function:
| In[147]:= | ![fadefun[gr_, t_?NumericQ] := Scale[gr, t]
scaleDown = ResourceFunction["EvolutionViewFunction"][{{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}}, {"Constant", 3}, "FadeFunction" -> fadefun];
Animate[Graphics[scaleDown[t], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}], {t, 0, 1}, AnimationRate -> .1]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/79cfb2f302f03659.png) |
| Out[148]= | 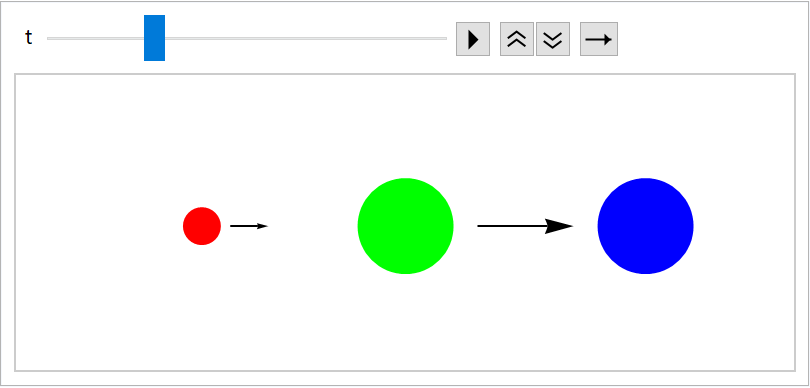 |
Specify different "FadeFunction" for the very last stage and the rest:
| In[149]:= | ![fadefunMost[gr_, t_?NumericQ] := Scale[gr, t]
fadefunLast[gr_, t_?NumericQ] := gr /. col_?ColorQ :> Blend[{Black, col}, t]
scaleDownFade = ResourceFunction["EvolutionViewFunction"][{{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}}, {"Constant", 3}, "FadeFunction" -> {fadefunMost, fadefunLast}];
Animate[Graphics[scaleDownFade[t], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}], {t, 0, 1}, AnimationRate -> .1]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/0c39ec01994c1a17.png) |
| Out[150]= | 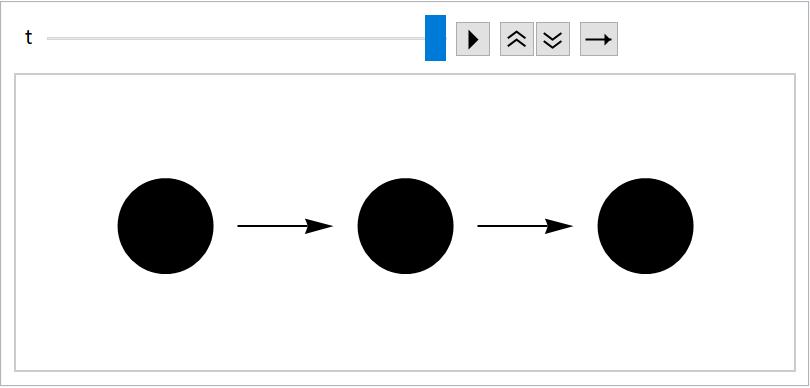 |
By default, the time intervals are normalized such that the total duration of animation is 1:
| In[151]:= | ![timeint = 0.2;
imgs = {{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}};
normTimes = ResourceFunction["EvolutionViewFunction"][imgs, {"Constant", 3}, timeint];
Framed@Graphics[normTimes[#], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}},
PlotLabel -> "t = " <> ToString[N@#]] & /@ Subdivide[5]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/7de491f4dfe3bd68.png) |
| Out[152]= | 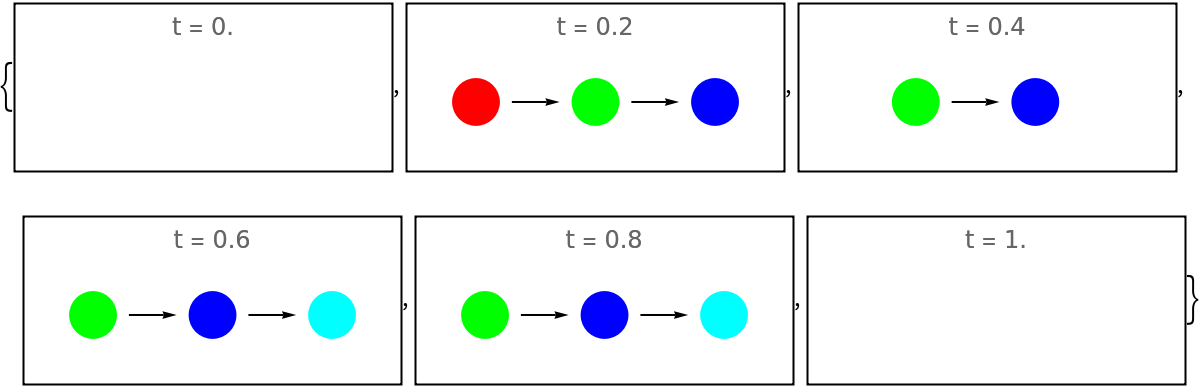 |
Set "NormalizeTimes" to False to turn off the normalization:
| In[153]:= | ![notNormTimes = ResourceFunction["EvolutionViewFunction"][imgs, {"Constant", 3}, timeint, "NormalizeTimes" -> False];
Framed@Graphics[notNormTimes[#], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[N@#]] & /@ Subdivide[0, 2.8, 5]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/5cec7b38fdd42454.png) |
| Out[154]= | 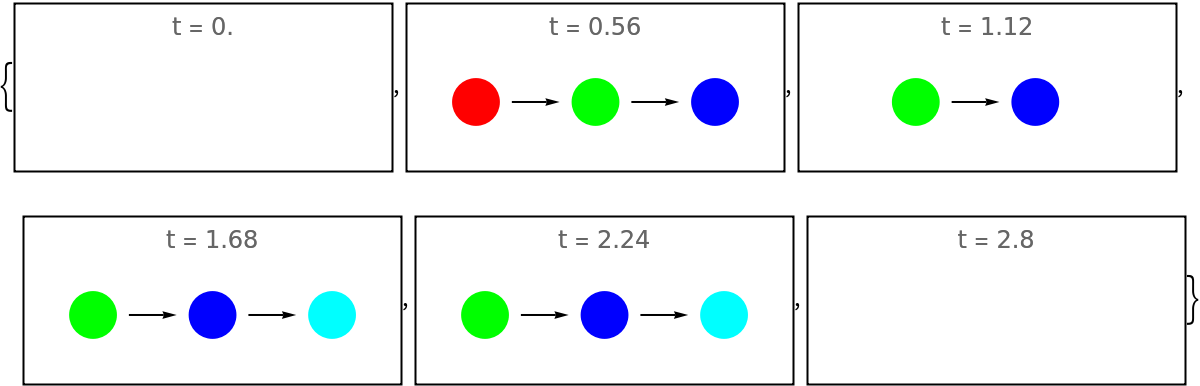 |
The total duration of the animation can be obtained by setting Verbose to True:
| In[155]:= |
| Out[155]= |
When explicit timestamps are used, the value of "NormalizeTimes" is ignored:
| In[156]:= | ![explicitTimestamps = ResourceFunction["EvolutionViewFunction"][{{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}}, {"Constant", 3}, {Automatic, Automatic, {1, 2, 3}}, "NormalizeTimes" -> True];
Framed@Graphics[explicitTimestamps[#], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[N@#]] & /@ Subdivide[0, 4, 5]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/01eec2afd7d517a5.png) |
| Out[157]= | 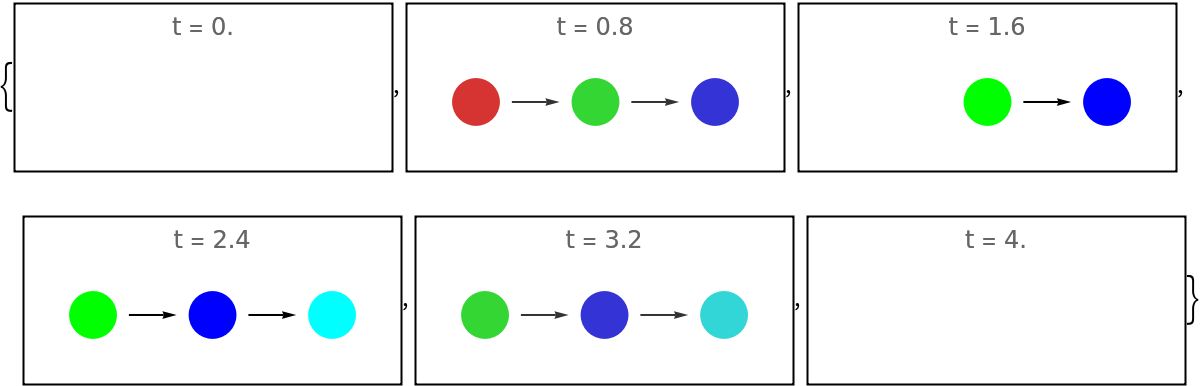 |
The total duration:
| In[158]:= |
| Out[158]= |
Summary of different internal parameters can be displayed by setting Verbose to True:
| In[159]:= | ![imgs = {\!\(\*
GraphicsBox[
TagBox[RasterBox[RawArray["Real32",{{{1., 0., 0.}}}], {{0, 1}, {1, 0}}, {0., 1.},
ColorFunction->RGBColor],
BoxForm`ImageTag["Real32", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{1, 1},
PlotRange->{{0, 1}, {0, 1}}]\), \!\(\*
GraphicsBox[
TagBox[RasterBox[RawArray["Real32",{{{0., 1., 0.}}}], {{0, 1}, {1, 0}}, {0., 1.},
ColorFunction->RGBColor],
BoxForm`ImageTag["Real32", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{1, 1},
PlotRange->{{0, 1}, {0, 1}}]\), \!\(\*
GraphicsBox[
TagBox[RasterBox[RawArray["Real32",{{{0., 0., 1.}}}], {{0, 1}, {1, 0}}, {0., 1.},
ColorFunction->RGBColor],
BoxForm`ImageTag["Real32", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{1, 1},
PlotRange->{{0, 1}, {0, 1}}]\)};
summary = ResourceFunction["EvolutionViewFunction"][imgs, Verbose -> True];
Dataset[summary]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/6e4f112dda335b2f.png) |
| Out[160]= | 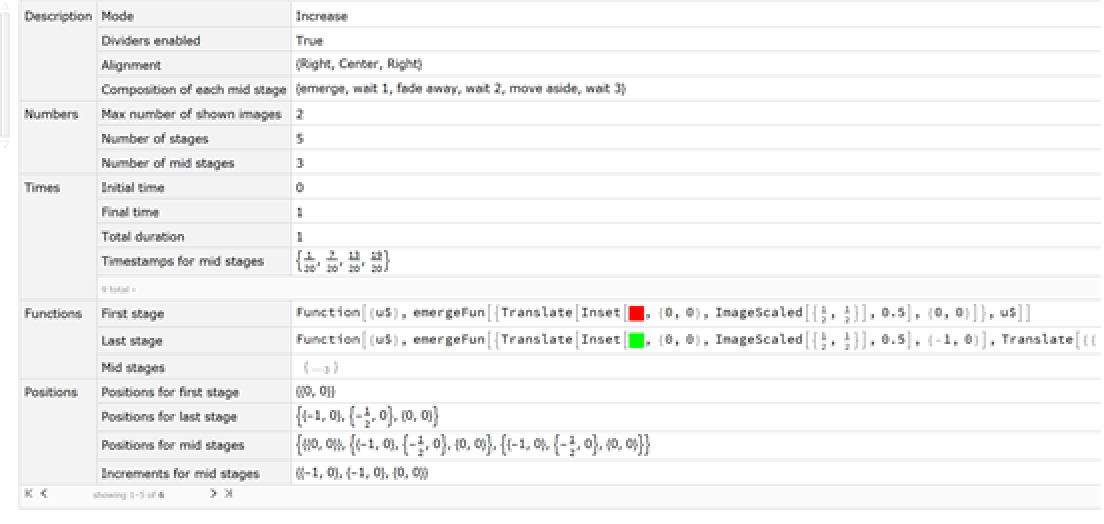 |
For precise synchronization with other animated elements, "Timestamps for mid stages" and "Time specification" are especially relevant:
| In[161]:= |
| Out[161]= |
| In[162]:= |
| Out[162]= |
| In[163]:= |
| Out[163]= |
The latter can be plugged back into EvolutionViewFunction as the time specification and then manually modified:
| In[164]:= | ![evolfunOld = ResourceFunction["EvolutionViewFunction"][imgs, Automatic, summary["Times", "Time specification"], Spacings -> 1.2];
newtimes = summary["Times", "Time specification"];
newtimes[[2, 2]] = 3;
evolfunNew = ResourceFunction["EvolutionViewFunction"][imgs, Automatic, newtimes,
Spacings -> 1.2];](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/02879d626eb5dd59.png) |
The new function has the last fade-away stage a little longer:
| In[165]:= | ![{Framed@Graphics[evolfunOld[0.99], PlotLabel -> Column[{Style["evolfun", Bold], "t = 0.99"}, Alignment -> Center]], Framed@Graphics[evolfunNew[0.99], PlotLabel -> Column[{Style["evolfunNew", Bold], "t = 0.99"}, Alignment -> Center]]}](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/29be3dc905feaae8.png) |
| Out[165]= |  |
Turn off the default dividers:
| In[166]:= | ![noDividers = ResourceFunction["EvolutionViewFunction"][{{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}}, {"Constant", 3}, Dividers -> None];
Animate[Graphics[noDividers[t], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}], {t, 0, 1}, AnimationRate -> .1]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/03eb24aabec73c41.png) |
| Out[167]= | 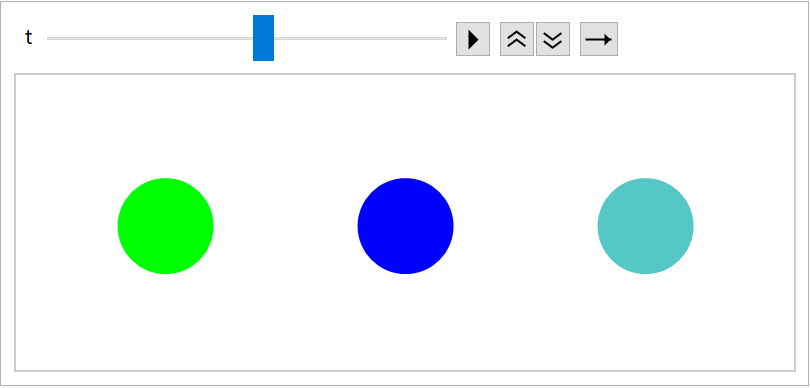 |
Use custom dividers:
| In[168]:= | ![div = Graphics[{Gray, Polygon[{{0, -0.5}, {1, 0}, {0, 0.5}}]}];
triangles = ResourceFunction["EvolutionViewFunction"][{{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 1],
Disk[{0, 0}, 0.2]}, {
RGBColor[1, 0, 1],
Disk[{0, 0}, 0.2]}}, {"Constant", 3}, Dividers -> div];
Animate[Graphics[triangles[t], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}], {t, 0, 1}, AnimationRate -> .1]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/19a930ef2a5df005.png) |
| Out[169]= | 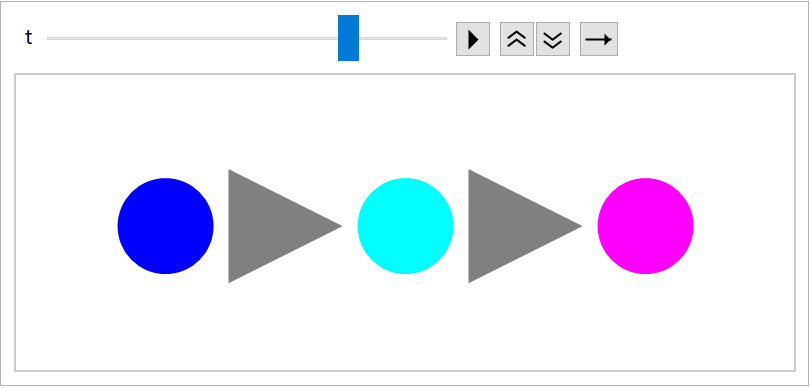 |
By default, images as well as dividers are rotated according to the direction of movement:
| In[170]:= | ![imgs = {
Graphics[{
RGBColor[0, 1, 0],
Rectangle[{-0.2, -0.2}, {0.2, 0.2}],
Text[
Style[1, 50, Bold,
GrayLevel[0]], {0, 0}]}],
Graphics[{
RGBColor[0, 1, 0],
Rectangle[{-0.2, -0.2}, {0.2, 0.2}],
Text[
Style[2, 50, Bold,
GrayLevel[0]], {0, 0}]}],
Graphics[{
RGBColor[0, 1, 0],
Rectangle[{-0.2, -0.2}, {0.2, 0.2}],
Text[
Style[3, 50, Bold,
GrayLevel[0]], {0, 0}]}],
Graphics[{
RGBColor[0, 1, 0],
Rectangle[{-0.2, -0.2}, {0.2, 0.2}],
Text[
Style[4, 50, Bold,
GrayLevel[0]], {0, 0}]}],
Graphics[{
RGBColor[0, 1, 0],
Rectangle[{-0.2, -0.2}, {0.2, 0.2}],
Text[
Style[5, 50, Bold,
GrayLevel[0]], {0, 0}]}],
Graphics[{
RGBColor[0, 1, 0],
Rectangle[{-0.2, -0.2}, {0.2, 0.2}],
Text[
Style[6, 50, Bold,
GrayLevel[0]], {0, 0}]}],
Graphics[{
RGBColor[0, 1, 0],
Rectangle[{-0.2, -0.2}, {0.2, 0.2}],
Text[
Style[7, 50, Bold,
GrayLevel[0]], {0, 0}]}],
Graphics[{
RGBColor[0, 1, 0],
Rectangle[{-0.2, -0.2}, {0.2, 0.2}],
Text[
Style[8, 50, Bold,
GrayLevel[0]], {0, 0}]}]};
evolfunRot = ResourceFunction["EvolutionViewFunction"][imgs, "Constant", Direction -> 80 Degree];
evolfunNoRot = ResourceFunction["EvolutionViewFunction"][imgs, "Constant", Direction -> 80 Degree, RotateLabel -> False];
{
Framed@Graphics[evolfunRot[0.2], PlotRange -> {{-0.5, 0.5}, {-1., 1.}}, PlotLabel -> "RotateLabel\[Rule]True"],
Framed@Graphics[evolfunNoRot[0.2], PlotRange -> {{-0.5, 0.5}, {-1., 1.}}, PlotLabel -> "RotateLabel\[Rule]False"]
}](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/152b91cc2efbb79e.png) |
| Out[171]= |  |
Set the spacings between the centers of graphical objects:
| In[172]:= | ![imgs = {
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{1., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{0.}},"Real32"], "Real32", ColorSpace -> "Grayscale", Interleaving -> None]};
evolfunNarrow = ResourceFunction["EvolutionViewFunction"][imgs, "Constant", Spacings -> 1];
evolfunWide = ResourceFunction["EvolutionViewFunction"][imgs, "Constant", Spacings -> 2];
{
Framed@Graphics[evolfunNarrow[0.0975], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "Spacings\[Rule]1"],
Framed@Graphics[evolfunWide[0.0975], PlotRange -> {{-2.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "Spacings\[Rule]2"]
}](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/523c1f01b67196df.png) |
| Out[173]= |  |
The Spacings value always refers to the spacing in the direction specified by Direction:
| In[174]:= | ![imgs = {
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{1., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{0.}},"Real32"], "Real32", ColorSpace -> "Grayscale", Interleaving -> None]};
evolfunNarrow = ResourceFunction["EvolutionViewFunction"][imgs, "Constant", Spacings -> 1, Direction -> 80 Degree, Alignment -> {Left, Bottom}];
evolfunWide = ResourceFunction["EvolutionViewFunction"][imgs, "Constant", Spacings -> 2, Direction -> 80 Degree, Alignment -> {Left, Bottom}];
{
Framed@Graphics[evolfunNarrow[0.0975], PlotRange -> {{-0.5, 1}, {-0.5, 2.5}}, PlotLabel -> "Spacings\[Rule]1"],
Framed@Graphics[evolfunWide[0.0975], PlotRange -> {{-0.5, 1}, {-0.5, 2.5}}, PlotLabel -> "Spacings\[Rule]2"]
}](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/143fa0d982e878d6.png) |
| Out[175]= | 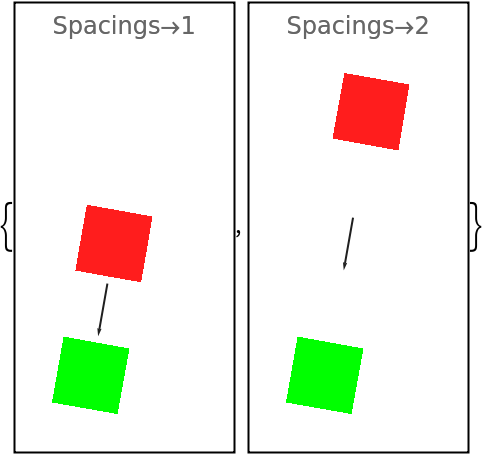 |
Adjust the size of images:
| In[176]:= | ![imgs = {
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{1., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{0.}},"Real32"], "Real32", ColorSpace -> "Grayscale", Interleaving -> None]};
evolfunDefImgs = ResourceFunction["EvolutionViewFunction"][imgs];
Graphics[evolfunDefImgs[0.22], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/4d2e9ac904303042.png) |
| Out[177]= |  |
| In[178]:= |
| Out[179]= |  |
The value of ItemSize is used only when the images are specified as explicit Image, Graphics, or Graphics3D objects:
| In[180]:= | ![prims = {#, Rectangle[-0.3 {1, 1}, 0.3 {1, 1}]} & /@ {Red, Green, Blue, Cyan, Magenta, Black};
graphs = Graphics[{#, Rectangle[-0.3 {1, 1}, 0.3 {1, 1}]}] & /@ {Red, Green, Blue, Cyan, Magenta, Black};
imgs = ConstantImage[#, {1, 1}] & /@ {Red, Green, Blue, Cyan, Magenta,
Black};
Head[imgs[[1]]]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/045225e1ee8f62af.png) |
| Out[181]= |
| In[182]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/a1d4c70d-0652-4a4a-a828-19bcc3533875"]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/0e6603bff7659856.png) |
| Out[183]= |  |
The same holds true for dividers:
| In[184]:= | ![imgs = {
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{1., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{0.}},"Real32"], "Real32", ColorSpace -> "Grayscale", Interleaving -> None]};
divPrims = {Black, Disk[{0, 0}, .3]};
divGraphics = Graphics[{Black, Disk[{0, 0}, .3]}];
divImage = Rasterize[Graphics[{Black, Disk[{0, 0}, .3]}]];
Head[divImage]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/2793dea69828d228.png) |
| Out[185]= |
| In[186]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/489ebb5b-e05f-40b2-981a-41c420798acc"]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/213988cb54b47ee7.png) |
| Out[187]= |  |
Specify the horizontal alignment:
| In[188]:= | ![evolfun = ResourceFunction[
"EvolutionViewFunction"][{
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{1., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{0.}},"Real32"], "Real32", ColorSpace -> "Grayscale", Interleaving -> None]}, Alignment -> Left, Direction -> Left];
Framed@Graphics[{{Dashed, InfiniteLine[{0, 0}, {1, 0}], InfiniteLine[{0, 0}, {0, 1}]}, evolfun[#]}, PlotRange -> 1.5, PlotLabel -> "t = " <> ToString[#]] & /@ {0.02, 0.25, 0.48, 0.70}](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/71f15e28f22010f5.png) |
| Out[189]= | 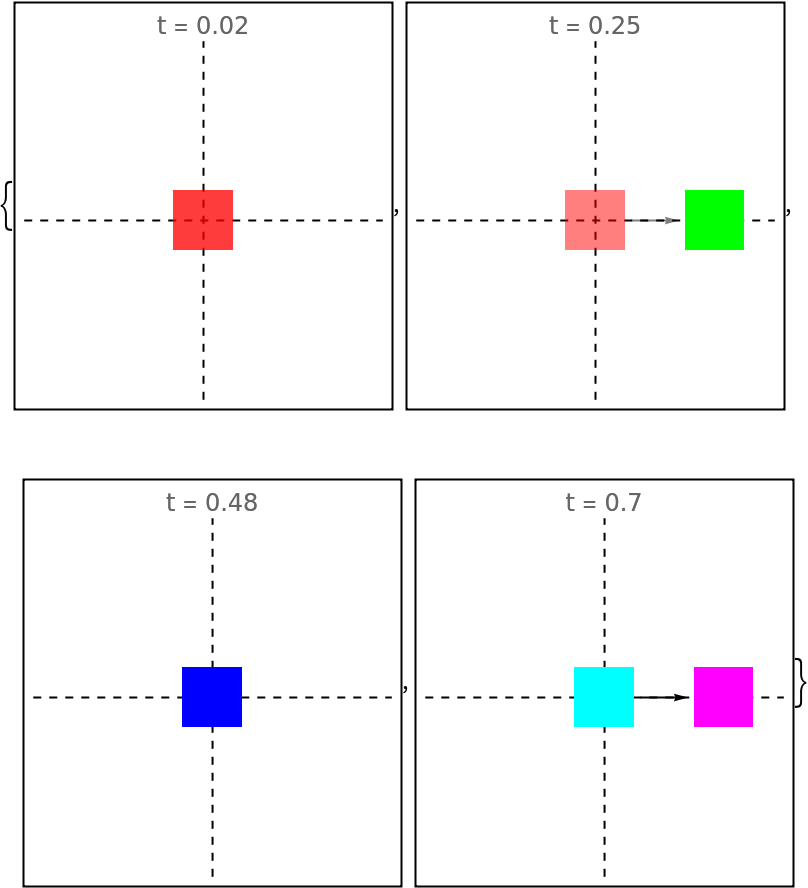 |
Specify the vertical alignment:
| In[190]:= | ![evolfun = ResourceFunction[
"EvolutionViewFunction"][{
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{1., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{0.}},"Real32"], "Real32", ColorSpace -> "Grayscale", Interleaving -> None]}, Alignment -> Top, Direction -> Up];
Framed@Graphics[{{Dashed, InfiniteLine[{0, 0}, {1, 0}], InfiniteLine[{0, 0}, {0, 1}]}, evolfun[#]}, PlotRange -> 1.5, PlotLabel -> "t = " <> ToString[#]] & /@ {0.02, 0.25, 0.48, 0.70}](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/11e14cb697224129.png) |
| Out[191]= | 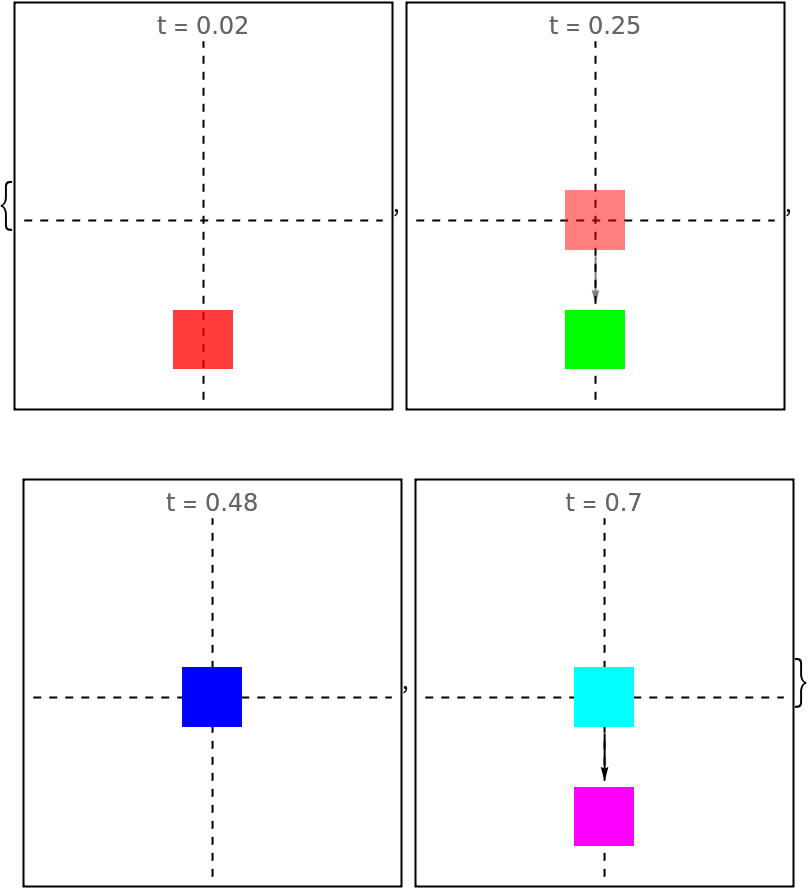 |
Specify both the horizontal and vertical alignment:
| In[192]:= | ![evolfun = ResourceFunction[
"EvolutionViewFunction"][{
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{1., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{0.}},"Real32"], "Real32", ColorSpace -> "Grayscale", Interleaving -> None]}, Alignment -> {Left, Top}, Direction -> 30 Degree];
Framed@Graphics[{{Dashed, InfiniteLine[{0, 0}, {1, 0}], InfiniteLine[{0, 0}, {0, 1}]}, evolfun[#]}, PlotRange -> 1.5, PlotLabel -> "t = " <> ToString[#]] & /@ {0.02, 0.25, 0.48, 0.70}](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/5552f94db082285a.png) |
| Out[193]= | 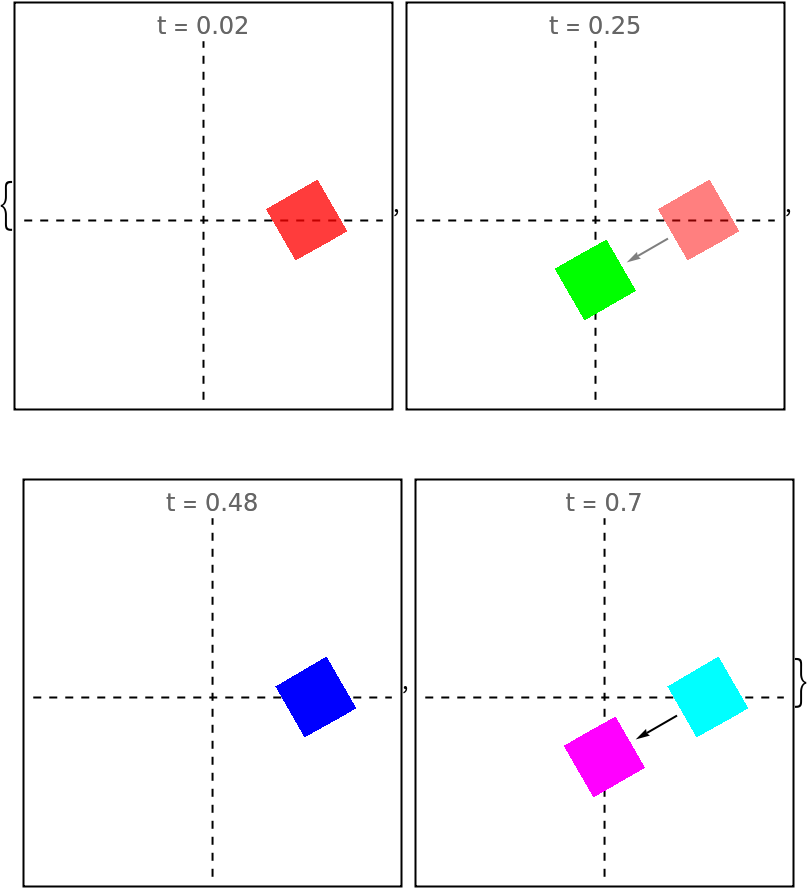 |
Center the objects:
| In[194]:= | ![evolfun = ResourceFunction[
"EvolutionViewFunction"][{
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{1., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{0.}},"Real32"], "Real32", ColorSpace -> "Grayscale", Interleaving -> None]}, Alignment -> {Center, Center}, Direction -> 30 Degree];
Framed@Graphics[{{Dashed, InfiniteLine[{0, 0}, {1, 0}], InfiniteLine[{0, 0}, {0, 1}]}, evolfun[#]}, PlotRange -> 1.5, PlotLabel -> "t = " <> ToString[#]] & /@ {0.02, 0.25, 0.48, 0.70}](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/1104d304b0a03722.png) |
| Out[195]= | 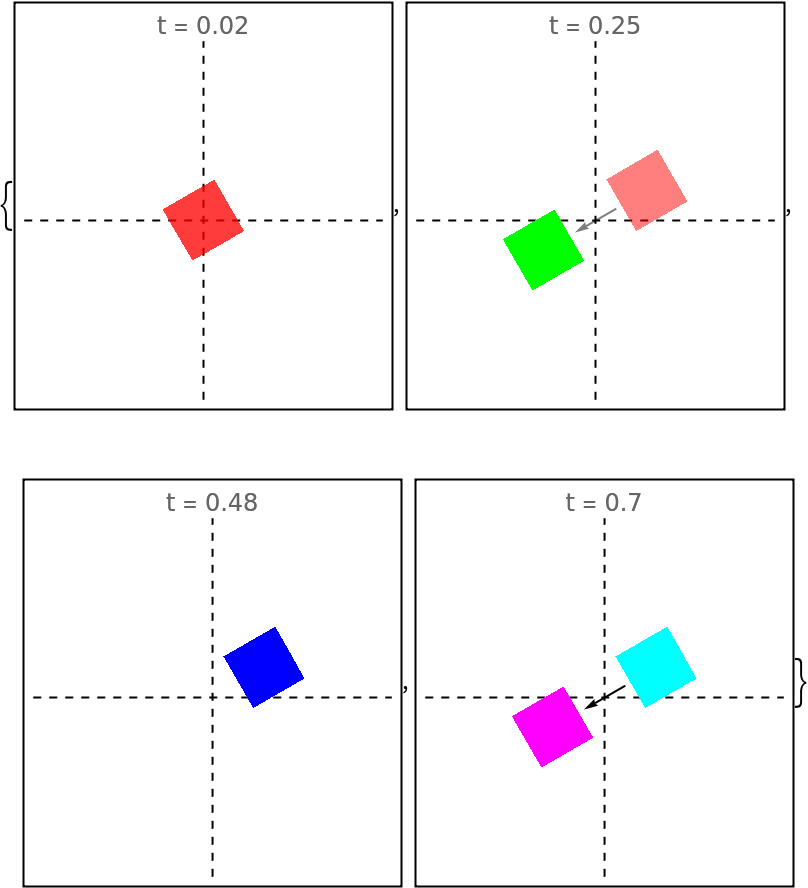 |
Specify the horizontal direction in which the sliding objects move:
| In[196]:= | ![dirs = {Right, Left};
evolfunsDir = ResourceFunction[
"EvolutionViewFunction"][{
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{1., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{0.}},"Real32"], "Real32", ColorSpace -> "Grayscale", Interleaving -> None]}, Direction -> #] & /@ dirs;
gr[f_, times_] := Framed@Graphics[f[#], PlotRange -> {{-1.5, 1.5}, {-1.5, 1.5}}, PlotLabel -> "t = " <> ToString[NumberForm[N@#, {3, 3}]]] & /@ times
Grid[{Style[#, 20, Bold] & /@ dirs}~Join~
Transpose@
MapThread[gr, {evolfunsDir, {{0.02, 0.2475}, {0.02, 0.2475}}}], Dividers -> {All, False}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/0779f106bb71b485.png) |
| Out[197]= | 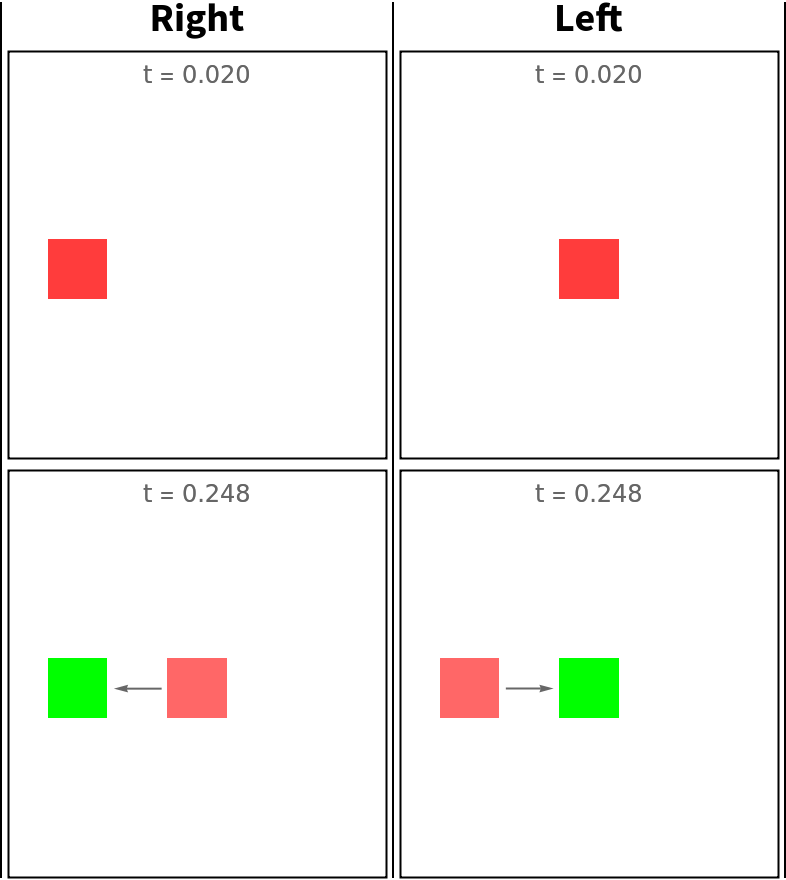 |
Specify the vertical direction:
| In[198]:= | ![dirs = {Up, Down};
evolfunsDir = ResourceFunction[
"EvolutionViewFunction"][{
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{1., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{0.}},"Real32"], "Real32", ColorSpace -> "Grayscale", Interleaving -> None]}, Direction -> #] & /@ dirs;
gr[f_, times_] := Framed@Graphics[f[#], PlotRange -> {{-1.5, 1.5}, {-1.5, 1.5}}, PlotLabel -> "t = " <> ToString[NumberForm[N@#, {3, 3}]]] & /@ times
Grid[{Style[#, 20, Bold] & /@ dirs}~Join~
Transpose@
MapThread[gr, {evolfunsDir, {{0.02, 0.2475}, {0.02, 0.2475}}}], Dividers -> {All, False}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/55333cafadf304dc.png) |
| Out[199]= |  |
An arbitrary direction can be given:
| In[200]:= | ![evolfunsDir = ResourceFunction[
"EvolutionViewFunction"][{
Image[
NumericArray[{{{1., 0., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 0.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{0., 1., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{{1., 0., 1.}}},"Real32"], "Real32", ColorSpace -> "RGB", Interleaving -> True],
Image[NumericArray[{{0.}},"Real32"], "Real32", ColorSpace -> "Grayscale", Interleaving -> None]}, Direction -> 30 Degree];
Grid[Transpose@{{Style["30\[Degree]", 20, Bold]}~
Join~(Framed@
Graphics[evolfunsDir[#], PlotRange -> {{-1.5, 1.5}, {-1.5, 1.5}}, PlotLabel -> "t = " <> ToString[#]] & /@ {0.02, 0.248})}, Dividers -> {All, False}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/39b4a21723e1ef07.png) |
| Out[201]= |  |
Create a progress indicator:
| In[202]:= | ![progressIndicator = ResourceFunction["EvolutionViewFunction"][
Table[{Gray, Disk[{0, 0}, 0.5]}, 20], {"Constant", 5}, Spacings -> 1.2, Alignment -> Center, "EmergeFunction" -> (Scale[#1, #2] &), "FadeFunction" -> (Scale[#1, #2] &), Dividers -> None];
Animate[Graphics[progressIndicator[t], PlotRange -> {{-5, 5}, {-0.5, 0.5}}], {t, 0, 1}, AnimationRate -> .1]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/599324998d2543cd.png) |
| Out[203]= |  |
Create a graphical representation of a countdown:
| In[204]:= | ![nums = Reverse@
Table[Text[Style[i, 80, Bold, Black], {0, 0}], {i, 9}];
countDown = ResourceFunction["EvolutionViewFunction"][nums, "OneByOne", RotateLabel -> False];
Animate[Graphics[countDown[t]], {t, 0, 1}, AnimationRate -> 0.1]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/19d2d05dc4eecd69.png) |
| Out[205]= |  |
Annotate individual stages of a drawing process:
| In[206]:= | ![times = {
Rational[1, 26],
Rational[2, 13],
Rational[7, 26],
Rational[5, 13],
Rational[1, 2],
Rational[8, 13],
Rational[19, 26],
Rational[11, 13],
Rational[25, 26]};
drawinglines = {{
Line[{{0.314, 0.547}, {0.595, 0.831}}]}, { Line[{{0.314, 0.547}, {0.595, 0.831}}],
Line[{{0.606, 0.82}, {0.875, 0.517}}]}, { Line[{{0.314, 0.547}, {0.595, 0.831}}],
Line[{{0.606, 0.82}, {0.875, 0.517}}],
Line[{{0.825, 0.547}, {0.358, 0.564}}]}, { Line[{{0.314, 0.547}, {0.595, 0.831}}],
Line[{{0.606, 0.82}, {0.875, 0.517}}],
Line[{{0.825, 0.547}, {0.358, 0.564}}],
Line[{{0.375, 0.536}, {0.364, 0.214}}]}, { Line[{{0.314, 0.547}, {0.595, 0.831}}],
Line[{{0.606, 0.82}, {0.875, 0.517}}],
Line[{{0.825, 0.547}, {0.358, 0.564}}],
Line[{{0.375, 0.536}, {0.364, 0.214}}],
Line[{{0.383, 0.211}, {0.814, 0.214}}]}, { Line[{{0.314, 0.547}, {0.595, 0.831}}],
Line[{{0.606, 0.82}, {0.875, 0.517}}],
Line[{{0.825, 0.547}, {0.358, 0.564}}],
Line[{{0.375, 0.536}, {0.364, 0.214}}],
Line[{{0.383, 0.211}, {0.814, 0.214}}],
Line[{{0.825, 0.228}, {0.808, 0.528}}]}, { Line[{{0.314, 0.547}, {0.595, 0.831}}],
Line[{{0.606, 0.82}, {0.875, 0.517}}],
Line[{{0.825, 0.547}, {0.358, 0.564}}],
Line[{{0.375, 0.536}, {0.364, 0.214}}],
Line[{{0.383, 0.211}, {0.814, 0.214}}],
Line[{{0.825, 0.228}, {0.808, 0.528}}],
Line[{{0.783, 0.531}, {0.395, 0.214}}]}, { Line[{{0.314, 0.547}, {0.595, 0.831}}],
Line[{{0.606, 0.82}, {0.875, 0.517}}],
Line[{{0.825, 0.547}, {0.358, 0.564}}],
Line[{{0.375, 0.536}, {0.364, 0.214}}],
Line[{{0.383, 0.211}, {0.814, 0.214}}],
Line[{{0.825, 0.228}, {0.808, 0.528}}],
Line[{{0.783, 0.531}, {0.395, 0.214}}],
Line[{{0.392, 0.539}, {0.831, 0.197}}]}};
drawing[t_] := Piecewise[
Evaluate[Prepend[
Table[{{Thick, drawinglines[[idx]]}, t < times[[idx + 1]]}, {idx, Length[drawinglines]}], {{}, t < First[times]}]], {Thick, drawinglines[[-1]]}]
nums = Table[Text[Style[i, 50, Bold, Black], {0, 0}], {i, 8}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/1e0d63f64fc05259.png) |
| Out[207]= |  |
| In[208]:= | ![numbering = ResourceFunction["EvolutionViewFunction"][
nums, {"IncreaseDecrease", 2}, {{Table[1, 6]}, First[times] {1, 1},
times}, {0.6, 1.0}, Spacings -> .2, Alignment -> Right, "NormalizeTimes" -> True, Dividers -> {Black, Thick, Arrow[0.05 {{-1, 0}, {1, 0}}]}];
Animate[Graphics[{numbering[t], drawing[t]}, PlotRange -> {{0.2, 1}, {0, 1.2}}], {t, 0, 1}, AnimationRate -> .1]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/32b86df909b00004.png) |
| Out[209]= | 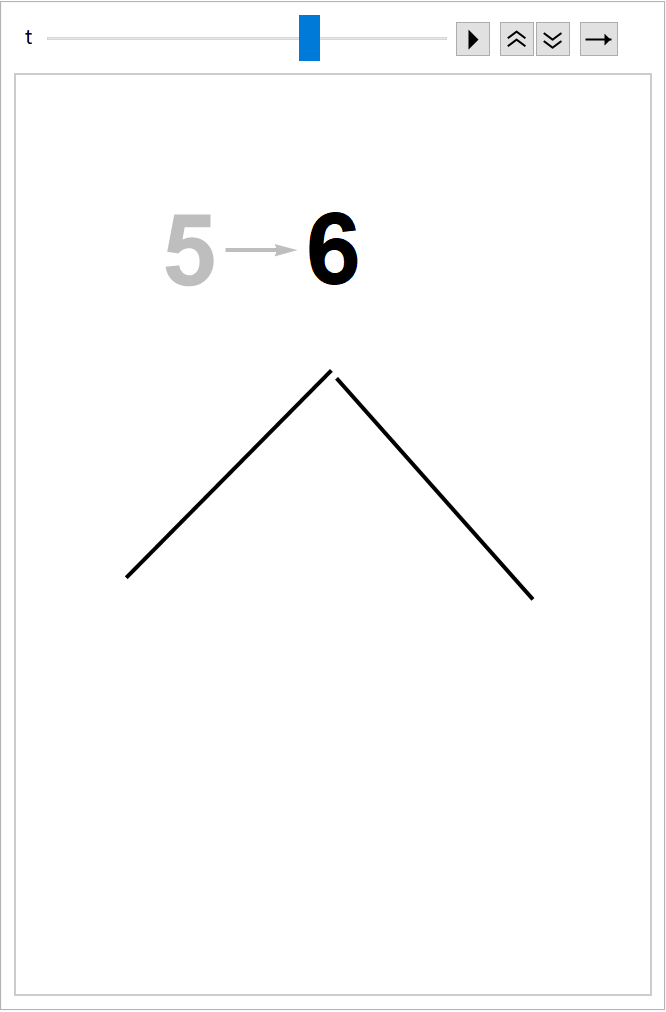 |
When no explicit PlotRange for Graphics is specified, unexpected behavior occurs:
| In[211]:= | ![imgs = {#, Disk[{0, 0}, 0.2]} & /@ {Red, Green, Blue, Cyan, Magenta, Black};
evolf = ResourceFunction["EvolutionViewFunction"][imgs];
Animate[Graphics[evolf[t]], {t, 0, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/526032c11256db67.png) |
| Out[212]= | 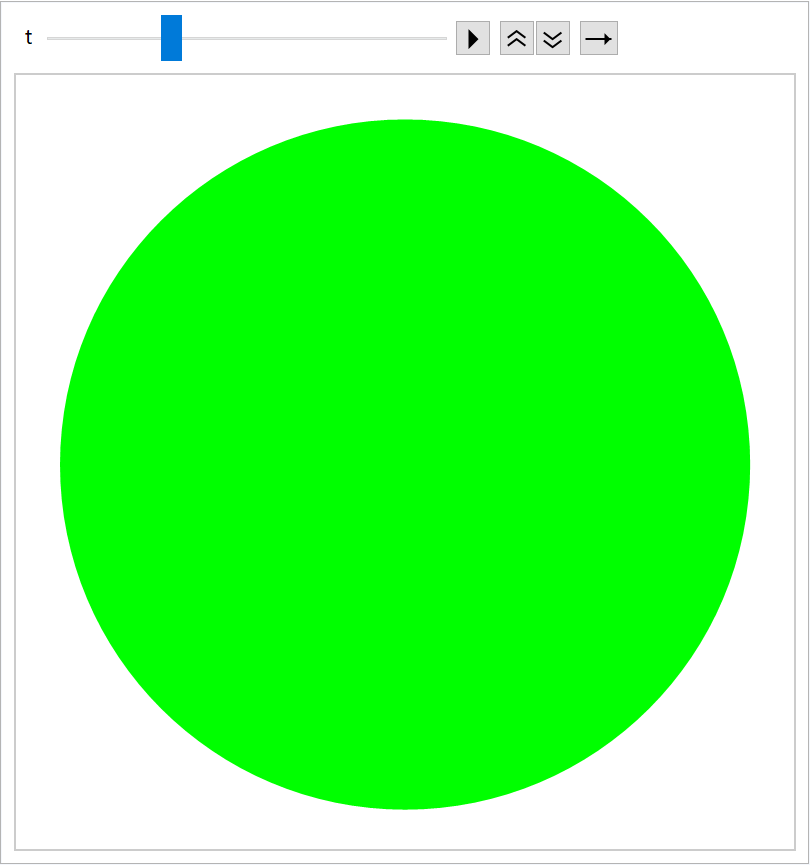 |
Specify PlotRange explicitly:
| In[213]:= |
| Out[213]= |  |
When no color setting is given, the default fade and emerge functions do not work:
| In[214]:= | ![evolfunDefCol = ResourceFunction["EvolutionViewFunction"][
Table[Disk[{0, 0}, 0.2], 4]];
Framed@Graphics[evolfunDefCol[#], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[#]] & /@ Subdivide[0, 0.03, 3]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/2199e8d1f54409be.png) |
| Out[215]= |  |
Specify color explicitly:
| In[216]:= | ![evolFunBlack = ResourceFunction["EvolutionViewFunction"][
Table[{Black, Disk[{0, 0}, 0.2]}, 4]];
Framed@Graphics[evolFunBlack[#], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[#]] & /@ Subdivide[0, 0.03, 3]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/30be889903d68f00.png) |
| Out[217]= |  |
When explicit timestamps are used, the option "NormalizeTimes" is ignored:
| In[218]:= | ![imgs = {{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}};
evolfunExplicit = ResourceFunction["EvolutionViewFunction"][imgs, Automatic, {Table[1, 6], {1, 1}, {1, 2, 3, 4}}, "NormalizeTimes" -> True];
Framed@Graphics[evolfunExplicit[#], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[N@#]] & /@ Subdivide[5]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/117bbe0024be09ee.png) |
| Out[219]= | 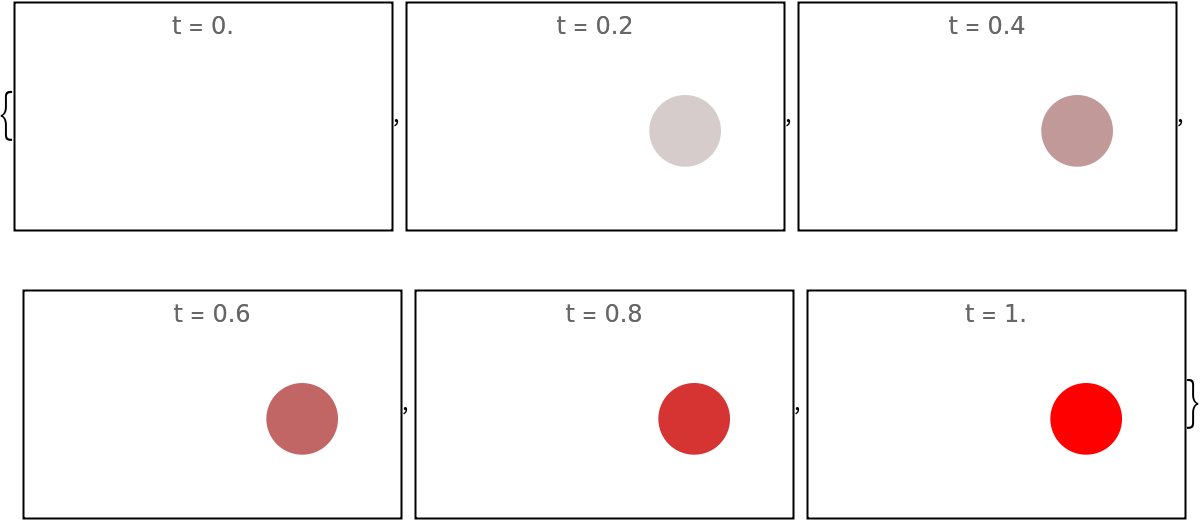 |
The time span of the latter function is 5 in this case:
| In[220]:= |
| Out[220]= | 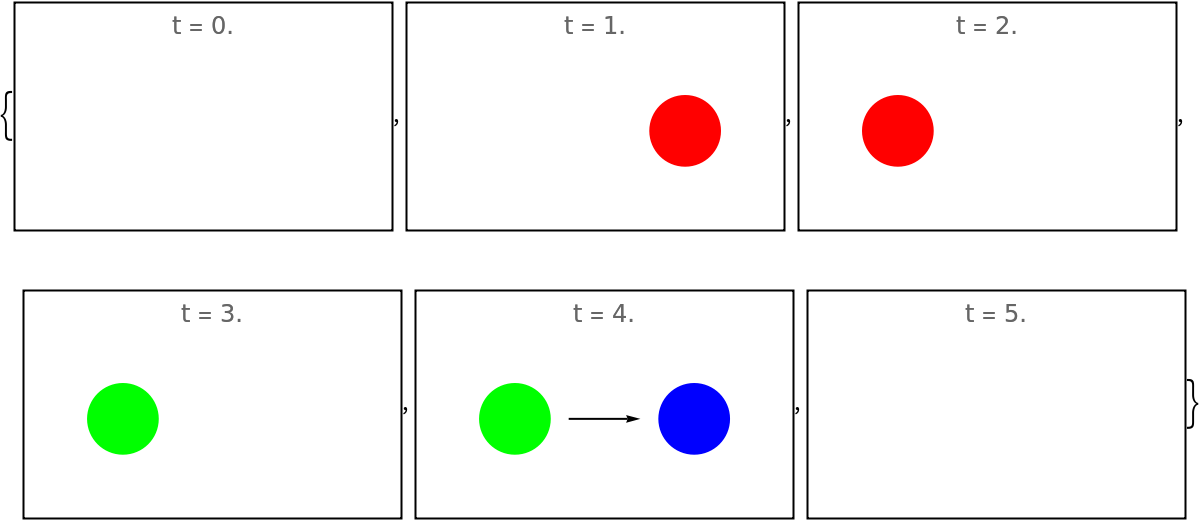 |
Compare with the default setting:
| In[221]:= | ![evolfunNotExpl = ResourceFunction["EvolutionViewFunction"][imgs, Automatic, {Table[1, 6], {1, 1}}, "NormalizeTimes" -> True];
Framed@Graphics[evolfunNotExpl[#], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[N@#]] & /@ Subdivide[5]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/3484874e8fb13e75.png) |
| Out[222]= | 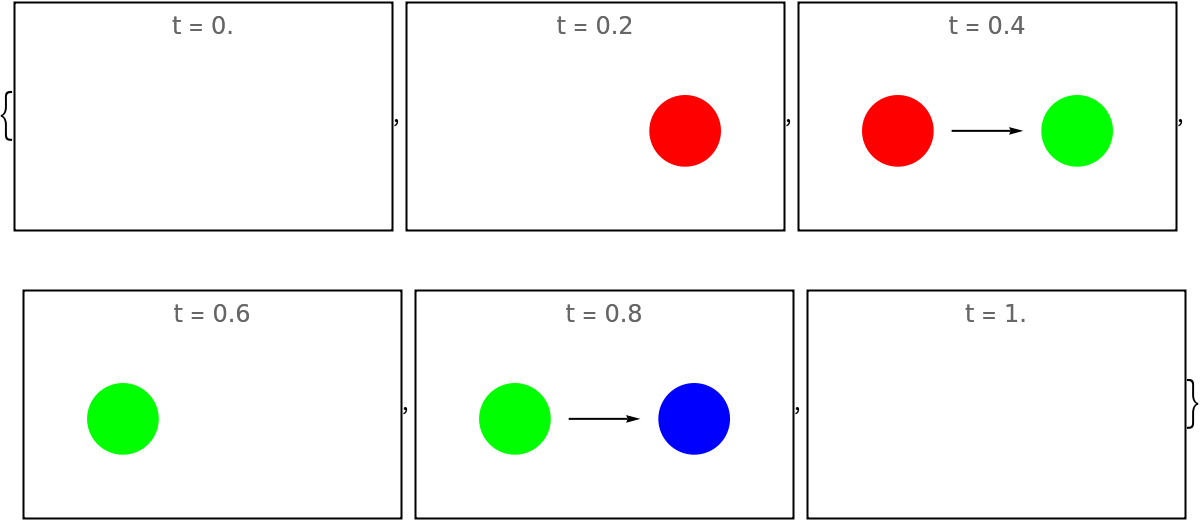 |
When the option Verbose is set to True, the output is not a function but an Association containing a parameter summary:
| In[223]:= | ![imgs = {{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}};
out = ResourceFunction["EvolutionViewFunction"][imgs, Verbose -> False];
Head[out]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/64f25ead05a09143.png) |
| Out[224]= |
| In[225]:= |
| Out[226]= |
| In[227]:= |
| Out[227]= | 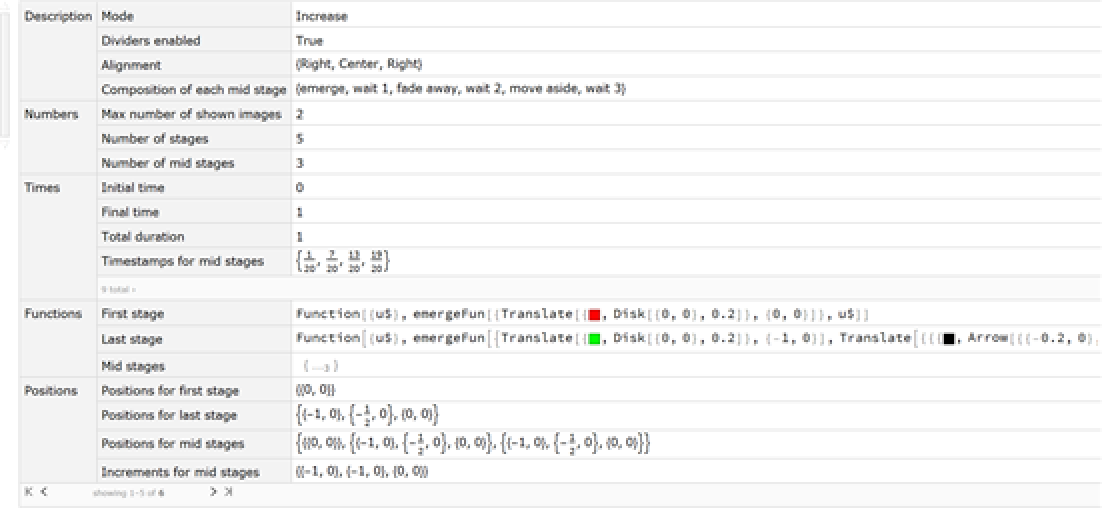 |
To improve formatting, some parameters in the summary Association are wrapped in HoldForm:
| In[228]:= |
| Out[229]= |
| In[230]:= |
| Out[230]= |
Use ReleaseHold to get the actual values:
| In[231]:= |
| Out[231]= |
For some cases, the second argument for functions in "EmergeFunction" and "FadeFunction" should be conditioned by NumericQ:
| In[232]:= | ![emfun1[gr_, t_] := gr /. col_?ColorQ :> Blend[{col, Blue}, t]
emfun2[gr_, t_?NumericQ] := gr /. col_?ColorQ :> Blend[{col, Blue}, t]
imgs = {{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}};
evolfunNoCond = ResourceFunction["EvolutionViewFunction"][imgs, "EmergeFunction" -> emfun1];](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/6c8f57206ca819f1.png) |
| In[233]:= |
The second argument for functions in "FadeFunction" is automatically reversed and so the same functions can be supplied to "EmergeFunction" as well as "FadeFunction":
| In[234]:= | ![fun[gr_, t_?NumericQ] := Scale[gr, t]
imgs = {{
RGBColor[1, 0, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 1, 0],
Disk[{0, 0}, 0.2]}, {
RGBColor[0, 0, 1],
Disk[{0, 0}, 0.2]}};
evolfunEmerge = ResourceFunction["EvolutionViewFunction"][imgs, "OneByOne", "EmergeFunction" -> fun, "FadeFunction" -> None];
Framed@Graphics[evolfunEmerge[#], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[N@#]] & /@ Subdivide[0, 0.05, 5]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/579dbe5a9868d44b.png) |
| Out[235]= | 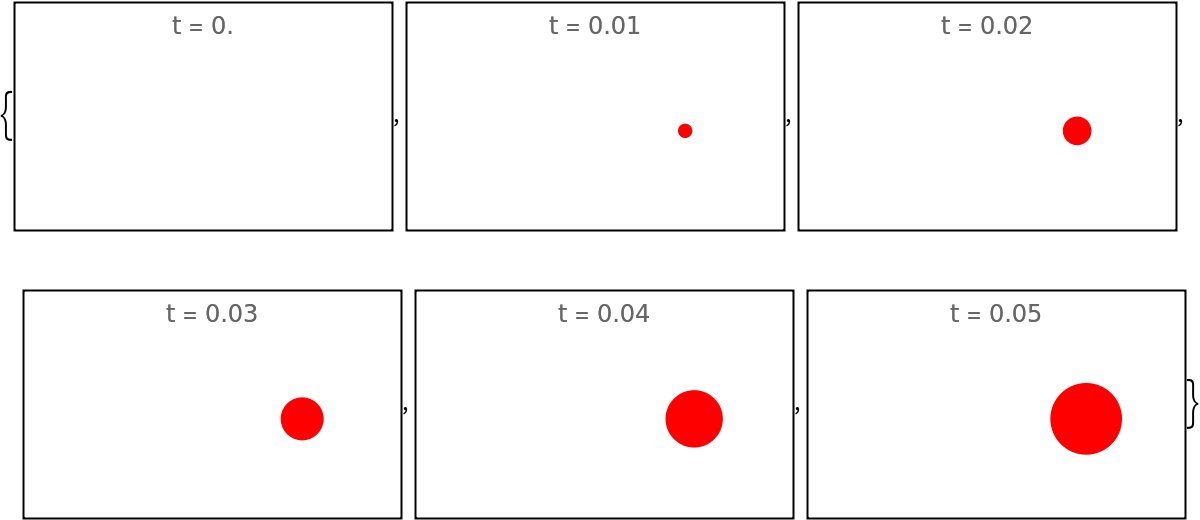 |
| In[236]:= | ![evolfunFade = ResourceFunction["EvolutionViewFunction"][imgs, "OneByOne", "EmergeFunction" -> None, "FadeFunction" -> fun];
Framed@Graphics[evolfunFade[#], PlotRange -> {{-1.5, 0.5}, {-0.5, 0.5}}, PlotLabel -> "t = " <> ToString[N@#]] & /@ Subdivide[0.1, 0.25, 5]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/08c234b6a0c7413f.png) |
| Out[237]= | 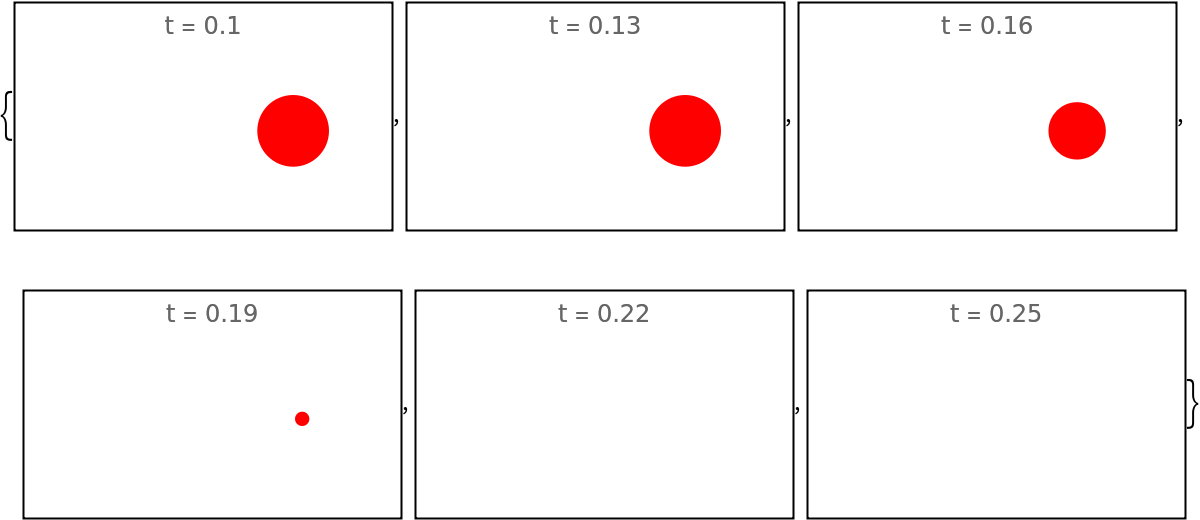 |
Define Translate instead of fade-away-like functions for emergence and fading:
| In[238]:= |
Get the time evolution as well as timing information:
| In[239]:= | ![animation =
ResourceFunction["EvolutionViewFunction"][
Table[Graphics3D[{
Cube[]}, Boxed -> False, ViewProjection -> "Orthographic", SphericalRegion -> True, ViewPoint -> {3.0444, -2.4564, 1.0872}], 15], {"Increase", 4}, {{3, 1, 10, 1, 2, 1}}, {-.5, 0}, "EmergeFunction" -> translateEm, "FadeFunction" -> {translateFa, None}, Dividers -> None, Direction -> 12 Degree, Spacings -> .5, RotateLabel -> False, Alignment -> {Left, Bottom, Right}];
{mids, timestamps} =
Values@ResourceFunction["EvolutionViewFunction"][
Table[1, 15], {"Increase", 4}, {{3, 1, 10, 1, 2, 1}}, Verbose -> True][[
"Times", {"Durations of mid stages", "Timestamps for mid stages"}]];](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/08d4f15b46bf4b83.png) |
Synchronize different parts of the scene:
| In[240]:= | ![cylfun[t_] := Inset[Graphics3D[{
EdgeForm[],
Cylinder[{{0, 0, -1}, {0, 0, 1}}]}, Boxed -> False, ViewProjection -> "Orthographic", SphericalRegion -> True, ViewPoint -> {-1.703, -1.513, 3.361}, ViewVertical -> {-0.892, 0.446, 0.073}], {0.5, 0.5} + Piecewise[{{0, t < timestamps[[4]]}, {Sin[(2 \[Pi])/
Last@Differences[timestamps] (t + Accumulate[mids][[-2]])], t < timestamps[[-2]]}}] ({.75, 0.39} - {0.5, 0.5}), ImageScaled[{1, 1}/2], .6]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/12587b0c447d4626.png) |
Play the animation:
| In[241]:= | ![Animate[Graphics[{Inset[Graphics3D[{
GrayLevel[0.5],
EdgeForm[],
Translate[
Cylinder[{{-0.5, 0, 0}, {0.5, 0, 0}}, 0.1], {{0, 0, 0}, {0, 3, 0}}],
Cuboid[{-0.5, 0, -0.1}, {0.5, 3, 0.1}]}, Boxed -> False, ViewProjection -> "Orthographic", SphericalRegion -> True, ViewPoint -> {3.0444, -2.4564, 1.0872}, ViewAngle -> 0.017453292519943295`, Lighting -> "Neutral"], {0.25, -.1}, ImageScaled[{1, 1}/2], 2.8],
cylfun[t], animation[t], Inset[Graphics3D[{
EdgeForm[],
Cylinder[{{0, 0, -1}, {0, 0, 1}}]}, Boxed -> False, ViewProjection -> "Orthographic", SphericalRegion -> True, ViewPoint -> {3.0444, -2.4564, 1.0872}], {-0.53, 0.7448`}, ImageScaled[{1, 1}/2], 1.1]}, PlotRange -> {{-1.3, 2.5}, {-1, 1}}], {{t, 0.4}, 0, 1, Appearance -> "Labeled"}, AnimationRate -> .02]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/1729fc2a36721b14.png) |
| Out[241]= | 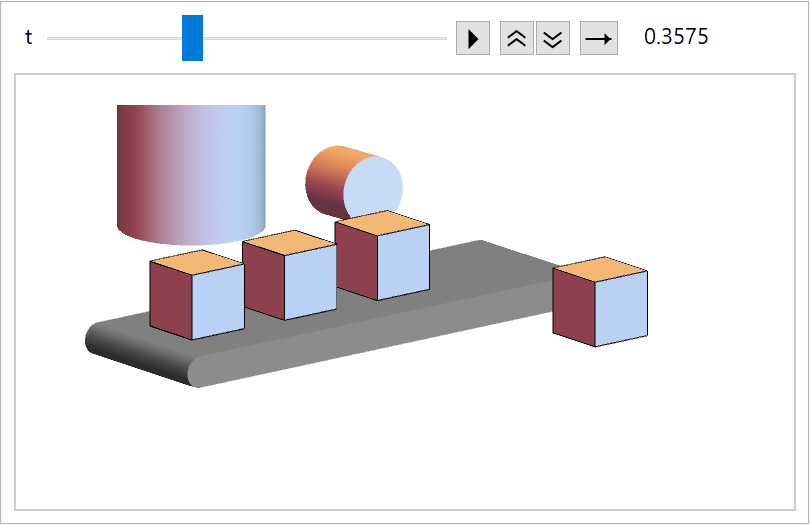 |
Specify lines (create additional nodes by ![]() click):
click):
| In[242]:= | ![lines = {};
initnumpts = 10;
Manipulate[
Graphics[lines = Partition[pt, 2, 1]; Line[pt], PlotRange -> 2], {{pt, CirclePoints[1.5, initnumpts] + RandomReal[0.3 {-1, 1}, {initnumpts, 2}]}, Locator, LocatorAutoCreate -> True}]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/4c245ed6138d4a7a.png) |
| Out[243]= | 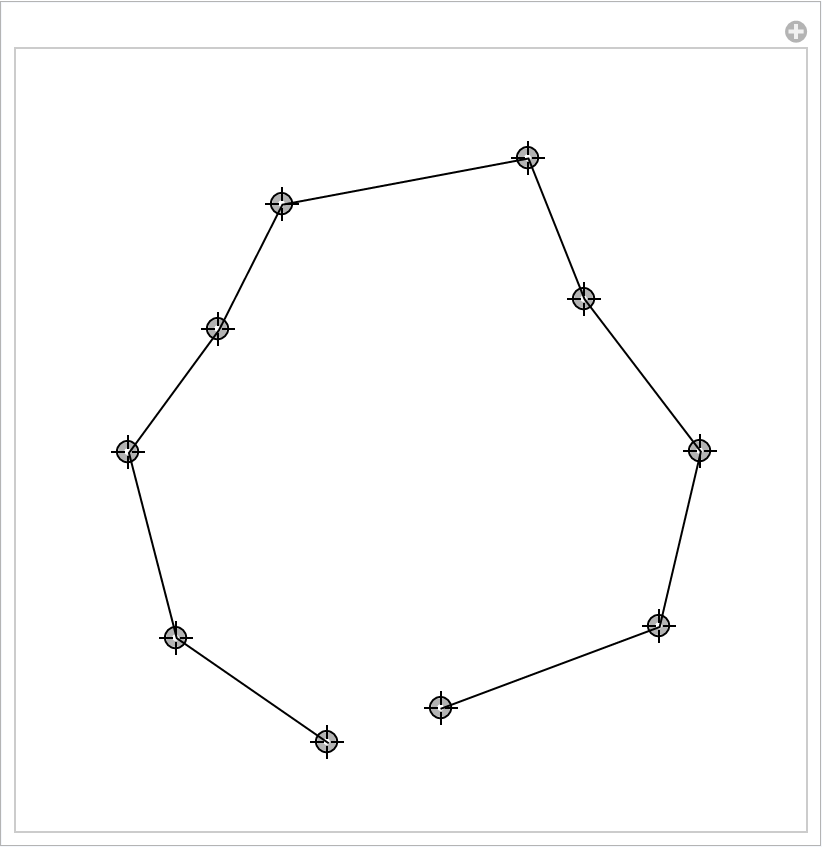 |
Get evolution functions:
| In[244]:= | ![getFun[pos_, dir_, spac_] := ResourceFunction[
"EvolutionViewFunction"][{{
RGBColor[1., 0.472465, 0.0357061],
Disk[{0, 0}, 0.2]}, {
RGBColor[
0.925926, 0.4378416666666667, 0.04721706666666667],
Disk[{0, 0}, 0.2]}, {
RGBColor[
0.8518519999999999, 0.40321833333333335`, 0.05872803333333333],
Disk[{0, 0}, 0.2]}, {
RGBColor[0.777778, 0.368595, 0.070239],
Disk[{0, 0}, 0.2]}, {
RGBColor[
0.5185186666666666, 0.24741358, 0.11052733333333334`],
Disk[{0, 0}, 0.2]}, {
RGBColor[
0.2592593333333333, 0.12623216, 0.15081566666666668`],
Disk[{0, 0}, 0.2]}, {
RGBColor[0., 0.00505074, 0.191104],
Disk[{0, 0}, 0.2]}}, {"Continue", 3}, {{1, 1, 1, 1, 1, 1}, {0.05, 0}},
pos, "EmergeFunction" -> {Automatic, None}, "FadeFunction" -> {None, None}, Dividers -> None, Direction -> dir, Spacings -> spac/(3 - 1), Alignment -> None]
getPars[line_] := Module[{ang},
ang = VectorAngle[{1, 0}, line[[2]] - line[[1]]];
If[Negative@
Last[Cross[{1, 0, 0}, Append[line[[2]] - line[[1]], 0]]], ang *= -1];
{line[[1]], ang, Norm[line[[2]] - line[[1]]]}
]
funs = getFun @@ getPars[#] & /@ lines;](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/069148aaf74c7535.png) |
Get times:
| In[245]:= | ![timestamps = ResourceFunction["EvolutionViewFunction"][
Table[1, 6], {"Continue", 3}, {{1, 1, 1, 1, 1, 1}, {0.05, 0}}, Verbose -> True]["Times", "Timestamps for mid stages"];
times = Range[0, 2 Length[funs], timestamps[[3]]][[;; Length[funs]]];](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/643ab10f15f53959.png) |
Play the animation:
| In[246]:= | ![globfun[t_] := Reverse@MapThread[#1[
Piecewise[{{0, t < #2}, {Rescale[t, {#2, #3}, {0, 1}], t < #3}}, 1]] &, {funs, times, times + 1}]
Animate[Graphics[{Line[lines], globfun[t]}, PlotRange -> 2], {t, 0, Last[times] + 1}, AnimationRate -> .5]](https://www.wolframcloud.com/obj/resourcesystem/images/551/5515de3a-ae1d-4add-9082-2ac57720c5e4/0abe7647f57749b7.png) |
| Out[247]= | 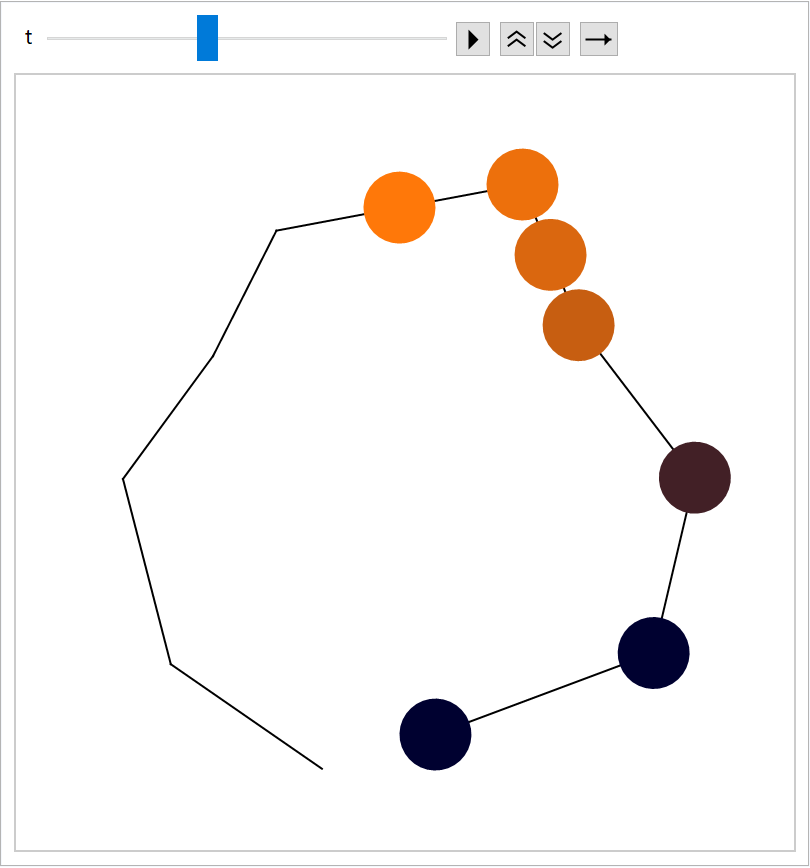 |
This work is licensed under a Creative Commons Attribution 4.0 International License