Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate Euler's false logarithmic series
ResourceFunction["EulerFalseLog"][a,z] gives the false logarithmic series sa(z) of Euler. |
Evaluate numerically:
| In[1]:= |
|
| Out[1]= |
|
Plot over a subset of the reals:
| In[2]:= |
|
| Out[2]= |
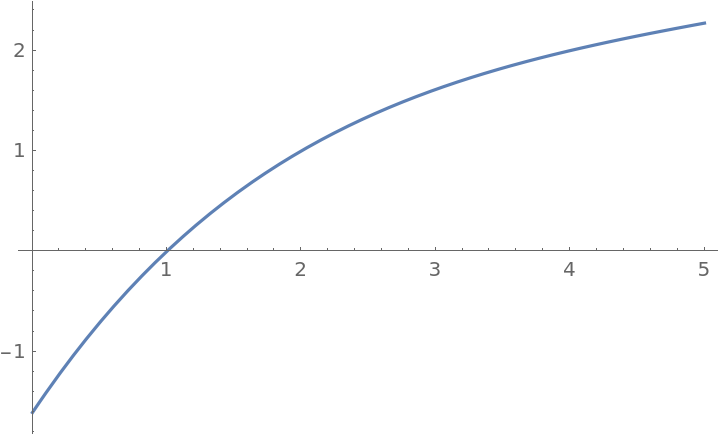
|
Evaluate for complex arguments:
| In[3]:= |
|
| Out[3]= |
|
Evaluate to high precision:
| In[4]:= |
|
| Out[4]= |
|
The precision of the output tracks the precision of the input:
| In[5]:= |
|
| Out[5]= |
|
EulerFalseLog threads elementwise over lists:
| In[6]:= |
|
| Out[6]= |
|
Visualize the difference between Euler's false logarithm and the logarithm:
| In[7]:= |
![Manipulate[
Plot[{ResourceFunction["EulerFalseLog"][a, a^x], Log[a, a^x]}, {x, -2.1, 5}, {Epilog -> {
RGBColor[1, 0, 0],
PointSize[0.01],
Point[{{-2, -2}, {-1, -1}, {0, 0}, {1, 1}, {2, 2}, {3, 3}, {4, 4}, {5,
5}}]}, PlotRange -> {-2.2, 5.5}}], {a, 2, 10, 1, Appearance -> "Labeled"}, SaveDefinitions -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/d93/d9364588-7310-4823-9bdf-8c2b7686e5b1/1b64ed7b2c4da543.png)
|
| Out[7]= |
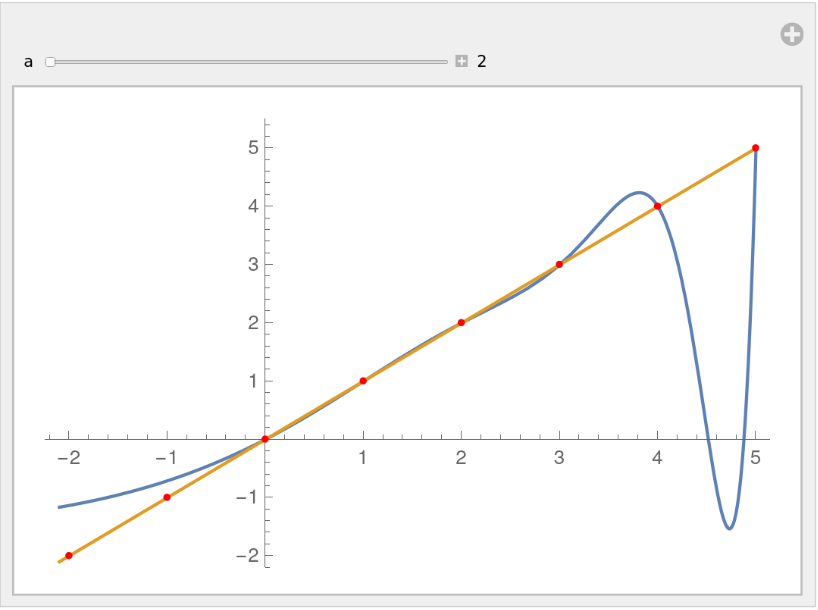
|
EulerFalseLog can be expressed in terms of QPolyGamma for x=0:
| In[8]:= |
|
| Out[8]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License