Wolfram Research

Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 DominatingIntegerPartitionQ (1.0.0) current version: 1.0.1 »

Source Notebook

Find out if one partition of an integer dominates another

Contributed by: Wolfram Staff (original content by Sriram V. Pemmaraju and Steven S. Skiena)

ResourceFunction["DominatingIntegerPartitionQ"][p,q]

yields True if integer partition p dominates integer partition q and False otherwise.

Details and Options

For two integer partitions p={p1,…,pk} and q={q1,…,kl} of some positive integer n, p is said to dominate q if the sum of the t largest parts of p is greater than or equal to the sum of the t largest parts of q, p1+…+pt≥q1+…+qt, for all t≥1, where the partition with fewer parts is padded with zeros at the end.
Partions p and q can be incomparable with respect to dominance.

Examples

Basic Examples (2) 

Since 5+1<4+3, the first partition does not dominate the second:

In[1]:=
ResourceFunction[ "DominatingIntegerPartitionQ"][{5, 1, 1, 1}, {4, 3, 1}]
Out[1]=

The first partition dominates the second since 4≥4, 4+4≥4+3 and 4+4≥4+3+1:

In[2]:=
ResourceFunction["DominatingIntegerPartitionQ"][{4, 4}, {4, 3, 1}]
Out[2]=

Applications (1) 

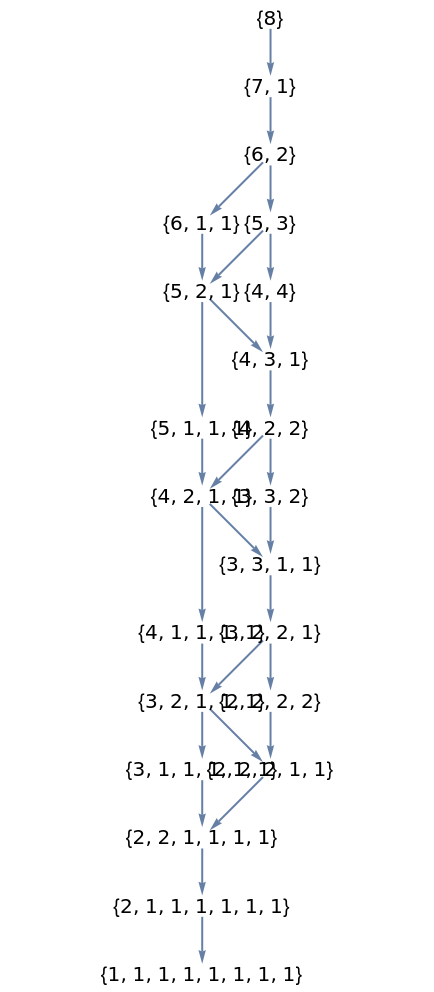
Display the domination lattice on integer partitions, using the resource function HasseDiagram:

In[3]:=
dominationLattice[n_, opts___] := ResourceFunction[ ResourceObject[<|"Name" -> "HasseDiagram", "ShortName" -> "HasseDiagram", "UUID" -> "3836543c-c3fa-422c-99b1-cdeaac2008df", "ResourceType" -> "Function", "Version" -> "1.0.0", "Description" -> "Construct a Hasse diagram of a poset", "RepositoryLocation" -> URL[ "https://www.wolframcloud.com/objects/resourcesystem/api/1.0"], "SymbolName" -> "FunctionRepository`$00e649b9cc5e454c84ad7165f1a59f30`HasseDiagram", "FunctionLocation" -> CloudObject[ "https://www.wolframcloud.com/obj/ff835ddf-f12d-4553-844d-5be7b613b815"]|>, ResourceSystemBase -> Automatic]][ResourceFunction[ "DominatingIntegerPartitionQ"], IntegerPartitions[n], opts, VertexShapeFunction -> "Name"]
In[4]:=
dominationLattice[8]
Out[4]=

Properties and Relations (3) 

DominatingIntegerPartitionQ[p,q] being False does not imply that DominatingIntegerPartitionQ[q,p] is True, in this case because the first element of q is smaller than the first element of p:

In[5]:=
p = {5, 1, 1, 1}; q = {4, 3, 1};
In[6]:=
ResourceFunction["DominatingIntegerPartitionQ"][p, q]
Out[6]=
In[7]:=
ResourceFunction["DominatingIntegerPartitionQ"][q, p]
Out[7]=

DominatingIntegerPartitionQ[p,q] and DominatingIntegerPartitionQ[q,p] can both yield True for certain p and q:

In[8]:=
p = q = {5, 1, 1, 1}
Out[8]=
In[9]:=
ResourceFunction["DominatingIntegerPartitionQ"][p, q]
Out[9]=
In[10]:=
ResourceFunction["DominatingIntegerPartitionQ"][q, p]
Out[10]=

Among the partitions of n, {n} is always the largest and {1,…,1} is the smallest:

In[11]:=
n = 8;
In[12]:=
{First[#], Last[#]} &@ Sort[IntegerPartitions[n], ResourceFunction[ "DominatingIntegerPartitionQ"]]
Out[12]=

Version History

  • 1.0.1 – 31 January 2022
  • 1.0.0 – 28 July 2020

Related Resources

License Information