Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Construct a Hasse diagram of a poset
ResourceFunction["HasseDiagram"][f,s] constructs a Hasse diagram of the partial order set (poset) defined by the binary relation f and set s. |
The Hasse diagram of the set of all subsets of a three-element set, ordered by inclusion:
| In[1]:= |
| Out[1]= | 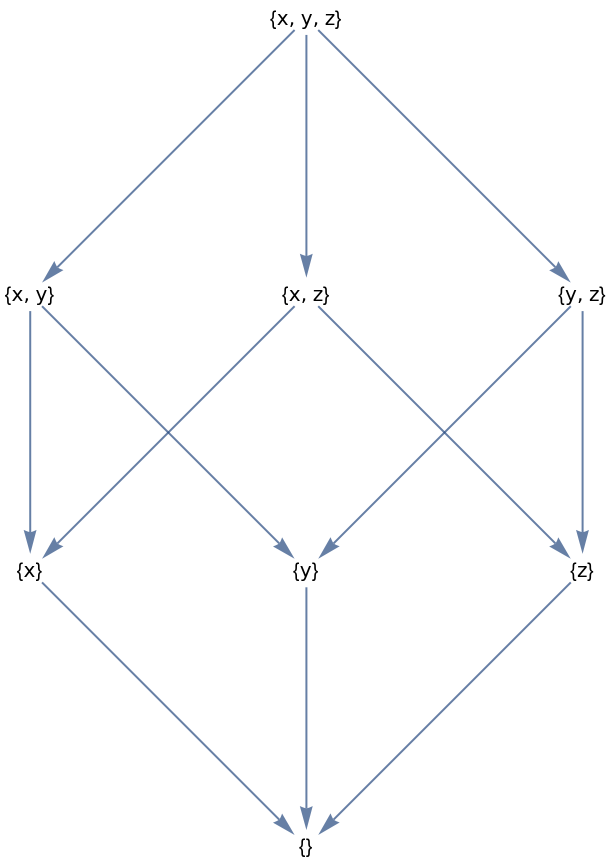 |
Permutations differing by one transposition, ordered by the number of inversions:
| In[2]:= | ![ResourceFunction[
"HasseDiagram"][(Count[#1 - #2, 0] == 2 && ResourceFunction["InversionCount"][#1] > ResourceFunction["InversionCount"][#2]) &, Permutations[{1, 2, 3, 4}], VertexShapeFunction -> "Name"]](https://www.wolframcloud.com/obj/resourcesystem/images/383/3836543c-c3fa-422c-99b1-cdeaac2008df/5b47302277b900d5.png) |
| Out[2]= |  |
Positive integers ordered by divisibility:
| In[3]:= |
| Out[3]= | 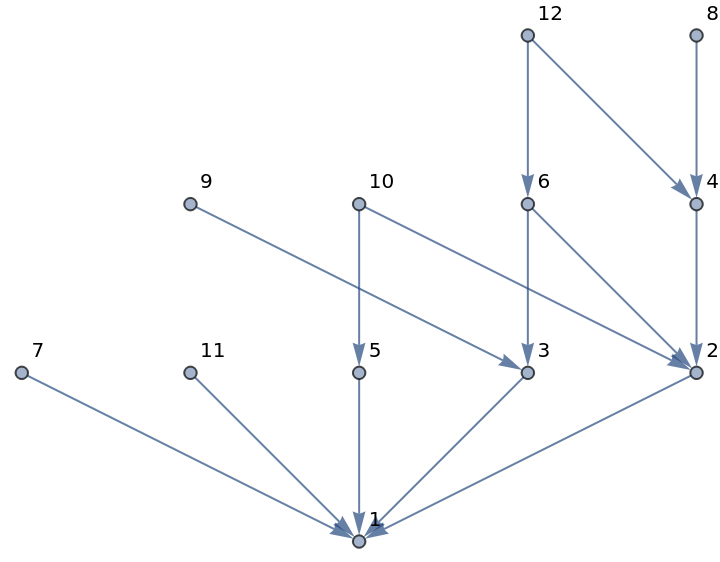 |
Display the domination lattice on integer partitions using the resource function DominatingIntegerPartitionQ:
| In[4]:= |
| In[5]:= | ![dominationLattice[n_, opts___] := ResourceFunction["HasseDiagram"][
ResourceFunction["DominatingIntegerPartitionQ"], IntegerPartitions[n], opts, VertexShapeFunction -> "Name"]](https://www.wolframcloud.com/obj/resourcesystem/images/383/3836543c-c3fa-422c-99b1-cdeaac2008df/405e372241a44b61.png) |
| In[6]:= |
| Out[6]= | 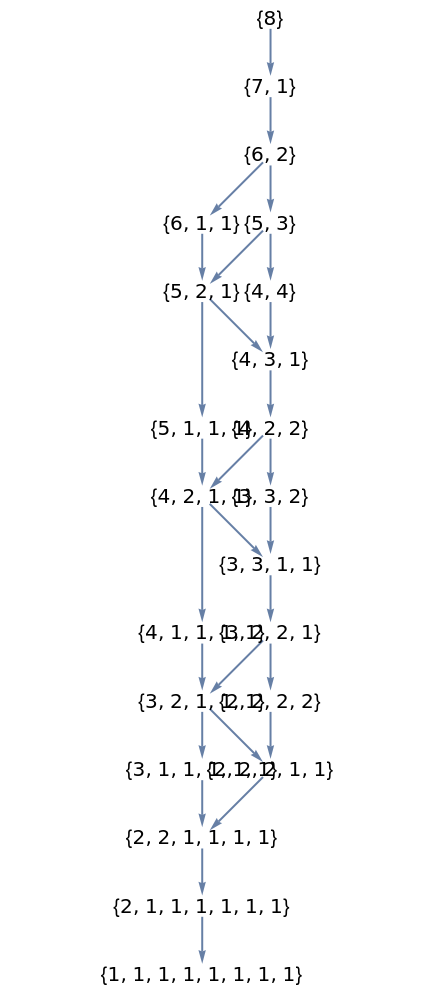 |
This work is licensed under a Creative Commons Attribution 4.0 International License