Basic Examples (4)
Combine the powers in an expression:
Combine powers with multiple terms:
Combine radicals:
DisplayPowersTogether also combines products and quotients that include CubeRoot:
Scope (9)
DisplayPowersTogether combines exponents using the default assumptions stored in $Assumptions. The assumptions in this example are sufficient to combine all the exponents:
DisplayPowersTogether similarly combines all the exponents when 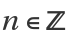 is given as a second argument in DisplayPowersTogether:
is given as a second argument in DisplayPowersTogether:
Provide assumptions allowing some but not all exponents to be combined:
Set $Assumptions as a>0, and specify d>0 as an assumption within DisplayPowersTogether:
Only assume d > 0:
The following assumptions are sufficient to combine all the exponents even though nothing is assumed about b or z:
FullSimplify verifies that DisplayPowersTogether performed a valid transformation under the given assumptions:
This performs independent verification by searching for a counterexample to the previous example. The identity is True in every case considered:
In this case, nothing is assumed and none of the exponents can be combined:
DisplayPowersTogether determines this can be done with a single Sqrt:
Surd is a generalization of CubeRoot. DisplayPowersTogether combines expressions involving Surd when appropriate:
Properties and Relations (2)
Rather than use $Assumptions or DisplayPowersTogether[expr,assum], assumptions can be provided using Assuming:
Two examples are given here where Simplify can combine a sum of terms:
DisplayPowersTogether does not handle sums or differences:
Possible Issues (2)
The result of DisplayPowersTogether has a Head of Defer:
It is not a readily-computable expression:
First can be used to compute on the results:
Alternatively, copy the output shown previously and evaluate it to perform the computation:
DisplayPowersTogether can be used again to ensure the square roots are combined again:
The next example is not in a form that allows DisplayPowersTogether to combine factors:
When the cube root above is distributed across the sum, DisplayPowersTogether can combine factors:
![ResourceFunction["DisplayPowersTogether"][
1 + (x 2^(3/4))/(Sqrt[5] 3^(1/4))]](https://www.wolframcloud.com/obj/resourcesystem/images/c1c/c1c557fd-ff5e-48d6-a9a1-6636824c73c4/4f4f71499cff295a.png)
![ResourceFunction["DisplayPowersTogether"][1 + Sqrt[2/3] Sqrt[1/z]]](https://www.wolframcloud.com/obj/resourcesystem/images/c1c/c1c557fd-ff5e-48d6-a9a1-6636824c73c4/2e25451c40521cd5.png)
![]() is given as a second argument in DisplayPowersTogether:
is given as a second argument in DisplayPowersTogether:![And @@ With[{b = Rationalize[RandomComplex[{-2 - 2 I, 2 + 2 I}], 0.001], z = Rationalize[RandomComplex[{-2 - 2 I, 2 + 2 I}], 0.001]},
Flatten@
Table[PossibleZeroQ[(1 + 2 a^z b^z c^-z d^-z) - (1 + 2 ((a b)/(c d))^z)], {a, 1/3, 2, 1/3}, {c, 1/3, 2, 1/3}, {d, 1/3, 2, 1/3}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/c1c/c1c557fd-ff5e-48d6-a9a1-6636824c73c4/6aff21edb03dcce4.png)
![ResourceFunction["DisplayPowersTogether"][
1 + (Sqrt[x - 2] Sqrt[3 - z])/Sqrt[y - 2], x > 4 && y > 4]](https://www.wolframcloud.com/obj/resourcesystem/images/c1c/c1c557fd-ff5e-48d6-a9a1-6636824c73c4/0dd2acf3124362fb.png)
![Simplify[1/Sqrt[4 x] - Sqrt[1/(4 x)], x < 0]](https://www.wolframcloud.com/obj/resourcesystem/images/c1c/c1c557fd-ff5e-48d6-a9a1-6636824c73c4/16c51a36c3122574.png)
![ResourceFunction["DisplayPowersTogether"][1/Sqrt[4 x] - Sqrt[1/(4 x)],
x < 0]](https://www.wolframcloud.com/obj/resourcesystem/images/c1c/c1c557fd-ff5e-48d6-a9a1-6636824c73c4/00ad4348f0bf6572.png)
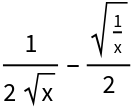
![result = ResourceFunction["DisplayPowersTogether"][1 + Sqrt[2/3] Sqrt[1/z]]](https://www.wolframcloud.com/obj/resourcesystem/images/c1c/c1c557fd-ff5e-48d6-a9a1-6636824c73c4/49319ecc7262a871.png)
![6 + (1 + Sqrt[2/(3 z)])](https://www.wolframcloud.com/obj/resourcesystem/images/c1c/c1c557fd-ff5e-48d6-a9a1-6636824c73c4/5d52991c00e7b68f.png)