Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 UseRealRoots

Source Notebook

Convert all nth roots in an expression, where n is an odd integer, to their real-valued nth roots

Contributed by: Dennis M Schneider

ResourceFunction["UseRealRoots"][expr]

converts all nth roots in expr, where n is an odd integer, to their real-valued nth roots. Otherwise, it uses the principal roots in expr.

Details and Options

In effect, ResourceFunction["UseRealRoots"][expr] replaces every occurrence of Power that involves an odd integer root of a real number with an equivalent expression using Surd.
ResourceFunction["UseRealRoots"] allows the user to use standard mathematical syntax (e.g. x1/5 in place of Surd[x,5]) when entering expressions.
ResourceFunction["UseRealRoots"][expr] modifies Power when expr is being evaluated. The default behavior of Power is restored after expr is evaluated.

Examples

Basic Examples (6) 

UseRealRoots converts an odd integer root in an expression to an expression using Surd:

In[1]:=
{ResourceFunction["UseRealRoots"][(-1)^(3/5)], ResourceFunction["UseRealRoots"][((-1)^(1/5))^3], ResourceFunction["UseRealRoots"][((-1)^3)^(1/5)]}
Out[1]=

Unlike Surd, UseRealRoots evaluates even roots of negative real numbers:

In[2]:=
Surd[-3, 2]
Out[2]=
In[3]:=
ResourceFunction["UseRealRoots"][(-3)^(1/2)]
Out[3]=

Plot over a subset of the reals (compare this with the corresponding example on the Surd documentation page):

In[4]:=
Plot[ResourceFunction[ "UseRealRoots"][{x, x^(1/3), x^(1/5), x^(1/7)}] // Evaluate, {x, -1, 1}, PlotLegends -> "Expressions"]
Out[4]=

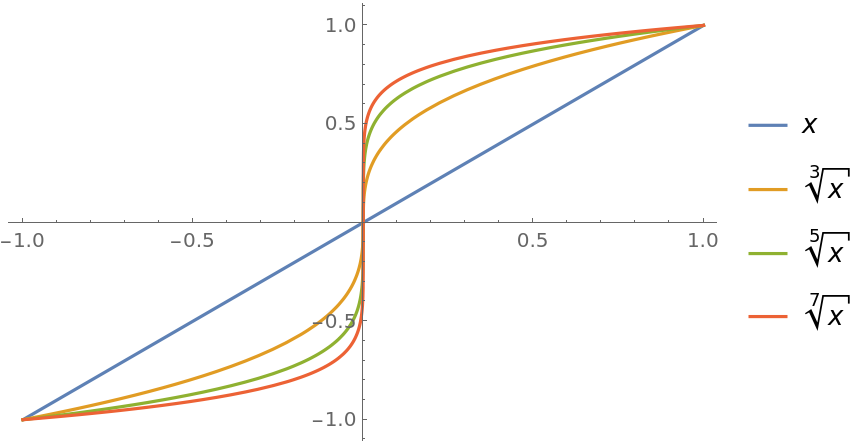
Compare a plot of the function f(x) with UseRealRoots[f(x)]:

In[5]:=
Plot[{Exp[Sin[x]^(1/3)], ResourceFunction["UseRealRoots"][Exp[Sin[x]^(1/3)]]}, {x, -2 \[Pi], 2 \[Pi]}, PlotStyle -> {Thickness[.03], Thickness[.01]}, PlotRange -> All]
Out[5]=

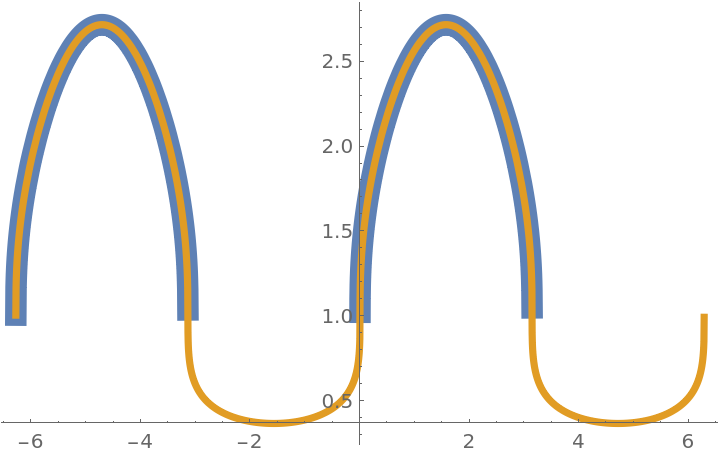
Compare the real and imaginary parts of and UseRealRoots[] over the reals (compare this with the corresponding example on the Surd documentation page):

In[6]:=
ReImPlot[{Power[x, (3)^-1], ResourceFunction["UseRealRoots"][Power[x, (3)^-1]]} // Evaluate, {x, -4, 4}, PlotStyle -> Thickness[.0125], PlotLegends -> Automatic]
Out[6]=

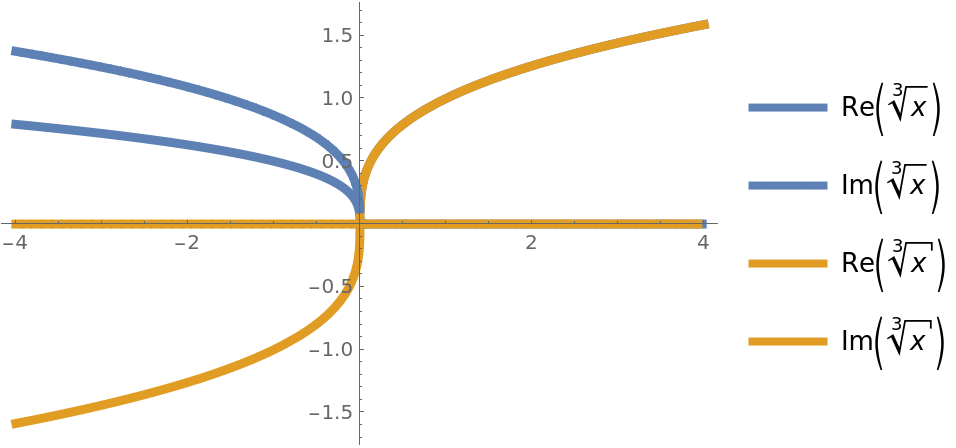
EnhancedPlot automatically incorporates UseRealRoots:

In[7]:=
ResourceFunction["EnhancedPlot"][ Sin[x^(1/3)] + Cos[Sin[Cos[x^(5/3)]]] + Sqrt[1 + x^(2/3)], {x, -3, 3}]
Out[7]=

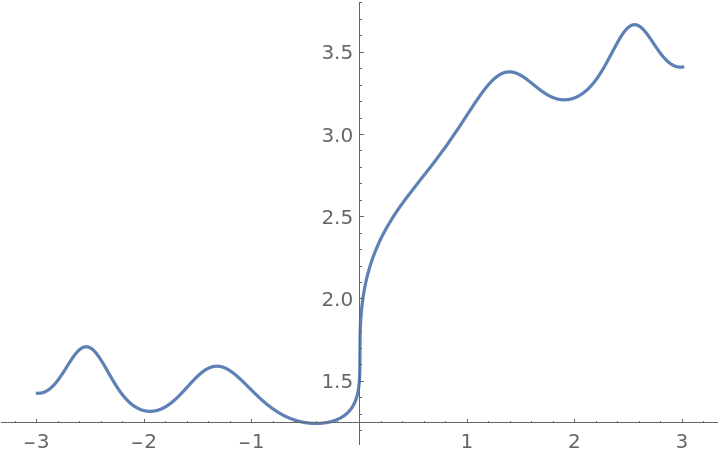
Compare with Plot:

In[8]:=
Plot[ResourceFunction["UseRealRoots"][ Sin[x^(1/3)] + Cos[Sin[Cos[x^(5/3)]]] + Sqrt[1 + x^(2/3)]], {x, -3, 3}]
Out[8]=

Scope (2) 

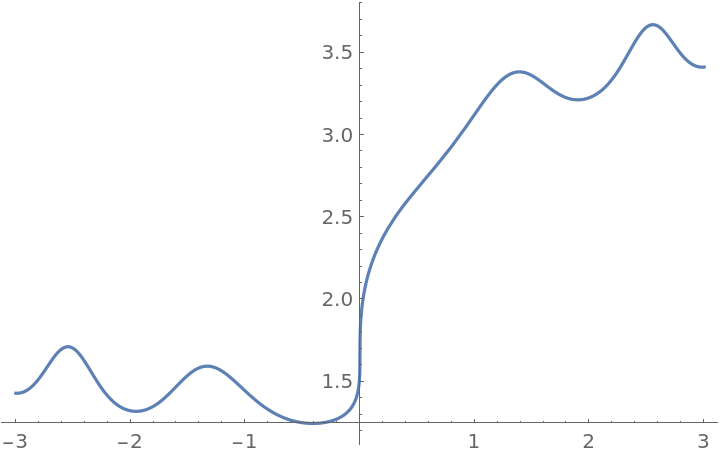
UseRealRoots can be used on any expression and it threads elementwise over lists and matrices:

In[9]:=
ResourceFunction[ "UseRealRoots"][{0^(1/3), (-3/2)^(1/3), (-8)^(1/3), (-Infinity)^( 1/3)}]
Out[9]=
In[10]:=
ResourceFunction[ "UseRealRoots"][{Sin[x] + Sin[x^(-1/3)], Tan[1/Sqrt[1 - x^(4/3)]]}]
Out[10]=
In[11]:=
ResourceFunction["UseRealRoots"][\!\(\* TagBox[ RowBox[{"(", "", GridBox[{ {"1", SuperscriptBox["u", RowBox[{"1", "/", "3"}]]}, { SuperscriptBox[ RowBox[{"(", RowBox[{"-", "1"}], ")"}], RowBox[{"5", "/", "3"}]], RowBox[{ SuperscriptBox["3.375", RowBox[{"1", "/", "5"}]], " "}]} }, GridBoxAlignment->{ "Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.28], { Offset[0.7]}, Offset[0.28]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\)] // MatrixForm
Out[11]=

Use UseRealRoots with FindRoot:

In[12]:=
FindRoot[ResourceFunction["UseRealRoots"][x^(1/3)] == -1.5, {x, 1}]
Out[12]=

Check:

In[13]:=
{x /. %, (-1.5)^3}
Out[13]=

Function Properties  (6) 

UseRealRoots[x1/n] and Surd[x,n] are both defined for all real values when n is an odd positive integer:

In[14]:=
{FunctionDomain[ResourceFunction["UseRealRoots"][x^(1/3)], x], FunctionDomain[Surd[x, 3], x]}
Out[14]=

Compare with Power:

In[15]:=
FunctionDomain[x^(1/3), x]
Out[15]=

For positive even integers n, UseRealRoots[x1/n] and Surd[x,n] are both real-valued for non-negative x:

In[16]:=
{FunctionDomain[ResourceFunction["UseRealRoots"][x^(1/4)], x], FunctionDomain[Surd[x, 4], x]}
Out[16]=

For negative n, UseRealRoots[x1/n] and Surd[x,n] are both defined for all positive x:

In[17]:=
{FunctionDomain[ResourceFunction["UseRealRoots"][x^(-1/4)], x], FunctionDomain[Surd[x, -4], x]}
Out[17]=

UseRealRoots[x1/n] and Surd[x,n] both assume all real values when n is an odd positive integer:

In[18]:=
{FunctionRange[ResourceFunction["UseRealRoots"][x^(1/3)], x, y], FunctionRange[Surd[x, 3], x, y]}
Out[18]=

For positive even integers n, the range of both UseRealRoots[x1/n] and Surd[x,n] is the set of non-negative real numbers:

In[19]:=
{FunctionRange[ResourceFunction["UseRealRoots"][x^(1/4)], x, y], FunctionRange[Surd[x, 4], x, y]}
Out[19]=

For negative odd n, 0 is removed from the range:

In[20]:=
{FunctionRange[ResourceFunction["UseRealRoots"][x^(-1/3)], x, y], FunctionRange[Surd[x, -3], x, y]}
Out[20]=

Differentiation (3) 

The first derivative with respect to x:

In[21]:=
{D[ResourceFunction["UseRealRoots"][x^(1/3)], x], D[Surd[x, 3], x]}
Out[21]=

Higher derivatives of an even root with respect to x using UseRealRoots:

In[22]:=
Table[D[ResourceFunction["UseRealRoots"][x^(1/2)], {x, k}], {k, 1, 3}]
Out[22]=

Higher derivatives of an odd root with respect to x using UseRealRoots:

In[23]:=
derivsFRR = Table[D[ResourceFunction["UseRealRoots"][x^(1/3)], {x, k}], {k, 1, 3}]
Out[23]=

Using Surd:

In[24]:=
derivsS = Table[D[Surd[x, 3], {x, k}], {k, 1, 3}]
Out[24]=

Plot the higher derivatives computed using UseRealRoots:

In[25]:=
Plot[derivsFRR, {x, -4, 4}, PlotLegends -> {"First Derivative", "Second Derivative", "Third Derivative"}]
Out[25]=

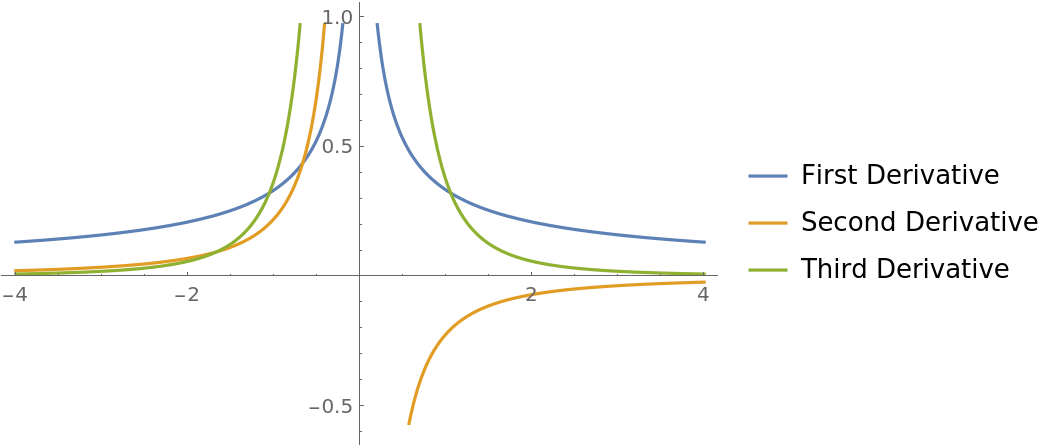
Plot the higher derivatives computed using Surd:

In[26]:=
Plot[derivsS, {x, -4, 4}, PlotLegends -> {"First Derivative", "Second Derivative", "Third Derivative"}]
Out[26]=

Integration (3) 

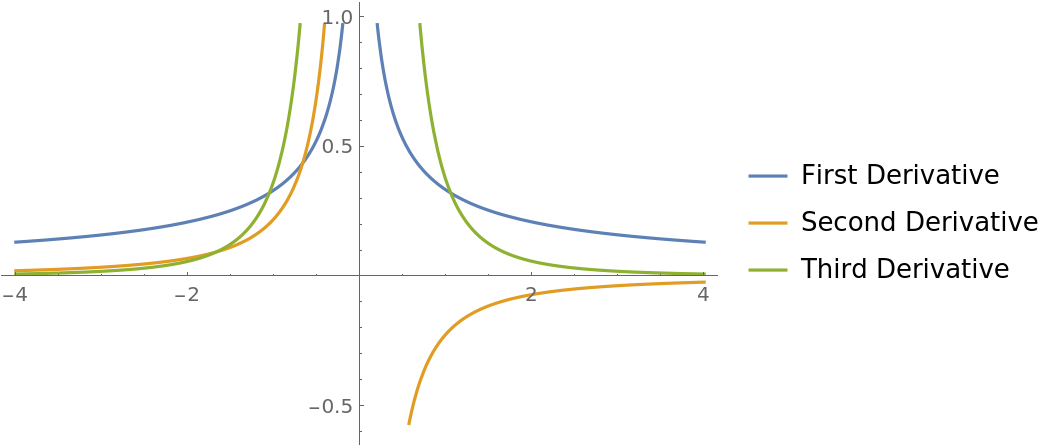
Compute the indefinite integral:

In[27]:=
\[Integral]ResourceFunction["UseRealRoots"][x^(1/2)] \[DifferentialD]x
Out[27]=

Verify by differentiating:

In[28]:=
D[%, x] // FullSimplify
Out[28]=

Definite integral:

In[29]:=
\!\( \*SubsuperscriptBox[\(\[Integral]\), \(-2\), \(-1\)]\(\* InterpretationBox[ TagBox[ FrameBox[ PaneBox[GridBox[{ { StyleBox[ StyleBox[ AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>", BoxBaselineShift->-0.25, BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon", FontColor->RGBColor[ 0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], ShowStringCharacters->False, FontFamily->"Source Sans Pro Black", FontSize->0.65 Inherited, FontWeight->"Heavy", PrivateFontOptions->{"OperatorSubstitution"->False}], StyleBox[ RowBox[{ StyleBox["\<\"UseRealRoots\"\>", "ResourceFunctionLabel", FontFamily->"Source Sans Pro"], " "}], ShowAutoStyles->False, ShowStringCharacters->False, FontSize->0.9 Inherited, FontColor->GrayLevel[0.1]]} }, GridBoxSpacings->{"Columns" -> {{0.25}}}], Alignment->Left, BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False}, BaselinePosition->Baseline, FrameMargins->{{3, 0}, {0, 0}}], Background->RGBColor[0.968627, 0.976471, 0.984314], BaselinePosition->Baseline, DefaultBaseStyle->{}, FrameMargins->{{0, 0}, {1, 1}}, FrameStyle->RGBColor[0.831373, 0.847059, 0.85098], RoundingRadius->4], {"FunctionResourceBox", RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784], "\"UseRealRoots\""}, TagBoxNote->"FunctionResourceBox"], ResourceFunction["UseRealRoots"], BoxID -> "UseRealRoots", Selectable->False][ \*SuperscriptBox[\(x\), \(\(-4\)/3\)]] \[DifferentialD]x\)\)
Out[29]=

An improper integral:

In[30]:=
Integrate[ResourceFunction["UseRealRoots"][x^(-2/3)], {x, -2, 0}]
Out[30]=

Series Expansions (1) 

Find the Taylor expansion using Series:

In[31]:=
Normal@Series[Surd[x, 5], {x, -1, 4}]
Out[31]=
In[32]:=
terms = Normal@ Table[Series[ ResourceFunction["UseRealRoots"][x^(1/5)], {x, -1, m}], {m, 1, 5, 2}]; Plot[{ResourceFunction["UseRealRoots"][x^(1/5)], terms}, {x, -3, 1}, PlotRange -> 2]
Out[33]=

Publisher

Dennis M Schneider

Version History

  • 1.0.0 – 11 September 2020

Related Resources

Author Notes

The formula for the kth derivative of Surd with respect to x is wrong and has been reported to Wolfram Research:

In[1]:=
{D[ResourceFunction["UseRealRoots"][x^(1/2)], {x, k}], D[Surd[x, 2], {x, k}]} // FullSimplify

Check with k=1:

In[2]:=
{x^(1/2 - k) FactorialPower[1/2, k], \!\(\* TagBox[GridBox[{ {"\[Piecewise]", GridBox[{ { RowBox[{"-", FractionBox[ RowBox[{ SuperscriptBox[ RowBox[{"(", RowBox[{"-", FractionBox["1", "x"]}], ")"}], "k"], " ", RowBox[{"Gamma", "[", RowBox[{ RowBox[{"-", FractionBox["1", "2"]}], "+", "k"}], "]"}], " ", RadicalBox["x", "3", MultilineFunction->None, SurdForm->True]}], RowBox[{"2", " ", SqrtBox["\[Pi]"]}]]}], RowBox[{"k", ">=", "1"}]}, { RadicalBox["x", "2", MultilineFunction->None, SurdForm->True], TagBox["True", "PiecewiseDefault", AutoDelete->True]} }, AllowedDimensions->{2, Automatic}, Editable->True, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{1.}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.84]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}, Selectable->True]} }, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{1.}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.35]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "Piecewise", DeleteWithContents->True, Editable->False, SelectWithContents->True, Selectable->False, StripWrapperBoxes->True]\)} /. k -> 1

License Information