Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 DiscreteHilbertTransform

Source Notebook

Compute the discrete Hilbert transform of a list

Contributed by: Jan Mangaldan

ResourceFunction["DiscreteHilbertTransform"][list]

computes the discrete Hilbert transform of a list of real numbers.

Details

The discrete Hilbert transform of a sequence is defined to be the inverse discrete Fourier transform of the termwise product of the discrete Fourier transform of the original sequence and a discrete periodic version of the signum function, multiplied by i.
The Hilbert transform of a sequence has the same amplitude and frequency content as the original sequence. The transform includes phase information that depends on the phase of the original.
In the context of signal processing, the complex sequence zr=ur+i vr obtained from a starting real sequence ur and its discrete Hilbert transform vr is called the "analytic signal". The "analytic signal" has the property of only having the non-negative frequency components of the original sequence.
The list of data supplied to ResourceFunction["DiscreteHilbertTransform"] must be real-valued, but does not need to have a length equal to a power of two.
The list given in ResourceFunction["DiscreteHilbertTransform"][list] can be nested to represent an array of data in any number of dimensions.
The array of data must be rectangular.
If the elements of list are exact numbers, ResourceFunction["DiscreteHilbertTransform"] begins by applying N to them.
ResourceFunction["DiscreteHilbertTransform"] can be used on SparseArray objects.

Examples

Basic Examples (1) 

Compute a discrete Hilbert transform:

In[1]:=
ResourceFunction["DiscreteHilbertTransform"][{1, 1, 2, 2, 1, 1, 0, 0}]
Out[1]=

Scope (2) 

x is a list of real values:

In[2]:=
x = {1, 0, 0, 1, 0, 0, 1};

Compute the Hilbert transform with machine arithmetic:

In[3]:=
ResourceFunction["DiscreteHilbertTransform"][x]
Out[3]=

Compute using 24-digit precision arithmetic:

In[4]:=
ResourceFunction["DiscreteHilbertTransform"][N[x, 24]]
Out[4]=

Compute a 2D Hilbert transform:

In[5]:=
ResourceFunction["DiscreteHilbertTransform"][ RandomReal[{-1, 1}, {3, 6}]]
Out[5]=

Applications (4) 

Generate a sequence composed of two sinusoids with some noise:

In[6]:=
data = Cos[203*2 \[Pi]*Range[0, 1, 0.001]] + Sin[721*2 \[Pi]*Range[0, 1, 0.001]] + RandomVariate[NormalDistribution[0, 0.001], 1001];

Compute the discrete Hilbert transform:

In[7]:=
Short[ht = ResourceFunction["DiscreteHilbertTransform"][data]]
Out[7]=

Visualize the "analytic signal" by separately plotting its real part (the original data) and imaginary part (the Hilbert transform):

In[8]:=
ListLinePlot[{data, ht}, DataRange -> {0, 1}, Joined -> True, PlotLegends -> {"original data", "Hilbert transform"}, PlotRange -> {{0.01, 0.07}, Automatic}]
Out[8]=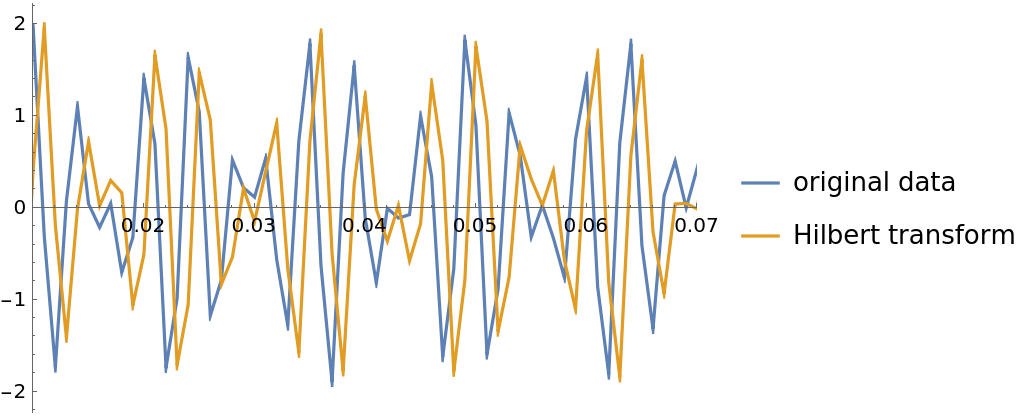

Use the resource function WelchSpectralEstimate to compare the power spectral densities of the original sequence and the "analytic signal":

In[9]:=
ListLogLogPlot[{ResourceFunction["WelchSpectralEstimate"][data, 100.0, "OneSided" -> False], ResourceFunction["WelchSpectralEstimate"][data + I ht, 100.0, "OneSided" -> False]}, Joined -> True, PlotLegends -> {"original PSD", "Hilbert PSD"}]
Out[9]=

Properties and Relations (2) 

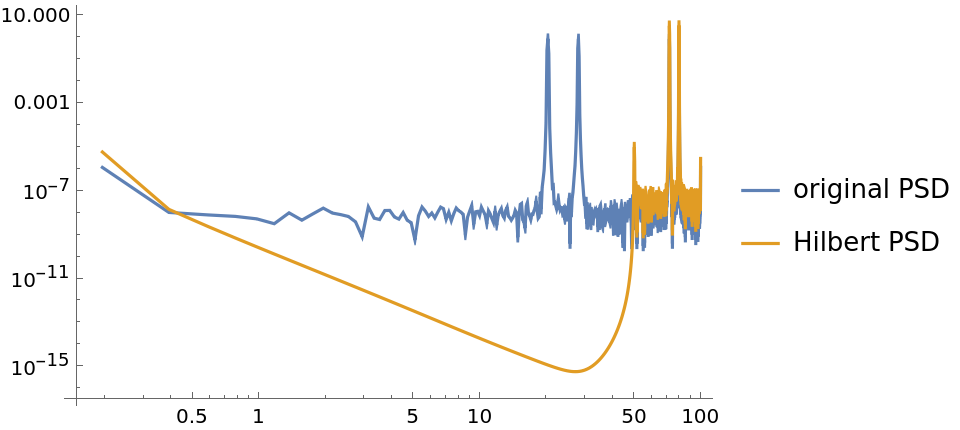A vector of real values:

In[10]:=
x = {1, -2, 1, 2, 1};

Compute its Hilbert transform:

In[11]:=
ht = ResourceFunction["DiscreteHilbertTransform"][x]
Out[11]=

The dot product of the Hilbert transform with the original vector is zero:

In[12]:=
x . ht // Chop
Out[12]=

Compute the discrete Hilbert transform of a vector by multiplying it with the Hilbert transform matrix:

In[13]:=
u = N[{1, 2, 3, 4, 5, 6, 7}]; n = Length[u];
In[14]:=
AbsoluteTiming[ v1 = ResourceFunction["DiscreteHilbertTransformMatrix"][n] . u]
Out[14]=

DiscreteHilbertTransform is faster:

In[15]:=
AbsoluteTiming[v2 = ResourceFunction["DiscreteHilbertTransform"][u]]
Out[15]=
In[16]:=
Chop[v1 - v2]
Out[16]=

Neat Examples (3) 

An even-length sequence:

In[17]:=
v = RandomVariate[NormalDistribution[], 8]
Out[17]=

Use the discrete Hartley transform to compute the discrete Hilbert transform:

In[18]:=
ResourceFunction["DiscreteHartleyTransform"][ RotateRight[ Reverse[ResourceFunction["DiscreteHartleyTransform"][v]]] Join[{0}, ConstantArray[1, Length[v]/2 - 1], {0}, ConstantArray[-1, Length[v]/2 - 1]]]
Out[18]=

Compare with the result of DiscreteHilbertTransform:

In[19]:=
ResourceFunction["DiscreteHilbertTransform"][v]
Out[19]=

Version History

  • 1.0.0 – 13 March 2023

Source Metadata

  • Citation:
    • Čížek V., "Discrete Hilbert Transform." IEEE Transactions on Audio and Electroacoustics, vol. 18, no. 4, 340–343, 1970.
      DOI: 10.1109/TAU.1970.1162139
    • Marple S.L., "Computing the Discrete-Time 'Analytic' Signal via FFT." IEEE Transactions on Signal Processing, vol. 47, no. 9, 2600–2603, 1999.
      DOI: 10.1109/78.782222

Related Resources

License Information