Basic Examples (1)
Compute a discrete Hartley transform:
Scope (4)
x is a list of real values:
Compute the Hartley transform with machine arithmetic:
Compute using 24-digit precision arithmetic:
Compute a complex Hartley transform:
This is equivalent to separately taking the Hartley transforms of the real and imaginary parts:
Compute a 2D Hartley transform:
x is a rank 3 tensor with nonzero diagonal:
Compute the 3D Hartley transform:
Applications (2)
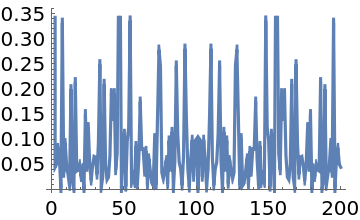
Use the discrete Hartley transform to compute the power spectrum of "white noise":
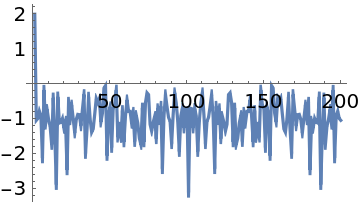
Show the logarithmic spectrum, including the first (DC) component:
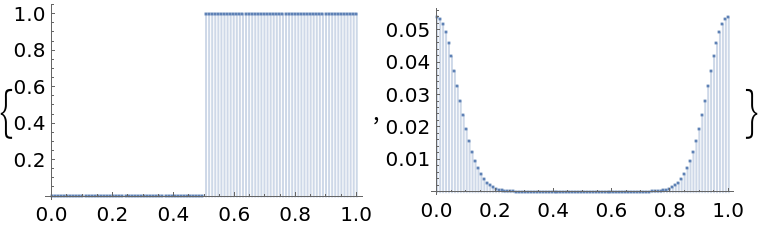
Compute discrete cyclic convolutions to smooth a discontinuous function with a Gaussian:
Compute the cyclic convolution:
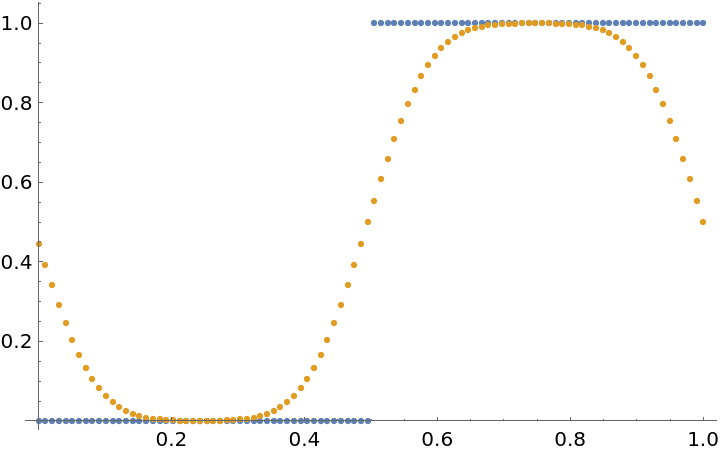
Show the original and smoothed function:
The convolution is consistent with ListConvolve:
Properties and Relations (4)
Compute the discrete Hartley transform from its definition:
DiscreteHartleyTransform is faster:
Compute the discrete Hartley transform of a vector by multiplying it with the Hartley matrix:
DiscreteHartleyTransform is faster:
The discrete Hartley transform is its own inverse:
A list of numbers:
Compute its discrete Hartley transform:
Use the discrete Hartley transform to compute the discrete Fourier transform:
Compare with the result of Fourier:




![dat = RandomReal[1, 200];
fht = ResourceFunction["DiscreteHartleyTransform"][dat];
ListLinePlot[(fht^2 + RotateRight[Reverse[fht]]^2)/2]](https://www.wolframcloud.com/obj/resourcesystem/images/a90/a901ffba-4567-4b6e-975a-98e5aa482ed7/33aa036f3fe5b3dc.png)
![n = 100; dx = 1./(n - 1);
a = Table[UnitStep[x - 1/2], {x, 0, 1, dx}];
b = Table[
If[x <= 1/2, Exp[-100 x^2], Exp[-100 (1 - x)^2]], {x, 0, 1, dx}];
b = b/Total[b];](https://www.wolframcloud.com/obj/resourcesystem/images/a90/a901ffba-4567-4b6e-975a-98e5aa482ed7/65dc9427e4511907.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/711d418b-94f5-4d5a-b950-71d8b55c74c6"]](https://www.wolframcloud.com/obj/resourcesystem/images/a90/a901ffba-4567-4b6e-975a-98e5aa482ed7/35ee8604a15f8e9c.png)
![AbsoluteTiming[v1 = Table[1/Sqrt[n] \!\(TraditionalForm\`
\*UnderoverscriptBox[\(\[Sum]\), \(r = 1\), \(n\)]\*
TemplateBox[{"u", "r"},
"IndexedDefault"]\ \((Cos[
\*FractionBox[\(2 \[Pi]\ \((r - 1)\)\ \((s - 1)\)\), \(n\)]] + Sin[
\*FractionBox[\(2 \[Pi]\ \((r - 1)\)\ \((s - 1)\)\), \(n\)]])\)\), {s, 1, n}]]](https://www.wolframcloud.com/obj/resourcesystem/images/a90/a901ffba-4567-4b6e-975a-98e5aa482ed7/09141a343376f958.png)

