Details
Graph vertices can be thought of as named memory locations for both inputs and outputs.
Evaluation distinguishes inputs as the set of root vertices not pointed to by any directed edge (sources).
All other vertices reached by following directed edges are considered outputs.
A vertex
vi and its edge

are both said to precede another vertex
vj, if the
graph indeed contains edge

.
Values (or weights) wi are assigned to vertices vi using rules of the form vi→wi.
Input rules should list vi→wi for all input vertices vi.
If input values are missing from rules, vertex names vi are assumed as values.
If rules includes a rule for an output vertex vi, the associated value is ignored and overwritten upon evaluation.
Function vfun accepts three arguments parallel over index i:
| #1 | a list of values wi on all vertices vi preceeding vj |
| #2 | a list of edge weights wij for each preceeding edge  |
| #3 | a list of all preceeding edges  |
If
vfun is specified as a symbol
sym (such as
Times or
Plus), then
vfun=sym@@#1&.
Optional specification of
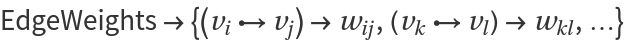
may simplify some calculations.
Values in
#2 are obtained most efficiently using an
Association, so it is possible to get a
Missing["KeyAbsent",_] error if the list of
EdgeWeights is incomplete.
Association expr has a primary key "Graph", which should point to a directed acyclic graph.
| "VertexWeights" | {} | a list of function values |
| "VertexFunction" | Plus | determines how to fold over incoming values |
| "EdgeWeights" | {} | weights or phases per graph edge |
The
Association expr is then effectively its own type of expression, which should have a definite evaluation.
Any expr that conforms to the schema outlined above should ultimately be easy to compile for optimized evaluation.
Ultimately,
ResourceFunction["DirectedAcyclicEvaluate"] returns a complete
Association listing all function values under key "VertexWeights".
The output
Association is certified in the sense that it is locally checkable on every graph vertex.
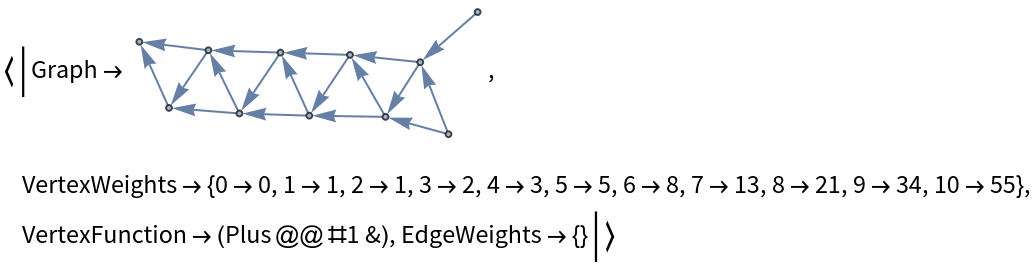
![fibonacci = ResourceFunction["DirectedAcyclicEvaluate"][
Graph[Flatten[
{DirectedEdge[#1, #3], DirectedEdge[#2, #3]
} & @@@ Partition[Range[0, #], 3, 1]],
GraphLayout -> "SpringEmbedding"]
] &[10]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/34c53e27f62a7ce8.png)
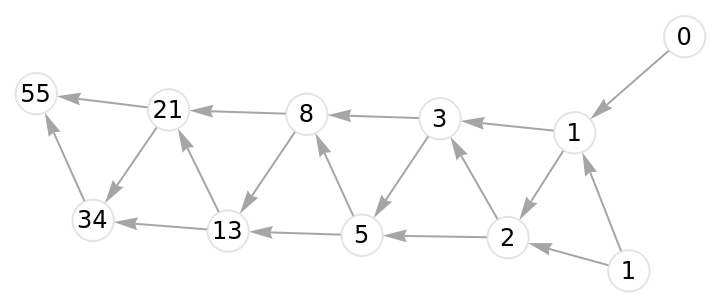
![Graph[fibonacci["Graph"], VertexLabels -> (#1 -> Placed[
Style[#2, 12], Center] & @@@ fibonacci["VertexWeights"]),
VertexStyle -> Directive[White, EdgeForm[LightGray]],
VertexSize -> 1/3, EdgeStyle -> Gray]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/7bc0b525fbc74f66.png)
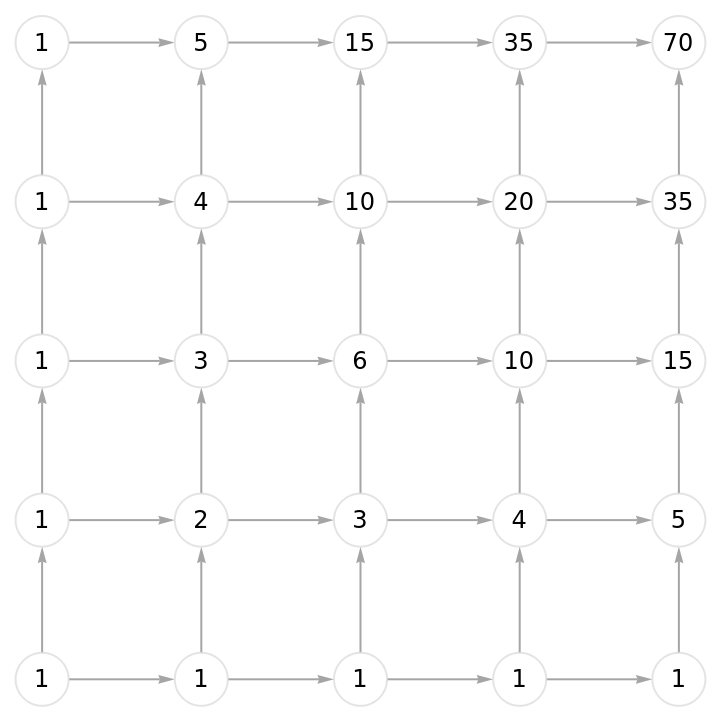
![With[{binomials = ResourceFunction["DirectedAcyclicEvaluate"][
Graph[GridGraph[{#, #},
DirectedEdges -> True]] &[5]]},
Graph[binomials["Graph"], VertexLabels -> (#1 -> Placed[
Style[#2, 12], Center] & @@@ binomials["VertexWeights"]),
VertexStyle -> Directive[White, EdgeForm[LightGray]],
VertexSize -> 1/3, EdgeStyle -> Gray]]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/2a5c31bb072184d7.png)
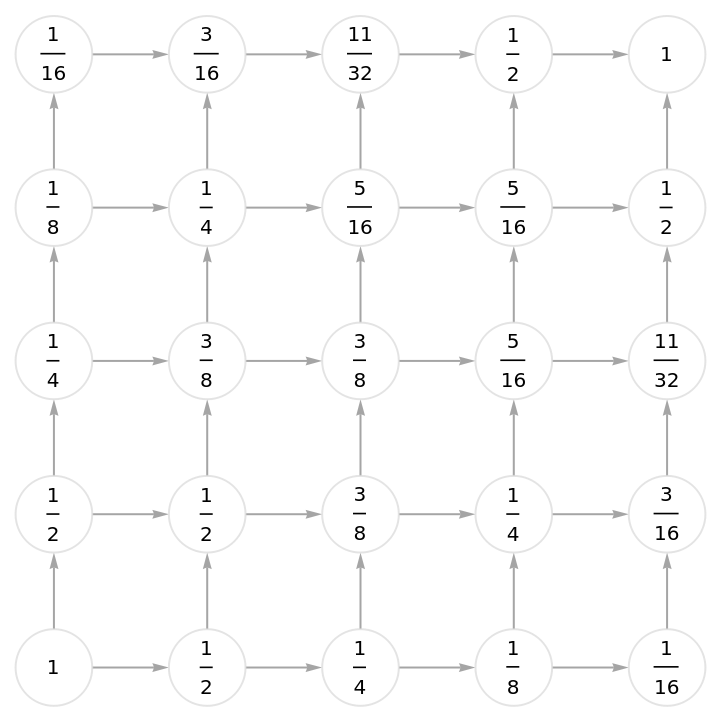
![Function[{graph0},
With[{binomials = ResourceFunction["DirectedAcyclicEvaluate"][
graph0, {_List :> 1}, Function[Total[#1*#2]],
"EdgeWeights" -> (# -> 1/VertexOutDegree[
graph0, #[[1]]] & /@ EdgeList[graph0])]},
Graph[binomials["Graph"], VertexLabels -> (#1 -> Placed[
Style[#2, 10], Center] & @@@ binomials["VertexWeights"]),
VertexStyle -> Directive[White, EdgeForm[LightGray]],
VertexSize -> 1/2, EdgeStyle -> Gray]]][
Graph[GridGraph[{5, 5}, DirectedEdges -> True]]]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/25ece80e6c660911.png)
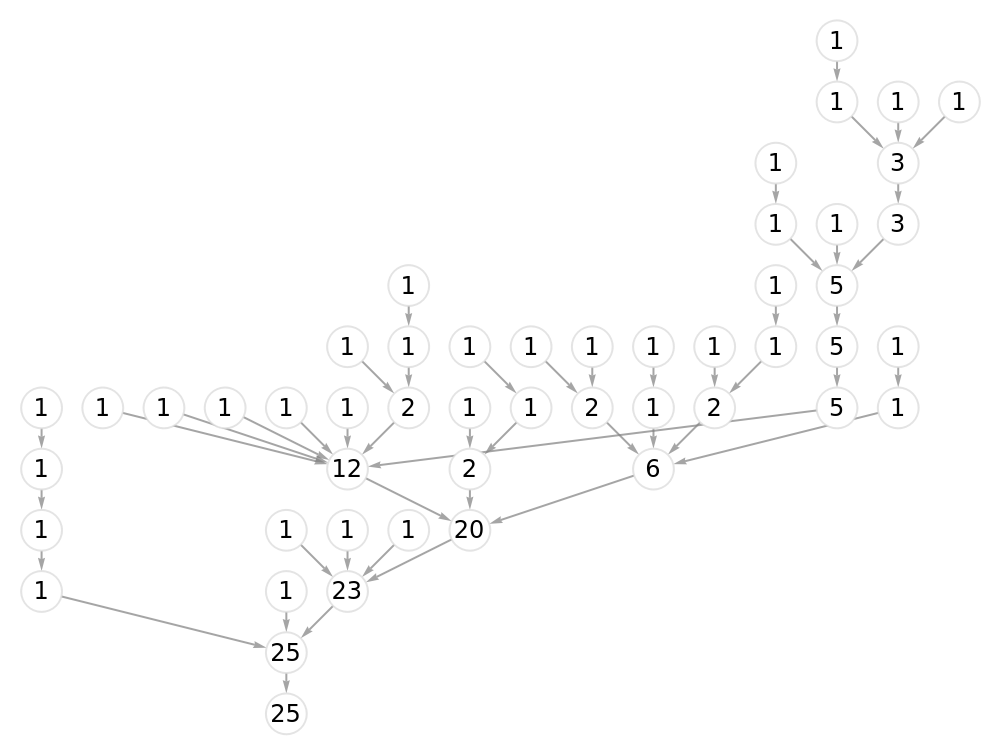
![With[{treeGraph0 = (SeedRandom["TreeTest"];
Graph[Reverse /@ EdgeList[TreeGraph[RandomTree[50]]]])},
Graph[#["Graph"], VertexLabels -> (#1 -> Placed[
Style[#2, 12], Center] & @@@ #["VertexWeights"]),
VertexStyle -> Directive[White, EdgeForm[LightGray]],
VertexSize -> 1/1.5, EdgeStyle -> Gray, ImageSize -> 500,
GraphLayout -> "LayeredDigraphEmbedding"] &@
ResourceFunction["DirectedAcyclicEvaluate"]@
Association["Graph" -> treeGraph0,
"VertexWeights" -> (# -> 1 & /@ Select[VertexList[treeGraph0],
SameQ[VertexInComponent[treeGraph0, #, {1}], {}] &])]]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/4ea212c5ce811f28.png)
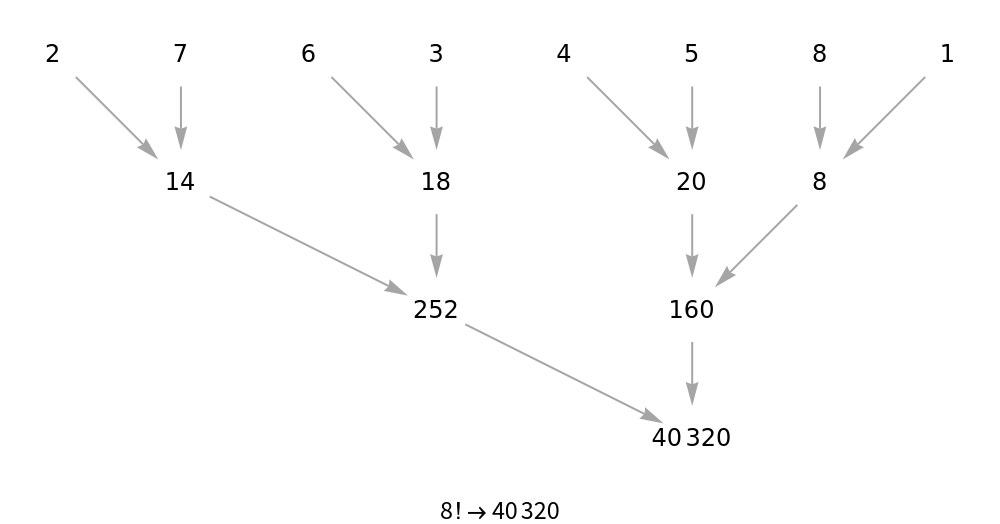
![With[{factorialEval = ResourceFunction["DirectedAcyclicEvaluate"][
Association["Graph" -> #,
"VertexWeights" -> {8 -> 2, 2 -> 8, 3 -> 5, 5 -> 3},
"VertexFunction" -> Times]]},
Labeled[Graph[factorialEval["Graph"], VertexLabels -> (#1 -> Placed[
Style[#2, 12], Center] & @@@ factorialEval["VertexWeights"]),
VertexStyle -> Directive[White, EdgeForm[None]],
VertexSize -> 1/2, EdgeStyle -> Gray, ImageSize -> 500],
Rule[HoldForm[8!], (2^4 - 1) /. factorialEval["VertexWeights"]]]
] &[VertexReplace[Graph[Reverse /@ EdgeList[
KaryTree[2^4 - 1, 2, DirectedEdges -> True]]],
{x_ :> 2^4 - x}]]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/12b412c9c7ae7d9f.png)
![With[{hypercubeEval = ResourceFunction["DirectedAcyclicEvaluate"][Association[
"Graph" -> GridGraph[{2, 2, 2, 2}, DirectedEdges -> True],
"VertexFunction" -> Function[{values, edgeWeights, edges},
Fold[Vee, LongRightArrow @@@ Transpose[{values, edges[[All, 2]]}]]]
]]}, Grid[{{Graph[hypercubeEval["Graph"]]},
{16 /. hypercubeEval["VertexWeights"]}},
ItemSize -> 40]]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/51a5d3780e1217db.png)

![With[{hypercubeEval = ResourceFunction["DirectedAcyclicEvaluate"][Association[
"Graph" -> GridGraph[{2, 2, 2, 2}, DirectedEdges -> True],
"VertexFunction" -> Function[{values, edgeWeights, edges},
Fold[If[OddQ[edges[[1, 2]]], Vee, Wedge], If[OddQ[#2],
UpperRightArrow[#1, #3], LowerRightArrow[#1, #3]
] & @@@ Transpose[{values, edges[[All, 1]], edges[[All, 2]]}]]]
]]}, Grid[{{Graph[hypercubeEval["Graph"]]},
{16 /. hypercubeEval["VertexWeights"]}},
ItemSize -> 40]]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/63a00402b9ca2f6b.png)

![CertifyDAGEvaluate[function_Association] := With[{ioMaps = DeleteCases[{
VertexInComponent[function["Graph"], #, {1}],
#} & /@ VertexList[function["Graph"]], {{}, _}]},
Function[{ins, out}, Subtract[out /. function["VertexWeights"],
Apply[function["VertexFunction"], Transpose[
{# /. function["VertexWeights"],
DirectedEdge[#, out] /. function["EdgeWeights"],
DirectedEdge[#, out]} & /@ ins]]]] @@@ ioMaps]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/132d25f312d857bc.png)
![With[{A318495 = ResourceFunction["DirectedAcyclicEvaluate"][Graph[Flatten[
{DirectedEdge[#1, #3], DirectedEdge[#2, #3]
} & @@@ Partition[Range[0, #], 3, 1]],
GraphLayout -> "SpringEmbedding"],
{0 -> 1, 1 -> 10}, (Apply[Plus, #1*(#3 /. {
DirectedEdge[x_, y_] :> If[y - x == 1,
(59 y^2 - 59 y + 20)/2/y^2,
-6 (6 y - 7) (6 y - 5)/y^2]})] &)] &[10]},
Append[A318495, "ValuesCertificate" -> CertifyDAGEvaluate[A318495]]]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/5008328ebbd7d3ee.png)

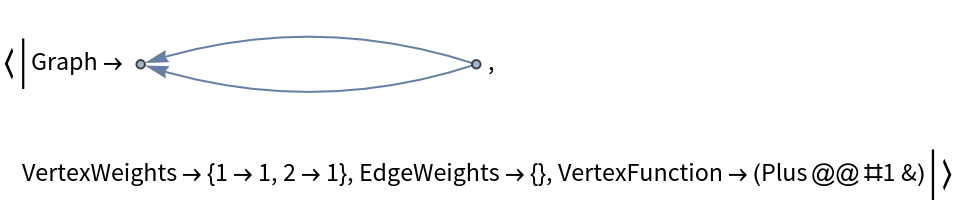
![ResourceFunction["DirectedAcyclicEvaluate"][Association[
"Graph" -> Graph[{DirectedEdge[1, 2]}],
"EdgeWeights" -> {DirectedEdge[1, 2] -> 2},
"VertexFunction" -> (Apply[Plus, #1*#2] &)]]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/4b9f2e815e63f039.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/18867e1d-4a68-43c2-872f-84a23065eb1a"]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/158c5aa532c3adfc.png)
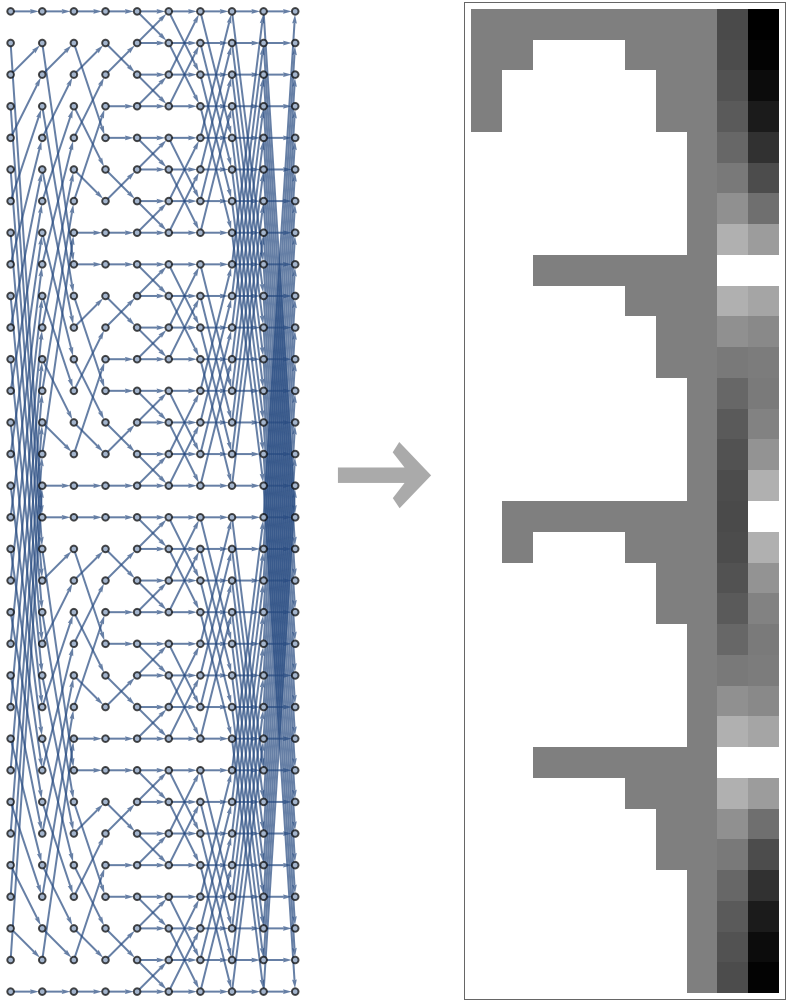
![Function[{dim}, With[{
fubiniEval = ResourceFunction["DirectedAcyclicEvaluate"][Association[
"Graph" -> Graph[Flatten[If[
And[SubsetQ[#1, #2], ! SameQ[#1, #2]]
, DirectedEdge[#2, #1], {} ] & @@@ Tuples[
Subsets[Range[dim]], {2}]]],
"VertexWeights" -> {{} -> 1}]]},
Graph[fubiniEval["Graph"], VertexLabels -> (
#1 -> Style[#2, 16] & @@@ Map[First,
GatherBy[fubiniEval["VertexWeights"],
{#[[2]], Length[#[[1]]]} &]]),
EdgeStyle -> LightGray, AspectRatio -> 2/3]]][5]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/7cce2ab7b84ffc17.png)

![Grid[MapThread[Function[{label, fun},
Prepend[
Times @@ fun[#] /. ResourceFunction["DirectedAcyclicEvaluate"][
GridGraph[fun[#], DirectedEdges -> True]
]["VertexWeights"] & /@ Range[1, 5], label]
], {TraditionalForm /@ {s == 3, s == 4, s == 6},
{Function[{#, #, #}],
Function[{#, #, 2 # - 1}],
Function[{#, 2 # - 1, 3 # - 2}]}}],
Frame -> All, Spacings -> {2, 1}, FrameStyle -> LightGray]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/12f27bb2461a44c0.png)

![Grid[MapThread[Function[{label, fun},
Prepend[CoefficientList[Normal@Series[fun, {z, 0, 4}], z],
label]], {TraditionalForm /@ {s == 3, s == 4, s == 6},
MapThread[Hypergeometric2F1[1/#1, 1 - 1/#1, 1, #2 z] &,
{{3, 4, 6}, {3^3, 4^3, 2 6^3}}]}],
Frame -> All, Spacings -> {2, 1}, FrameStyle -> LightGray]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/513c71ab5abe2008.png)

![With[{SierpinskiGraph = Graph[
ReplaceAll[EdgeList[NearestNeighborGraph[Position[
Function[{n}, Nest[ArrayFlatten[
{{#, #, #}, {#, 0, #}, {#, #, #}}
] &, 1, n]][2], 1]]],
UndirectedEdge[x_, y_] :> If[Total[y - x] > 0,
DirectedEdge[x, y], DirectedEdge[y, x]]]]},
ResourceFunction["DirectedAcyclicEvaluate"][
SierpinskiGraph, {{1, 1} -> 1}]]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/66bacec230b91d24.png)
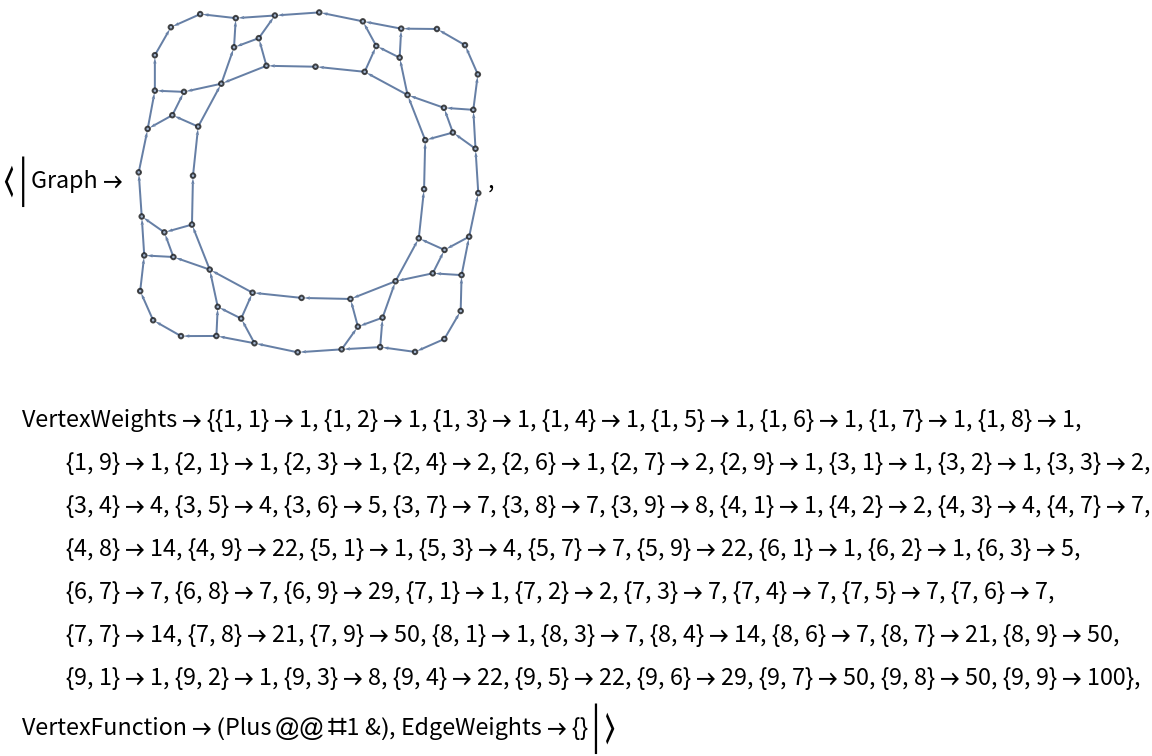
![Function[{dim}, With[{SierpinskiGraph = Graph[
ReplaceAll[EdgeList[NearestNeighborGraph[Position[
Function[{n}, Nest[ArrayFlatten[
{{#, #, #}, {#, 0, #}, {#, #, #}}
] &, 1, n]][dim], 1]]],
UndirectedEdge[x_, y_] :> If[Total[y - x] > 0,
DirectedEdge[x, y], DirectedEdge[y, x]]]]},
{3^dim, 3^dim} /. ResourceFunction["DirectedAcyclicEvaluate"][
SierpinskiGraph, {{1, 1} -> 1}]["VertexWeights"]]] /@ Range[4]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/6319c36c7c89ea0d.png)
![Function[{dim}, With[{MengerGraph = Graph[
ReplaceAll[EdgeList[NearestNeighborGraph[Position[
Function[{n}, With[{face = Nest[ArrayFlatten[
{{#, #, #}, {#, 0, #}, {#, #, #}}] &, 1, n]}, Outer[Times[face[[#1, #2]], face[[#2, #3]] , face[[#3, #1]] ] &,
Range[Length[face]],
Range[Length[face]],
Range[Length[face]], 1]]][dim], 1]]],
UndirectedEdge[x_, y_] :> If[Total[y - x] > 0,
DirectedEdge[x, y], DirectedEdge[y, x]]]]},
{3^dim, 3^dim, 3^dim} /. ResourceFunction["DirectedAcyclicEvaluate"][
MengerGraph, {{1, 1, 1} -> 1}]["VertexWeights"]]] /@ Range[3]](https://www.wolframcloud.com/obj/resourcesystem/images/6a9/6a982fd7-4993-4495-aced-a4d53a852dbc/1-1-0/5f092ef11451c97c.png)