Function Repository Resource:

DirectedAcyclicEvaluate

Evaluate functions locally over any directed acyclic graph

Contributed by: Bradley Klee

ResourceFunction["DirectedAcyclicEvaluate"][graph,rules]

assigns values to the vertices of a directed acyclic graph by recursively summing over preceding values, starting from initial values listed in rules.

ResourceFunction["DirectedAcyclicEvaluate"][graph,rules,vfun]

allows for a wide range of calculations via specified function vfun, which evaluates locally on each vertex (see Details).

ResourceFunction["DirectedAcyclicEvaluate"][expr]

allows specification of expr as an Association with the keys "Graph", "VertexWeights", "VertexFunction", and optionally "EdgeWeights".

Details

Graph vertices can be thought of as named memory locations for both inputs and outputs.

Evaluation distinguishes inputs as the set of root vertices not pointed to by any directed edge (sources).

All other vertices reached by following directed edges are considered outputs.

A vertex v_i and its edge

are both said to precede another vertex v_j, if the graph indeed contains edge

Values (or weights) w_i are assigned to vertices v_i using rules of the form v_i→w_i.

Input rules should list v_i→w_i for all input vertices v_i.

If input values are missing from rules, vertex names v_i are assumed as values.

If rules includes a rule for an output vertex v_i, the associated value is ignored and overwritten upon evaluation.

Function vfun accepts three arguments parallel over index i:

a list of values w_i on all vertices v_i preceeding v_j

a list of edge weights w_ij for each preceeding edge

a list of all preceeding edges

If vfun is specified as a symbol sym (such as Times or Plus), then vfun=sym@@#1&.

Optional specification of

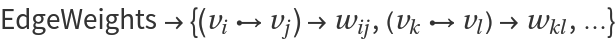
may simplify some calculations.

Values in #2 are obtained most efficiently using an Association, so it is possible to get a Missing["KeyAbsent",_] error if the list of EdgeWeights is incomplete.

ResourceFunction["DirectedAcyclicEvaluate"] also acts as Evaluate on an Unevaluated expr, which is formatted as an Association.

Association expr has a primary key "Graph", which should point to a directed acyclic graph.

Optional Keys of the Association and their default values are:

"VertexWeights"

{}

a list of function values

"VertexFunction"

Plus

determines how to fold over incoming values

"EdgeWeights"

{}

weights or phases per graph edge

The Association expr is then effectively its own type of expression, which should have a definite evaluation.

Any expr that conforms to the schema outlined above should ultimately be easy to compile for optimized evaluation.

Ultimately, ResourceFunction["DirectedAcyclicEvaluate"] returns a complete Association listing all function values under key "VertexWeights".

The output Association is certified in the sense that it is locally checkable on every graph vertex.

Examples

Basic Examples (3)

Enumerate the first few terms of the Fibonacci sequence:

In[1]:=

fibonacci = ResourceFunction[
"DirectedAcyclicEvaluate", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][
Graph[Flatten[
{DirectedEdge[#1, #3], DirectedEdge[#2, #3]
} & @@@ Partition[Range[0, #], 3, 1]],
GraphLayout -> "SpringEmbedding"]
] &[10]

Out[1]=

Compare with pre-compiled function Fibonacci:

In[2]:=

Out[2]=

Depict the Fibonacci calculation on its directed graph:

In[3]:=

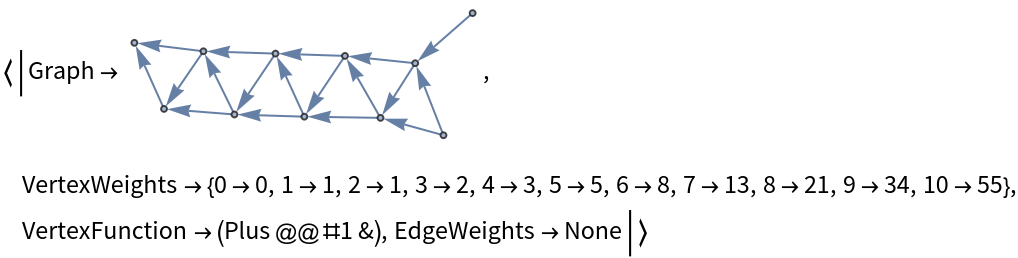
Graph[fibonacci["Graph"], VertexLabels -> (#1 -> Placed[
Style[#2, 12], Center] & @@@ fibonacci["VertexWeights"]),
VertexStyle -> Directive[White, EdgeForm[LightGray]],
VertexSize -> 1/3, EdgeStyle -> Gray]

Out[3]=

Scope (5)

Count walks on a directed grid:

In[4]:=

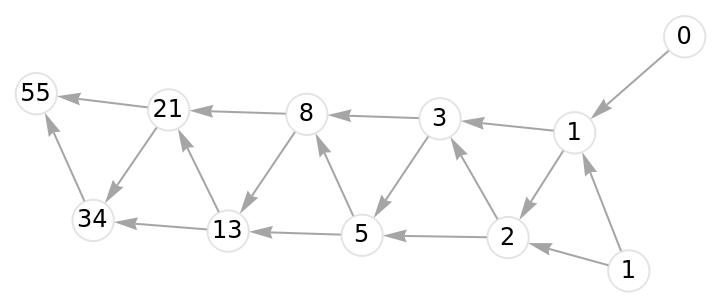
With[{binomials = ResourceFunction[
"DirectedAcyclicEvaluate", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][
Graph[GridGraph[{#, #},
DirectedEdges -> True]] &[5]]},
Graph[binomials["Graph"], VertexLabels -> (#1 -> Placed[
Style[#2, 12], Center] & @@@ binomials["VertexWeights"]),
VertexStyle -> Directive[White, EdgeForm[LightGray]],
VertexSize -> 1/3, EdgeStyle -> Gray]]

Out[4]=

Convert to partial probabilities by adding edge weights:

In[5]:=

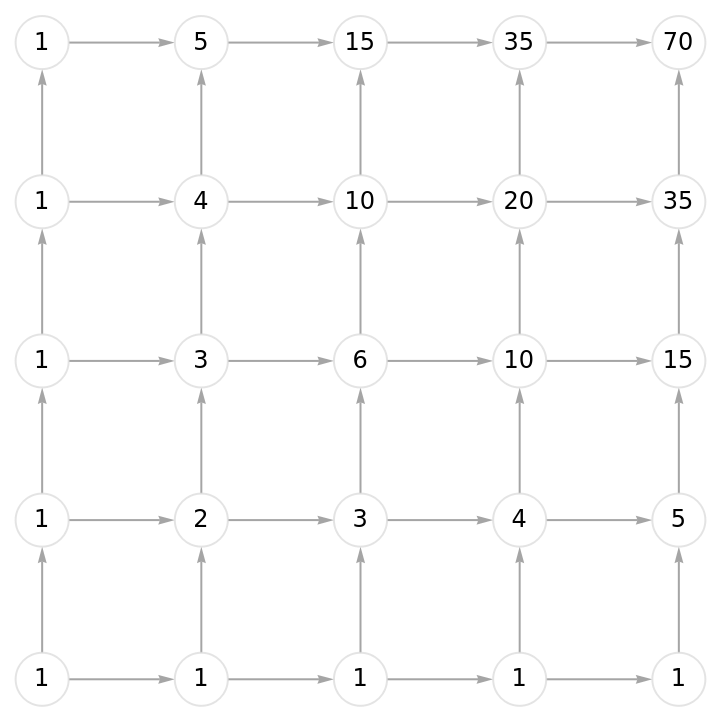
$Function[{graph0}, With[{binomials = ResourceFunction[ "DirectedAcyclicEvaluate", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ graph0, {_List :> 1}, Function[Total[#1*#2]], "EdgeWeights" -> (# -> 1/VertexOutDegree[ graph0, #[[1]]] & /@ EdgeList[graph0])]}, Graph[binomials["Graph"], VertexLabels -> (#1 -> Placed[ Style[#2, 10], Center] & @@@ binomials["VertexWeights"]), VertexStyle -> Directive[White, EdgeForm[LightGray]], VertexSize -> 1/2, EdgeStyle -> Gray]]][ Graph[GridGraph[{5, 5}, DirectedEdges -> True]]]$

Out[5]=

Count the leaves on a random tree:

In[6]:=

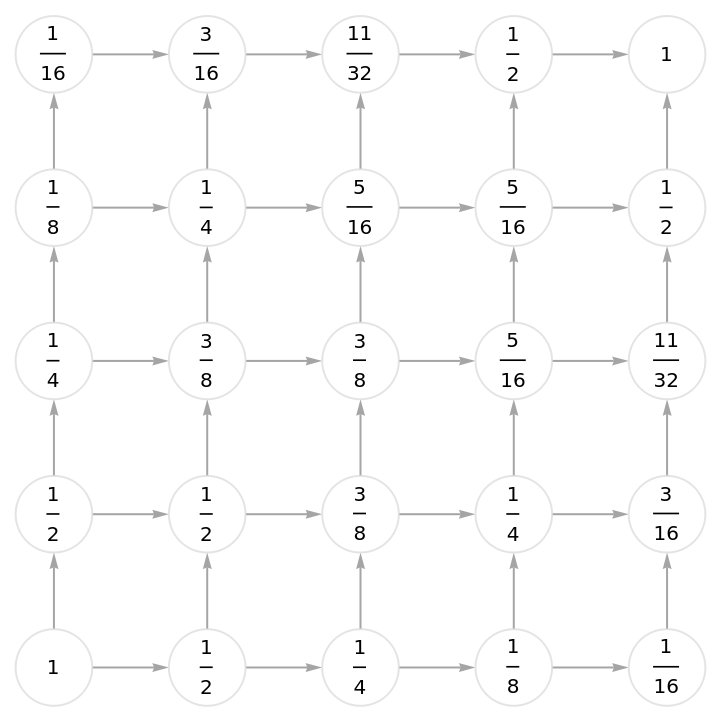
With[{treeGraph0 = (SeedRandom["TreeTest"];
Graph[Reverse /@ EdgeList[TreeGraph[RandomTree[50]]]])},
Graph[#["Graph"], VertexLabels -> (#1 -> Placed[
Style[#2, 12], Center] & @@@ #["VertexWeights"]),
VertexStyle -> Directive[White, EdgeForm[LightGray]],
VertexSize -> 1/1.5, EdgeStyle -> Gray, ImageSize -> 500,
GraphLayout -> "LayeredDigraphEmbedding"] &@
ResourceFunction[
"DirectedAcyclicEvaluate", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"]@Association["Graph" -> treeGraph0,
"VertexWeights" -> (# -> 1 & /@ Select[VertexList[treeGraph0],
SameQ[VertexInComponent[treeGraph0, #, {1}], {}] &])]]

Out[6]=

Evaluate a Factorial number using binary splitting:

In[7]:=

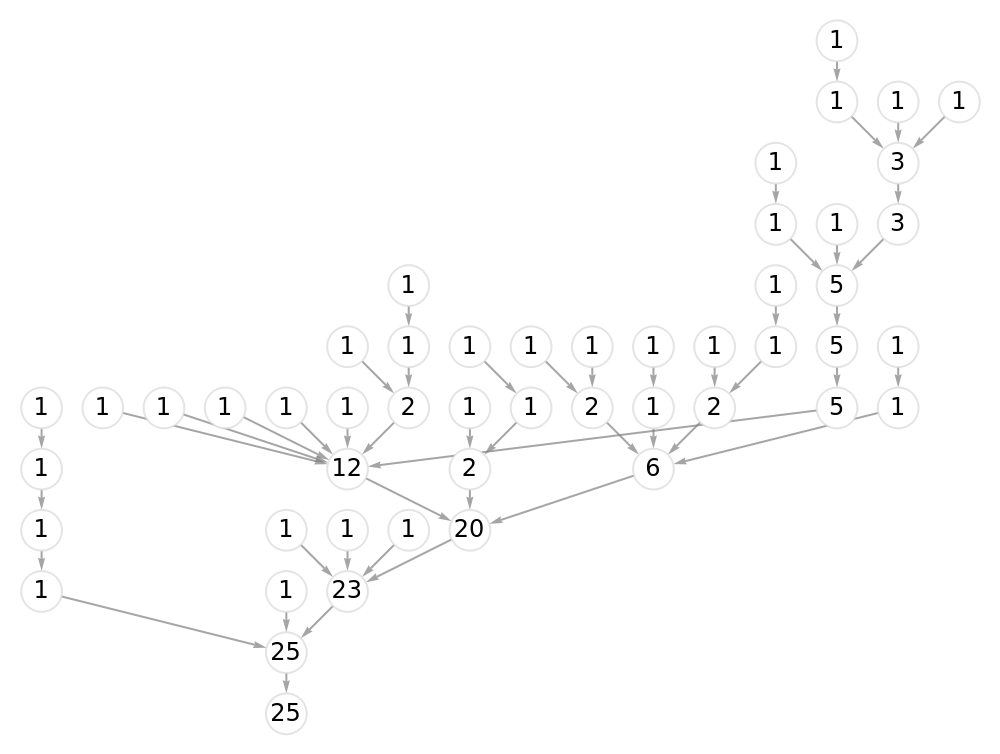
$With[{factorialEval = ResourceFunction[ "DirectedAcyclicEvaluate", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ Association["Graph" -> #, "VertexWeights" -> {8 -> 2, 2 -> 8, 3 -> 5, 5 -> 3}, "VertexFunction" -> Times]]}, Labeled[Graph[factorialEval["Graph"], VertexLabels -> (#1 -> Placed[ Style[#2, 12], Center] & @@@ factorialEval["VertexWeights"]), VertexStyle -> Directive[White, EdgeForm[None]], VertexSize -> 1/2, EdgeStyle -> Gray, ImageSize -> 500], Rule[HoldForm[8!], (2^4 - 1) /. factorialEval["VertexWeights"]]] ] &[VertexReplace[Graph[Reverse /@ EdgeList[ KaryTree[2^4 - 1, 2, DirectedEdges -> True]]], {x_ :> 2^4 - x}]]$

Out[7]=

Use symbolic functions to create an encoding of 24 branching and merging traversals of a hypercube:

In[8]:=

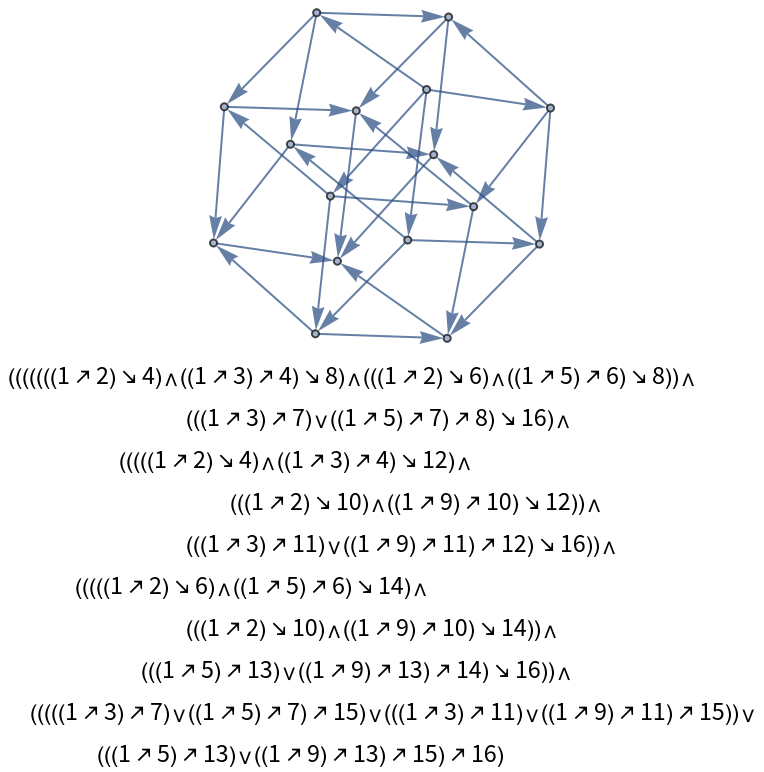
With[{hypercubeEval = ResourceFunction[
"DirectedAcyclicEvaluate", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][Association[
"Graph" -> GridGraph[{2, 2, 2, 2}, DirectedEdges -> True],
"VertexFunction" -> Function[{values, edgeWeights, edges},
Fold[Vee, LongRightArrow @@@ Transpose[{values, edges[[All, 2]]}]]]
]]}, Grid[{{Graph[hypercubeEval["Graph"]]},
{16 /. hypercubeEval["VertexWeights"]}},
ItemSize -> 40]]

Out[8]=

Split path symbols based on parity of the outgoing and incoming vertices:

In[9]:=

Out[9]=

Properties and Relations (2)

Valid output Association instances should cause the following check function to list zeros:

In[10]:=

$CertifyDAGEvaluate[function_Association] := With[{ioMaps = DeleteCases[{ VertexInComponent[function["Graph"], #, {1}], #} & /@ VertexList[function["Graph"]], {{}, _}]}, Function[{ins, out}, Subtract[out /. function["VertexWeights"], Apply[function["VertexFunction"], Transpose[ {# /. function["VertexWeights"], DirectedEdge[#, out] /. If[function["EdgeWeights"] == None, {}, function["EdgeWeights"]], DirectedEdge[#, out]} & /@ ins]]]] @@@ ioMaps]$

Double check a p-recurrence important to the theory of algebraic sphere curves (cf. OEIS A318495):

In[11]:=

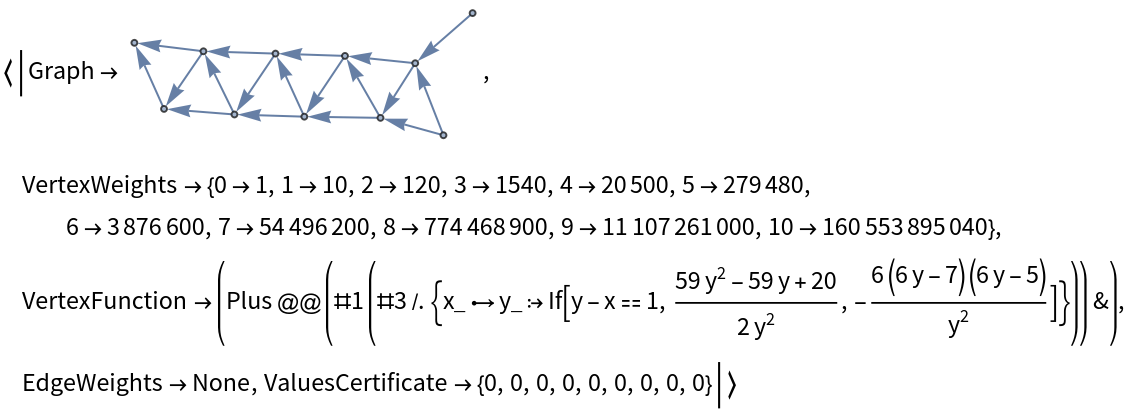
$With[{A318495 = ResourceFunction[ "DirectedAcyclicEvaluate", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][Graph[Flatten[ {DirectedEdge[#1, #3], DirectedEdge[#2, #3] } & @@@ Partition[Range[0, #], 3, 1]], GraphLayout -> "SpringEmbedding"], {0 -> 1, 1 -> 10}, (Apply[Plus, #1*(#3 /. { DirectedEdge[x_, y_] :> If[y - x == 1, (59 y^2 - 59 y + 20)/2/y^2, -6 (6 y - 7) (6 y - 5)/y^2]})] &)] &[10]}, Append[A318495, "ValuesCertificate" -> CertifyDAGEvaluate[A318495]]]$

Out[11]=

Possible Issues (3)

Invalid inputs result in a failure message:

In[12]:=

Out[12]=

In[13]:=

Out[13]=

DirectedAcyclicEvaluate ignores double edges:

In[14]:=

Out[14]=

If necessary, a corrected input could assign a factor of 2 via EdgeWeights:

In[15]:=

ResourceFunction[
"DirectedAcyclicEvaluate", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][Association[
"Graph" -> Graph[{DirectedEdge[1, 2]}],
"EdgeWeights" -> {DirectedEdge[1, 2] -> 2},
"VertexFunction" -> (Apply[Plus, #1*#2] &)]]

Out[15]=

Neat Examples (4)

Calculate a Fourier transform with only n Log₂ n complexity (n=32):

In[16]:=

(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/bd53a0ae-1fe0-48b9-b691-3ff6282ebaab"]

Out[16]=

Calculate the first few Fubini numbers (OEIS A000670):

In[17]:=

Function[{dim}, With[{
fubiniEval = ResourceFunction[
"DirectedAcyclicEvaluate", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][Association[
"Graph" -> Graph[Flatten[If[
And[SubsetQ[#1, #2], ! SameQ[#1, #2]]
, DirectedEdge[#2, #1], {} ] & @@@ Tuples[
Subsets[Range[dim]], {2}]]],
"VertexWeights" -> {{} -> 1}]]},
Graph[fubiniEval["Graph"], VertexLabels -> (
#1 -> Style[#2, 16] & @@@ Map[First,
GatherBy[fubiniEval["VertexWeights"],
{#[[2]], Length[#[[1]]]} &]]),
EdgeStyle -> LightGray, AspectRatio -> 2/3]]][5]

Out[17]=

Count corner-to-corner walks on three-dimensional grids:

In[18]:=

Grid[MapThread[Function[{label, fun},
Prepend[
Times @@ fun[#] /. ResourceFunction[
"DirectedAcyclicEvaluate", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][
GridGraph[fun[#], DirectedEdges -> True]
]["VertexWeights"] & /@ Range[1, 5], label]
], {TraditionalForm /@ {s == 3, s == 4, s == 6},
{Function[{#, #, #}],
Function[{#, #, 2 # - 1}],
Function[{#, 2 # - 1, 3 # - 2}]}}],
Frame -> All, Spacings -> {2, 1}, FrameStyle -> LightGray]

Out[18]=

Compare with series expansion of Ramanujan's elliptic integrals:

In[19]:=

$Grid[MapThread[Function[{label, fun}, Prepend[CoefficientList[Normal@Series[fun, {z, 0, 4}], z], label]], {TraditionalForm /@ {s == 3, s == 4, s == 6}, MapThread[Hypergeometric2F1[1/#1, 1 - 1/#1, 1, #2 z] &, {{3, 4, 6}, {3^3, 4^3, 2 6^3}}]}], Frame -> All, Spacings -> {2, 1}, FrameStyle -> LightGray]$

Out[19]=

Count corner-to-corner walks on the cells of MengerMesh when n=2:

In[20]:=

$With[{SierpinskiGraph = Graph[ ReplaceAll[EdgeList[NearestNeighborGraph[Position[ Function[{n}, Nest[ArrayFlatten[ {{#, #, #}, {#, 0, #}, {#, #, #}} ] &, 1, n]][2], 1]]], UndirectedEdge[x_, y_] :> If[Total[y - x] > 0, DirectedEdge[x, y], DirectedEdge[y, x]]]]}, ResourceFunction[ "DirectedAcyclicEvaluate", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][SierpinskiGraph, {{1, 1} -> 1}]]$

Out[20]=

Repeat this calculation for sequential inputs, then output maximum path counts:

In[21]:=

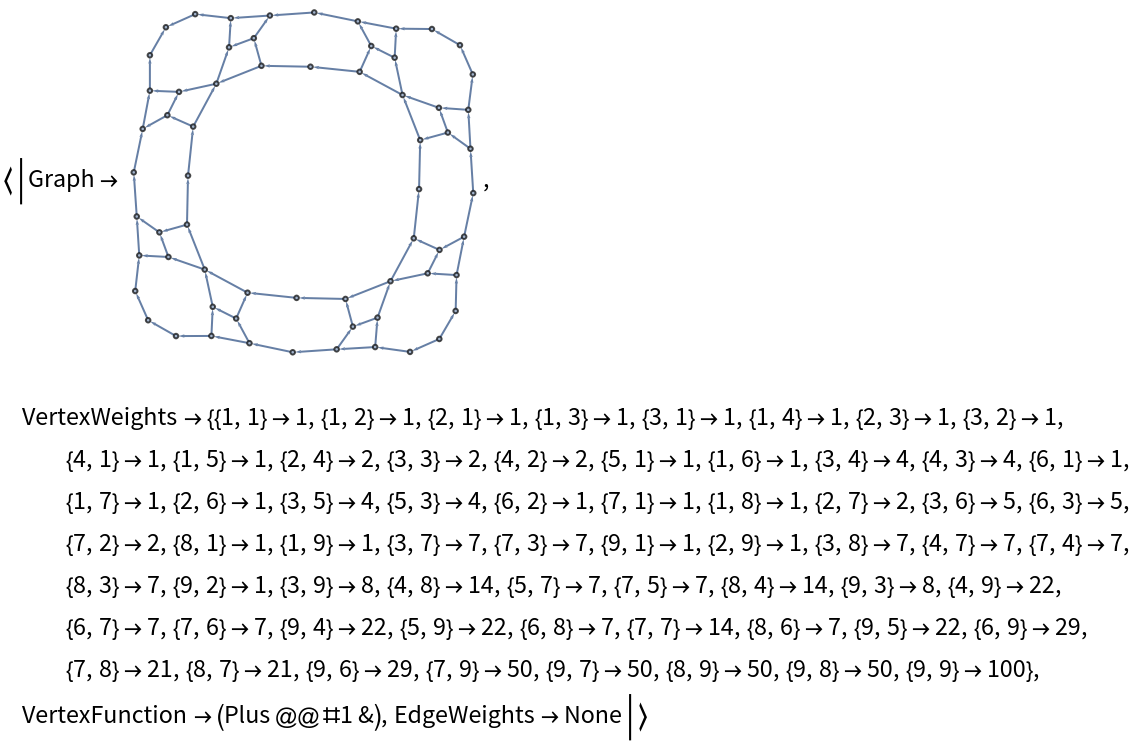
$Function[{dim}, With[{SierpinskiGraph = Graph[ ReplaceAll[EdgeList[NearestNeighborGraph[Position[ Function[{n}, Nest[ArrayFlatten[ {{#, #, #}, {#, 0, #}, {#, #, #}} ] &, 1, n]][dim], 1]]], UndirectedEdge[x_, y_] :> If[Total[y - x] > 0, DirectedEdge[x, y], DirectedEdge[y, x]]]]}, {3^dim, 3^dim} /. ResourceFunction[ "DirectedAcyclicEvaluate", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ SierpinskiGraph, {{1, 1} -> 1}]["VertexWeights"]]] /@ Range[4]$

Out[21]=

Try a similar calculation for the Menger sponge (a.k.a. MengerMesh with d=3):

In[22]:=

$Function[{dim}, With[{MengerGraph = Graph[ ReplaceAll[EdgeList[NearestNeighborGraph[Position[ Function[{n}, With[{face = Nest[ArrayFlatten[ {{#, #, #}, {#, 0, #}, {#, #, #}}] &, 1, n]}, Outer[Times[face[[#1, #2]], face[[#2, #3]] , face[[#3, #1]] ] &, Range[Length[face]], Range[Length[face]], Range[Length[face]], 1]]][dim], 1]]], UndirectedEdge[x_, y_] :> If[Total[y - x] > 0, DirectedEdge[x, y], DirectedEdge[y, x]]]]}, {3^dim, 3^dim, 3^dim} /. ResourceFunction[ "DirectedAcyclicEvaluate", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ MengerGraph, {{1, 1, 1} -> 1}]["VertexWeights"]]] /@ Range[3]$