Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Display a dashed tube in 3D graphics
ResourceFunction["DashedTube"][{{x1,y1,z1},{x2,y2,z2},…}] represents a 3D dashed tube around the line joining a sequence of points. | |
ResourceFunction["DashedTube"][{pt1,pt2,…},r] represents a dashed tube of radius r. | |
ResourceFunction["DashedTube"][{pt1,pt2,…},r,dash] specifies a dashing dash of a tube. | |
ResourceFunction["DashedTube"][{pt1,pt2,…},{r1,r2,…}] specifies a different tube radius at the position of each of the points pti. | |
ResourceFunction["DashedTube"][{{pt11,pt12,…},{pt21,…},…},…] represents a collection of dashed tubes. | |
ResourceFunction["DashedTube"][curve,…] represents a dashed tube around the specified 3D curve. |
| Line[…] | piecewise line segments |
| BezierCurve[…] | composite Bezier curve |
| BSplineCurve[…] | B-spline curve |
| VertexColors | Automatic | vertex colors to be interpolated |
| "Each" | False | whether to apply styling to each dashed segment separately |
| PlotPoints | 30 | initial number of sampling points of the input curve |
| MaxIterations | 20 | maximum number of subdivisions during the sampling |
Create a simple dashed tube:
| In[1]:= |
| Out[1]= | 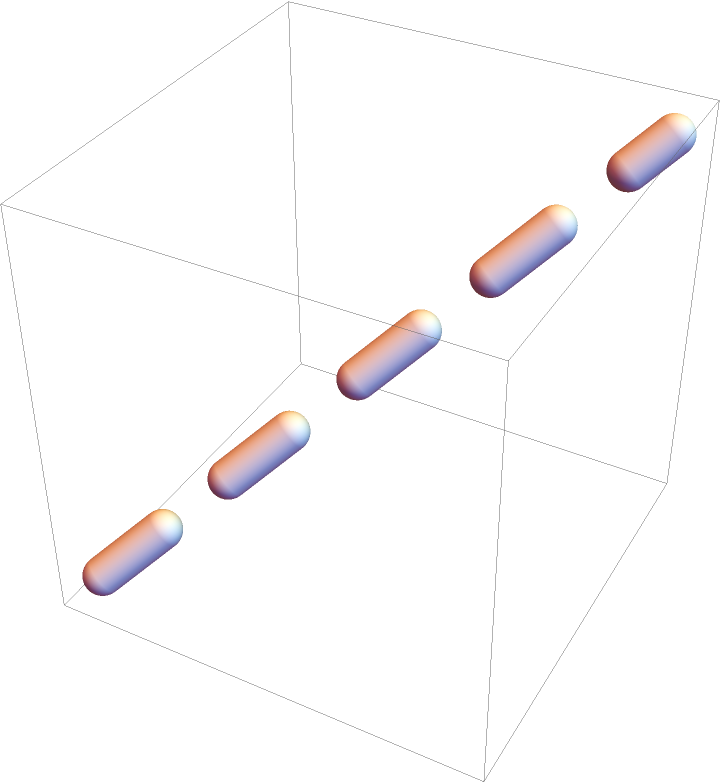 |
A dashed tube along a curve:
| In[2]:= |
| Out[2]= | 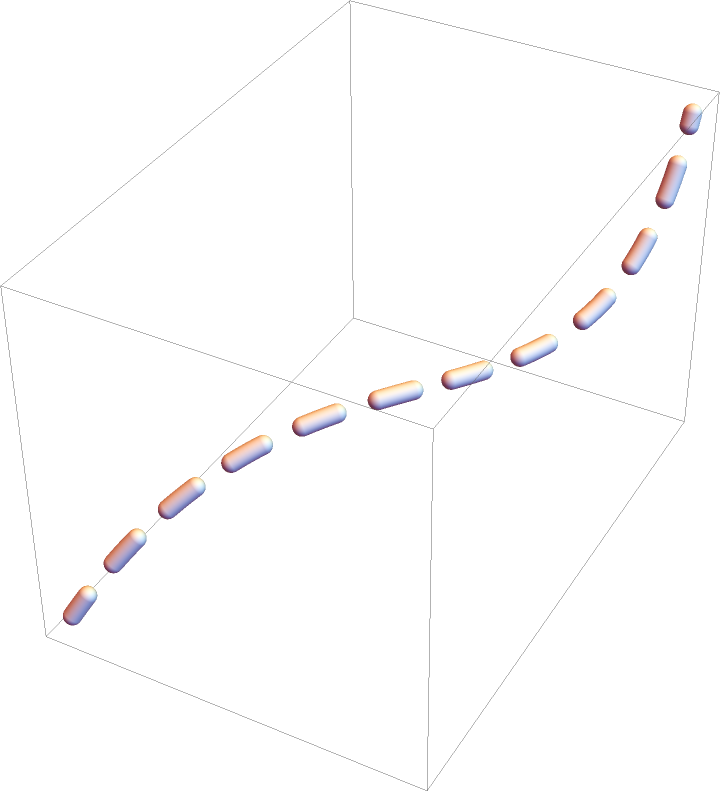 |
A dashed tube with radius 0.1:
| In[3]:= |
| Out[3]= | 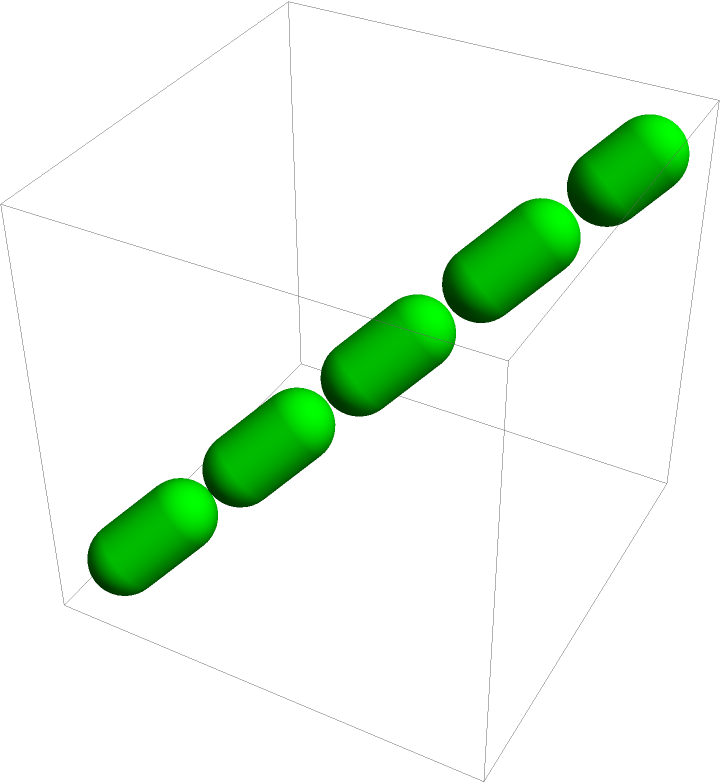 |
A dashed tube with dashing {0.2,0.05}:
| In[4]:= |
| Out[4]= | 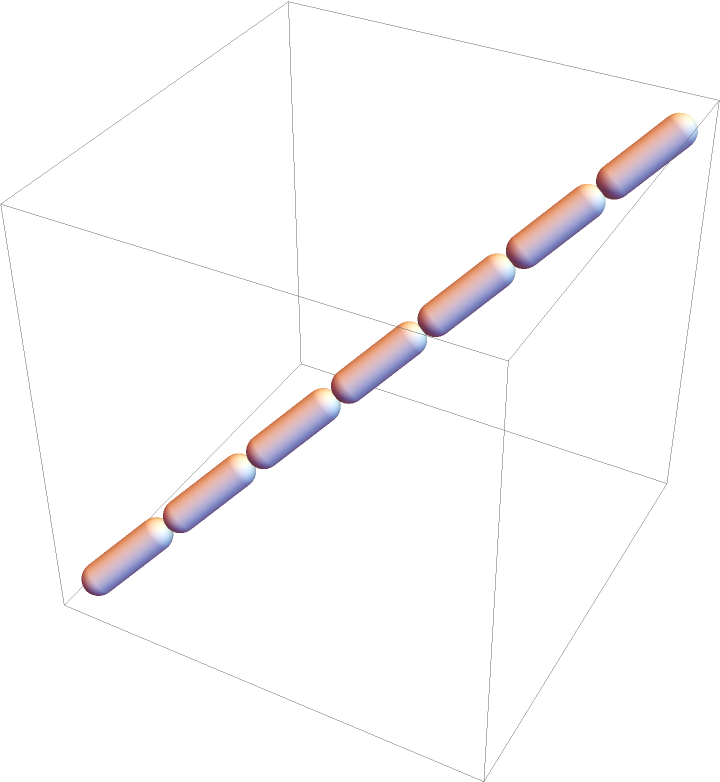 |
Add an Arrow:
| In[5]:= |
| Out[5]= | 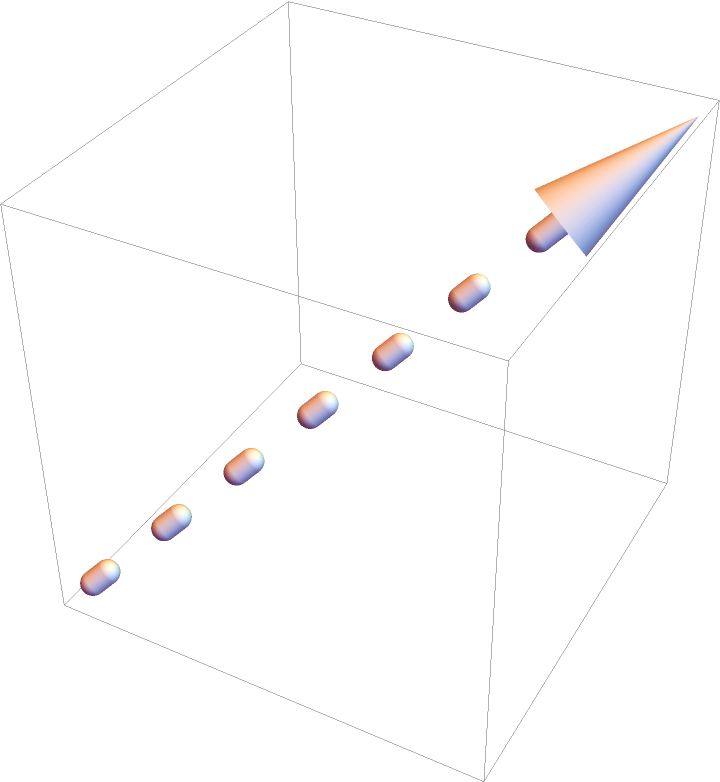 |
Differently styled dashed tubes:
| In[6]:= |
| In[7]:= |
| Out[7]= | 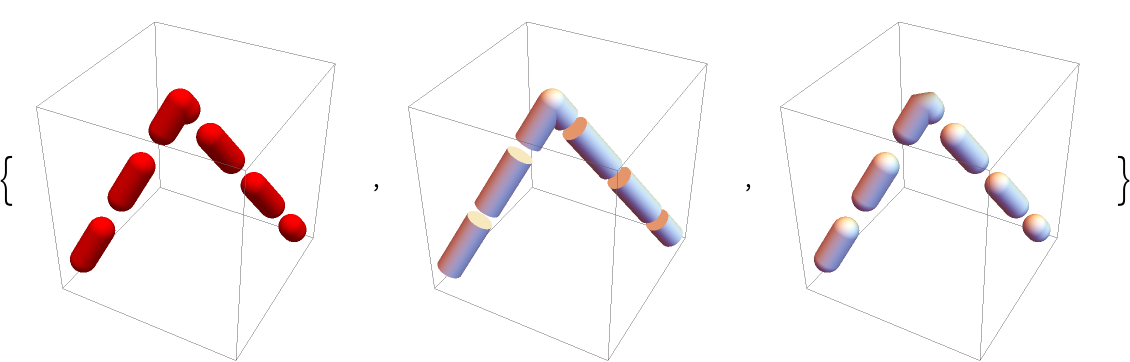 |
Gradient coloring:
| In[8]:= |
| In[9]:= |
| Out[9]= | 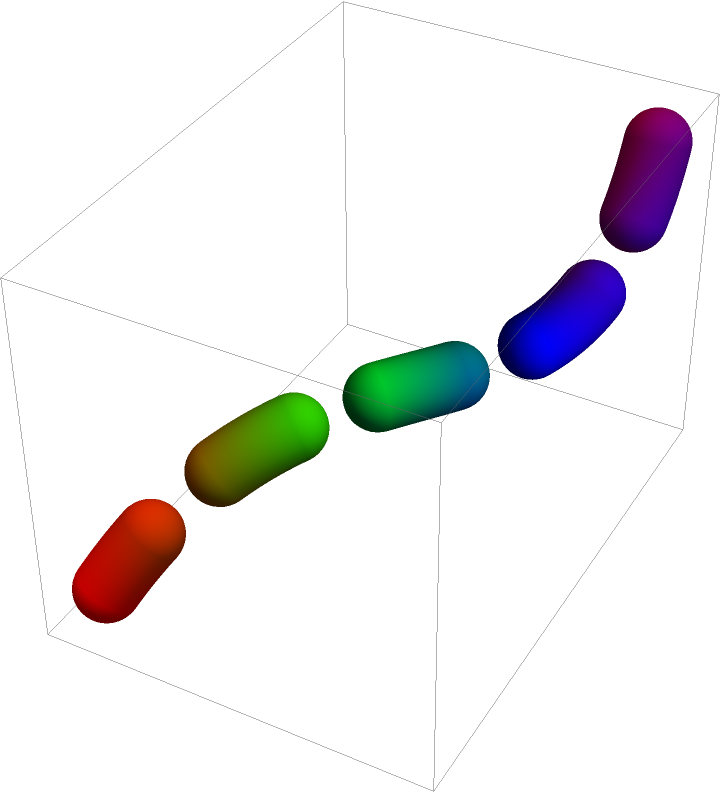 |
Gradient coloring for each segment independently:
| In[10]:= |
| In[11]:= | ![Graphics3D[
ResourceFunction["DashedTube"][curve, 0.2, 0.5, VertexColors -> {Red, Green, Blue, Purple}, "Each" -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/504dadfa4e347cd4.png) |
| Out[11]= | 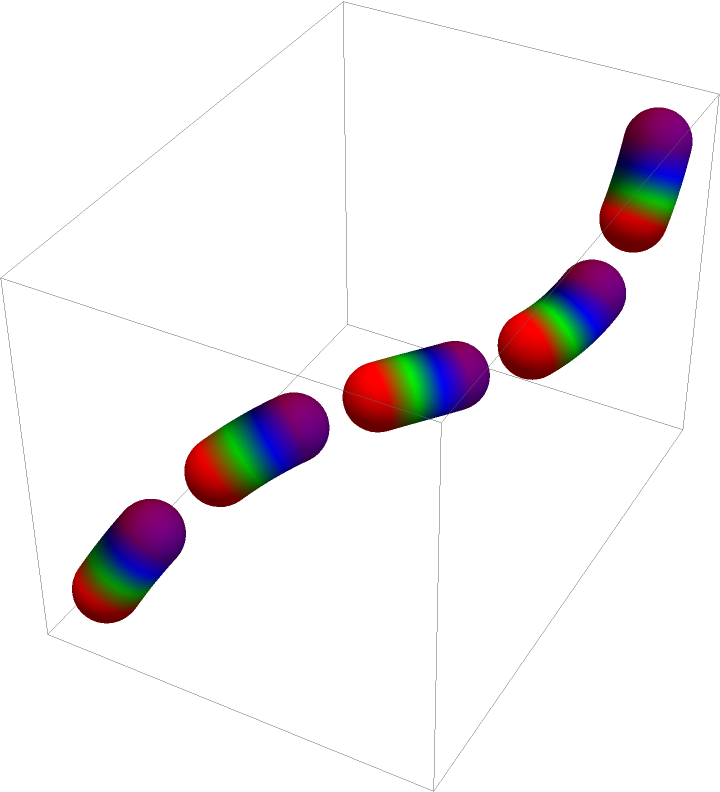 |
Single dashed tube segment:
| In[12]:= |
| Out[12]= | 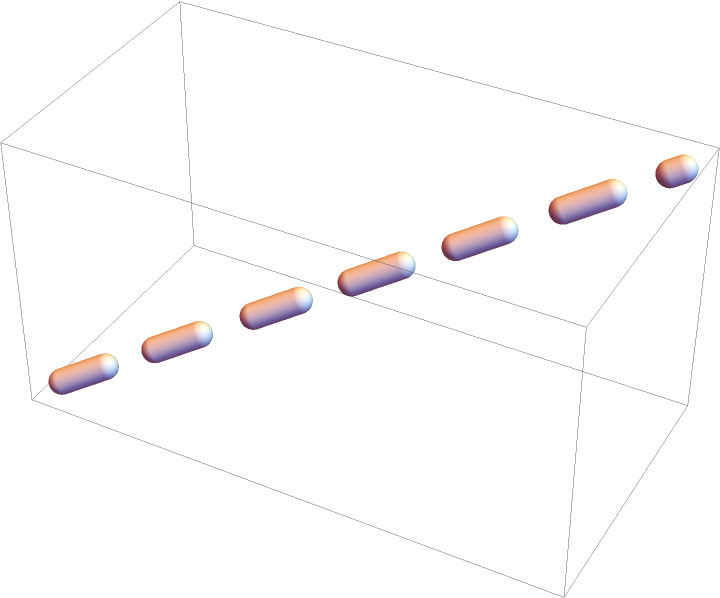 |
Multiple connected dashed tube segments:
| In[13]:= |
| Out[13]= | 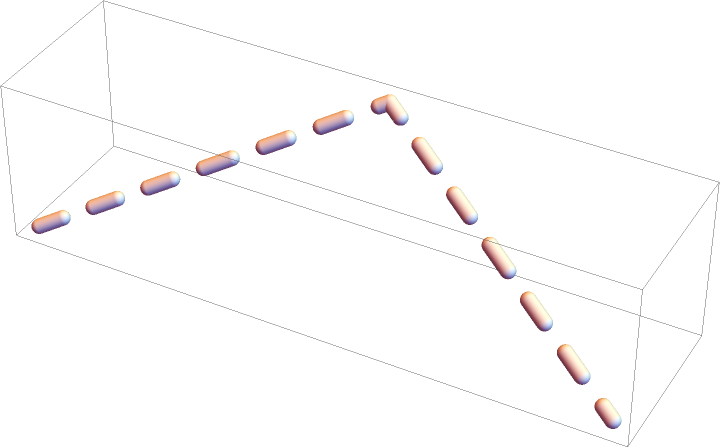 |
DashedTube can take a line or curve argument:
| In[14]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/3a0ac1ed-6eac-46cc-9dc8-2a6b9ae564cd"]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/1d2584a1e1d3621f.png) |
| Out[14]= |  |
Multiple disconnected dashed tube segments:
| In[15]:= |
| In[16]:= | ![{Graphics3D[ResourceFunction["DashedTube"][{s, s + 1}]], Graphics3D[
ResourceFunction["DashedTube"][BezierCurve[{s, s + 1, s + 2}]]], Graphics3D[
ResourceFunction["DashedTube"][
BSplineCurve[{s, s + 1, s + 2, s + 3}]]]}](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/72a0ba679816312f.png) |
| Out[16]= | 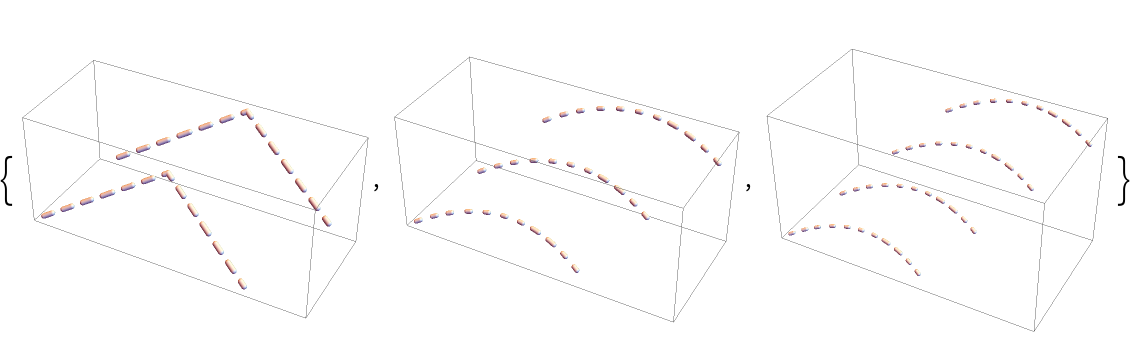 |
Use standard coordinates:
| In[17]:= | ![{Graphics3D[ResourceFunction["DashedTube"][{{0, 0, 0}, {2, 1, 1}}]], Graphics3D[
ResourceFunction["DashedTube"][
BSplineCurve[{{0, .2, 0}, {1, .8, 1}}]], Axes -> True]}](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/14ff4a5adfb9f387.png) |
| Out[17]= | 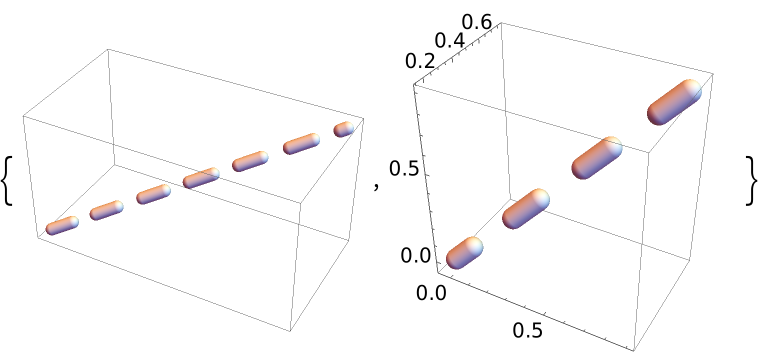 |
Use Scaled coordinates:
| In[18]:= | ![{Graphics3D[
ResourceFunction[
"DashedTube"][{Scaled[{0, 0, 0}], Scaled[{2, 1, 1}]}]], Graphics3D[
ResourceFunction["DashedTube"][
BSplineCurve[{Scaled[{0, .2, 0}], Scaled[{1, .8, 1}]}]], Axes -> True]}](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/67a32aef25555d31.png) |
| Out[18]= | 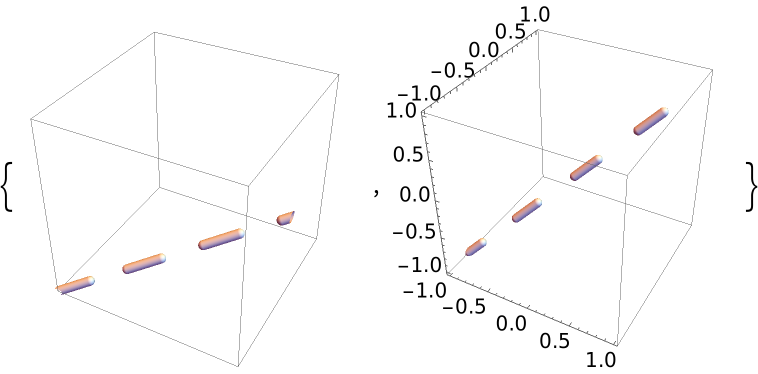 |
Dashed tubes with different radii:
| In[19]:= |
| In[20]:= |
| Out[20]= | 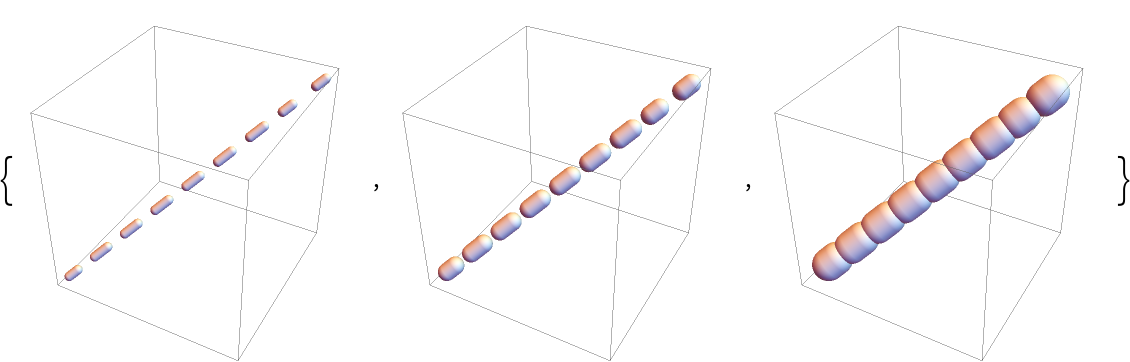 |
Radii can also be specified at vertices:
| In[21]:= | ![{Graphics3D[{CapForm[None], ResourceFunction["DashedTube"][{{0, 0, 0}, {1, 1, 1}}, {1, 2}]}], Graphics3D[{CapForm["Round"], ResourceFunction[
"DashedTube"][{{0, 0, 0}, 2 {-6, 4, 10}}, {2, 1}, {3, 2}]}]}](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/2680f7ededc71016.png) |
| Out[21]= | 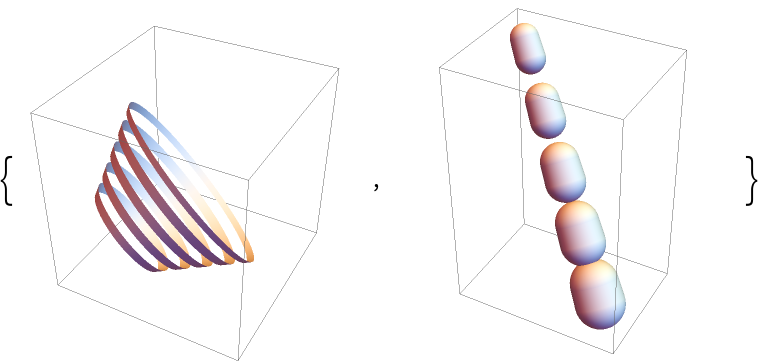 |
Dashed tubes with scaled radii:
| In[22]:= |
| In[23]:= |
| Out[23]= | 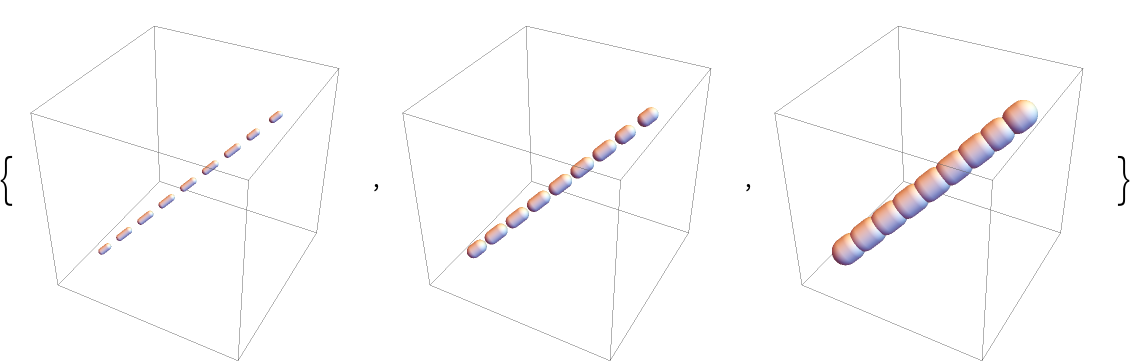 |
Use uniform dashing specified by 0.1:
| In[24]:= |
| Out[24]= | 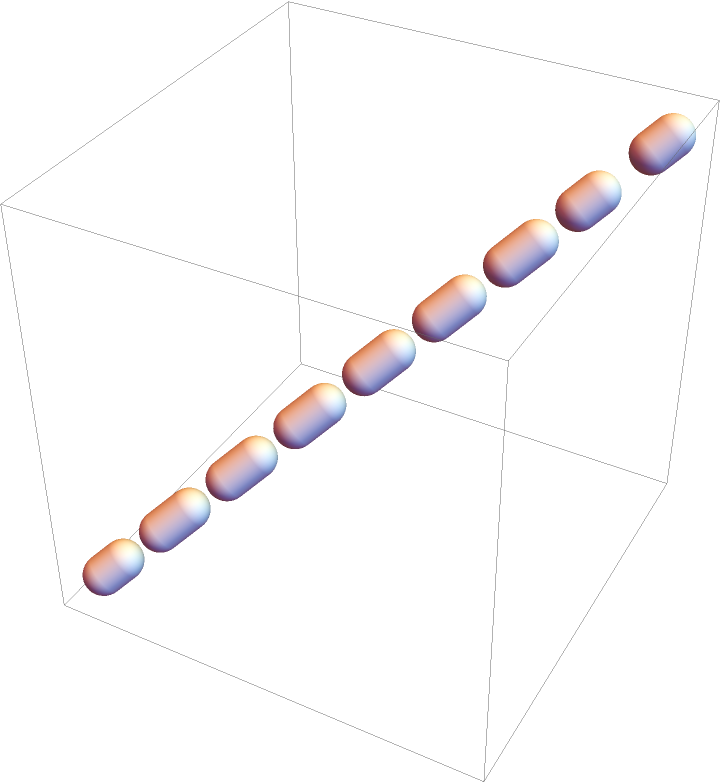 |
Use non-uniform dashing {0.25,0.1}:
| In[25]:= |
| Out[25]= | 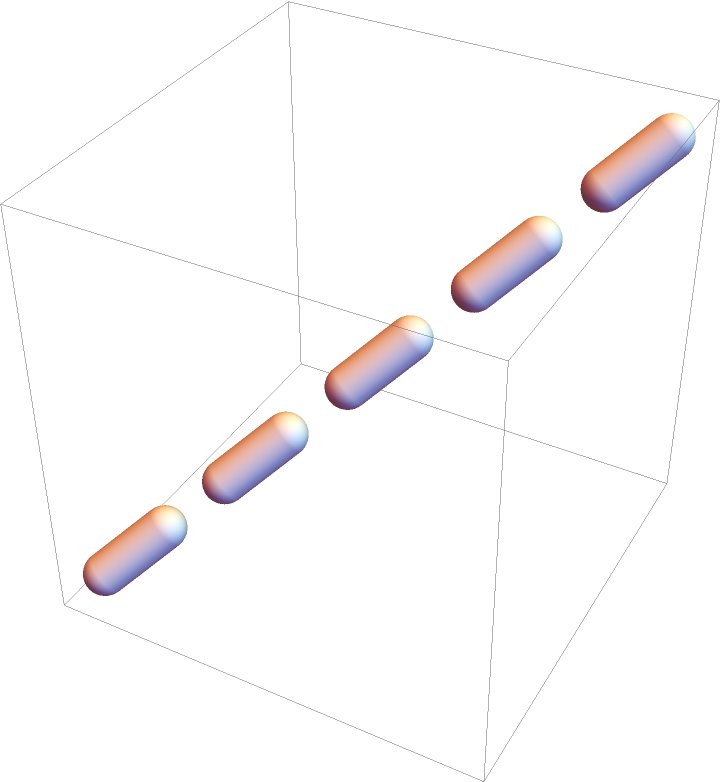 |
Use more complicated dashing {0.25,0.1,0.05}:
| In[26]:= |
| Out[26]= | 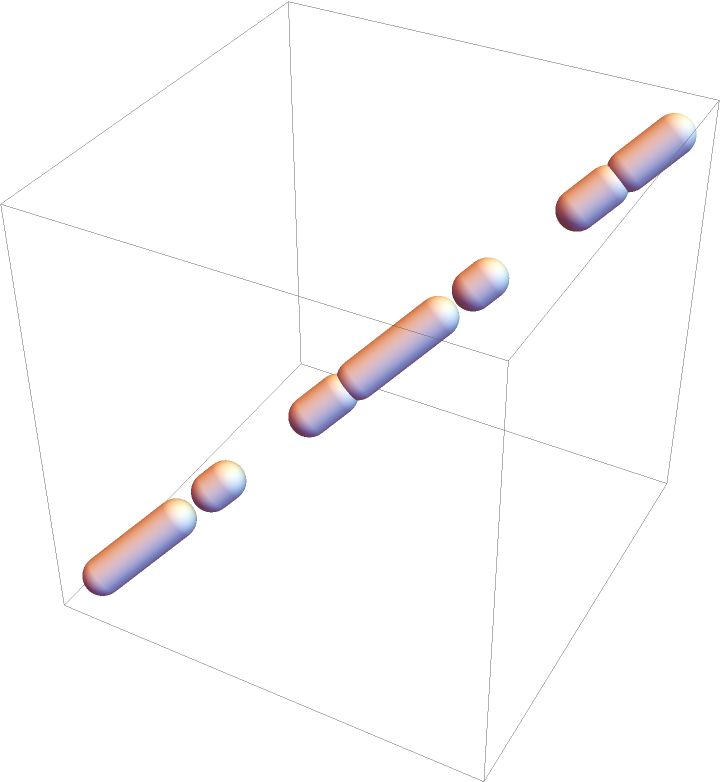 |
Dashing can also be specified outside DashedTube using Dashed, Dotted, DotDashed, Dashing, and AbsoluteDashing primitives:
| In[27]:= | ![{Graphics3D[{Dashed, ResourceFunction["DashedTube"][{{0, 0, 0}, {1, 1, 1}}, .01]}], Graphics3D[{Dashing[.05], ResourceFunction["DashedTube"][{{0, 0, 0}, {1, 1, 1}}, .01]}]}](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/537c7b5f839ec269.png) |
| Out[27]= | 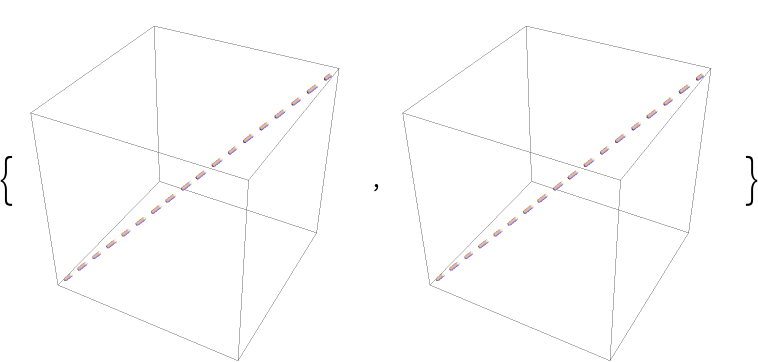 |
AbsoluteDashing[s] is internally automatically replaced with s:
| In[28]:= | ![{Graphics3D[{AbsoluteDashing[.05], ResourceFunction["DashedTube"][{{0, 0, 0}, {1, 1, 1}}, .01]}], Graphics3D[{ResourceFunction[
"DashedTube"][{{0, 0, 0}, {1, 1, 1}}, .01, 0.05]}]}](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/4ff4a2e3706213c4.png) |
| Out[28]= | 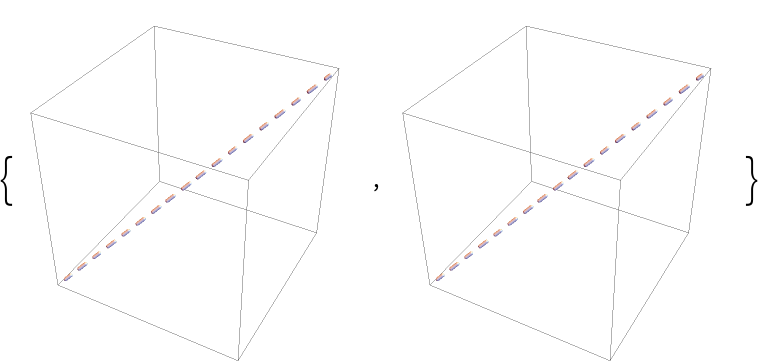 |
When both the external modifier such as Dashed and the explicit dashing specification inside DashedTube is used, the latter gets precedence:
| In[29]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/eb64a071-7144-46c3-8591-e563491a13cf"]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/39e64d6eaab3fc87.png) |
| Out[29]= | 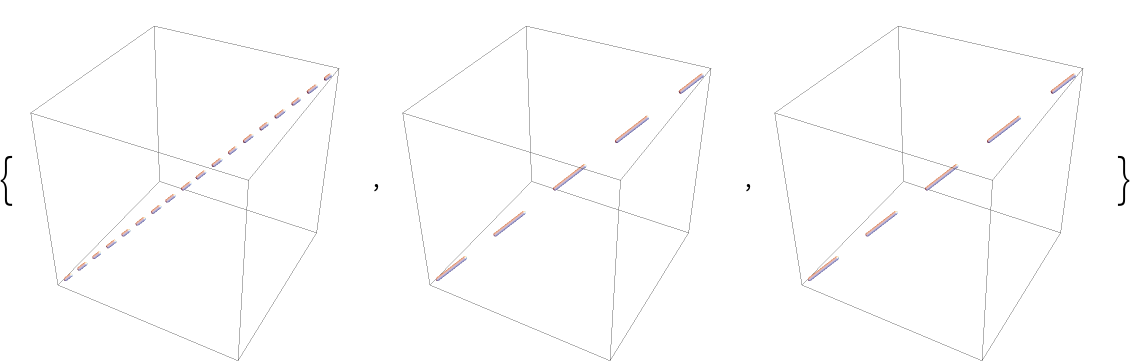 |
Colored dashed tubes:
| In[30]:= |
| In[31]:= |
| Out[31]= | 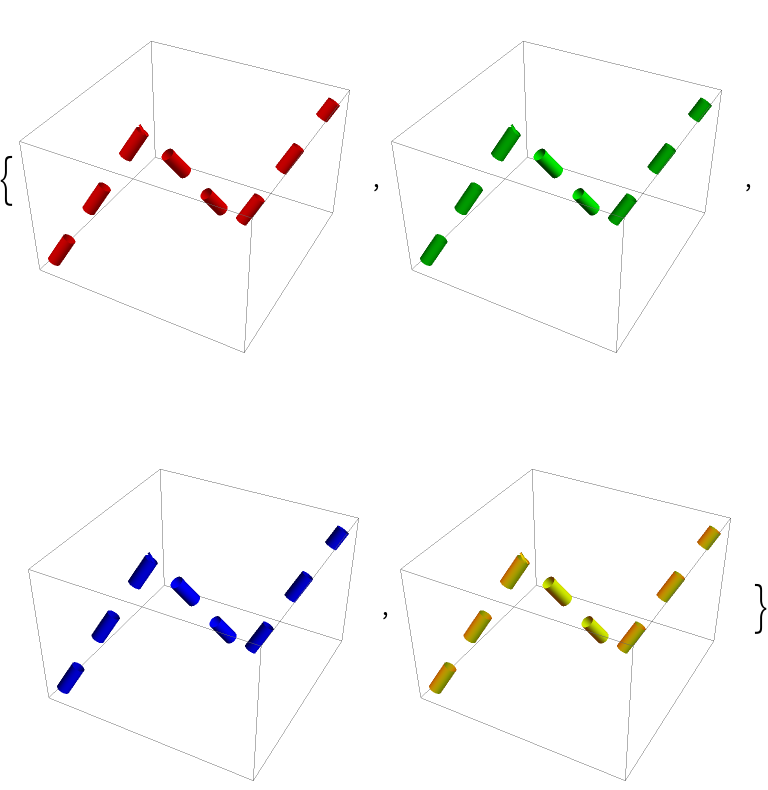 |
Different properties can be specified for the front and back faces using FaceForm:
| In[32]:= | ![Graphics3D[{FaceForm[Yellow, Blue], ResourceFunction["DashedTube"][10 {{0, 0, -1}, {0, 0, 1}}, 1, 2]}, PlotRange -> {{-1, 1}, {-.8, 1}, {-10, 7}}]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/52fdcf4f55d706b1.png) |
| Out[32]= |  |
Dashed tube caps can be specified using CapForm:
| In[33]:= | ![Table[Graphics3D[{CapForm[cap], ResourceFunction["DashedTube"][{{-1, 1, -1}, {1, -1/2, 1}}, 0.7, 0.5]}, PlotRange -> 2, PlotLabel -> Row[{cap}], Boxed -> False], {cap, {None, "Butt", "Round", "Square"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/0c3f7db7fa65315e.png) |
| Out[33]= | 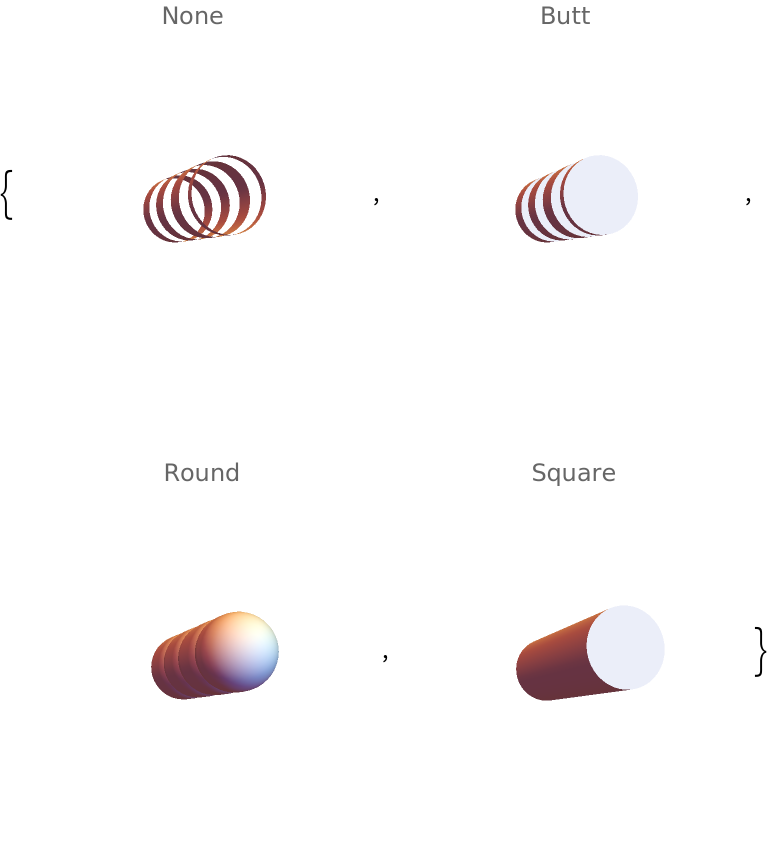 |
Joining of dashed tube segments can be specified using JoinForm:
| In[34]:= | ![Table[Graphics3D[{JoinForm[j], ResourceFunction[
"DashedTube"][{0.6 {-1, -1, -1}, {0, 0, 1}, {1, 1, -1}}, 0.3, 0.7]}, PlotRange -> 1.5, PlotLabel -> Row[{j}], Boxed -> False], {j, {None, "Bevel", "Round", "Miter"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/73d76a7898a5cda0.png) |
| Out[34]= | 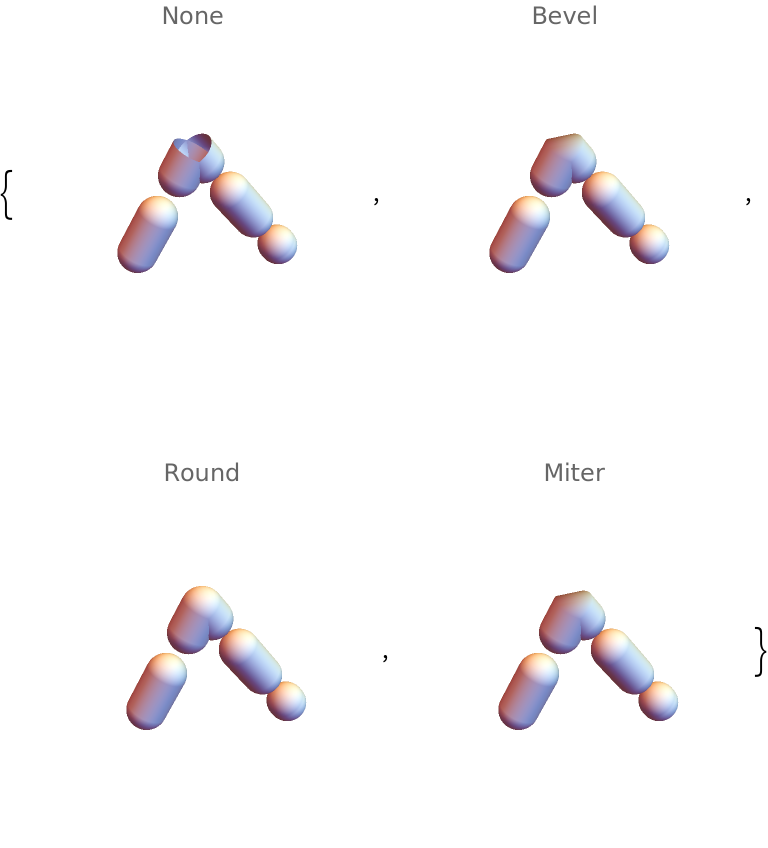 |
Colors can be specified at vertices using VertexColors:
| In[35]:= |
| Out[35]= | 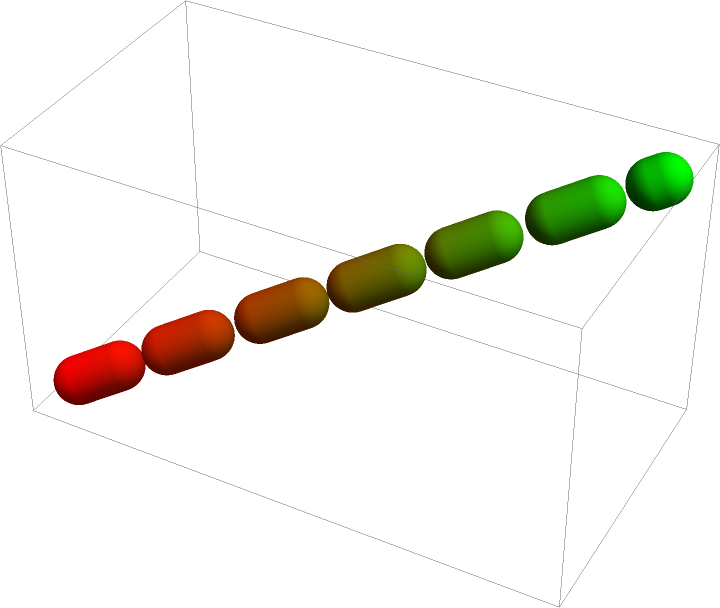 |
Specify color gradient over the tube:
| In[36]:= | ![Graphics3D[
ResourceFunction["DashedTube"][
BSplineCurve[{{0, 0, 0}, {0, 2, 1}, {-1, 0, 1}}], VertexColors -> {Red, Green, Blue}]]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/2672558c2d91b999.png) |
| Out[36]= | 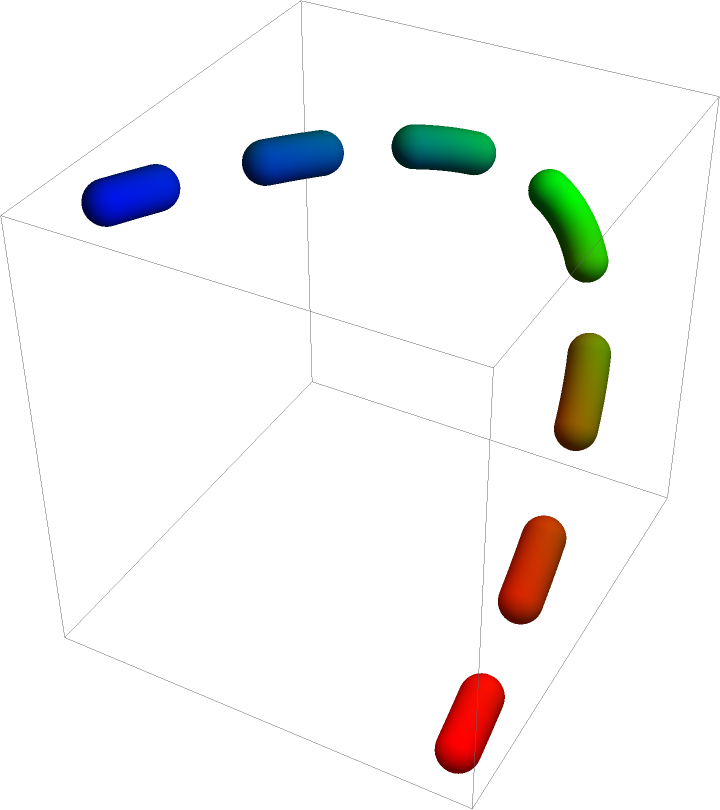 |
Use the same gradient for each segment separately:
| In[37]:= | ![Graphics3D[
ResourceFunction["DashedTube"][
BSplineCurve[{{0, 0, 0}, {0, 2, 1}, {-1, 0, 1}}], VertexColors -> {Red, Green, Blue}, "Each" -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/2496c14f72341472.png) |
| Out[37]= | 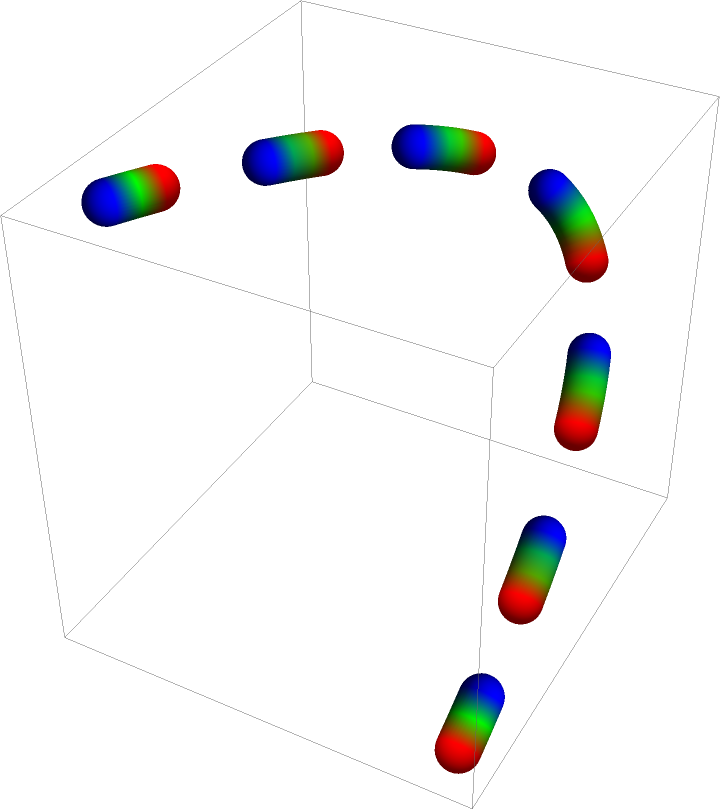 |
By default, the styling as well as Arrow are applied to the DashedTube globally:
| In[38]:= | ![g1 = Graphics3D[
ResourceFunction["DashedTube"][
BSplineCurve[{{0, 0, 0}, {0, 2, 1}, {-1, 0, 1}}], 0.05, {0.2, 0.1}, VertexColors -> {Red, Green, Blue}]];
g2 = Graphics3D[{Arrowheads[.2], Arrow@ResourceFunction["DashedTube"][
BSplineCurve[{{-1, 0, 1}, {0, 2, 1}, {0, 0, 0}}], 0.05, {0.2, 0.25}]}];
{g1, g2}](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/24c402930f5e1cf3.png) |
| Out[38]= | 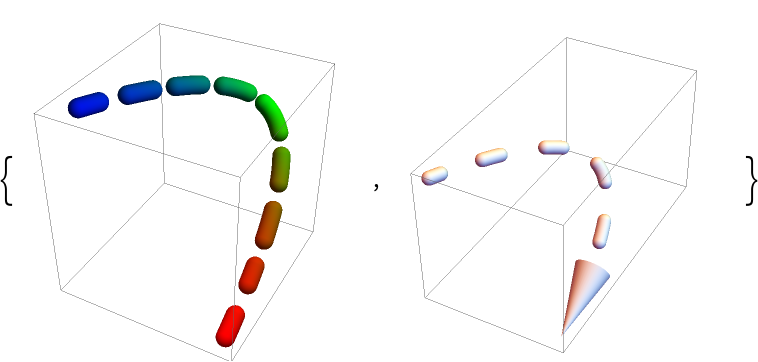 |
To apply the styling and arrows to each segment separately, set "Each" to True:
| In[39]:= | ![g1 = Graphics3D[
ResourceFunction["DashedTube"][
BSplineCurve[{{0, 0, 0}, {0, 2, 1}, {-1, 0, 1}}], 0.05, {0.2, 0.1}, VertexColors -> {Red, Green, Blue}, "Each" -> True]];
g2 = Graphics3D[{Arrowheads[.15], Arrow@ResourceFunction["DashedTube"][
BSplineCurve[{{-1, 0, 1}, {0, 2, 1}, {0, 0, 0}}], 0.05, {0.2, 0.25}, "Each" -> True]}];
{g1, g2}](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/2bd8026454c70408.png) |
| Out[39]= | 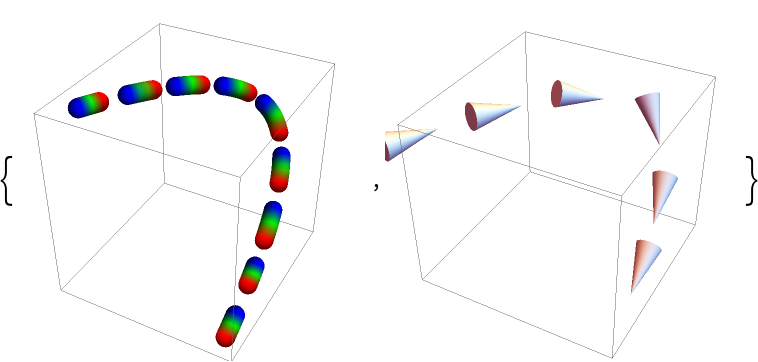 |
To apply an arrow to each segment of a DashedTube that has a global styling, use a simple replacement:
| In[40]:= | ![gr = {Arrowheads[.15], ResourceFunction["DashedTube"][
BSplineCurve[{{-1, 0, 1}, {0, 2, 1}, {0, 0, 0}}], 0.05, {0.2, 0.25}, VertexColors -> {Red, Green, Blue}]};](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/65cda7119c88f5ed.png) |
| In[41]:= |
| Out[41]= | 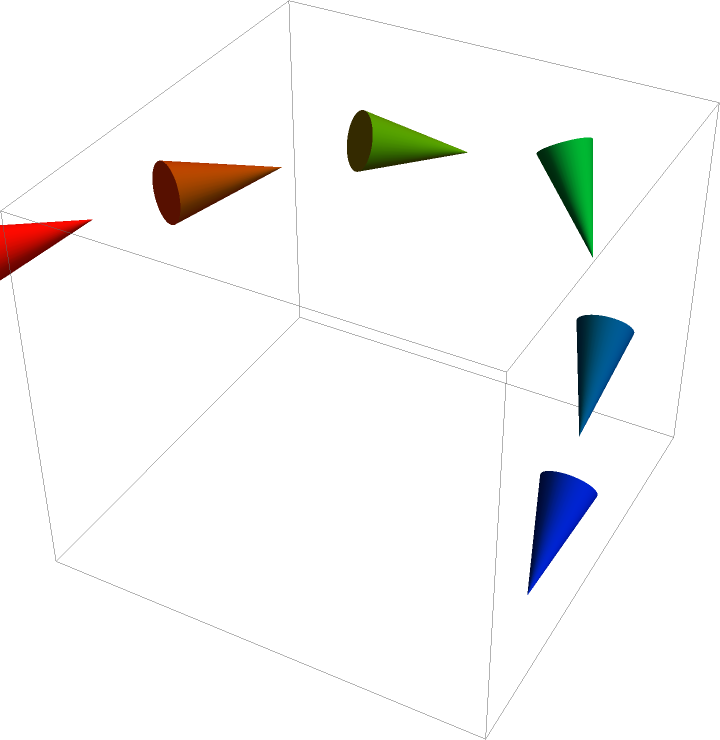 |
For some combinations of curves and dashing specifications, the sampling process may introduce aliasing artifacts or cusps:
| In[42]:= | ![Graphics3D[
ResourceFunction["DashedTube"][
BSplineCurve[{{0, 0, 0}, {0, 5, 0}, {1, 1, -1}}], 0.05, {0.5, 0.2}, PlotPoints -> 20, MaxIterations -> 1]]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/569354746d1f49c9.png) |
| Out[42]= | 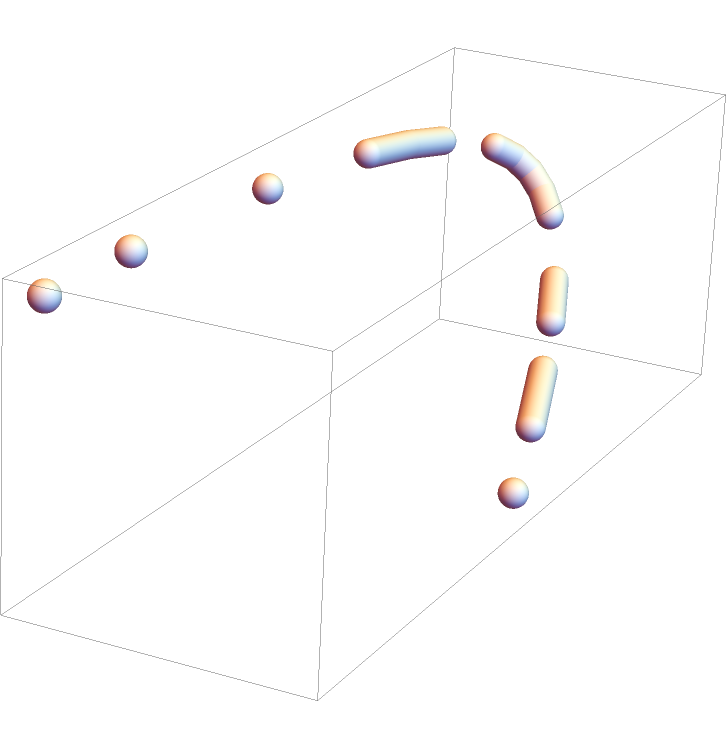 |
Increase the initial number of sampling points:
| In[43]:= | ![gr = Graphics3D[
ResourceFunction["DashedTube"][
BSplineCurve[{{0, 0, 0}, {0, 5, 0}, {1, 1, -1}}], 0.05, {0.5, 0.2},
PlotPoints -> 150, MaxIterations -> 1]]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/4d015f638b2a2410.png) |
| Out[43]= | 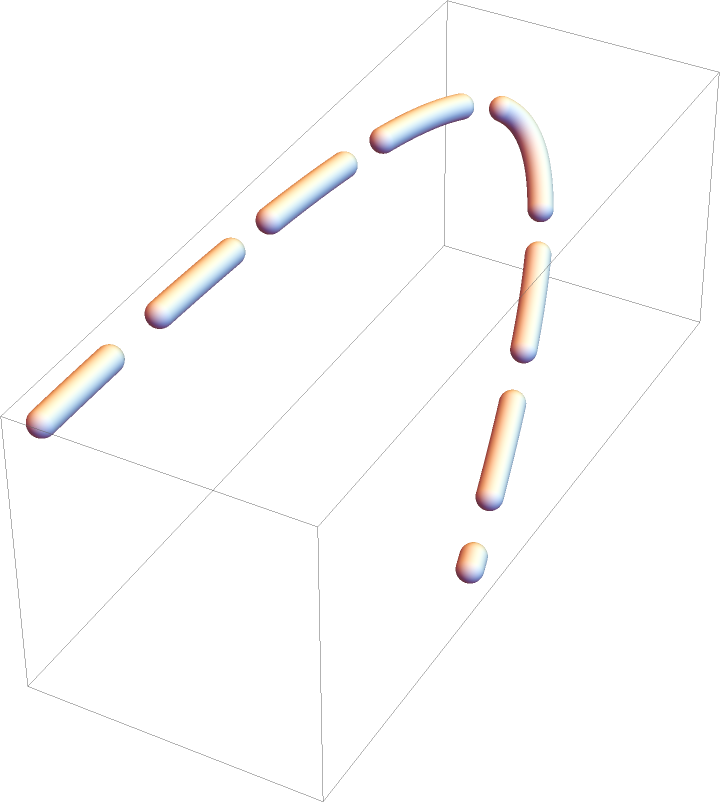 |
Manual setting of the sampling number may lead to excessive number of resulting points that make up the tube segments:
| In[44]:= |
| Out[44]= |
For some combinations of curves and dashing specifications, the sampling process may introduce aliasing artifacts or cusps:
| In[45]:= | ![Graphics3D[
ResourceFunction["DashedTube"][
BSplineCurve[{{0, 0, 0}, {0, 5, 0}, {1, 1, -1}}], 0.05, {0.5, 0.2}, PlotPoints -> 20, MaxIterations -> 1]]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/0ea034437ab0b7b5.png) |
| Out[45]= | 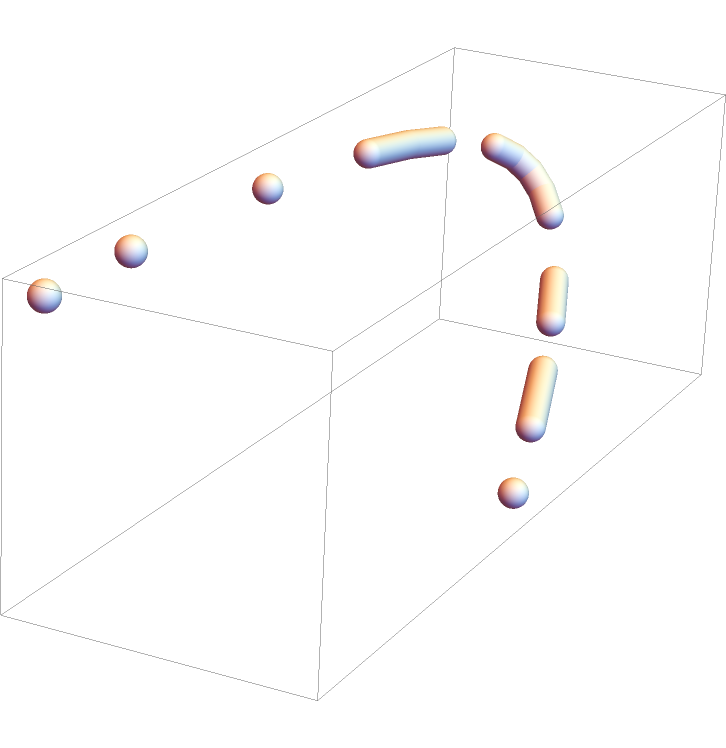 |
Increase the number of division steps in the sampling process to adaptively find an optimum number of sampling points:
| In[46]:= | ![gr = Graphics3D[
ResourceFunction["DashedTube"][
BSplineCurve[{{0, 0, 0}, {0, 5, 0}, {1, 1, -1}}], 0.05, {0.5, 0.2},
PlotPoints -> 10, MaxIterations -> 10]]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/4b80c655bd27b2b8.png) |
| Out[46]= | 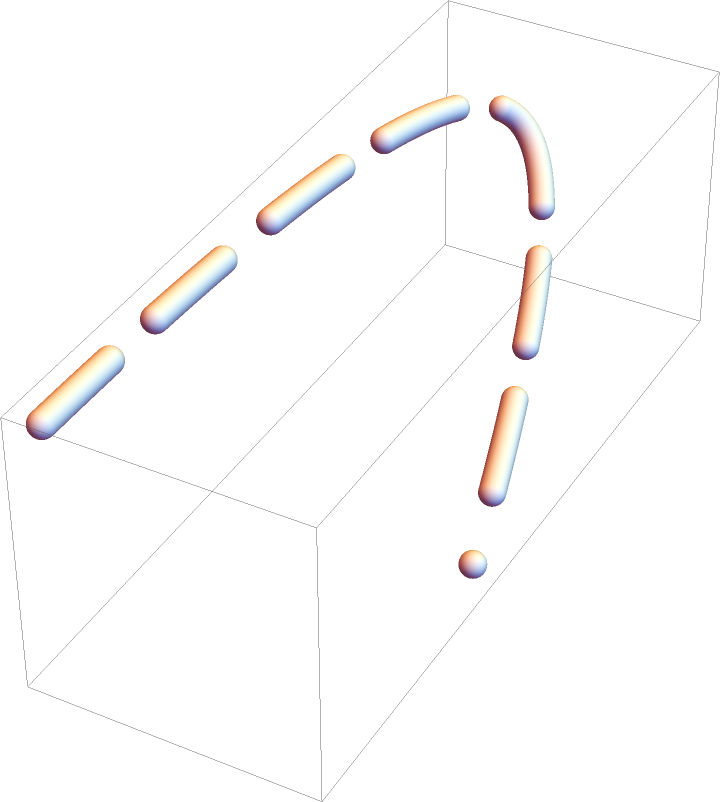 |
The number of points that make up the tube segments is chosen to be minimum and still sufficient:
| In[47]:= |
| Out[47]= |
Plot a parametric space curve and replace the curve with a dashed tube:
| In[48]:= |
| Out[48]= | 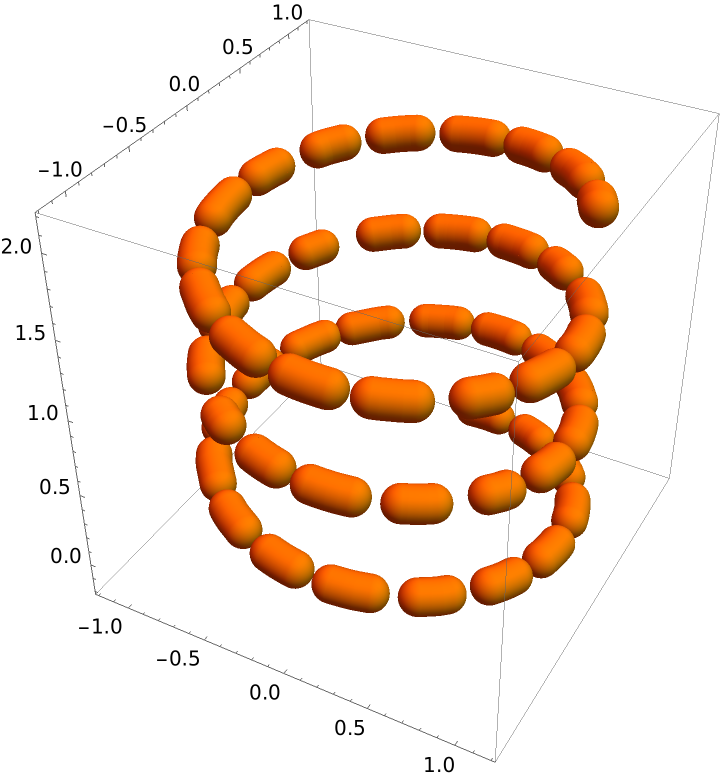 |
DashedTube can be used with Arrow for dashed 3D arrows:
| In[49]:= | ![Graphics3D[{Arrowheads[.2], Blue, Arrow[ResourceFunction["DashedTube"][{{0, 0, 0}, {2, 1, 1}}, 0.05, {0.35, 0.3}, VertexColors -> {Red, Blue}]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/008ebae5872364ae.png) |
| Out[49]= | 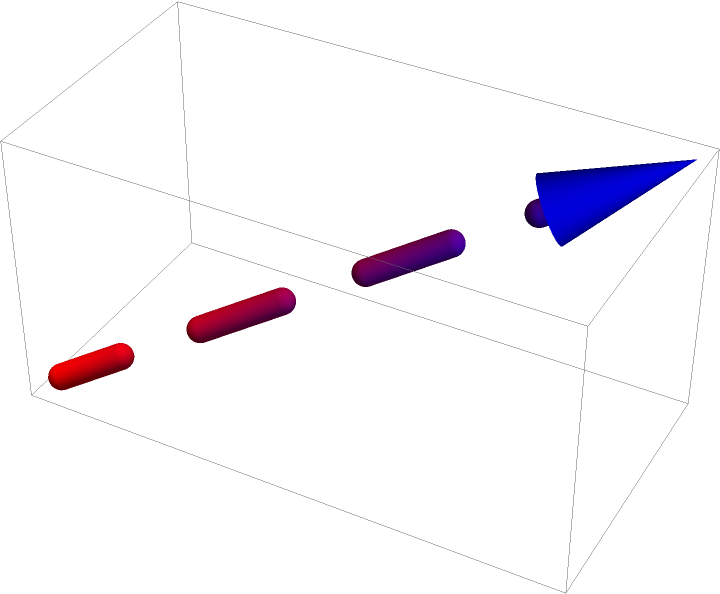 |
Define a 3D coordinate system with dashed axes:
| In[50]:= | ![Graphics3D[{Dashing[{0.07, .05}], Gray, ResourceFunction[
"DashedTube"][{{{-1, 0, 0}, {1, 0, 0}}, {{0, -1, 0}, {0, 1, 0}}, {{0, 0, -1}, {0, 0, 1}}}, .02]}]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/35cf3ad36922ff8d.png) |
| Out[50]= | 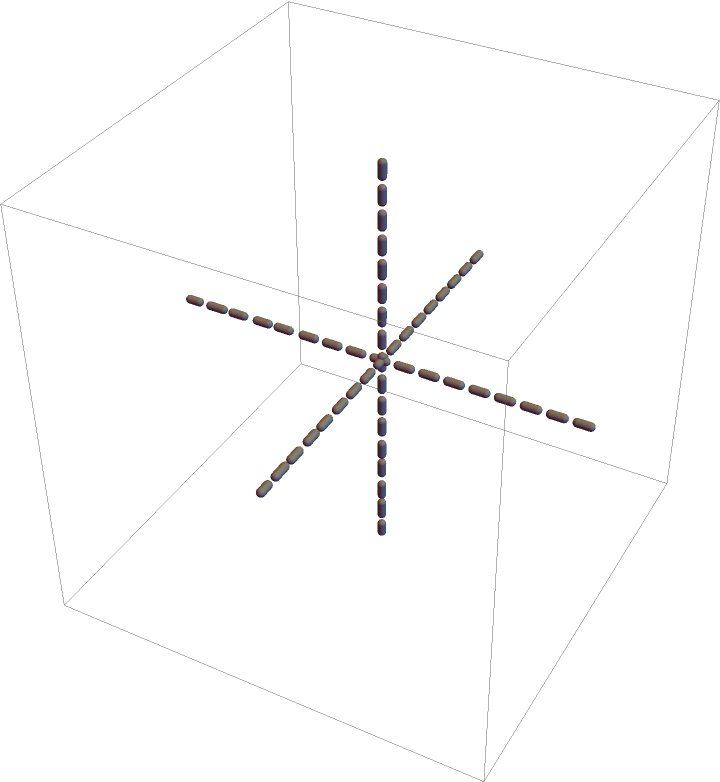 |
When no dashing is specified, the DashedTube gives identical results to Tube:
| In[51]:= | ![{Graphics3D[
ResourceFunction["DashedTube"][{{0, 0, 0}, {2, 1, 1}}, 0.02, 0]], Graphics3D[Tube[{{0, 0, 0}, {2, 1, 1}}, 0.02]]}](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/2af70716ed3767a4.png) |
| Out[51]= | 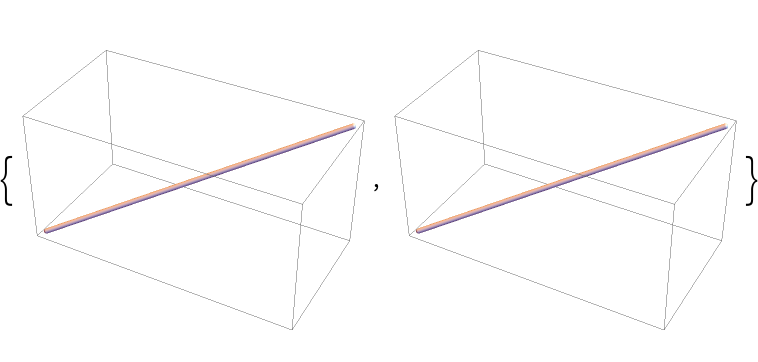 |
Use Arrow with DashedTube to get a dashed 3D arrow:
| In[52]:= |
| Out[52]= | 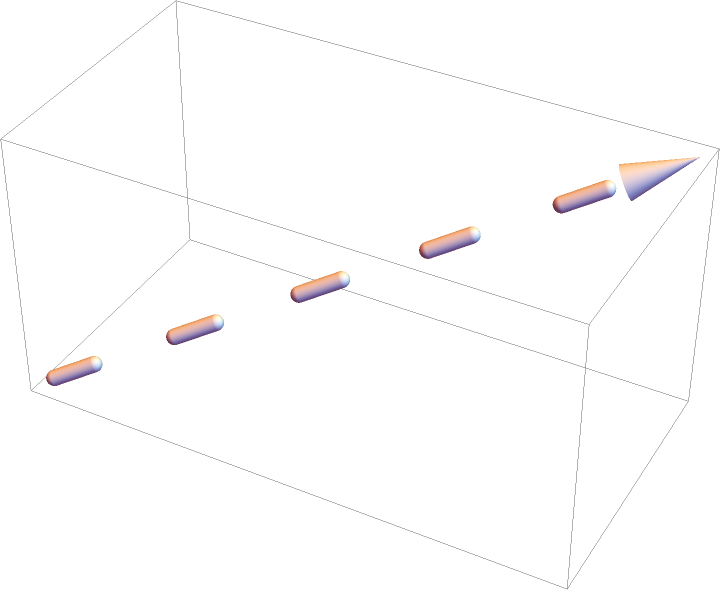 |
Use Dashing specification outside DashedTube to set its dashing:
| In[53]:= |
| Out[53]= | 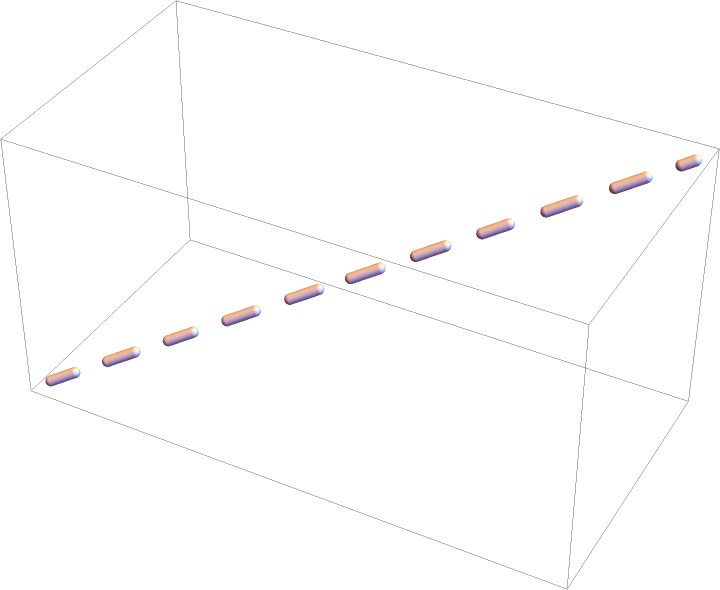 |
Use dashing primitives Dashed, Dotted, and DotDashed to specify the dashing:
| In[54]:= | ![Table[Graphics3D[{dashing, ResourceFunction["DashedTube"][{{0, 0, 0}, {1, 1, 1}}, .01]}, ImageSize -> Medium], {dashing, {Dashed, Dotted, DotDashed}}]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/5f3f80a682e63b17.png) |
| Out[54]= | 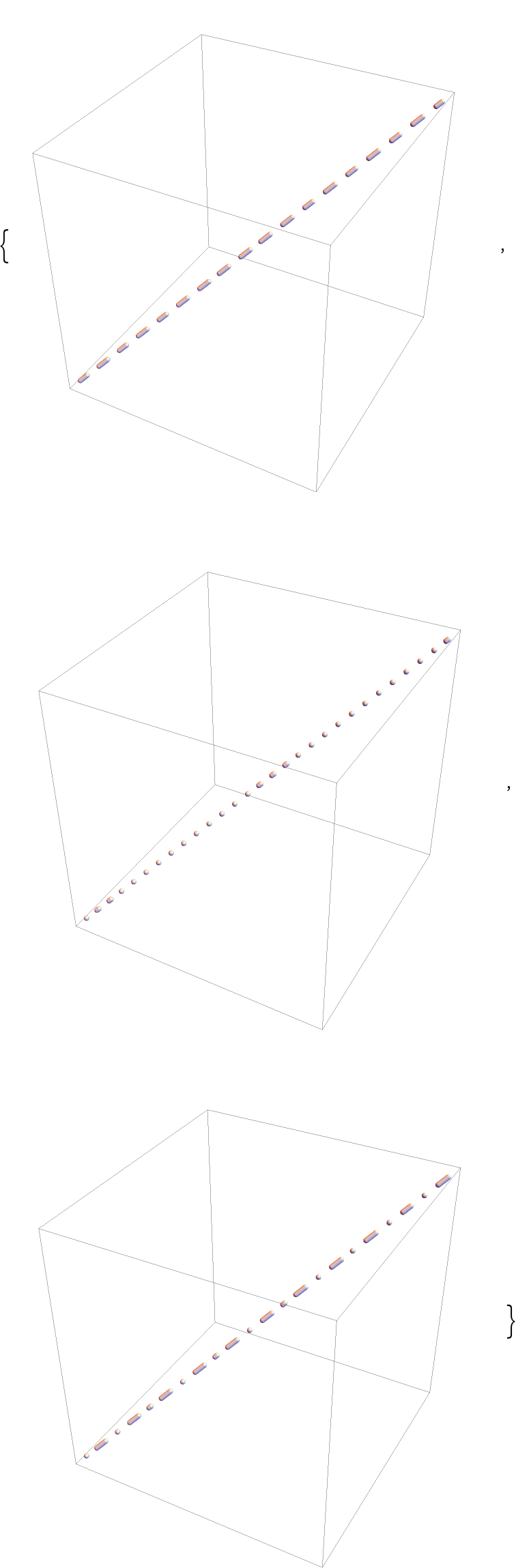 |
One can readily mimic the action of DashedTube, provided the uniformity of the dashing is not an issue:
| In[55]:= | ![dashedLineSimple[curve_, rad_, dashing_] := Module[{pts, dashlist = dashing, fun = curve},
If[Head[dashlist] =!= List, dashlist = {dashlist}];
dashlist = Join @@ Table[dashlist, 1/Total[dashlist]];
dashlist = Join[{0.}, Most@Accumulate[dashlist]]; fun = fun /. {BezierCurve -> BezierFunction, BSplineCurve -> BSplineFunction}; pts = Partition[Table[fun[n], {n, dashlist}], 2][[;; ;; 2]];
Tube[#, rad] & /@ pts
]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/2ff0c44bc4776339.png) |
| In[56]:= | ![curve1 = BezierCurve[{{0, 0, 0}, {1/2, 1/2, 1}, {1, 1, 1}}];
curve2 = BezierCurve[{{0, 0, 0}, {5, 10, 1/2}, {1, 1, 2}}];
{Graphics3D[dashedLineSimple[curve1, .01, .05]], Graphics3D[dashedLineSimple[curve2, .05, {0.06, 0.001}]]}](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/5afa4ba2743121d8.png) |
| Out[56]= | 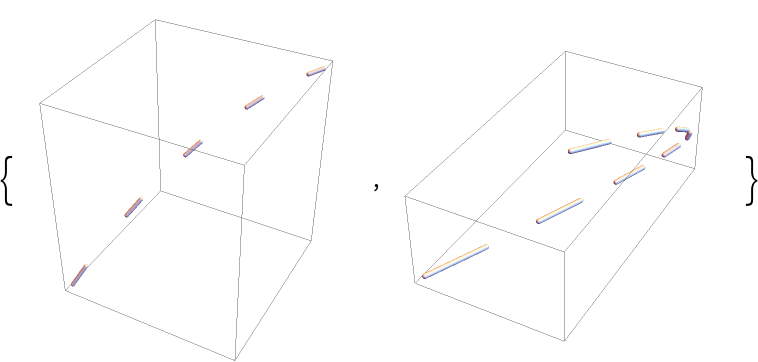 |
DashedTube tries to keep the dashing uniform:
| In[57]:= | ![{Graphics3D[
ResourceFunction["DashedTube"][curve1, .01, {0.15, 0.25}]], Graphics3D[ResourceFunction["DashedTube"][curve2, .05, {0.8, 0.4}]]}](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/2111c4a4fe115ced.png) |
| Out[57]= | 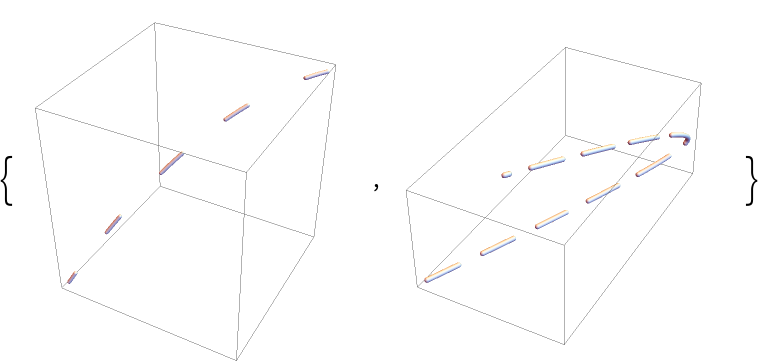 |
In some cases, aliasing artifacts may occur:
| In[58]:= |
| Out[58]= | 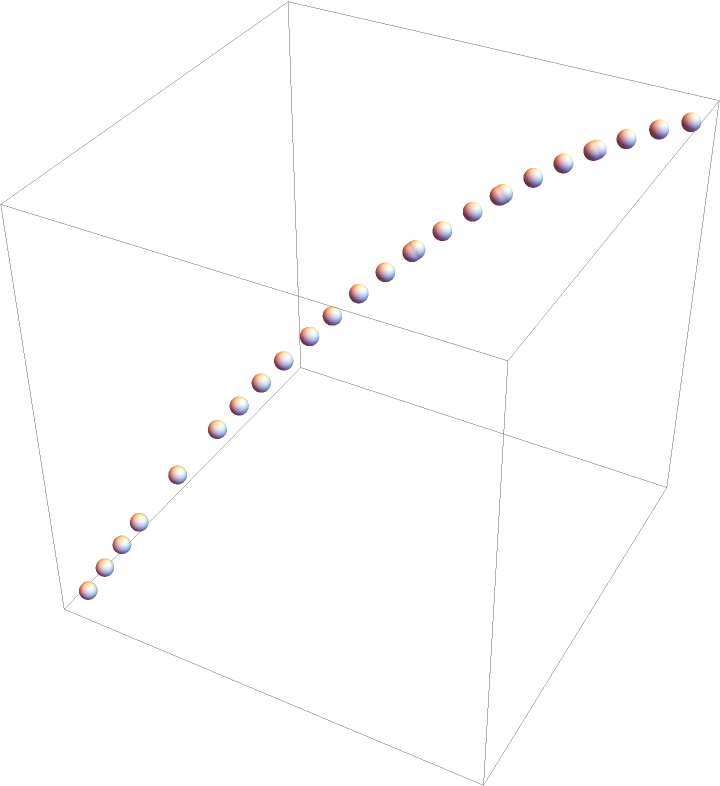 |
Increase the number of sampling iterations:
| In[59]:= | ![Graphics3D[
ResourceFunction["DashedTube"][
BezierCurve[{{0, 0, 0}, {1/2, 1/2, 1}, {1, 1, 1}}], .02, {.01, .06},
MaxIterations -> 50]]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/2314647e8469dbf1.png) |
| Out[59]= | 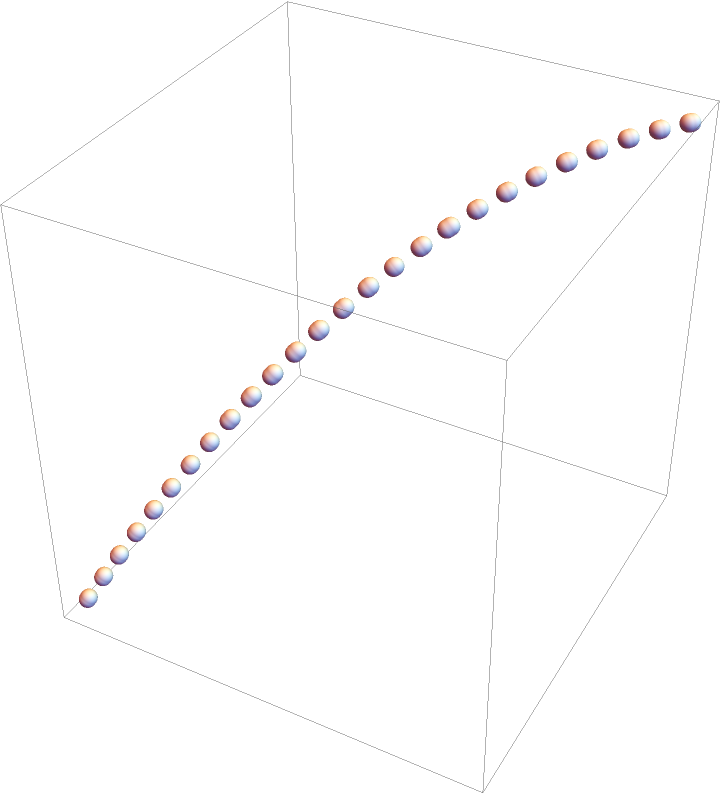 |
From the way how the built-in arrows are handled, undesired behavior may occur when DashedTube is used with Arrow:
| In[60]:= | ![Graphics3D[{Arrowheads[.3], Arrow[ResourceFunction["DashedTube"][{{0, 0, 0}, {2, 1, 1}}, 0.1, {0.2, 0.2}, VertexColors -> {Red, Blue}]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/5b95199f046a99aa.png) |
| Out[60]= | 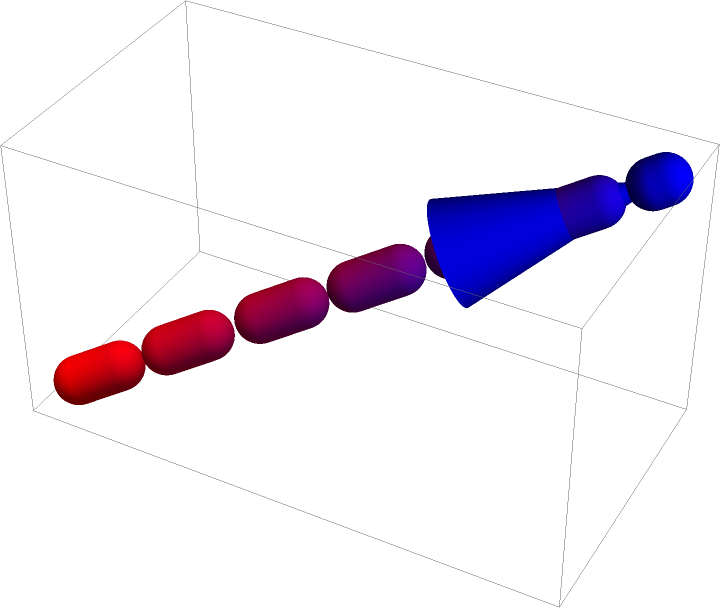 |
This effect can be mitigated by removing several last segments from the dashed tube:
| In[61]:= | ![gr = {Arrow[
ResourceFunction["DashedTube"][{{0, 0, 0}, {2, 1, 1}}, 0.1, {0.2, 0.2}, VertexColors -> {Red, Blue}]]};
segments = Cases[gr, {{_, _Tube} ..}, Infinity];
arrows = Cases[gr, {{_, _Arrow} ..}, Infinity];](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/3f94d6743f6c4c13.png) |
| In[62]:= |
| Out[62]= | 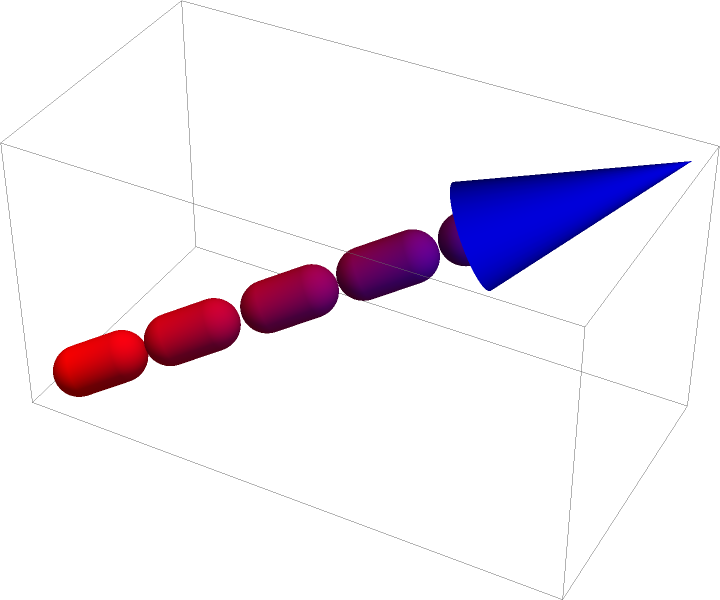 |
When Arrow is used together with VertexColors and "Each"→True, the color gradients are ignored and only the last color is used for each segment:
| In[63]:= |
| In[64]:= |
| Out[64]= | 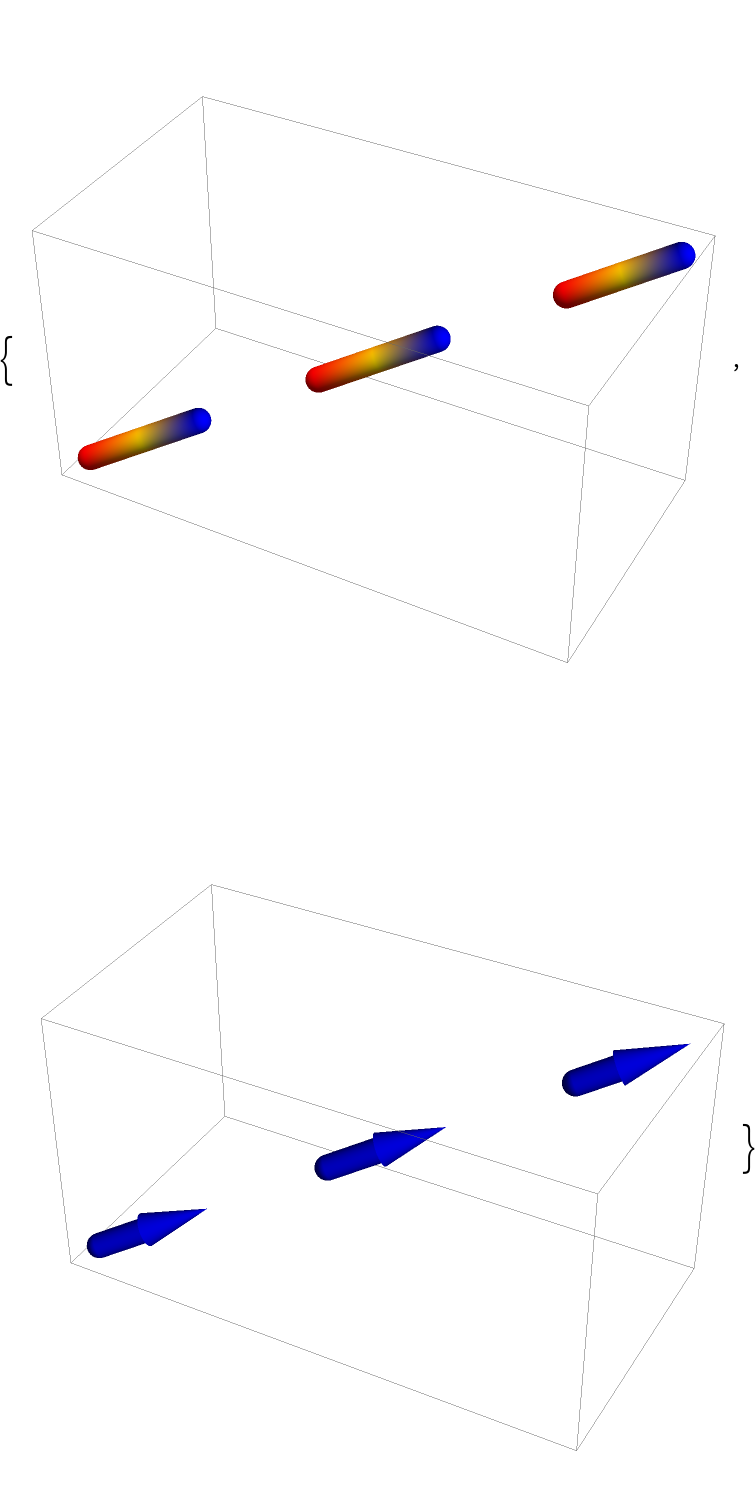 |
DashedTube makes no difference between the dashing specified using absolute and standard units:
| In[65]:= | ![{Graphics3D[{AbsoluteDashing[.05], ResourceFunction["DashedTube"][{{0, 0, 0}, {1, 1, 1}}, .01]}], Graphics3D[{Dashing[.05], ResourceFunction["DashedTube"][{{0, 0, 0}, {1, 1, 1}}, .01]}]}](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/291836364c06fd24.png) |
| Out[65]= | 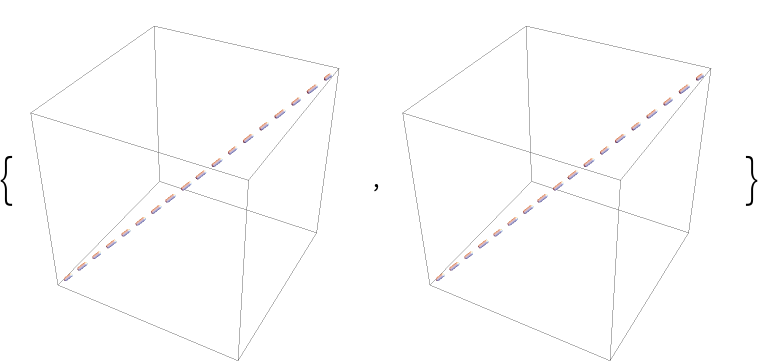 |
Compare this with the default behavior for Line:
| In[66]:= |
| Out[66]= | 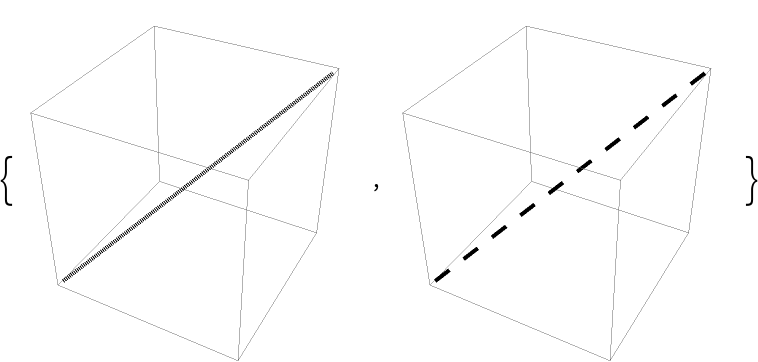 |
When JoinForm is set to "Miter", the result may not be discernible from that for "Bevel":
| In[67]:= | ![tube = ResourceFunction[
"DashedTube"][{{-1, -1, -1}, {0, 0, 1}, {1, 1, -1}}, 0.3, {1.2, 0.8}, PlotPoints -> 10, MaxIterations -> 5];
Table[Graphics3D[{JoinForm[j], tube}, PlotRange -> 1.5, PlotLabel -> Row[{j}], Boxed -> False], {j, {None, "Bevel", "Round", "Miter"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/50c0a0b02841528f.png) |
| Out[67]= | 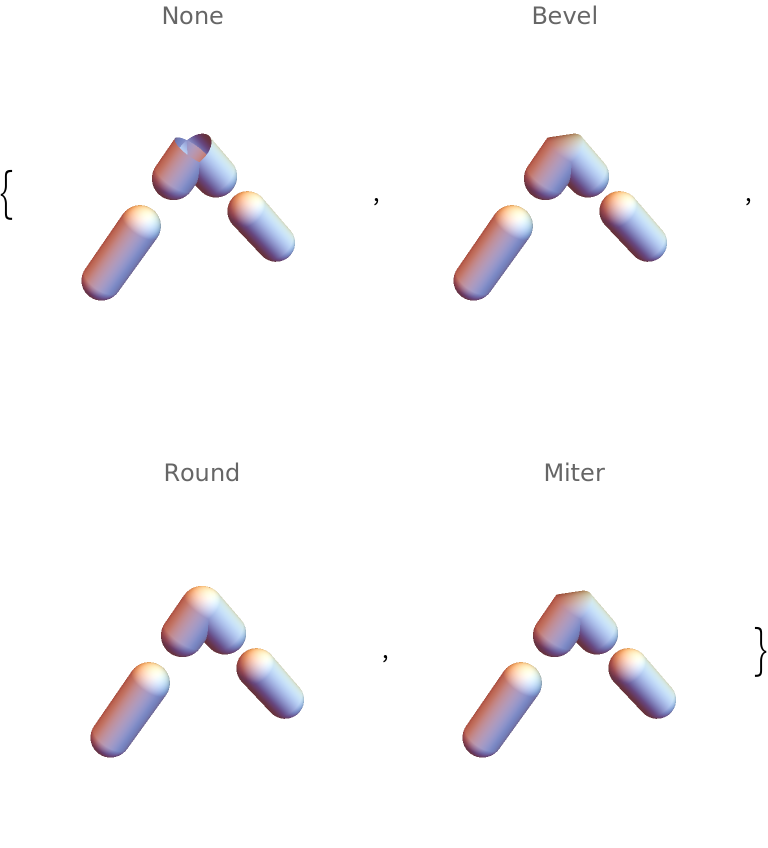 |
The reason is that the dashed tube consists of many points and the joints are effectively smooth, resulting in no visible cusp:
| In[68]:= |
| In[69]:= |
| Out[69]= | 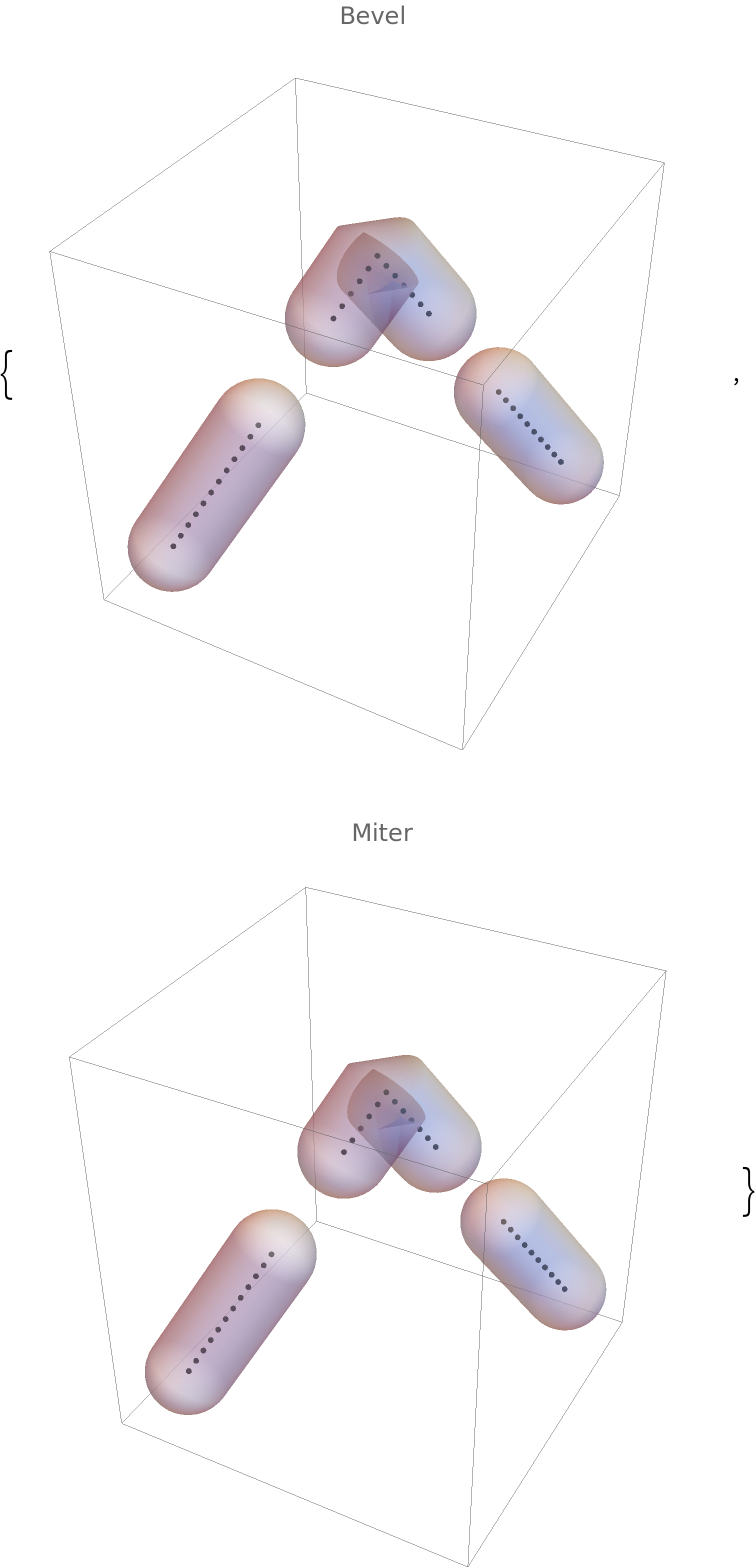 |
When only the essential points are retained, one recovers the expected behavior:
| In[70]:= | ![ptsr1 = pts[[1]];
ptsr2 = pts[[2, {1, 6, -1}]];
ptsr3 = pts[[3]];](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/0ad0dd01b2d613b3.png) |
| In[71]:= | ![Table[Graphics3D[{Point /@ {ptsr1, ptsr2, ptsr3}, Opacity[.5], JoinForm[j], Tube[{ptsr1, ptsr2, ptsr3}, 0.3]}, ImageSize -> Medium, PlotLabel -> j], {j, {"Bevel", "Miter"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/10e0ae00a8812e05.png) |
| Out[71]= | 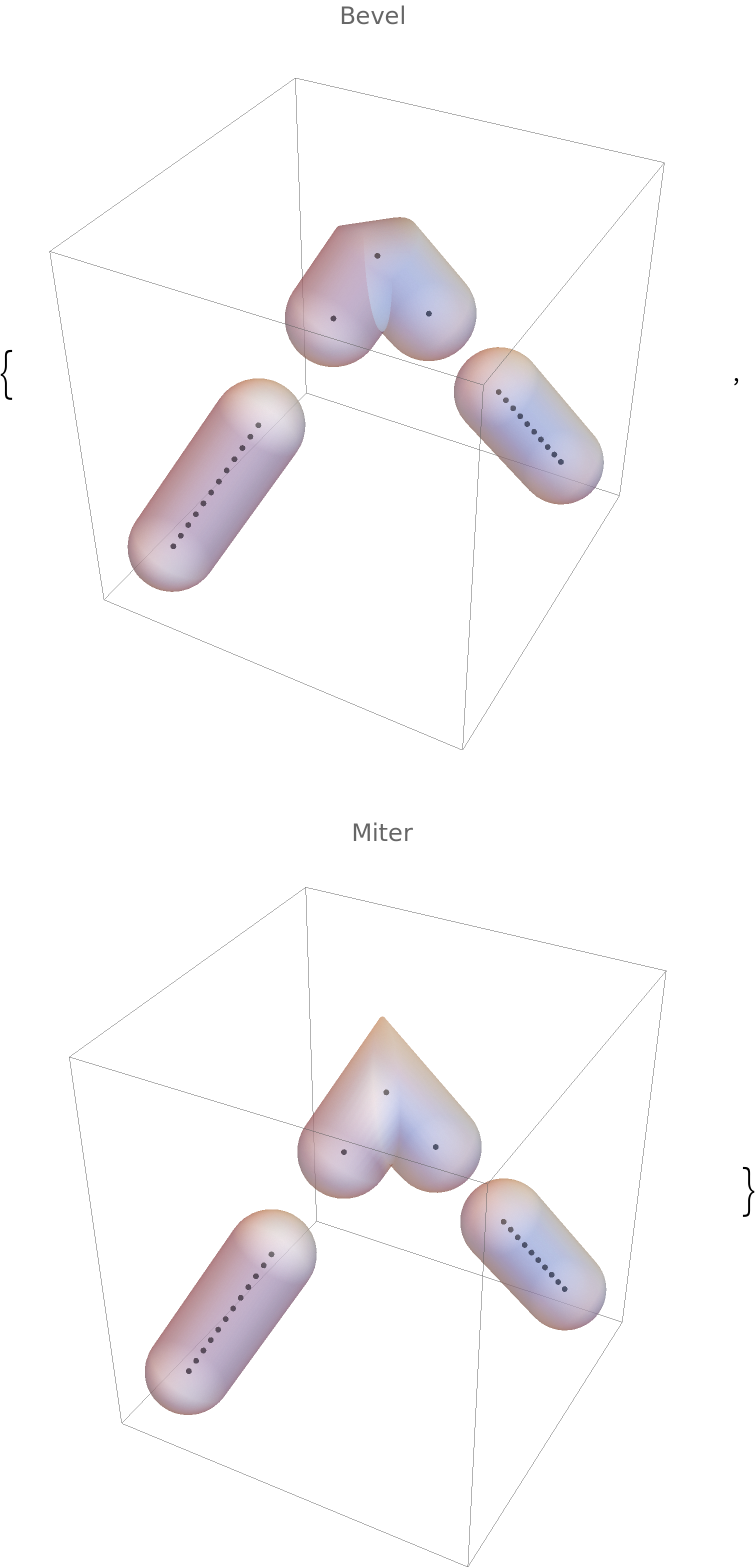 |
The external dashing specification has to be in the same List with DashedTube, otherwise it is ignored:
| In[72]:= | ![Graphics3D[{Dashing[{.1, .5, .2}],
{Red, ResourceFunction["DashedTube"][{{0, 0, 0}, {1, 1, 1}}]},
{Green, ResourceFunction["DashedTube"][{{1, 0, 0}, {-1, 1, 1}}]}
}]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/577f4756dafa69c0.png) |
| Out[72]= | 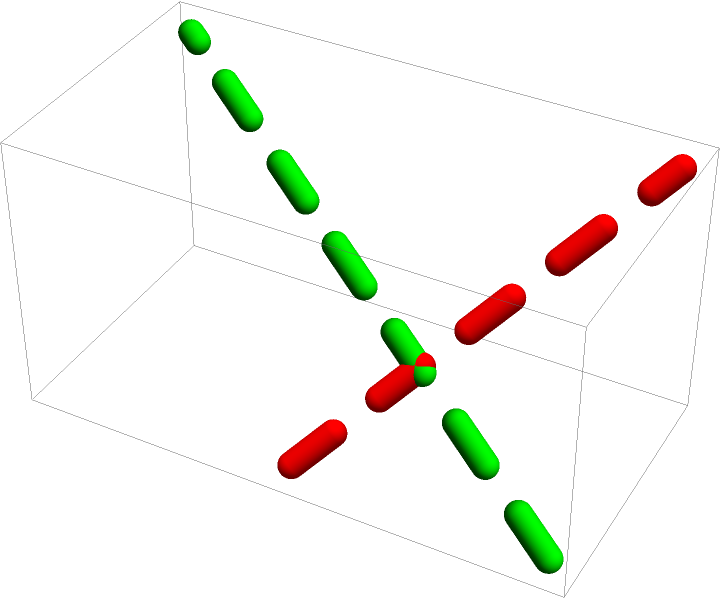 |
Flatten the whole list:
| In[73]:= | ![Graphics3D[{Dashing[{.1, .5, .2}],
Red, ResourceFunction["DashedTube"][{{0, 0, 0}, {1, 1, 1}}],
Green, ResourceFunction["DashedTube"][{{1, 0, 0}, {-1, 1, 1}}]
}]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/2deb56477c47efc9.png) |
| Out[73]= | 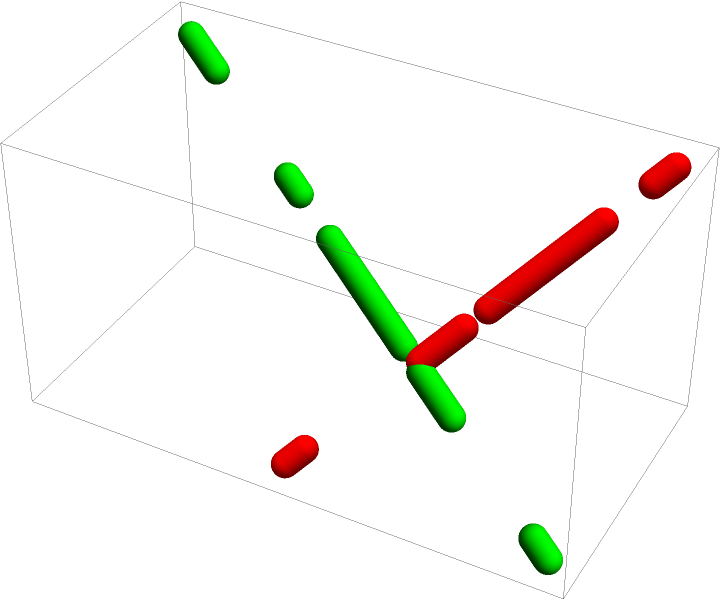 |
Alternatively, put the Dashing construct into each sublist:
| In[74]:= | ![Graphics3D[{
{Dashing[{.1, .5, .2}], Red, ResourceFunction["DashedTube"][{{0, 0, 0}, {1, 1, 1}}]},
{Dashing[{.1, .5, .2}], Green, ResourceFunction["DashedTube"][{{1, 0, 0}, {-1, 1, 1}}]}
}]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/53b48fd1e239520b.png) |
| Out[74]= | 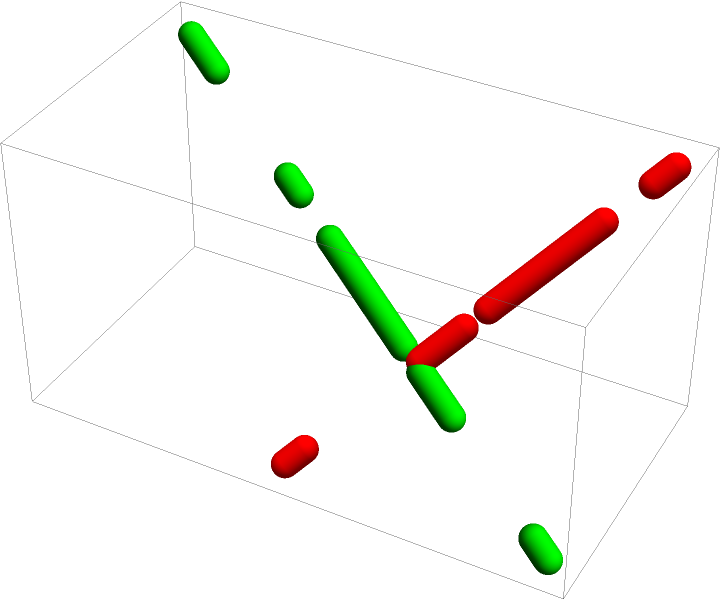 |
Dashed tube curves with interpolated radii:
| In[75]:= | ![Graphics3D[{CapForm[None], ResourceFunction["DashedTube"][
BSplineCurve[{{0, 0, -1}, {0, 0, -.5}, {0, 0, 0}, {0, 0, 1}, {0, 0,
15}, {0, 0, 20}, {0, 0, 25}, {0, 0, 32}, {0, 0, 35}}], {6, 6.5,
6, 3.2, 12, 4, 2, 2.4, 3.5}, 0.8]}]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/3649e1bffbf0632a.png) |
| Out[75]= | 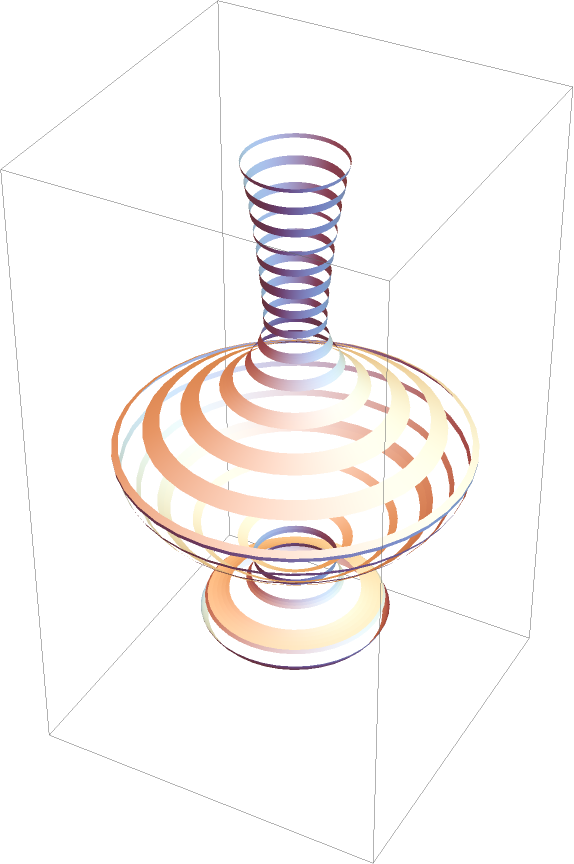 |
Using random radii:
| In[76]:= |
| In[77]:= | ![Graphics3D[{
{Red, ResourceFunction["DashedTube"][
BSplineCurve[pts, SplineDegree -> 3], .5 RandomReal[1, 31], {2, 1}, PlotPoints -> 250]},
{Green, ResourceFunction["DashedTube"][
BSplineCurve[pts, SplineDegree -> 8], .5 RandomReal[1, 31], {2, 1}, PlotPoints -> 250]}
}, PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/763cc869bf7146a5.png) |
| Out[77]= | 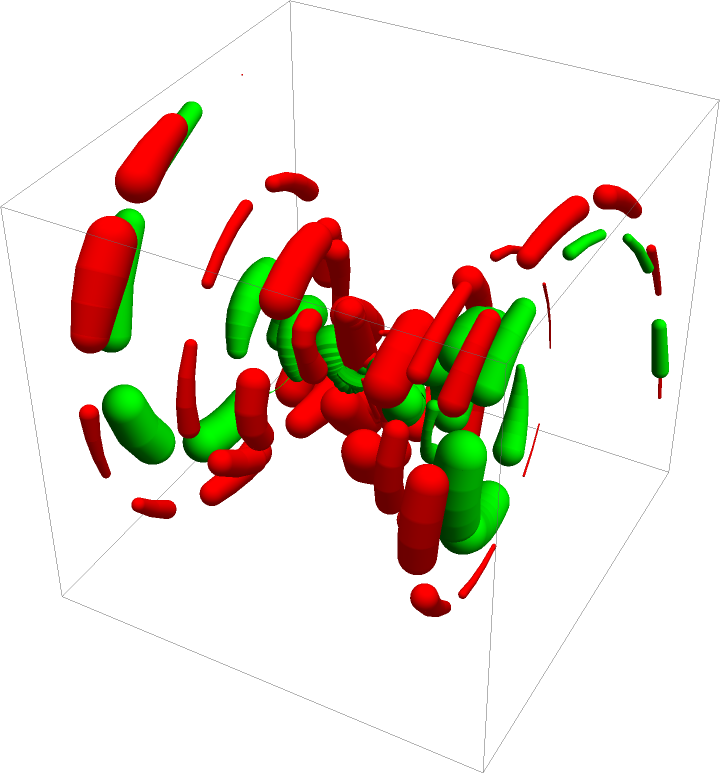 |
Create a curve composed of balls:
| In[78]:= |
| In[79]:= | ![Graphics3D[{Dashing[{.1, 1}], Red, ResourceFunction["DashedTube"][BSplineCurve[pts, SplineDegree -> 3],
Reverse@Subdivide[0.1, .5, Length[pts] - 1], PlotPoints -> 1500, MaxIterations -> 1]}]](https://www.wolframcloud.com/obj/resourcesystem/images/c8b/c8b3362f-5dd0-4a36-981a-ea8b591fc56a/78d2a2e000060f26.png) |
| Out[79]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License