Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generates the evolution of a cyclic tag system
|
ResourceFunction["CyclicTagSystemEvolveList"][rules,init,t] returns the list of states attained from evolving init, using cyclic tag system rules over t steps. |
|
|
ResourceFunction["CyclicTagSystemEvolveList"][rules,init,t,dt] returns the states attained at every step dt. |
|
|
ResourceFunction["CyclicTagSystemEvolveList"][rules,init,t,dt,prop] returns the specified prop of states attained at every step. |
| "States" | the list of tape configurations throughout the cyclic tag system evolution |
| "Lengths" | the list of tape lengths throughout the cyclic tag system evolution |
Generate the tape states in 25 evolution steps of a cyclic tag system:
| In[1]:= |
|
| Out[1]= |

|
Return only every fifth state in that same evolution:
| In[2]:= |
|
| Out[2]= |
|
Find the length of every tenth state in the cyclic tag evolution:
| In[3]:= |
|
| Out[3]= |
|
Visualize the successive tape states in the evolution of a cyclic tag system:
| In[4]:= |
|
| Out[4]= |

|
Plot how tape length changes across the evolution of the same cyclic tag system:
| In[5]:= |
![ListStepPlot[
ResourceFunction["CyclicTagSystemEvolveList"][{{1, 1}, {1, 0}}, {1}, 500, 1, "Lengths"], Filling -> Axis]](https://www.wolframcloud.com/obj/resourcesystem/images/c65/c65f8900-e280-4db9-aee5-fc866a61c05d/1-0-0/4bce996f5343a822.png)
|
| Out[5]= |
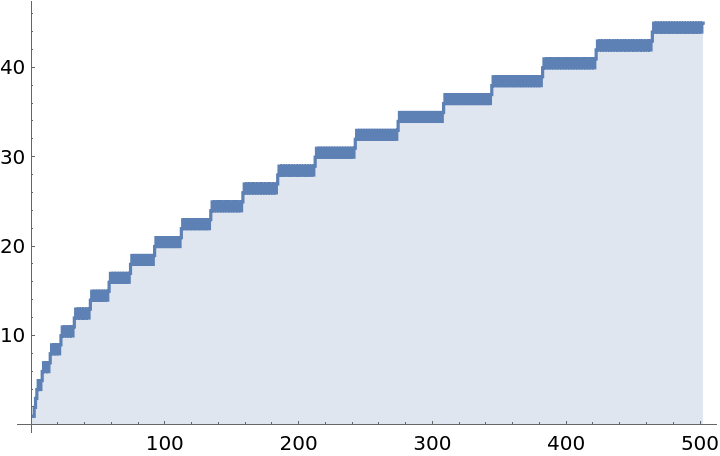
|
Visualize the successive tape states in the evolution of a slightly more complicated cyclic tag system:
| In[6]:= |
![ArrayPlot[
PadRight[ResourceFunction["CyclicTagSystemEvolveList", ResourceVersion->"1.0.0"][{{0, 1}, {0}, {0, 1, 1}}, {0, 1, 1, 1}, 25], Automatic, 0.25]]](https://www.wolframcloud.com/obj/resourcesystem/images/c65/c65f8900-e280-4db9-aee5-fc866a61c05d/1-0-0/263c1a06f23d8c5e.png)
|
| Out[6]= |

|
Plot how tape length changes across the evolution of the same cyclic tag system (which in this case demonstrates that the system eventually halts):
| In[7]:= |
![ListStepPlot[
ResourceFunction["CyclicTagSystemEvolveList", ResourceVersion->"1.0.0"][{{0, 1}, {0}, {0, 1, 1}}, {0, 1, 1, 1}, 200, 1, "Lengths"], Filling -> Axis]](https://www.wolframcloud.com/obj/resourcesystem/images/c65/c65f8900-e280-4db9-aee5-fc866a61c05d/1-0-0/3831c8971ab76c1e.png)
|
| Out[7]= |
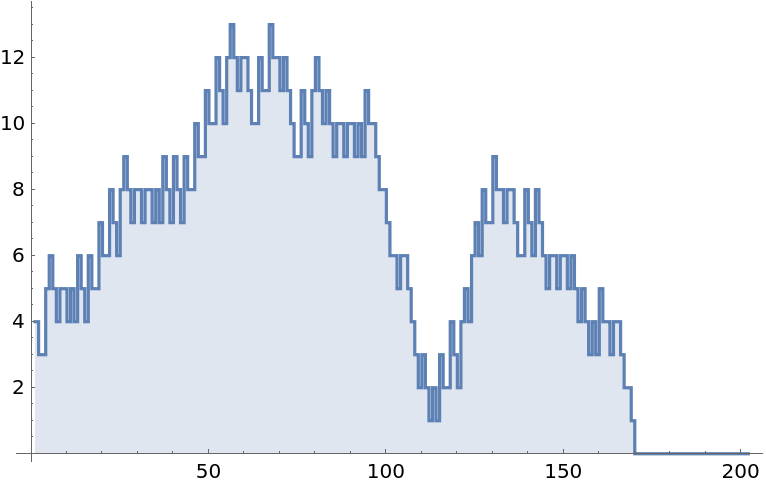
|
This work is licensed under a Creative Commons Attribution 4.0 International License