Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a cubic B-spline curve that passes through given points
ResourceFunction["CubicSplineCurve"][{{x1,y1,…},{x2,y2,…},…}] constructs a cubic interpolating BSplineCurve that passes through the given set of points. |
A list of points:
| In[1]:= |
Show the points along with an interpolating cubic B-spline:
| In[2]:= | ![Graphics[{{Directive[AbsoluteThickness[3], ColorData[97, 1]], ResourceFunction["CubicSplineCurve"][pts]}, {Directive[
AbsolutePointSize[6], ColorData[97, 4]], Point[pts]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/d48/d4868462-3a51-4922-a30e-dcd3b58d6943/6de5026d211a5c29.png) |
| Out[2]= |  |
Choose six points in the plane to be interpolated:
| In[3]:= |
Use CubicSplineCurve with Arrow:
| In[4]:= | ![Graphics[{{Directive[ColorData[97, 5], Arrowheads[Medium]], Arrow[ResourceFunction["CubicSplineCurve"][pts]]}, {Directive[
ColorData[97, 3], AbsolutePointSize[4]], Point[pts]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/d48/d4868462-3a51-4922-a30e-dcd3b58d6943/69075c16ac17ef10.png) |
| Out[4]= |  |
Choose 3D points to be interpolated:
| In[5]:= |
Show the points along with an interpolating cubic B-spline:
| In[6]:= | ![Graphics3D[{{Directive[AbsoluteThickness[3], ColorData[97, 1]], ResourceFunction["CubicSplineCurve"][pts]}, {Directive[
AbsolutePointSize[6], ColorData[97, 4]], Point[pts]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/d48/d4868462-3a51-4922-a30e-dcd3b58d6943/31aa74f8afe1a9e1.png) |
| Out[6]= | 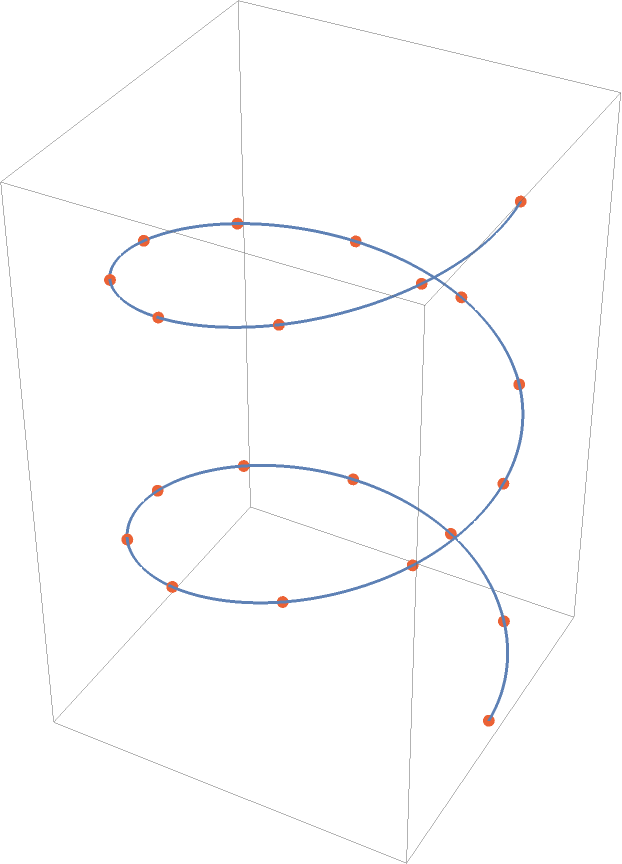 |
Show the interpolating cubic B-spline as a Tube:
| In[7]:= | ![Graphics3D[{{Directive[AbsoluteThickness[3], ColorData[97, 1]], Tube[ResourceFunction["CubicSplineCurve"][pts], 0.03]}, {Directive[
AbsolutePointSize[6], ColorData[97, 4]], Sphere[pts, 0.05]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/d48/d4868462-3a51-4922-a30e-dcd3b58d6943/4307ea97571a2ac3.png) |
| Out[7]= | 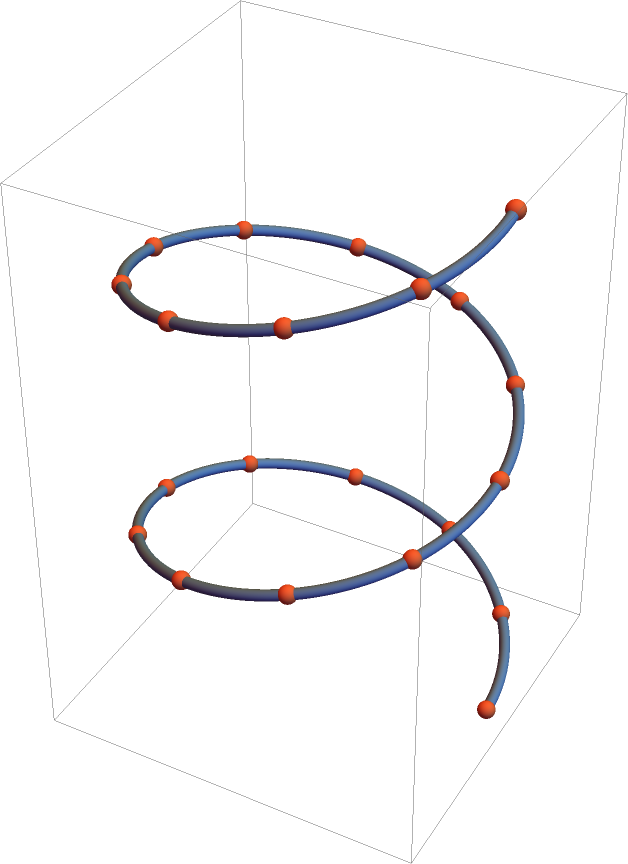 |
Use SplineClosed→True to interpolate a set of points with a closed B-spline:
| In[8]:= | ![pts = With[{n = 12}, Table[N[AngleVector[{1 + (-1)^i/4, 2 \[Pi] i/n}]], {i, 0, n}]];
Graphics[{{Directive[AbsoluteThickness[3], ColorData[97, 1]], ResourceFunction["CubicSplineCurve"][pts, SplineClosed -> True]}, {Directive[AbsolutePointSize[6], ColorData[97, 4]], Point[pts]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/d48/d4868462-3a51-4922-a30e-dcd3b58d6943/46dd8336cce93455.png) |
| Out[8]= | 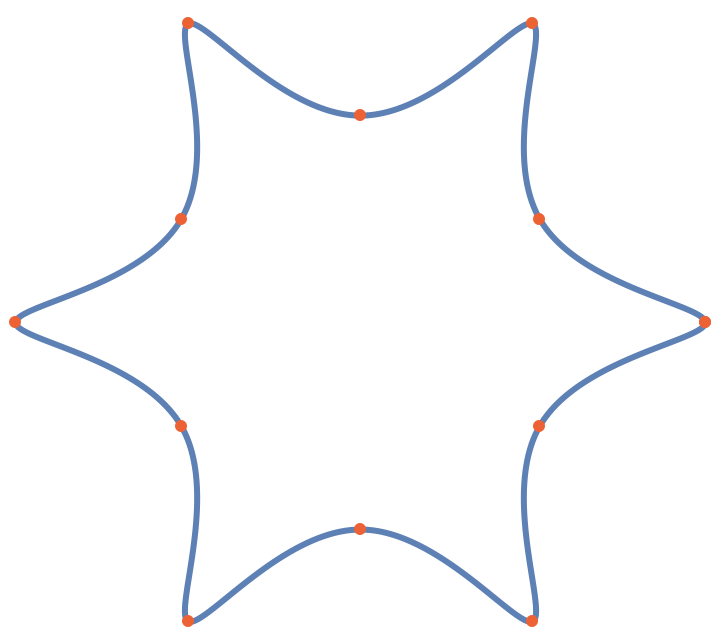 |
Convert the result of KnotData into a BSplineCurve:
| In[9]:= | ![pts = Transpose[
KnotData["FigureEight", "SpaceCurve"]["ValuesOnGrid"]] . DiagonalMatrix[{1, 1, 1/3}];
knot = ResourceFunction["CubicSplineCurve"][pts, SplineClosed -> True];
Graphics3D[{Directive[AbsoluteThickness[2], ColorData[97, 3]], knot}, Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/d48/d4868462-3a51-4922-a30e-dcd3b58d6943/2b94240dff3a2f24.png) |
| Out[9]= | 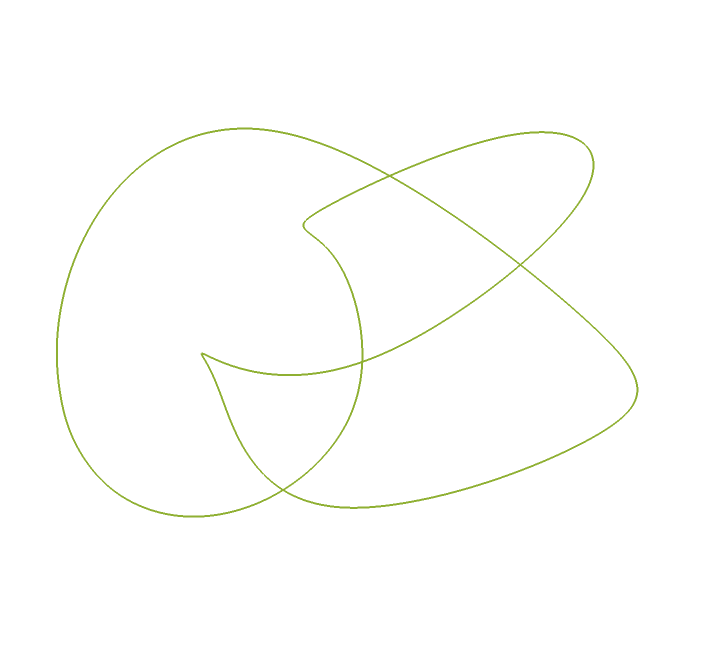 |
Visualize the knot as a Tube:
| In[10]:= |
| Out[10]= | 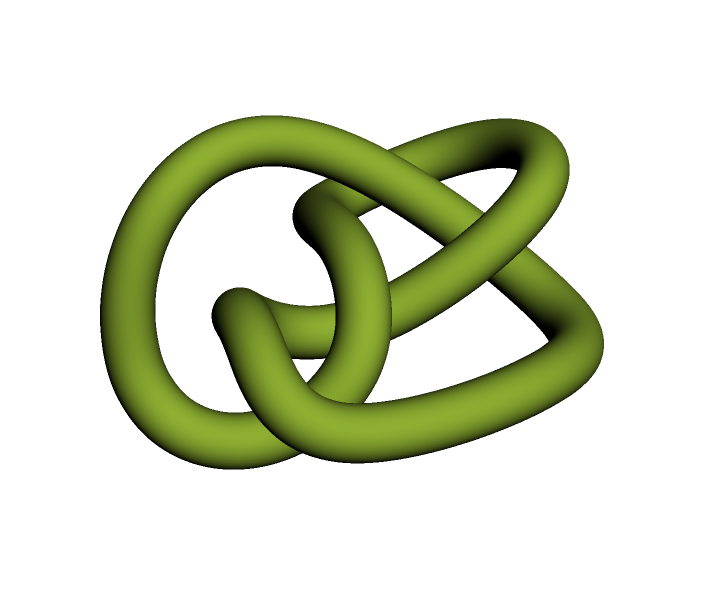 |
This work is licensed under a Creative Commons Attribution 4.0 International License