Basic Examples (3)
Count the number of solutions to a bivariate system:
Compare to the number of solutions produced by Solve:
Compare instead to the number of solutions produced by NSolve:
Scope (5)
Count the solutions to a trivariate system with two polynomials of degree 3 and one of degree 4:
Count the solutions to a larger system:
Count the solutions to an "offset" system, wherein the polynomials are set equal to nonzero constants:
Coefficients need not be rational:
This is somewhat faster than explicitly solving the system:
It is faster still to do the computation at modest finite precision:
Coefficients can be parameters, that is, unknown values:
We check that this is in fact the count for a specific set of parameter values:
An overdetermined system often will have no solutions:
A system of n polynomials in n variables might fail to have a finite solution set:
If we allow z to be a parameter then the solution count is finite:
Options (2)
This is a test system from an ISSAC 2001 conference paper:
It is quite slow to handle at exact precision:
It can be done quite efficiently at a working precision of 200 digits:
This is moreover several times faster than numerically solving the system at the same precision:
A more extreme example comes from a 2009 ISSAC conference paper:
NSolve on this example is 2-3 orders of magnitude slower:
Properties and Relations (3)
The Caprasse system has 32 distinct solutions:
A count by multiplicity shows a larger value:
If we slightly perturb the system then Solve will find 56 distinct solutions in agreement with CountPolynomialSolutions:
Possible Issues (4)
Inconsistent results can arise if the system (taken from this Mathematica.StackExchange post) has coefficients with low precision:
We can get a different count by raising the precision:
As is indicated in the StackExchange thread, there are further subtleties-- six of the eight solutions are quite large:
This is because the exact system from which this was taken lives on the "discriminant variety" for systems with the same polynomial structure but having generic coefficients. Had we an exact form for the coefficients, these six would not be present (they go to infinity as the coefficients approach the discriminant variety).
One can isolate to the two expected solutions with some amount of trial and error in setting the Tolerance option of GroebnerBasis:

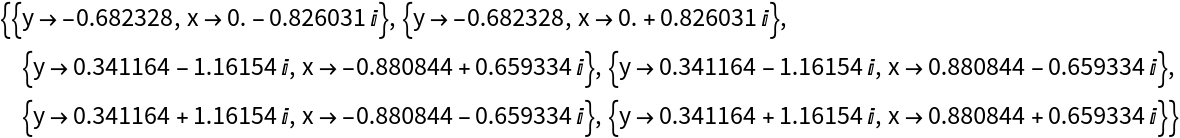
![polys = {x^3 + 5*x*z - 2*x*y - y^2 + z^3 - 3*y^2*z, y^3 + x^2*y - 7*x*y^2 + 3*x^2 - 5*x*y - 1, x*z^2 + 4*x*y*z + y^2*z - 2*z + x^2*y*z - 11};
ResourceFunction["CountPolynomialSolutions"][polys, {x, y, z}]](https://www.wolframcloud.com/obj/resourcesystem/images/0c6/0c61fa1d-ddc8-4bc7-bc5d-dc4d1cdd3b7f/1-0-1/1232bac7bd8d9101.png)
![polys = {a^5 + 30*a^3*b + 40*a^2*c + 89*a*b^2 + 88*b*c, a^6 + 55*a^4*b + 80*a^3*c + 439*a^2*b^2 + 688*a*b*c + 225*b^3 + 160*c^2, a^7 + 91*a^5*b + 140*a^4*c + 1519*a^3*b^2 + 2968*a^2*b*c + 3429*a*b^3 + 1120*a*c^2 + 3708*b^2*c};
ResourceFunction["CountPolynomialSolutions"][polys, Variables[polys]]](https://www.wolframcloud.com/obj/resourcesystem/images/0c6/0c61fa1d-ddc8-4bc7-bc5d-dc4d1cdd3b7f/1-0-1/4ce042e4e80dfc63.png)
![polys = {x0^2 + x1^2 + x2^2 - 1, x0*x3 + x1*x4 + x2*x5, x3^2 + x4^2 + x5^2 - 3/10, x3^2 + x4^2 - 2*x2*x4 + x2^2 + x5^2 + 2*x1*x5 + x1^2 - 1/4, x3^2 + Sqrt[3]*x2*x3 + 3/4*x2^2 + x4^2 - x2*x4 + 1/4*x2^2 + x5^2 - Sqrt[3]*x0*x5 + x1*x5 + 3/4*x0^2 - Sqrt[3]/2*x0*x1 + 1/4*x1^2 - 1/4, x3^2 - 2/3*Sqrt[6]*x1*x3 + Sqrt[3]/3*x2*x3 + 2/3*x1^2 - Sqrt[18]/9*x1*x2 + 1/12*x2^2 + x4^2 + 2/3*Sqrt[6]*x0*x4 - x2*x4 + 2/3*x0^2 - Sqrt[6]/3*x0*x2 + 1/4*x2^2 + x5^2 - Sqrt[3]/3*x0*x5 + x1*x5 + 1/12*x0^2 - Sqrt[3]/6*x0*x1 + 1/4*x1^2 - 1/4};
Timing[ResourceFunction["CountPolynomialSolutions"][
polys, {x0, x1, x2, x3, x4, x5}]]](https://www.wolframcloud.com/obj/resourcesystem/images/0c6/0c61fa1d-ddc8-4bc7-bc5d-dc4d1cdd3b7f/1-0-1/0a9a9d2cfb89c2f2.png)
![With[{a = 12, b = -Pi^2, c = E, d = I*Pi, e = EulerGamma},
polys = {a*x^2 - b*x*y^3, y^3 + c*x^2*y + d*x*y + e};
ns = NSolve[polys, {x, y}];
{ns, Length[ns]}]](https://www.wolframcloud.com/obj/resourcesystem/images/0c6/0c61fa1d-ddc8-4bc7-bc5d-dc4d1cdd3b7f/1-0-1/7ada821b63ab7010.png)

![polys = {x + x^2 + y - 2 x y - 3 x z^2, 7 + x^4 + x y^2 + y^4 + z^2, 7 - x - x^2 + 10 x^3 + 4 x^4 + x^7 - y - 19 x y + 5 x^2 y - 4 x^3 y - 3 x^5 y + 7 y^2 + 17 x y^2 - 4 x^2 y^2 + 2 x^4 y^2 + 2 x^5 y^2 - 3 x^2 y^3 + y^4 + x^2 y^4 + x^3 y^4 - y^5 - x y^5 + y^6 + 2 x y^6 - 14 y z - 2 x^4 y z - 3 x y^3 z - x^2 y^3 z - y^4 z + 2 x y^4 z - 2 y^5 z + 8 z^2 + 3 x z^2 - x^2 z^2 - 9 x^3 z^2 + x^4 z^2 - 4 x y z^2 - 4 x^2 y z^2 + y^2 z^2 + 3 x y^2 z^2 + y^4 z^2 + 3 x y^4 z^2 - 2 y z^3 + 3 x y^3 z^3 + z^4 + 3 x^2 z^4};
ResourceFunction["CountPolynomialSolutions"][polys, {x, y, z}]](https://www.wolframcloud.com/obj/resourcesystem/images/0c6/0c61fa1d-ddc8-4bc7-bc5d-dc4d1cdd3b7f/1-0-1/737a2143012f550b.png)
![g0 = -84 + 41*x + 23*y + 99*x^2*y^5 - 61*x^2*y^4 - 50*x^2*y^3 - 12*x^2*y^2 - 18*x^2*y - 26*x*y^7 - 62*x*y^6 + x*y^5 - 47*x*y^4 - 91*x*y^3 - 47*x*y^2 + 66*x^3*y - 55*x^7*y - 35*x^6*y^2 + 97*x^6*y + 79*x^5*y^3 + 56*x^5*y^2 + 49*x^5*y + 57*x^4*y^4 - 59*x^4*y^3 + 45*x^4*y^2 - 8*x^4*y + 92*x^3*y^5 + 77*x^3*y^2 + 54*x^3 + 53*y^6 + 31*x^2 - 90*y^7 - 58*y^8 - 85*x^8 - 37*x^7 - 86*y^2 + 50*x^6 + 83*y^3 + 63*x^5 + 94*y^4 - 93*x^4 - y^5 - 5*x^2*y^6 - 61*x*y + 43*x^3*y^4 - 62*x^3*y^3;
h0 = -76 - 53*x + 88*y + 66*x^2*y^5 - 29*x^2*y^4 - 91*x^2*y^3 - 53*x^2*y^2 - 19*x^2*y + 68*x*y^6 - 72*x*y^5 - 87*x*y^4 + 79*x*y^3 + 43*x*y^2 + 80*x^3*y - 50*x^6*y - 53*x^5*y^2 + 85*x^5*y + 78*x^4*y^3 + 17*x^4*y^2 + 72*x^4*y + 30*x^3*y^2 + 72*x^3 - 23*y^6 - 47*x^2 - 61*y^7 + 19*x^7 - 42*y^2 + 88*x^6 - 34*y^3 + 49*x^5 + 31*y^4 - 99*x^4 - 37*y^5 - 66*x*y - 85*x^3*y^4 - 86*x^3*y^3;
f0 = Expand[g0*h0];
polys = {f0, D[f0, x], D[f0, y]};
vars = Variables[polys];](https://www.wolframcloud.com/obj/resourcesystem/images/0c6/0c61fa1d-ddc8-4bc7-bc5d-dc4d1cdd3b7f/1-0-1/189abc3bd54dc68d.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/95ab119d-1885-4fea-9164-26c00a7783e6"]](https://www.wolframcloud.com/obj/resourcesystem/images/0c6/0c61fa1d-ddc8-4bc7-bc5d-dc4d1cdd3b7f/1-0-1/7e7194b2b7048117.png)
![polysCaprasse = {-2*x + 2*t*x*y - z + y^2*z, 2 + 4*x^2 - 10*t*y + 4*t*x^2*y - 10*y^2 + 2*t*y^3 + 4*x*z - x^3*z + 4*x*y^2*z, -x + t^2*x - 2*z + 2*t*y*z, 2 - 10*t^2 - 10*t*y + 2*t^3*y + 4*x*z + 4*t^2*x*z + 4*z^2 + 4*t*y*z^2 - x*z^3};
Length[Solve[polysCaprasse == 0]]](https://www.wolframcloud.com/obj/resourcesystem/images/0c6/0c61fa1d-ddc8-4bc7-bc5d-dc4d1cdd3b7f/1-0-1/3b63cc4b71c011ce.png)
![perturbpolysCaprasse = {-2*x + 2*t*x*y - (100001*z)/100000 + y^2*z, 2000001/1000000 + 4*x^2 - 10*t*y + 4*t*x^2*y - 10*y^2 + 2*t*y^3 + 4*x*z - x^3*z + 4*x*y^2*z, -x + t^2*x - 2*z + 2*t*y*z, 2 - 10*t^2 - 10*t*y + 2*t^3*y + 4*x*z + 4*t^2*x*z + 4*z^2 + 4*t*y*z^2 - x*z^3};
{Length[Solve[perturbpolysCaprasse == 0]], ResourceFunction["CountPolynomialSolutions"][perturbpolysCaprasse]}](https://www.wolframcloud.com/obj/resourcesystem/images/0c6/0c61fa1d-ddc8-4bc7-bc5d-dc4d1cdd3b7f/1-0-1/2d22ad4fbb14fead.png)
![polys = {-1 + c1^2 + s1^2, -1 + c2^2 + s2^2, -1 + c3^2 + s3^2, -1 + (-0.70873 c1 + c2 - 0.70548 s1) y11, -1 + (-0.916596 c2 + c3 + 0.399814 s2) y12, -1 + (c1 + 0.808085 c3 + 0.589066 s3) y13, -1 + (c1 + 0.808085 c3 + 0.589066 s3) y21, (-0.70548 c1 + 0.70873 s1 + s2) y11 - (-0.589066 c3 + s1 + 0.808085 s3) y21, -1 + (-0.70873 c1 + c2 - 0.70548 s1) y22, (0.399814 c2 + 0.916596 s2 + s3) y12 - (-0.70548 c1 + 0.70873 s1 + s2) y22, -1 + (-0.916596 c2 + c3 + 0.399814 s2) y23, (0.589066 c3 - s1 - 0.808085 s3) y13 - (0.399814 c2 + 0.916596 s2 + s3) y23};
ResourceFunction["CountPolynomialSolutions"][polys, Variables[polys]]](https://www.wolframcloud.com/obj/resourcesystem/images/0c6/0c61fa1d-ddc8-4bc7-bc5d-dc4d1cdd3b7f/1-0-1/1052e328111d013c.png)
![SetOptions[GroebnerBasis, Tolerance -> 10^(-4)];
ResourceFunction["CountPolynomialSolutions"][
SetPrecision[polys, 200]]
SetOptions[GroebnerBasis, Tolerance -> 0];](https://www.wolframcloud.com/obj/resourcesystem/images/0c6/0c61fa1d-ddc8-4bc7-bc5d-dc4d1cdd3b7f/1-0-1/284fba708bb92d4d.png)