Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find the partition of a triangle into cevian triangles with congruent incircles
ResourceFunction["CongruentIncirclePartition"][{p1,p2,p3},n] partition a triangle defined by vertices p1,p2 and p3 into cevian triangles that share vertex p1 and the same inradius. |
| "Partitions" | The number n of cevian triangles |
| "Inradius" | The radius of the incircle in each cevian triangle |
| "Incircles" | The congruent incircles |
| "CevianEndpoints" | The vertices of each cevian triangle other than p1 on segment p2p3 |
| "CevianTriangles" | Cevian triangles from by p1and two adjacent in "CevianEndpoints" |
Return an association containing the information of a partition of a given triangle into subtriangles sharing incircles of same size:
| In[1]:= |
| Out[2]= |  |
Find a cevian partition of a given triangle into 7 triangle with incircles of same size:
| In[3]:= |
| In[4]:= |
| In[5]:= | ![res = ResourceFunction["CongruentIncirclePartition"][v, 7];
Graphics[{
{Transparent, EdgeForm[{RGBColor["#ffc300"], Thick}], res["CevianTriangles"]},
{Transparent, EdgeForm[{RGBColor["#000814"], Thick}], Triangle[v]},
{Thick, RGBColor["#003566"], res["Incircles"]},
MapThread[label[#1, #2] &, {{"A", "B", "C"}, Point /@ v}]
}, ImageSize -> 400]](https://www.wolframcloud.com/obj/resourcesystem/images/68f/68f66002-b176-4651-8fc2-9fa2cffcd087/66d155fb6368870e.png) |
| Out[6]= | 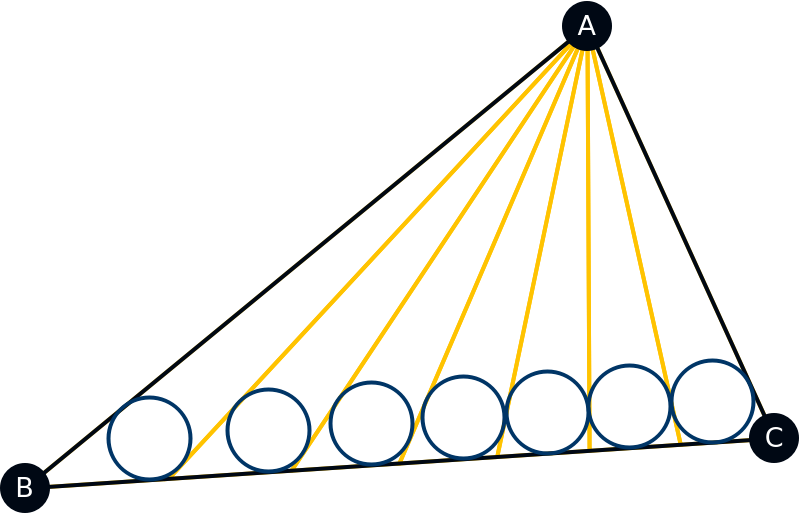 |
For each orientation, find a 4-part cevian partition:
| In[7]:= |
| In[8]:= |
| In[9]:= | ![GraphicsRow[Table[
res = ResourceFunction["CongruentIncirclePartition"][ele, 4];
Graphics[{
{Transparent, EdgeForm[{RGBColor["#ffc300"], Thick}], res["CevianTriangles"]},
{Transparent, EdgeForm[{RGBColor["#000814"], Thick}], Triangle[v]},
{Thick, RGBColor["#003566"], res["Incircles"]},
MapThread[label[#1, #2] &, {{"A", "B", "C"}, Point /@ v}]
}], {ele, rv}], ImageSize -> 870, Dividers -> All, ImagePadding -> 4]](https://www.wolframcloud.com/obj/resourcesystem/images/68f/68f66002-b176-4651-8fc2-9fa2cffcd087/19096e185b05a602.png) |
| Out[9]= | 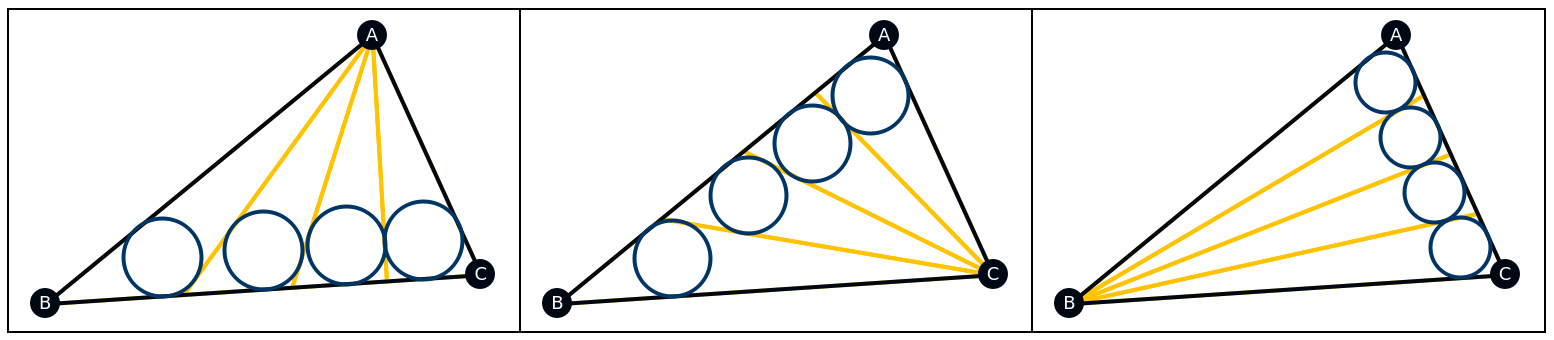 |
Certain triangles with integral sides also have integral inradii in a cevian triangle partition:
| In[10]:= |
| In[11]:= |
| Out[11]= |
| In[12]:= |
| In[13]:= |
| Out[13]= |
The number of partition must be at least 2. Otherwise the function returns unevaluated:
| In[14]:= |
| Out[14]= |
| In[15]:= |
| Out[15]= |  |
Degenerate triangles are not supported. The function returns unevaluated:
| In[16]:= |
| Out[16]= |
Perturb one vertex to create a non-degenerate case:
| In[17]:= |
| Out[17]= |  |
Coordinates must be real numeric values. Otherwise the function returns unevaluated:
| In[18]:= |
| Out[18]= |
Given an arbitrary triangle, let n-1 cevians be drawn from one of its vertices so all of the n triangles so determined have equal incircles. Then the incircles determined by spanning 2, 3,…, n-1 adjacent triangles are also equal (Wells 1991, p. 67). For instance, a spanning set of size 2:
| In[19]:= |
Check the inradii:
| In[20]:= |
| Out[21]= |
Visualize the cevian triangles and the incircles:
| In[22]:= |
| In[23]:= | ![GraphicsGrid[Partition[#, 3] &@Table[
Graphics[{
{LightGray, Line[{vert[[1]], #}] & /@ eps},
{Transparent, EdgeForm[{RGBColor["#ffc300"], Thick}], tri},
{Transparent, EdgeForm[{RGBColor["#000814"], Thick}], Triangle[vert]},
{Thick, RGBColor["#003566"], TriangleConstruct[tri, "Incircle"]},
MapThread[label[#1, #2] &, {{"A", "B", "C"}, Point /@ vert}]
}], {tri, gapTri}], ImageSize -> 780, Dividers -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/68f/68f66002-b176-4651-8fc2-9fa2cffcd087/5fafe41a5fbb7e8f.png) |
| Out[23]= | 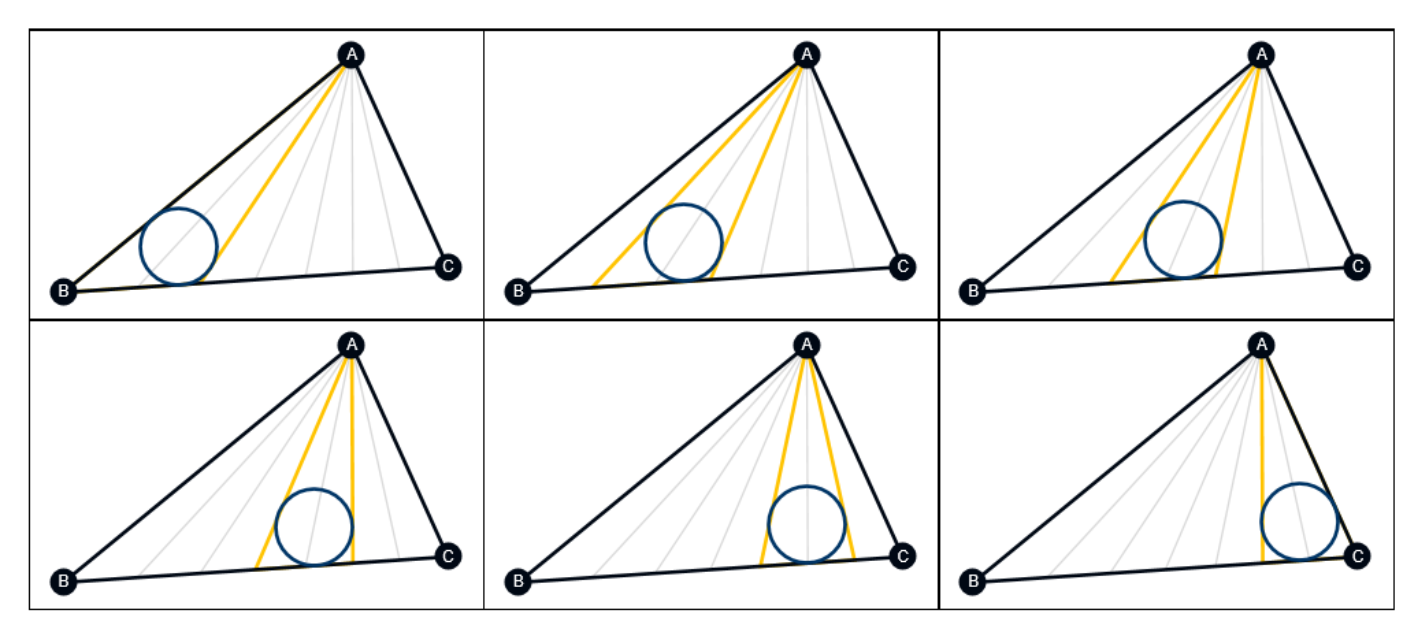 |
Show the same result for spanning 3 adjacent intervals:
| In[24]:= |
| Out[25]= |
| In[26]:= | ![GraphicsGrid[Partition[#, UpTo@3] &@Table[
Graphics[{
{LightGray, Line[{vert[[1]], #}] & /@ eps},
{Transparent, EdgeForm[{RGBColor["#ffc300"], Thick}], tri},
{Transparent, EdgeForm[{RGBColor["#000814"], Thick}], Triangle[vert]},
{Thick, RGBColor["#003566"], TriangleConstruct[tri, "Incircle"]},
MapThread[label[#1, #2] &, {{"A", "B", "C"}, Point /@ vert}]
}], {tri, gapTri}], ImageSize -> 780, Dividers -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/68f/68f66002-b176-4651-8fc2-9fa2cffcd087/302d2963ef3e44e2.png) |
| Out[26]= | 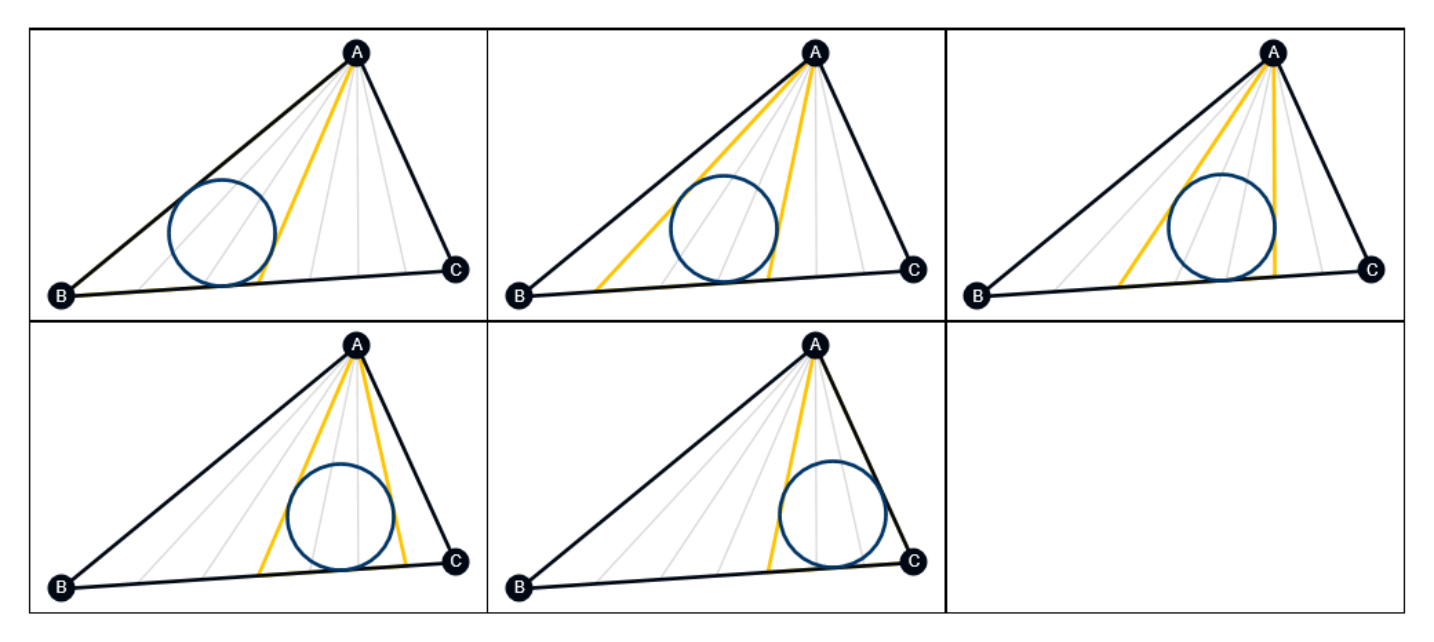 |
The observation follows this general argument: in triangle TSR if two cevian triangles TSU and TVR have the same inradius, so do triangles TSV and TUR:
| In[27]:= | ![gs = GeometricScene[{\[FormalT] -> {1.3, 1.5}, \[FormalS] -> {0, 0}, \[FormalU], \[FormalV], \[FormalR] -> {2, 0}},
{
Line[{\[FormalS], \[FormalU], \[FormalV], \[FormalR]}],
Triangle[{\[FormalT], \[FormalS], \[FormalR]}],
EuclideanDistance[\[FormalS], \[FormalU]] == 0.7,
TriangleMeasurement[Triangle@{\[FormalT], \[FormalS], \[FormalU]},
"Inradius"] == TriangleMeasurement[Triangle@{\[FormalT], \[FormalV], \[FormalR]},
"Inradius"]
}];
rs = RandomInstance[gs]](https://www.wolframcloud.com/obj/resourcesystem/images/68f/68f66002-b176-4651-8fc2-9fa2cffcd087/4529fb47ba64fcca.png) |
| Out[28]= | 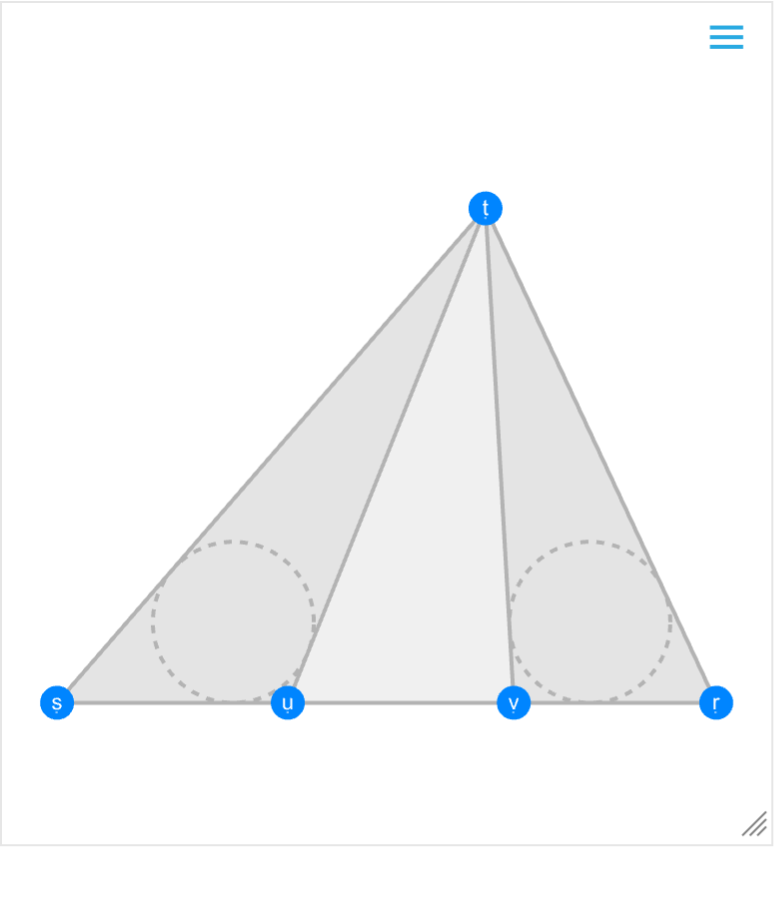 |
Visually verify the argument:
| In[29]:= | ![vFun[u_?NumericQ] := vLoc /. FindRoot[
TriangleMeasurement[{{1.3, 1.5}, {u, 0}, {0, 0}}, "Inradius"] ==
TriangleMeasurement[{{1.3, 1.5}, {vLoc, 0}, {2, 0}}, "Inradius"],
{vLoc, 2 - u}]](https://www.wolframcloud.com/obj/resourcesystem/images/68f/68f66002-b176-4651-8fc2-9fa2cffcd087/0608d1025f4792c9.png) |
| In[30]:= |
| In[31]:= | ![GraphicsRow[{
Plot[TriangleMeasurement[{{1.3, 1.5}, {intr[u], 0}, {0, 0}}, "Inradius"], {u, 0.2, 1.8},
PlotLabel -> "Inradius of TSV vs dist(SU)", AxesLabel -> {"dist(SU)", "Inradius"}],
Plot[TriangleMeasurement[{{1.3, 1.5}, {u, 0}, {2, 0}}, "Inradius"], {u, 0.2, 1.8},
PlotLabel -> "Inradius of TUR vs dist(SU)", AxesLabel -> {"dist(SU)", "Inradius"}]
}, ImageSize -> 720]](https://www.wolframcloud.com/obj/resourcesystem/images/68f/68f66002-b176-4651-8fc2-9fa2cffcd087/1fd5c53b0f72b0b6.png) |
| Out[31]= | 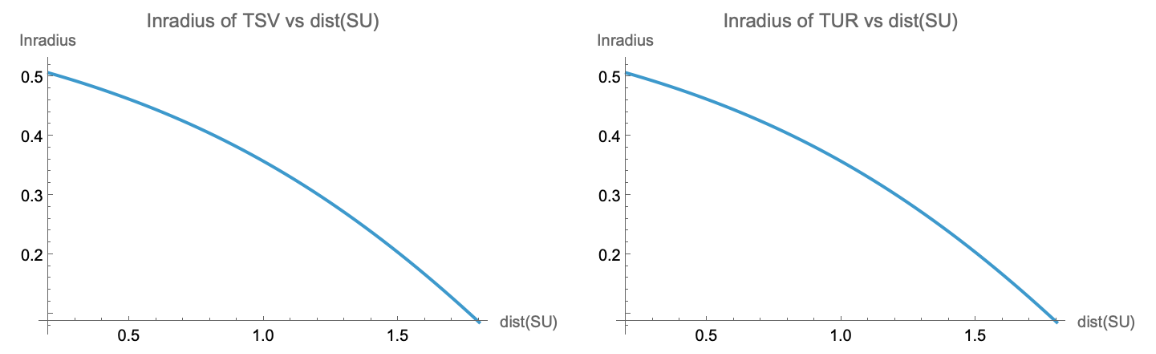 |
Wolfram Language 14.0 (January 2024) or above
This work is licensed under a Creative Commons Attribution 4.0 International License