Basic Examples (4)
Start with a categorical distribution:
Condition that distribution on the first dimension taking on a value of "A":
Find the probabilities from that categorical distribution conditioned on the second dimension taking on a value of "E":
Use a list of patterns instead of rules to impose the same condition as above:
Scope (3)
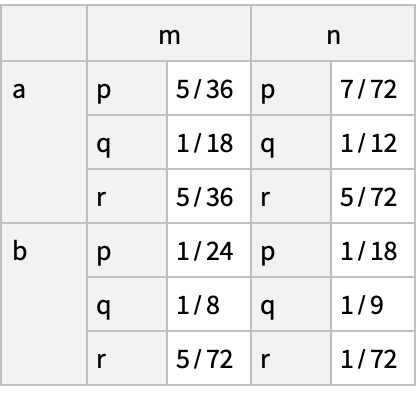
Patterns used in the conditions can be complex:
The first category must be a letter in the word "ABLE":
A CategoricalDistribution of arbitrary dimension works with the function:
The function works with univariate categorical distributions returning a CategoricalDistribution with potentially fewer categories:
Options (2)
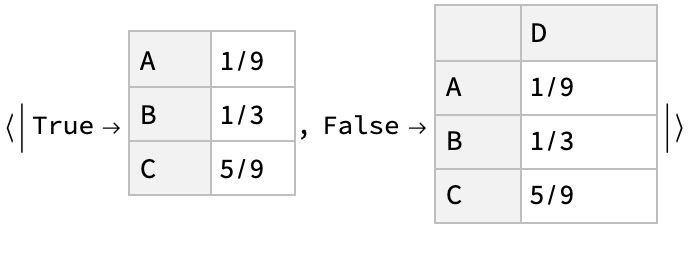
The value of the "FlattenUnivariate" option (True by default) determines whether the result of a univariate ConditionalCategoricalDistribution has its categories described without a List wrapper:
Setting the "Marginalize" option to False preserves the dimensionality of the original distribution:
Applications (2)
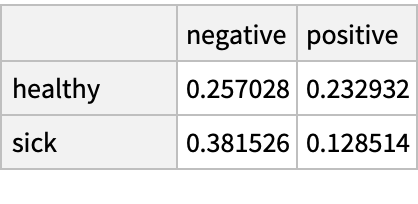
Here is the joint distribution of persons in group A or B who have or do not have some disease, and to whom a test classifies as negative or positive for the disease. Find the joint distribution of persons in group A with respect to disease and test result:
Find the probability that a person in group A who tests positive is actually sick:
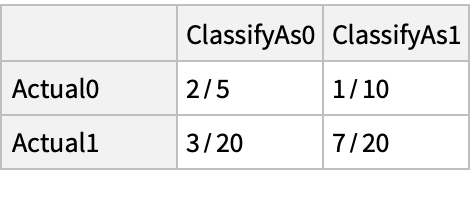
Compute the fractions of true positives (sensitivity), true negatives (specificity) and false positives (1-specificity) for a mixture of categorical distributions:
Neat Examples (4)
The following application comes from the field of causal inference, which is sometimes referred to as "do-calculus". Assume the joint probability distribution of the size of a kidney stone, the treatment one receives for it and how the outcome of that treatment is distributed as set forth below:
Compute the probability of a good outcome conditioned on the treatment. It will appear that B has better outcomes than A:
Now synthesize a randomized controlled trial and derive the interventional distribution when one forces the treatment to be "A" by computing a MixtureCategoricalDistribution over stone size in which the components are the conditional categorical distributions based on the stone size and the treatment being A:
Do exactly the same thing but force the treatment to be "B":
Although the observational distribution might suggest treatment B is superior, in fact, treatment A is superior and the observational distribution is distorted by the fact that small kidney stones, which generally have better outcomes, are more frequently treated with treatment B.
![Information[
Echo[ResourceFunction[
"ConditionalCategoricalDistribution"][{1 -> x_String /; StringContainsQ["ABLE", x]}, cd]], "Probabilities"]](https://www.wolframcloud.com/obj/resourcesystem/images/4bb/4bb76918-85f9-45d6-bc90-2d13c1b122dd/77716328a5d26fda.png)
![cd6 = CategoricalDistribution[{CharacterRange["a", "f"], CharacterRange["g", "k"], CharacterRange["l", "o"], CharacterRange["p", "r"], CharacterRange["s", "t"], CharacterRange["u", "z"]}, RandomInteger[{0, 10}, {6, 5, 4, 3, 2, 6}]]](https://www.wolframcloud.com/obj/resourcesystem/images/4bb/4bb76918-85f9-45d6-bc90-2d13c1b122dd/5861d52222a13ded.png)
![Information[
ResourceFunction[
"ConditionalCategoricalDistribution"][{1 -> "a" | "b", 2 -> "j", 5 -> "t", 3 -> "m" | "n", 6 -> "z"}, cd6], "ProbabilityTable"]](https://www.wolframcloud.com/obj/resourcesystem/images/4bb/4bb76918-85f9-45d6-bc90-2d13c1b122dd/78ac818dd68ad3e5.png)
![Information[
Echo[ResourceFunction["ConditionalCategoricalDistribution"][
"A" | "B", CategoricalDistribution[{"A", "B", "C"}, {0.6, 0.3, 0.1}]]], "Probabilities"]](https://www.wolframcloud.com/obj/resourcesystem/images/4bb/4bb76918-85f9-45d6-bc90-2d13c1b122dd/1e55508b8007c7c2.png)
![AssociationMap[
Information[
ResourceFunction["ConditionalCategoricalDistribution"][{1 -> "B"}, cd, "FlattenUnivariate" -> #], "Probabilities"] &, {True, False}]](https://www.wolframcloud.com/obj/resourcesystem/images/4bb/4bb76918-85f9-45d6-bc90-2d13c1b122dd/36197b590f962ca6.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/47fe7db1-42ea-4503-9a67-e5fdd633ed99"]](https://www.wolframcloud.com/obj/resourcesystem/images/4bb/4bb76918-85f9-45d6-bc90-2d13c1b122dd/75669c9db3763f2e.png)

![mixed = ResourceFunction[
ResourceObject[<|"Name" -> "MixtureCategoricalDistribution", "ShortName" -> "MixtureCategoricalDistribution", "UUID" -> "560477fe-b58d-40e2-9fd8-a914de0cbec2", "ResourceType" -> "Function", "Version" -> None, "Description" -> "Creates a mixture distribution of CategoricalDistributions but outputs it as a new CategoricalDistribution", "SymbolName" -> "FunctionRepository`$560477feb58d40e29fd8a914de0cbec2`MixtureCategoricalDistribution", "FunctionLocation" -> CloudObject[
"https://www.wolframcloud.com/obj/schandler/Resources/560/560477fe-b58d-40e2-9fd8-a914de0cbec2/download/DefinitionData"]|>, ResourceSystemBase -> Automatic]][
CategoricalDistribution[{"Small", "Big"}, {0.3, 0.7}], {CategoricalDistribution[{{"Actual0", "Actual1"}, {"ClassifyAs0", "ClassifyAs1"}}, {{80, 20}, {30, 70}}],
CategoricalDistribution[{{"Actual0", "Actual1"}, {"ClassifyAs0", "ClassifyAs1"}}, {{300, 80}, {50, 370}}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/4bb/4bb76918-85f9-45d6-bc90-2d13c1b122dd/66d72836bcdf8fa9.png)

![Map[(ResourceFunction["ConditionalCategoricalDistribution"][{#}, mixed] &)/*(Through[{tp, tn, fp}[#]] &), {"Small", "Big"}]](https://www.wolframcloud.com/obj/resourcesystem/images/4bb/4bb76918-85f9-45d6-bc90-2d13c1b122dd/5501b23dcc2a6792.png)
![mixed = ResourceFunction[
ResourceObject[<|"Name" -> "MixtureCategoricalDistribution", "ShortName" -> "MixtureCategoricalDistribution", "UUID" -> "560477fe-b58d-40e2-9fd8-a914de0cbec2", "ResourceType" -> "Function", "Version" -> None, "Description" -> "Creates a mixture distribution of CategoricalDistributions but outputs it as a new CategoricalDistribution", "SymbolName" -> "FunctionRepository`$560477feb58d40e29fd8a914de0cbec2`MixtureCategoricalDistribution", "FunctionLocation" -> CloudObject[
"https://www.wolframcloud.com/obj/schandler/Resources/560/560477fe-b58d-40e2-9fd8-a914de0cbec2/download/DefinitionData"]|>, ResourceSystemBase -> Automatic]][
CategoricalDistribution[{"Small", "Big"}, {3/10, 7/10}], {CategoricalDistribution[{{"Actual0", "Actual1"}, {"ClassifyAs0", "ClassifyAs1"}}, {{2/5, 1/10}, {3/
20, 7/20}}],
CategoricalDistribution[{{"Actual0", "Actual1"}, {"ClassifyAs0", "ClassifyAs1"}}, {{3/2, 2/5}, {1/4, 37/20}}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/4bb/4bb76918-85f9-45d6-bc90-2d13c1b122dd/277d9afe7cdf7df7.png)

![Information[
Echo[ResourceFunction[
"ConditionalCategoricalDistribution"][{1 -> "Small"}, mixed]], "ProbabilityTable"]](https://www.wolframcloud.com/obj/resourcesystem/images/4bb/4bb76918-85f9-45d6-bc90-2d13c1b122dd/3164a7c1efd1ca02.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/40647d3b-f3e3-4ad7-be73-67c21d41bdbc"]](https://www.wolframcloud.com/obj/resourcesystem/images/4bb/4bb76918-85f9-45d6-bc90-2d13c1b122dd/545ced166d231926.png)
![AssociationMap[
treatment |-> Information[
MarginalDistribution[
ResourceFunction[
"ConditionalCategoricalDistribution"][{2 -> treatment}, kidneys], 2], "Probabilities"] // N, {"A", "B"}]](https://www.wolframcloud.com/obj/resourcesystem/images/4bb/4bb76918-85f9-45d6-bc90-2d13c1b122dd/50d708934aac5041.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/1d3c1a6a-d31d-4a7b-9a4e-436fb02d83cf"]](https://www.wolframcloud.com/obj/resourcesystem/images/4bb/4bb76918-85f9-45d6-bc90-2d13c1b122dd/1a9c294f26218992.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/7b3baaa2-1a96-428e-8618-58ad9a062229"]](https://www.wolframcloud.com/obj/resourcesystem/images/4bb/4bb76918-85f9-45d6-bc90-2d13c1b122dd/5567ae5b639aa297.png)