Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ComradeMatrix

Source Notebook

Generate the comrade matrix corresponding to an orthogonal polynomial series

Contributed by: Jan Mangaldan

ResourceFunction["ComradeMatrix"][cof,poly]

yields the comrade matrix corresponding to , where pi(x) is an orthogonal polynomial represented by poly and ci is the (i+1)th element of the list cof.

Details

A comrade matrix is an upper Hessenberg matrix whose characteristic polynomial is a scalar multiple of the sum .
The argument poly can be any of the following:
"ChebyshevFirst"Chebyshev polynomial of the first kind ChebyshevT[i,x]
"ChebyshevSecond"Chebyshev polynomial of the second kind ChebyshevU[i,x]
"Hermite"Hermite polynomial HermiteH[i,x]
"Laguerre"Laguerre polynomial LaguerreL[i,x]
"Legendre"Legendre polynomial LegendreP[i,x]
{"Gegenbauer",m}Gegenbauer polynomial GegenbauerC[i,m,z]
{"Laguerre",a}Jacobi polynomial JacobiP[i,a,b,x]
{"Jacobi",a,b}Jacobi polynomial JacobiP[i,a,b,x]
Strings in specifications like "Legendre" and {"Jacobi",a,b} can be replaced with the corresponding built-in symbols, as in LegendreP and {JacobiP,a,b}.
If poly is "ChebyshevFirst", the comrade matrix is also referred to as a colleague matrix.
The result of ResourceFunction["ComradeMatrix"] is a SparseArray.

Examples

Basic Examples (3) 

The comrade matrix of a Legendre series:

In[1]:=
ResourceFunction["ComradeMatrix"][{1/2, 1/3, 1/5, 1}, "Legendre"] // MatrixForm
Out[1]=

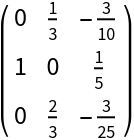
Compute its characteristic polynomial:

In[2]:=
CharacteristicPolynomial[%, x]
Out[2]=

The characteristic polynomial is a scalar multiple of the corresponding orthogonal polynomial series:

In[3]:=
Expand[(#/Coefficient[#, x, Exponent[#, x]]) &[{1/2, 1/3, 1/5, 1} . LegendreP[Range[0, 3], x]]]
Out[3]=

Scope (2) 

Comrade matrix of a Jacobi series with symbolic coefficients and parameters:

In[4]:=
ResourceFunction["ComradeMatrix"][ Array[C, 5, 0], {"Jacobi", \[Alpha], \[Beta]}] // MatrixForm
Out[4]=

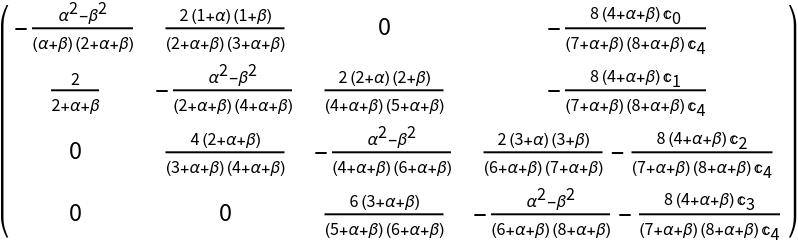
An equivalent specification:

In[5]:=
ResourceFunction["ComradeMatrix"][ Array[C, 5, 0], {JacobiP, \[Alpha], \[Beta]}] // MatrixForm
Out[5]=

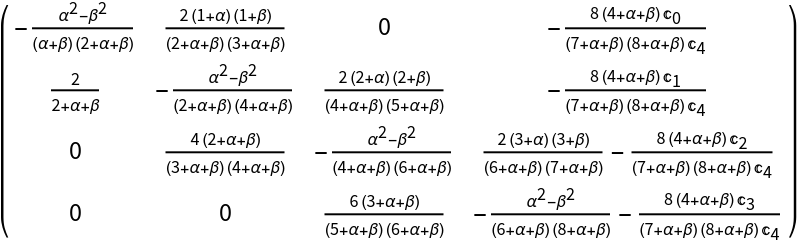
Generate a colleague matrix:

In[6]:=
ResourceFunction["ComradeMatrix"][Range[5], "ChebyshevFirst"] // MatrixForm
Out[6]=

Applications (2) 

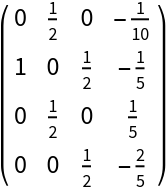
Use the comrade matrix with Eigenvalues to find the roots of a Chebyshev series of the second kind:

In[7]:=
Eigenvalues[ N[ResourceFunction["ComradeMatrix"][{-1/8, 1/4, -1/2, 1}, ChebyshevU]]]
Out[7]=

Compare with the result of using NSolve and the resource function OrthogonalPolynomialSum:

In[8]:=
x /. NSolve[ ResourceFunction["OrthogonalPolynomialSum"][{-1/8, 1/4, -1/2, 1}, ChebyshevU, x] == 0, x]
Out[8]=

Version History

  • 1.0.0 – 05 April 2021

Source Metadata

  • Citation:
    • Barnett S., "A companion matrix analogue for orthogonal polynomials." Linear Algebra and its Applications, vol. 12, no. 3, 197–202, 1975. DOI: 10.1016/0024-3795(75)90041-5
    • Barnett S., "Some applications of the comrade matrix." International Journal of Control, vol. 21, no. 5, 849–855, 1975. DOI: 10.1080/00207177508922039
    • Day D., Romero L., "Roots of Polynomials Expressed in Terms of Orthogonal Polynomials." SIAM Journal on Numerical Analysis, vol. 43, no. 5, 1969–1987, 2005. DOI: 10.1137/040609847
    • Good I.J., "The colleague matrix, a Chebyshev analogue of the companion matrix." The Quarterly Journal of Mathematics, vol. 12, no. 1, 61–68, 1961. DOI: 10.1093/qmath/12.1.61

Related Resources

License Information