Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Color the vertices in a graph with no adjacent vertices sharing a color
ResourceFunction["ColorGraphVertices"][graph] colors the vertices of graph with no adjacent vertices having the same color. | |
ResourceFunction["ColorGraphVertices"][graph, colors] uses colors from the color list colors. |
Color the vertices of the Petersen graph:
| In[1]:= |
| Out[1]= | 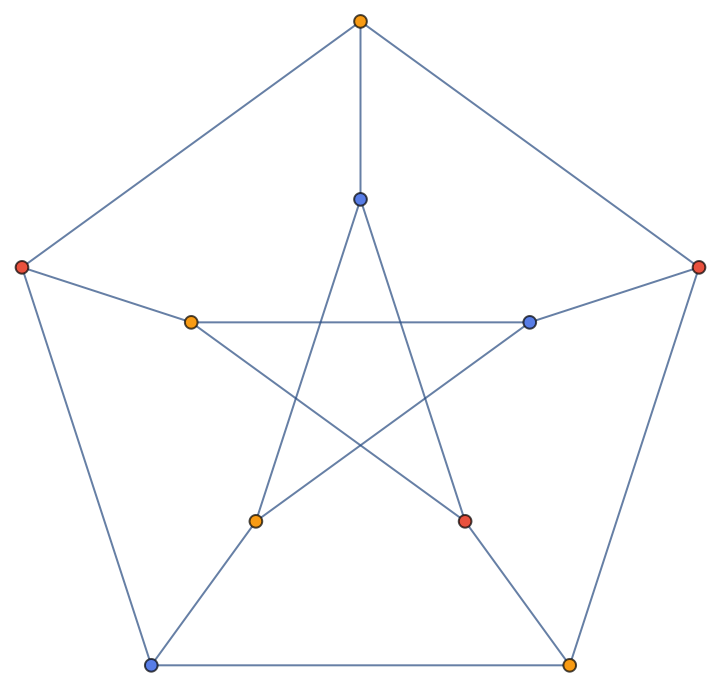 |
Color the vertices of the Petersen graph with color list 105:
| In[2]:= |
| Out[2]= | 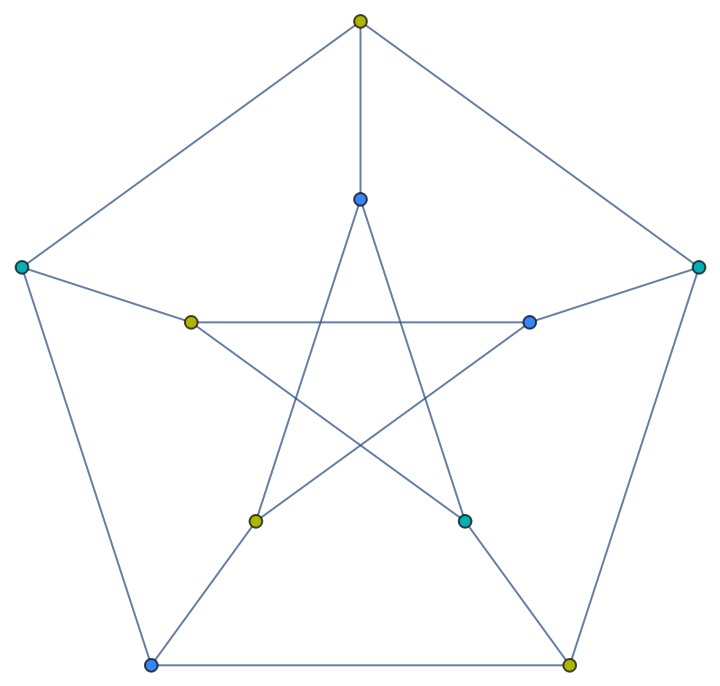 |
Color the vertices of the Petersen graph with a random sample of crayola colors:
| In[3]:= |
| Out[3]= | 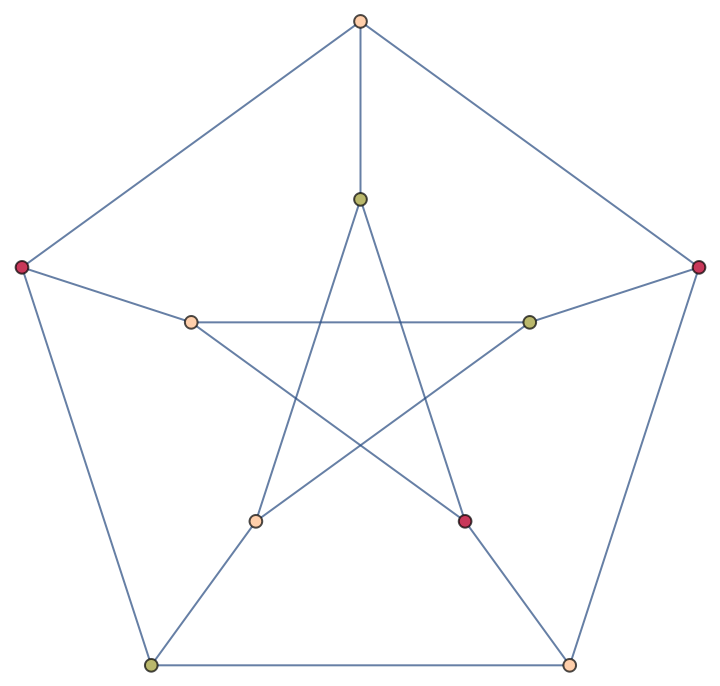 |
Color the vertices of the Pappus graph:
| In[4]:= |
| Out[4]= | 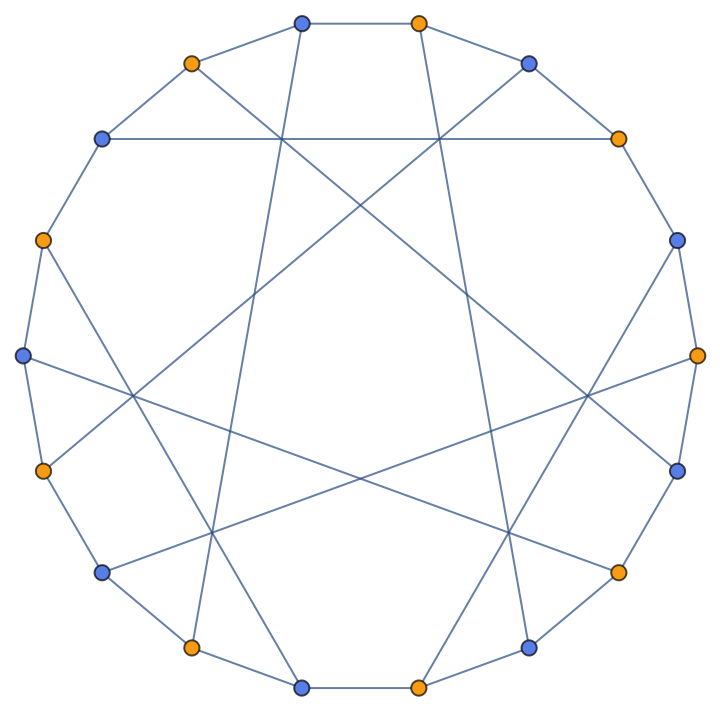 |
Use ColorGraphVertices to color the vertices, or nodes of a graph or network, respectively:
| In[6]:= |
| Out[6]= | 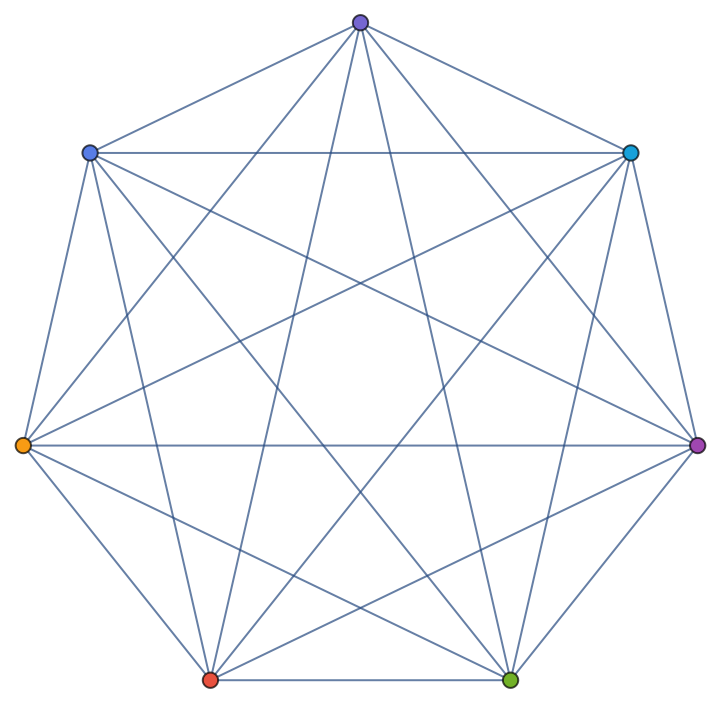 |
One can also color the edges:
| In[7]:= |
| Out[7]= | 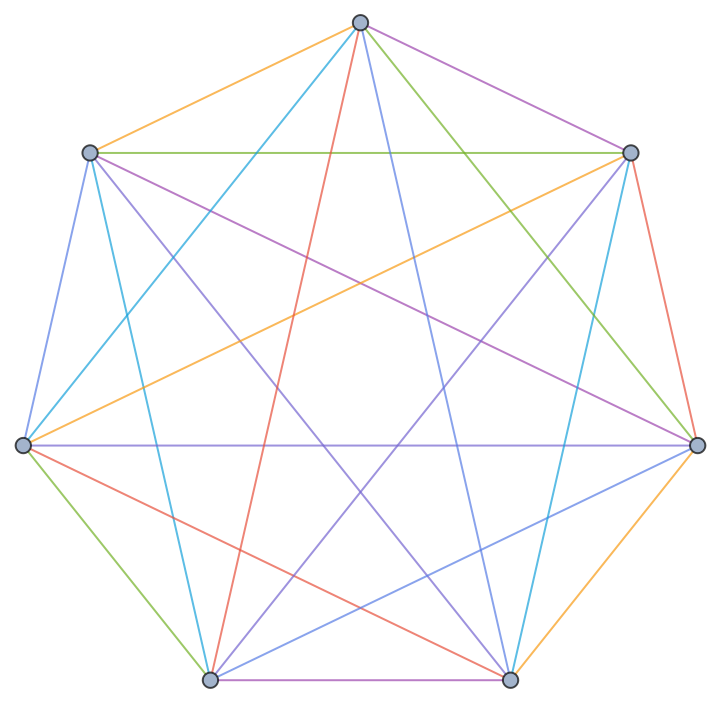 |
The number of colors needed for the vertices is given by VertexChromaticNumber:
| In[8]:= |
| Out[8]= |
Verify the cases with FindVertexColoring:
| In[9]:= |
| Out[9]= |
Color the vertices of the skeleton of the Császár polyhedron:
| In[10]:= |
| Out[10]= | 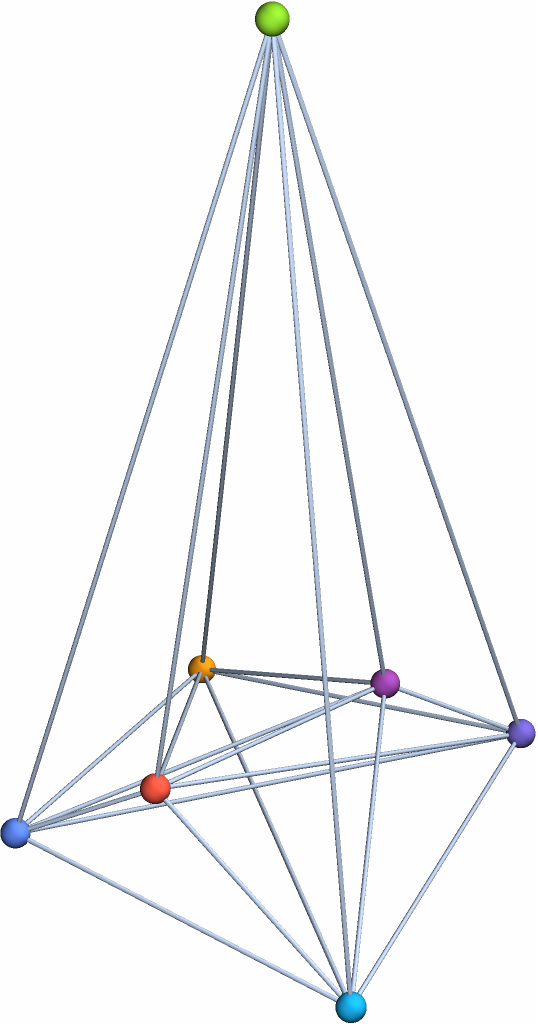 |
Make a large random graph and color the vertices:
| In[11]:= |
| Out[11]= | 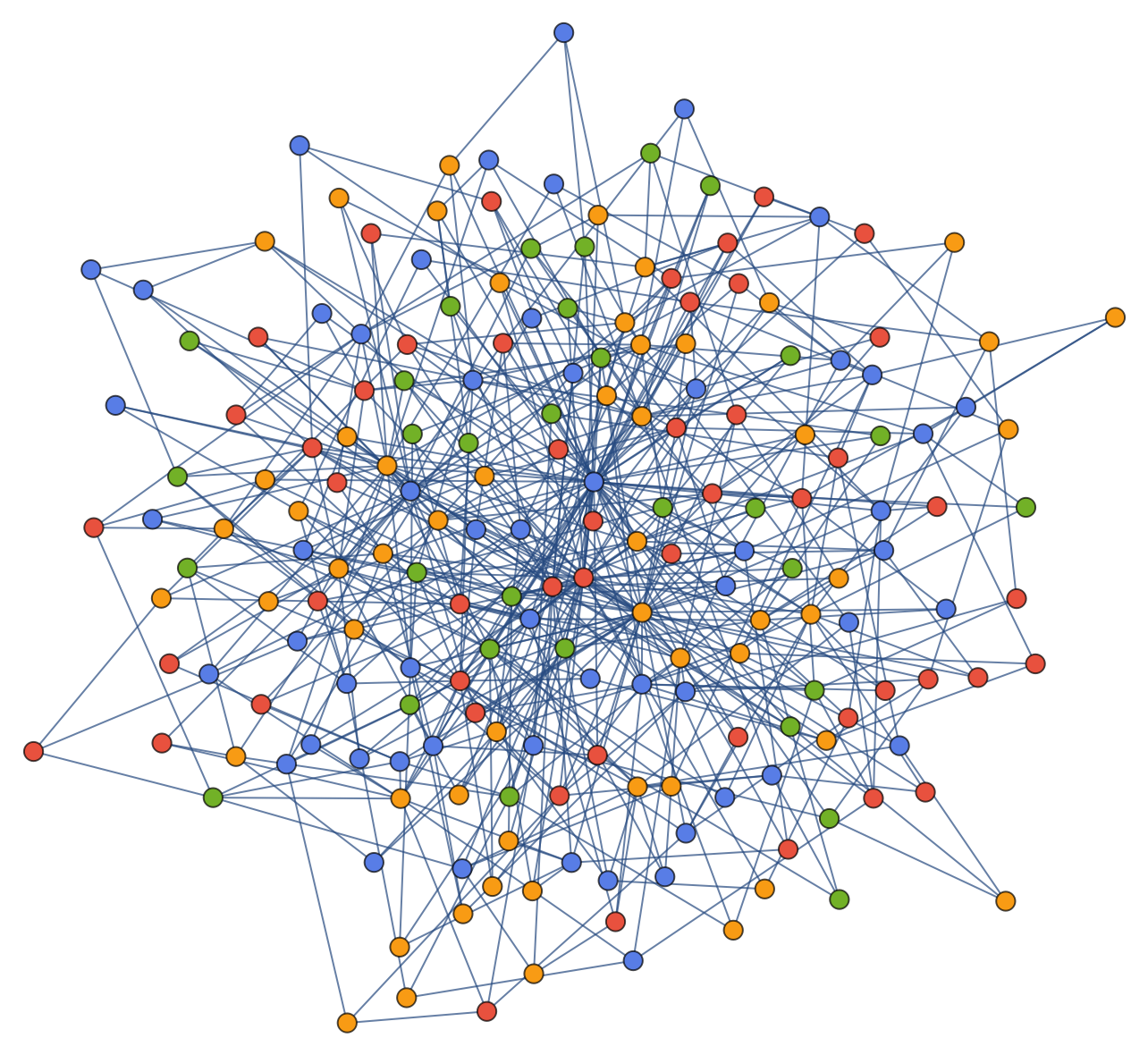 |
Make a 3D buckyball graph with colors:
| In[12]:= |
| Out[12]= | 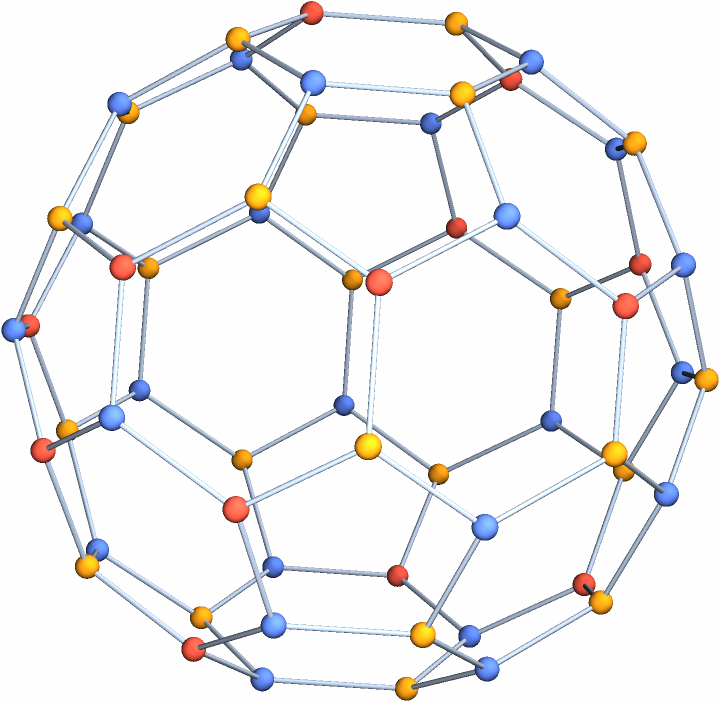 |
Wolfram Language 12.3 (May 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License