Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ColorFunctionRipple

Source Notebook

Give a color function a periodic perturbation

Contributed by: Mark Greenberg

ResourceFunction["ColorFunctionRipple"][cf]

introduces periodic perturbations to the color function cf.

Details and Options

In ResourceFunction["ColorFunctionRipple"][cf], cf may have a head of Function, ColorDataFunction or String.
When cf is a string, it should be the name of a built-in color scheme.
ResourceFunction["ColorFunctionRipple"] can take the following options:
"Profile""Waves"the shape of the perturbation
"Frequency"1how often the perturbations occur
Possible settings for the "Profile" option include the following:
"Waves"
"Layers"
"Crenels"
"Gullets"
"Hills"
"Troughs"

Examples

Basic Examples (1) 

Show a rippled gradient:

In[1]:=
LinearGradientImage[ ResourceFunction["ColorFunctionRipple"]["SunsetColors"], {600, 40}]
Out[1]=

Scope (2) 

Modify a color gradient represented as a pure function:

In[2]:=
LinearGradientImage[ ResourceFunction["ColorFunctionRipple"][ RGBColor[#, 1 - #, 1] &], {600, 40}]
Out[2]=

Modify a color gradient from the WFR:

In[3]:=
LinearGradientImage[ ResourceFunction[ "ColorFunctionRipple"][(ResourceFunction["ViridisColor"][{"Plasma", "Reverse"}, #]) &], {600, 40}]
Out[3]=

Options (2) 

Profile (1) 

Select a profile shape that best suits your needs:

In[4]:=
Column[Table[ Graphics[{Raster[{Range[500]/500}, ColorFunction -> ResourceFunction["ColorFunctionRipple"]["StarryNightColors", "Profile" -> p]], Text[Style[p, 14], {480, .5}, {1, 0}]}, AspectRatio -> .08, PlotRangePadding -> .1, ImageSize -> 600], {p, {"Waves", "Crenels", "Hills", "Layers", "Troughs", "Gullets"}}], Spacings -> 0]
Out[4]=

Frequency (1) 

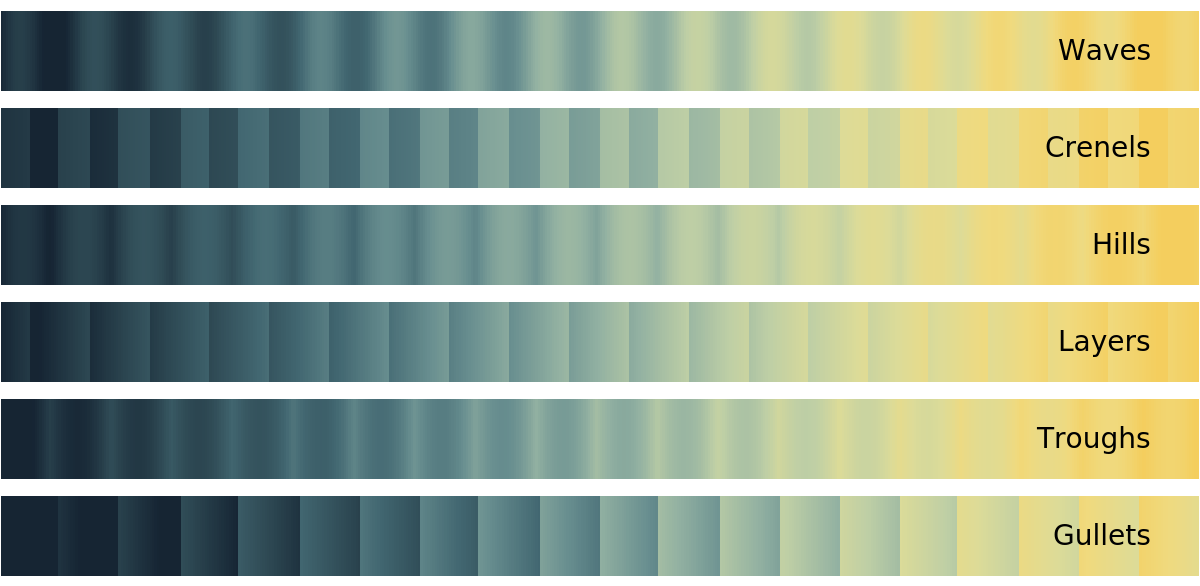Increase or decrease the number of ripples along the color function:

In[5]:=
Column[Table[ Graphics[{Raster[{Range[500]/500}, ColorFunction -> ResourceFunction["ColorFunctionRipple"]["CherryTones", "Frequency" -> p]], Text[Style[ToString[p], 14], {480, .5}, {1, 0}]}, AspectRatio -> .08, PlotRangePadding -> .1, ImageSize -> 600], {p, {.5, 1, 2, 4}}], Spacings -> 0]
Out[5]=

Applications (3) 

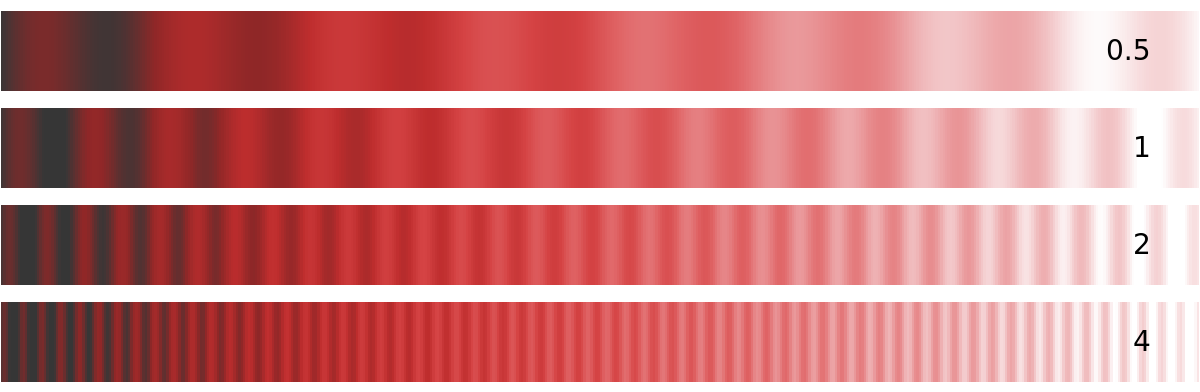Style a plot:

In[6]:=
cf = Blend[{{0, Darker[Blue]}, {1, White}}, #] &; Plot[Sin[x], {x, 0, 2 \[Pi]}, PlotStyle -> AbsoluteThickness[10], ColorFunction -> ResourceFunction["ColorFunctionRipple"][cf, "Profile" -> "Crenels"], AspectRatio -> .5, ImageSize -> 500]
Out[7]=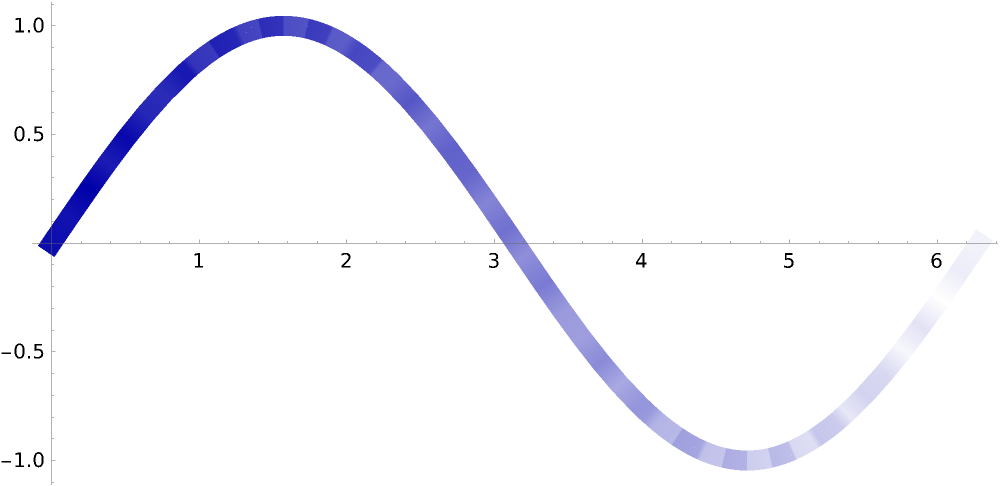

Style a 3D shape:

In[8]:=
ContourPlot3D[x^2 + y^2 + z^2, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, PlotPoints -> 100, MeshStyle -> None, Boxed -> False, ColorFunction -> ResourceFunction["ColorFunctionRipple"][Hue[#2, 2 #2, 2 #2] &], Axes -> None]
Out[23]=

Alter the surface colors of a relief plot:

In[24]:=
ReliefPlot[ Table[x + Sin[3 x + y^2], {x, -4, 4, 0.05}, {y, -4, 4, 0.05}], ColorFunction -> ResourceFunction["ColorFunctionRipple"]["SunsetColors", "Frequency" -> .5]]
Out[24]=

Possible Issues (2) 

ColorFunctionRipple currently does not support pure functions with named arguments:

In[25]:=
LinearGradientImage[ ResourceFunction["ColorFunctionRipple"][ Function[t, ColorData["M10DefaultDensityGradient"][t]]], {600, 40}]
Out[25]=

Use the gradient name directly instead:

In[26]:=
LinearGradientImage[ ResourceFunction["ColorFunctionRipple"][ "M10DefaultDensityGradient"], {600, 40}]
Out[26]=

Neat Examples (1) 

Create interesting visual effects:

In[27]:=
ParametricPlot3D[ Evaluate[ RotationTransform[ 2 \[Pi] v, {0, 0, 1}][.5^ v {Cos[2 \[Pi] u], 0, Sin[2 \[Pi] u]}] + .5^ v {Cos[2 \[Pi] v], Sin[2 \[Pi] v], -2.4}], {u, 0, 1}, {v, 0, 8}, PlotRange -> All, MaxRecursion -> 4, Mesh -> None, Boxed -> False, Axes -> False, PlotPoints -> 100, ColorFunction -> ResourceFunction["ColorFunctionRipple"][ColorData["Pastel"][#4] &, "Profile" -> "Hills"]]
Out[27]=

Publisher

Mark Greenberg

Version History

  • 1.0.0 – 20 January 2023

Related Resources

License Information