Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate the rooted binary tree using Colijn–Plazzotta bijection
ResourceFunction["ColijnPlazzottaTree"][n] generates the rooted binary tree with Colijn-Plazzotta bijection given rank n. | |
ResourceFunction["ColijnPlazzottaTree"][n,"SubtreeRanks"] returns the tuple from Colijn-Plazzotta subtrees. | |
ResourceFunction["ColijnPlazzottaTree"]["Reset"] clears the memory used for efficiency. |
Create the Colijn-Plazzotta tree with rank 20:
| In[1]:= |
| Out[1]= | 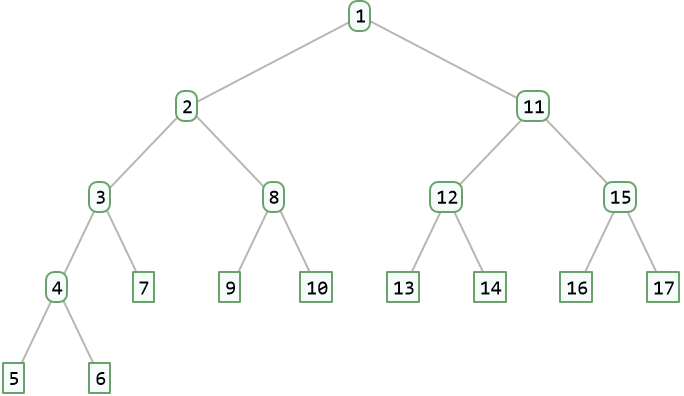 |
Tabulate the value of f(t) with the paired ranks from subtrees along with the associated binary tree and the number of leaves in each tree:
| In[2]:= | ![ResourceFunction["NiceGrid"][
Table[With[{t = ResourceFunction["ColijnPlazzottaTree"][k]}, {k, ResourceFunction["ColijnPlazzottaTree"][k, "SubtreeRanks"], t, TreeLeafCount[t]}], {k, 6}], {"f(t)", "(f(l(t)),f(r(t)))", "t", "# of leaves"}, ItemSize -> {{4, 11, 6, 8}}
]](https://www.wolframcloud.com/obj/resourcesystem/images/d6d/d6d22fb2-84fe-4b18-bab8-a10cdccb4445/0264d66326d78923.png) |
| Out[2]= | 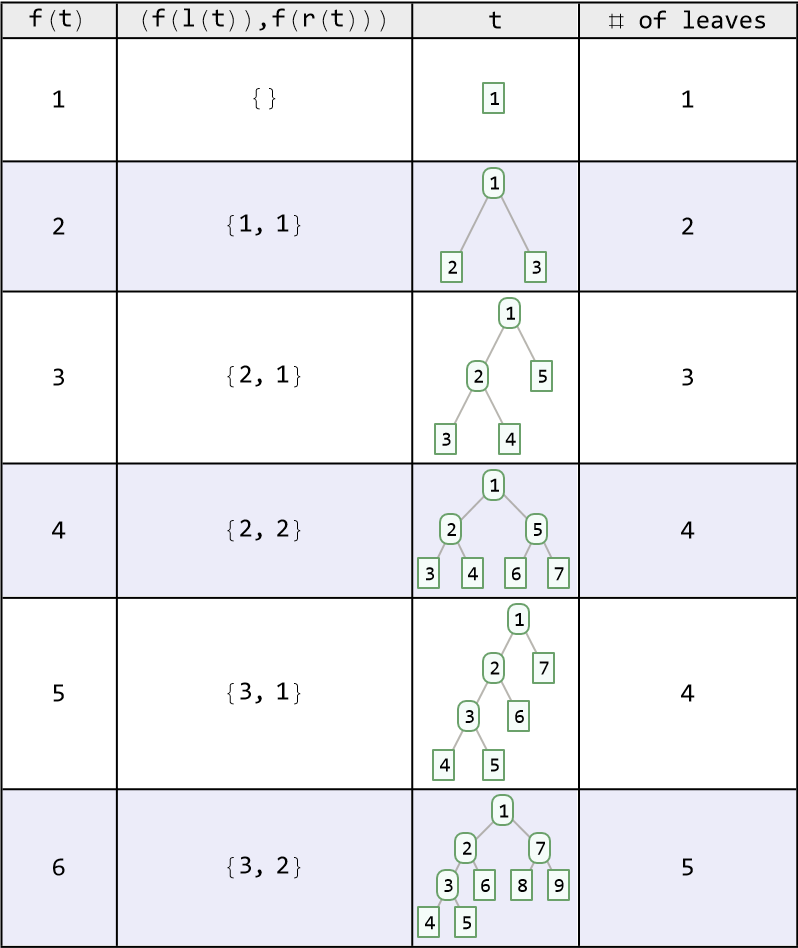 |
The sequence A357701 on OEIS lists the reading of the depth of each node in Colijn Plazzotta binary tree using pre-order depth first traversal. For instance, using n=6 in the example section on the OEIS page:
| In[3]:= |
| Out[3]= | 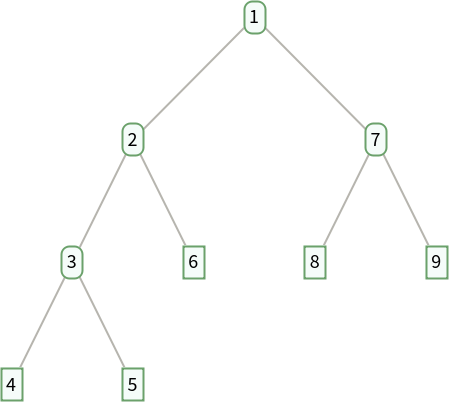 |
| In[4]:= |
| Out[4]= |
Retrieve the sequence from OEIS and highlight the matching values:
| In[5]:= | ![ResourceFunction["OEISSequence"][
"A357701"] /. {before___, s : PatternSequence[0, 1, 2, 3, 3, 2, 1, 2, 2], after___} :> {before, Sequence @@ ( Style[#, Red] & /@ {s}), after}](https://www.wolframcloud.com/obj/resourcesystem/images/d6d/d6d22fb2-84fe-4b18-bab8-a10cdccb4445/0197883a1a600b46.png) |
| Out[5]= |
The number of nodes grows very slowly with n:
| In[6]:= |
| Out[6]= | 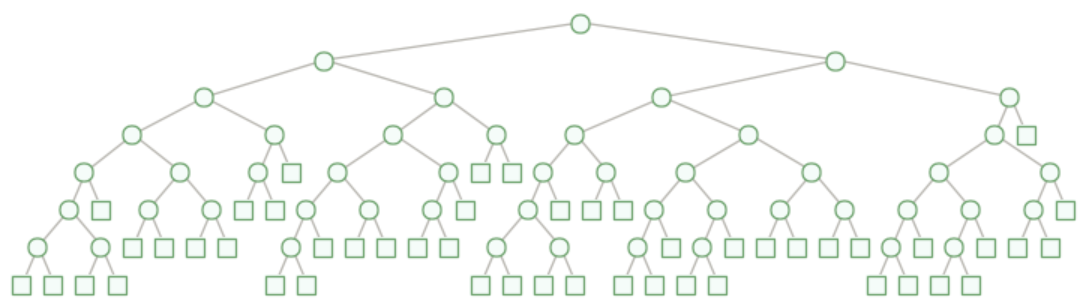 |
Convert the subtree ranks back to the input:
| In[7]:= |
| Out[7]= | 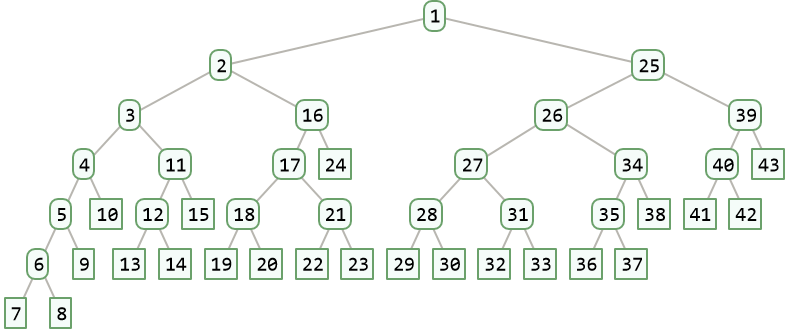 |
| In[8]:= |
| Out[9]= |
The input of ColijnPlazzottaTree must be a non-negative integer. Otherwise, the function returns unevaluated:
| In[10]:= |
| Out[10]= |
The leaf count for each Colijn-Plazzotta binary tree yields A064064 on OEIS:
| In[11]:= |
| Out[11]= |
The sequence has the following recurrence:
| In[12]:= |
| Out[12]= |
The dependence of the terms in the above recursive function call:
| In[13]:= |
| In[14]:= |
| Out[14]= |  |
Wolfram Language 14.0 (January 2024) or above
This work is licensed under a Creative Commons Attribution 4.0 International License