Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ClickRecurrenceMap2D

Source Notebook

Get the orbits of a planar map in an interactive way using a clickable panel

Contributed by: E. Chan-López, Erika Yuridia Flores Chan, Héctor Argote Morales & Víctor Castellanos

ResourceFunction["ClickRecurrenceMap2D"][map,depvars,trange,name]

gives the orbits corresponding to the recurrence equations represented by map, the dependent variables depvars and a pair trange containing the minimum and maximum number of iterations, with initial conditions determined by clicking within an interactive panel and an optional argument name used as a label for the iterated map in the interface.

Details and Options

The map must be a list of recurrence equations.
The depvars must be a list containing the dependent variables.
The trange must be a list containing the minimum and maximum number of iterations.
ResourceFunction["ClickRecurrenceMap2D"][map,depvars,trange] obtains initial condition data from points the user clicks and plots the corresponding orbits.
ResourceFunction["ClickRecurrenceMap2D"][map,depvars,trange] takes the same options as ListPlot.
ResourceFunction["ClickRecurrenceMap2D"][map,depvars,trange,name] name is an optional argument (default: "Unspecified Name") used to label the iterated map in the interface. If no name is provided, the default label "Unspecified Name" will be used.

Examples

Generate some orbits of the Gingerbreadman map:

In[1]:=
Gingerbreadman[{x_[n_], y_[n_]}] := {x[n + 1] == 1 - y[n] + Abs[x[n]], y[n + 1] == x[n]}
In[2]:=
X = {x[n], y[n]};

Visualize the orbit by clicking:

In[3]:=
ResourceFunction["ClickRecurrenceMap2D"][ Gingerbreadman[X], X, {1, 10000}, "Gingerbreadman map", {PlotStyle -> {{ AbsolutePointSize[1], GrayLevel[0]}}, AspectRatio -> 1, PlotHighlighting -> None}]
Out[3]=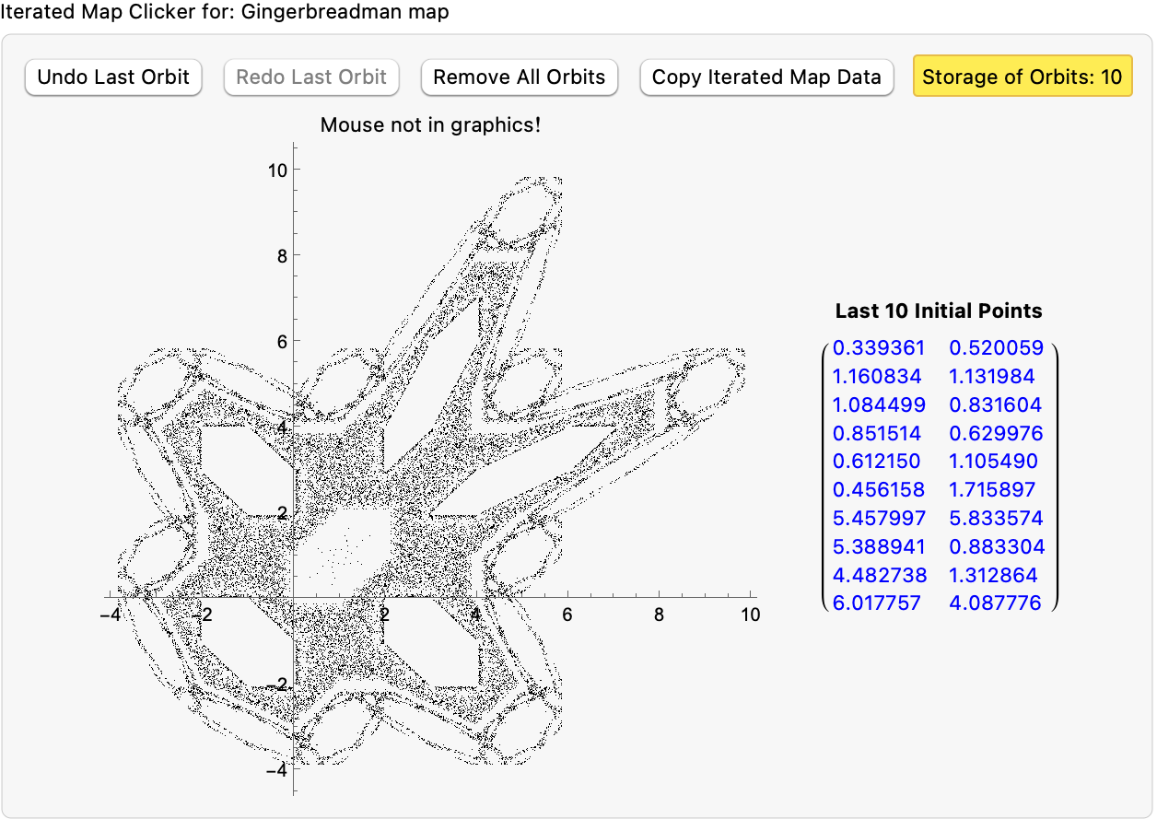

Copy the data generated by ClickRecurrenceMap2D using the Copy Iterated Map Data button:

Publisher

Ramón Eduardo Chan López

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 2.2.0 – 14 February 2025
  • 2.1.1 – 02 October 2023
  • 2.1.0 – 05 July 2023
  • 2.0.0 – 31 May 2023
  • 1.1.0 – 27 March 2023
  • 1.0.0 – 16 September 2022

Source Metadata

  • Citation:
    • Alligood, K.T., Sauer, T.D., Yorke, J.A. (1997). Chaos in Two-Dimensional Maps. In: Chaos. Textbooks in Mathematical Sciences. Springer, Berlin, Heidelberg. DOI: 10.1007/978-3-642-59281-2_5
    • Schuster, H. G., & Just, W. (2006). Deterministic chaos: an introduction. John Wiley & Sons. DOI:10.1002/3527604804
    • Moon, F. C. (2008). Chaotic and fractal dynamics: introduction for applied scientists and engineers. John Wiley & Sons. DOI:10.1002/9783527617500

Related Resources

License Information