Applications (4)
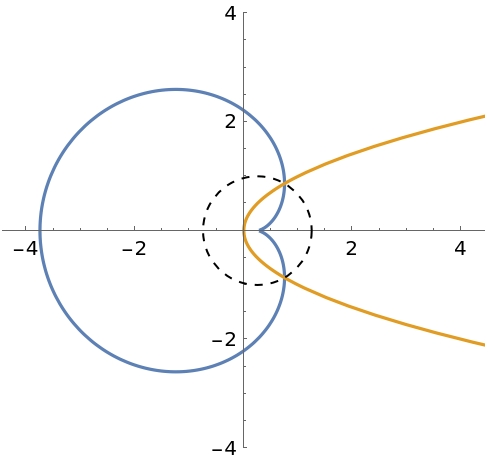
The inverse of a circle is another circle if the original circle does not contain the center of inversion:
The inverse of a circle is a line if the original circle contains the center of inversion:
The inverse of a line is a circle containing the center of inversion if the line does not contain the center:
A line inverts to itself if it contains the center of inversion:
Properties and Relations (3)
CircleInversion is its own inverse:
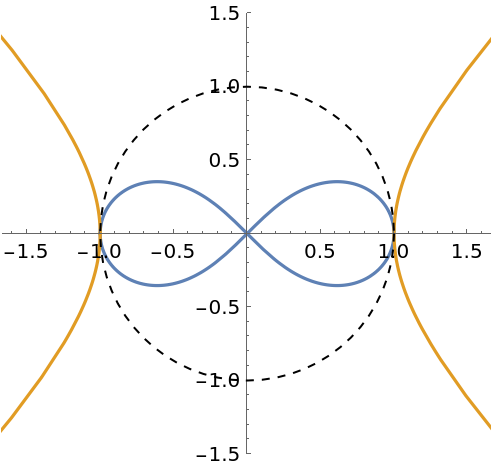
Orthogonal circles are invariant under inversion with respect to each other. However, every point on each circle is inverted to a different place on the same circle (except for the intersection points):
For instance, the point 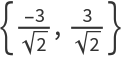 (red) is on the Circle[{0,0},3], which is inverted to a different location (blue) on the same circle:
(red) is on the Circle[{0,0},3], which is inverted to a different location (blue) on the same circle:
Its distance from the origin is still 3:
Regardless of the different types of objects returned by this function, the result of CircleInversion is in general closed under a set of objects recognized by Graphics:
Possible Issues (3)
The inverse of the center of the reference circle is defined as Infinity:
Conversely, the inverse of Infinity is the inversion center:
CircleInversion does not distinguish Line and InfiniteLine as the second argument:
CircleInversion returns different results based on the syntax of InfiniteLine.
For an infinite line that goes through {3,1} and {1,0}, which does not include the inversion center, its image is a circle containing the inversion center:
For an infinite line that passes through {3,1} and is in the same direction as the vector {1,0} (a horizontal line that passes through the inversion center), its image is the line itself:
Neat Examples (3)
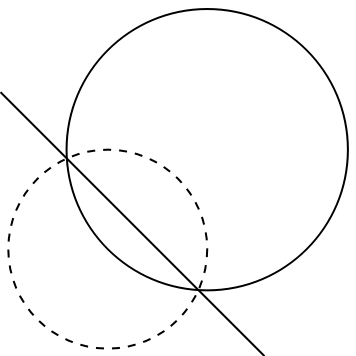
Let three circles have a common point. Suppose that the common chord of two of them is a diameter of the third. If this is true for two of the three common chords, then we can prove that it must be true for all three of them. (C. S. Ogilvy, "Excursions in Geometry").
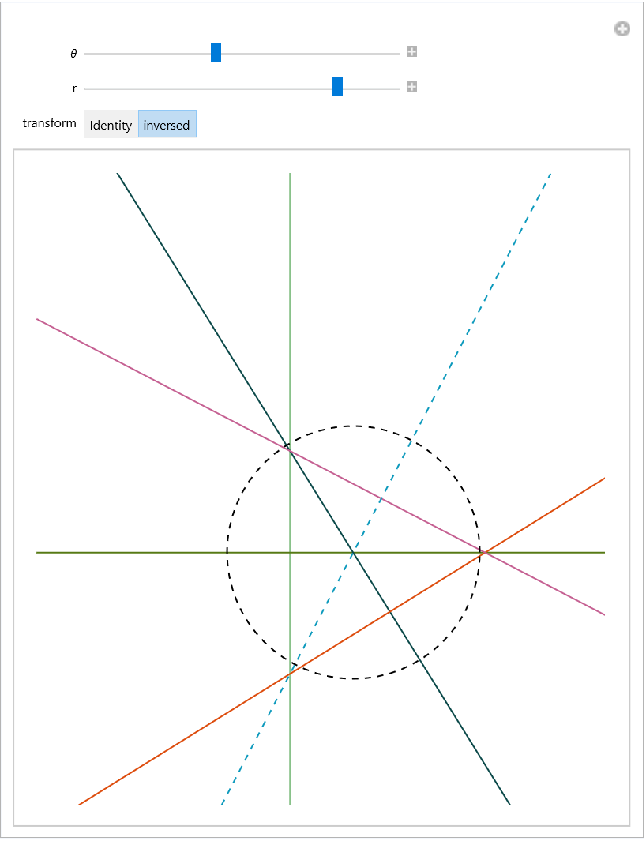
Prove by inversion: Convert the diagram on the left to the one on the right, and complete the proof with the concurrency of three altitudes in any triangle. The center of inversion is the concurrency of three circles:
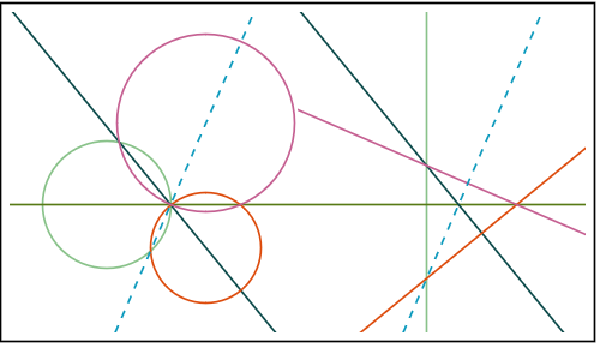
Use Manipulate to see the invariance of the result by changing the configuration of the circles constrained by the statement of the problem:
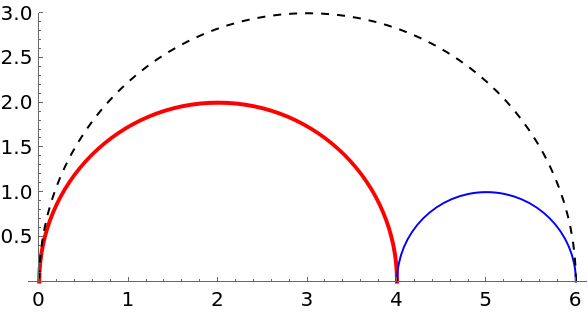
Semicircles with centers at A (red) and B (blue) and with radii 2 and 1, respectively, are drawn in the interior of, and share bases with, a semicircle with diameter JK. The two smaller semicircles are externally tangent to each other and internally tangent to the largest semicircle (dashed). A circle centered at P is drawn externally tangent to the two smaller semicircles and internally tangent to the largest semicircle. What is the radius of the circle centered at P (2017 AMC 12A Problem 16)?
As described previously, the arbelos and chain of Pappus:
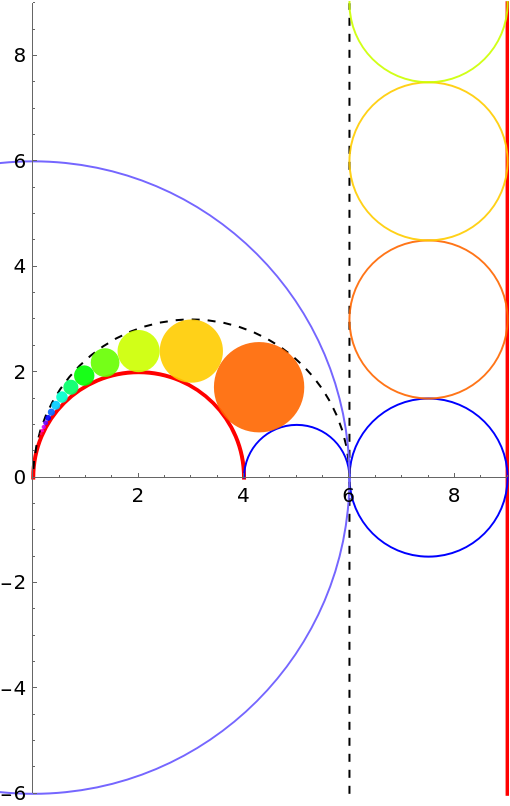
The result to the nth circle in the chain by circle inversion can easily be generalized. Choose the center of inversion to be {0,0} and let the radius of the reference circle be 6 (marked by  as the largest circle in the diagram at the bottom):
as the largest circle in the diagram at the bottom):
If you are looking for the radius of the first 15 circles in the chain, you have:
The framed part is the answer this problem is asking for. In the diagram below, each disk is the element in the chain of Pappus by inverting the circle with the same color from the column on the right:
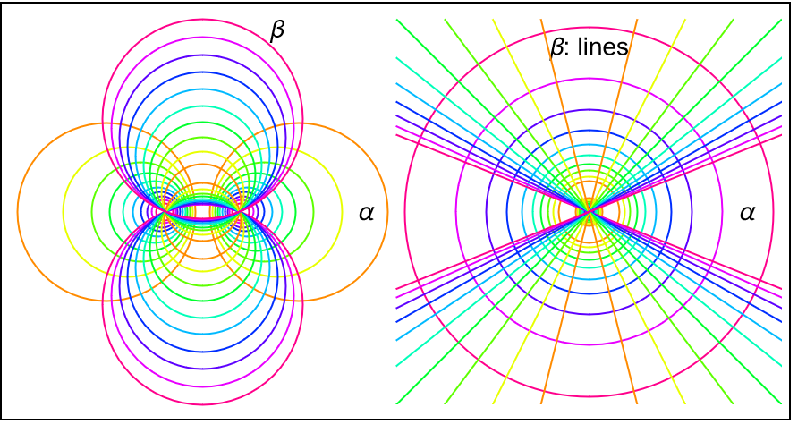
The combination of inversion and a coaxial family (or pencil of circles) is the key step to finding the Steiner chain of two given non-intersecting circles. For 0<|t|<1, there are points 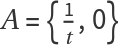 , B={t,0}, C={1,0} and D={-1,0}. Then A and B are harmonic conjugates with respect to C and D. Define the α and β families of circles:
, B={t,0}, C={1,0} and D={-1,0}. Then A and B are harmonic conjugates with respect to C and D. Define the α and β families of circles:
Any pair of circles, one from each family, intersects orthogonally:
Check the dot product of two vectors that sit at each center of the circles and point to the intersection:
This also proves that the locus of the center of circles in the β family (or the perpendicular bisector of segment CD) is the radical axis for any two circles in the α family.
Invert the circles in both coaxial families with respect to the reference circle centered at point C:
The β circles contain the inversion center, and they are thus mapped to lines. The inverses of the α circles are circles, and they must orthogonally intersect the inverses of the β circles. This is due to the anti-conformal property of circle inversion. The only possibility is that the inverse of the α circles are concentric circles with the common center at point C:
The result implies that you only need to consider the case of concentric circles to determine the number of circles in a closed Steiner chain, which is an easy task. This number is invariant under inversion.
![]() :
:
![]() (red) is on the Circle[{0,0},3], which is inverted to a different location (blue) on the same circle:
(red) is on the Circle[{0,0},3], which is inverted to a different location (blue) on the same circle: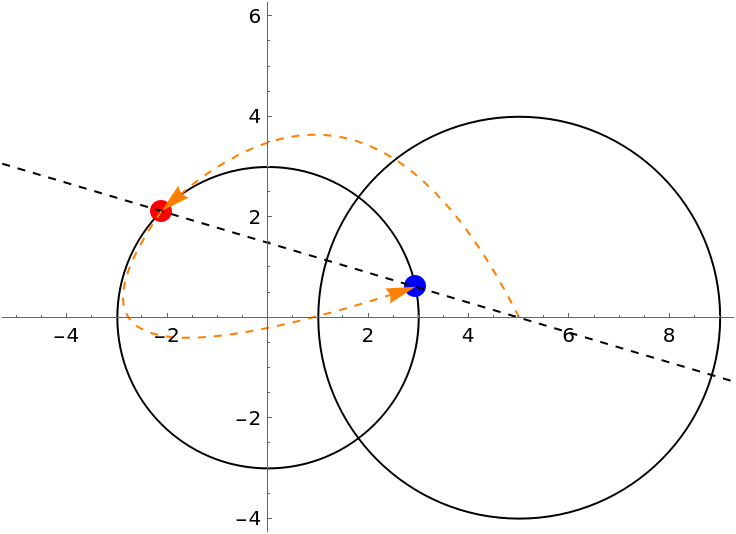
![Graphics[{{Dashed, Circle[{0, 0}, 1]},
Circle[{1, 1}, 1 Sqrt[2]], ResourceFunction["CircleInversion"][Circle[{0, 0}, 1], Circle[{1, 1}, Sqrt[2]]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/716/7162dc6c-9591-4b87-8986-78771a98844f/1-0-1/174462cb13ee5409.png)

![inversed[obj_] := ResourceFunction["CircleInversion"][Circle[{1, 0}, 1], obj];
styles = {{
RGBColor[0.5382014010080749, 0.7621289498025601, 0.5407640169526022]}, {
RGBColor[0.34061930550700836`, 0.47896769701169584`, 0.08332446727427234]}, {
RGBColor[0.043679920724924326`, 0.28684639558982106`, 0.2875297371509651]}, {
RGBColor[0.8662159096842248, 0.2991378845120021, 0.05156033521648418]}, {
RGBColor[0.7724873890185149, 0.37645720497594515`, 0.5712144766631648]}, {RGBColor[
0.04156835207846221, 0.5984264478339989, 0.7367448996675083], Dashing[{Small, Small}]}};
Manipulate[
With[{thirdCircle = CircleThrough[{
pt1[\[Theta]], {1, 0}, {2 Part[
pt2[\[Theta], r], 1] - 1, 0}}]},
Graphics[
Join[
MapThread[Append, {styles,
Map[transform, {
Circle[{0, 0}, 1],
InfiniteLine[{0, 0}, {1, 0}],
InfiniteLine[{
pt1[\[Theta]],
pt2[\[Theta], r]}],
Circle[
pt2[\[Theta], r], r], thirdCircle,
InfiniteLine[{
Part[thirdCircle, 1], {1, 0}}]}]}], {{Dashed,
Circle[{1, 0}, 1]}}], PlotRange -> {{-1.5, 3}, {-2, 3}}]], {{\[Theta],
Pi/3.5}, Pi/4, Pi/2}, {r, 0.5, 1}, {transform, {Identity, inversed}}, ControlPlacement -> Top, SaveDefinitions -> True, Initialization :> (pt1[
Pattern[\[Theta],
Blank[]]] := {
Cos[\[Theta]],
Sin[\[Theta]]}; pt2[
Pattern[\[Theta],
Blank[]],
Pattern[r,
Blank[]]] := Normalize[{1, 0} - {
Cos[\[Theta]],
Sin[\[Theta]]}] r + {1, 0}; Null)]](https://www.wolframcloud.com/obj/resourcesystem/images/716/7162dc6c-9591-4b87-8986-78771a98844f/1-0-1/6f75f7ac7825bb74.png)
![attributes = {{Red, Thick}, {Blue}, {Black, Dashed}};
objList1 = MapThread[
Append, {attributes, {Circle[{2, 0}, 2, {0, \[Pi]}], Circle[{5, 0}, 1, {0, \[Pi]}], Circle[{3, 0}, 3, {0, \[Pi]}]}}];
Graphics[objList1, Axes -> True, PlotRange -> {0, 3}]](https://www.wolframcloud.com/obj/resourcesystem/images/716/7162dc6c-9591-4b87-8986-78771a98844f/1-0-1/6817d52eccaf7e30.png)
![]() as the largest circle in the diagram at the bottom):
as the largest circle in the diagram at the bottom):![n = 15;
imagebase = inverse2[Circle[{5, 0}, 1]];
circleList1 = Table[Circle[imagebase[[1]] + 2*{0, imagebase[[2]]*k}, imagebase[[2]]], {k, 1, n}];](https://www.wolframcloud.com/obj/resourcesystem/images/716/7162dc6c-9591-4b87-8986-78771a98844f/1-0-1/5bd962127d0ea25f.png)
![objList2 = MapThread[
Append, {attributes, inverse2 /@ {Circle[{2, 0}, 2], Circle[{5, 0}, 1], Circle[{3, 0}, 3]}}];
disks = ((inverse2 /@ circleList1) // Simplify) /. Circle -> Disk;
hueList = {Hue[#], Opacity[0.9]} & /@ (Range[n]/n);
Graphics[objList1~Join~MapThread[Append, {hueList, disks}]~Join~
objList2~Join~MapThread[Append, {hueList, circleList1}]~
Join~{{RGBColor[0.46, 0.4, 1], Circle[{0, 0}, 6]}}, Axes -> True, PlotRange -> {{0, 9}, {-6, 9}}]](https://www.wolframcloud.com/obj/resourcesystem/images/716/7162dc6c-9591-4b87-8986-78771a98844f/1-0-1/2d2a8b003cec87ea.png)
![]() , B={t,0}, C={1,0} and D={-1,0}. Then A and B are harmonic conjugates with respect to C and D. Define the α and β families of circles:
, B={t,0}, C={1,0} and D={-1,0}. Then A and B are harmonic conjugates with respect to C and D. Define the α and β families of circles:![pt1 = FullSimplify[
ResourceFunction[
ResourceObject[<|"Name" -> "CircleIntersection", "ShortName" -> "CircleIntersection", "UUID" -> "7560a8c9-f5e8-4a4d-a75d-6f79737eea04", "ResourceType" -> "Function", "Version" -> "1.0.0", "Description" -> "Find the intersection of two circles", "RepositoryLocation" -> URL[
"https://www.wolframcloud.com/obj/resourcesystem/api/1.0"], "SymbolName" -> "FunctionRepository`$f4a0b2b9f9ef4a9997eb139de10dc92a`CircleIntersection", "FunctionLocation" -> CloudObject[
"https://www.wolframcloud.com/obj/9bb5c165-2189-4106-b81a-cf6b395625ff"]|>, ResourceSystemBase -> Automatic]][
betaFamily[\[Lambda]], alphaFamily[t]],
Assumptions -> t > 0 && \[Lambda] > 0][[1, 1]]](https://www.wolframcloud.com/obj/resourcesystem/images/716/7162dc6c-9591-4b87-8986-78771a98844f/1-0-1/0343d32a99d4854b.png)
![style = {{
Hue[
Rational[10, 11]]}, {
Hue[
Rational[9, 11]]}, {
Hue[
Rational[8, 11]]}, {
Hue[
Rational[7, 11]]}, {
Hue[
Rational[6, 11]]}, {
Hue[
Rational[5, 11]]}, {
Hue[
Rational[4, 11]]}, {
Hue[
Rational[3, 11]]}, {
Hue[
Rational[2, 11]]}, {
Hue[
Rational[1, 11]]}, {
Hue[
Rational[1, 11]]}, {
Hue[
Rational[2, 11]]}, {
Hue[
Rational[3, 11]]}, {
Hue[
Rational[4, 11]]}, {
Hue[
Rational[5, 11]]}, {
Hue[
Rational[6, 11]]}, {
Hue[
Rational[7, 11]]}, {
Hue[
Rational[8, 11]]}, {
Hue[
Rational[9, 11]]}, {
Hue[
Rational[10, 11]]}};
\[Lambda]List = {-(5/2), -(9/4), -2, -(7/4), -(3/2), -(5/4), -1, -(
3/4), -(1/2), -(1/4), 1/4, 1/2, 3/4, 1, 5/4, 3/2, 7/4, 2, 9/4, 5/2};
tList = {-0.8, -0.7333333333333334, -0.6666666666666667, -0.6000000000000001, -0.5333333333333334, -0.46666666666666673`, -0.4, -0.33333333333333337`, -0.2666666666666667, -0.20000000000000007`, 0.2, 0.26666666666666666`, 0.33333333333333337`, 0.4, 0.4666666666666667, 0.5333333333333333, 0.6000000000000001, 0.6666666666666667, 0.7333333333333334, 0.8};
af = alphaFamily /@ tList;
bf = betaFamily /@ \[Lambda]List;
afInv = ResourceFunction["CircleInversion"][Circle[{1, 0}, 2], #] & /@
af;
bfInv = ResourceFunction["CircleInversion"][Circle[{1, 0}, 2], #] & /@
bf;](https://www.wolframcloud.com/obj/resourcesystem/images/716/7162dc6c-9591-4b87-8986-78771a98844f/1-0-1/555318e18f3d423b.png)
![applyStyle[style_, objs_] := MapThread[Append, {style, objs}]
Style[Row[{
Graphics[{
Text[
Style["\[Alpha]", 14], {4.4, 0}],
Text[
Style["\[Beta]", 14], {2., 4.9}]}~
Join~(applyStyle[style, #] & /@ {af, bf})],
Graphics[{
Text[
Style["\[Alpha]", 14], {14.4, 0}],
Text[
Style["\[Beta]: lines", 14], {-1, 16.}]}~
Join~(applyStyle[style, #] & /@ {afInv, bfInv})]}],
ImageSizeMultipliers -> 0.6] // Framed // Rasterize](https://www.wolframcloud.com/obj/resourcesystem/images/716/7162dc6c-9591-4b87-8986-78771a98844f/1-0-1/6bd2447baced7c7c.png)