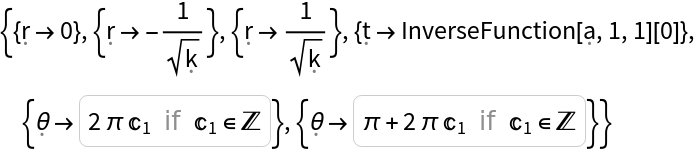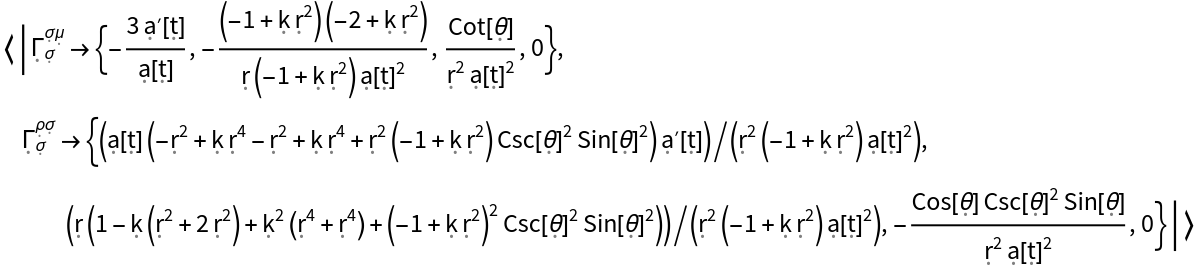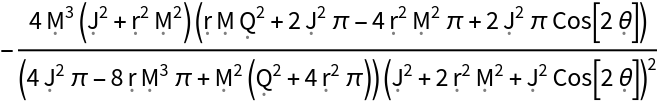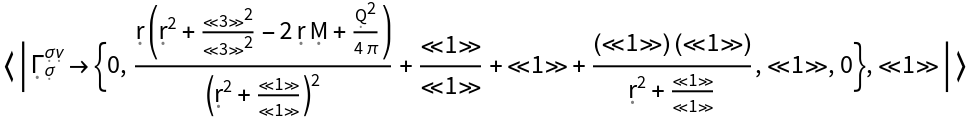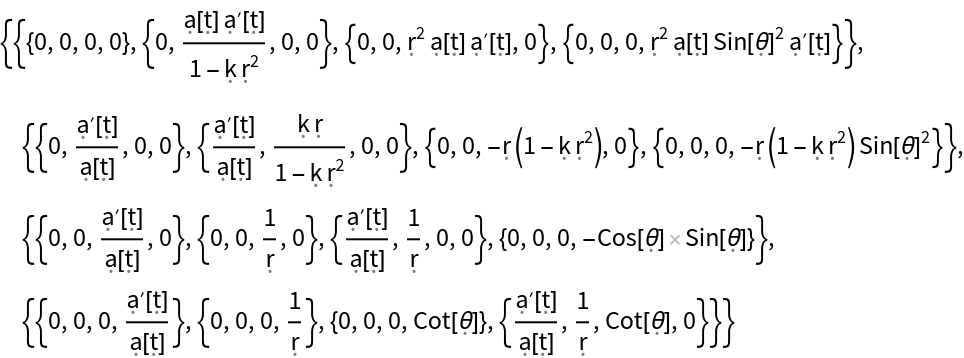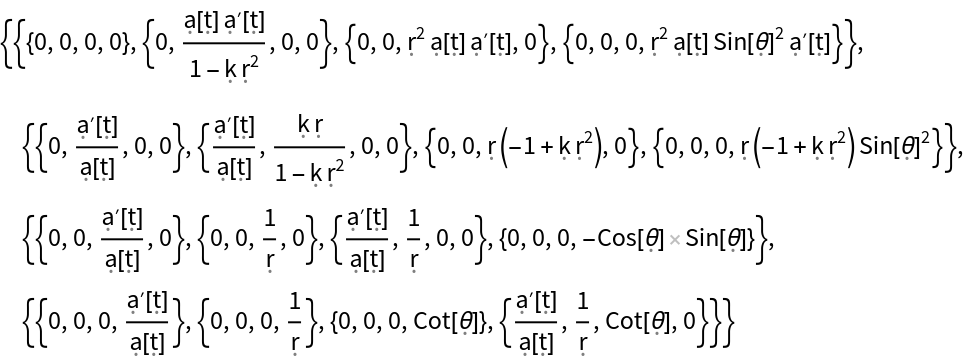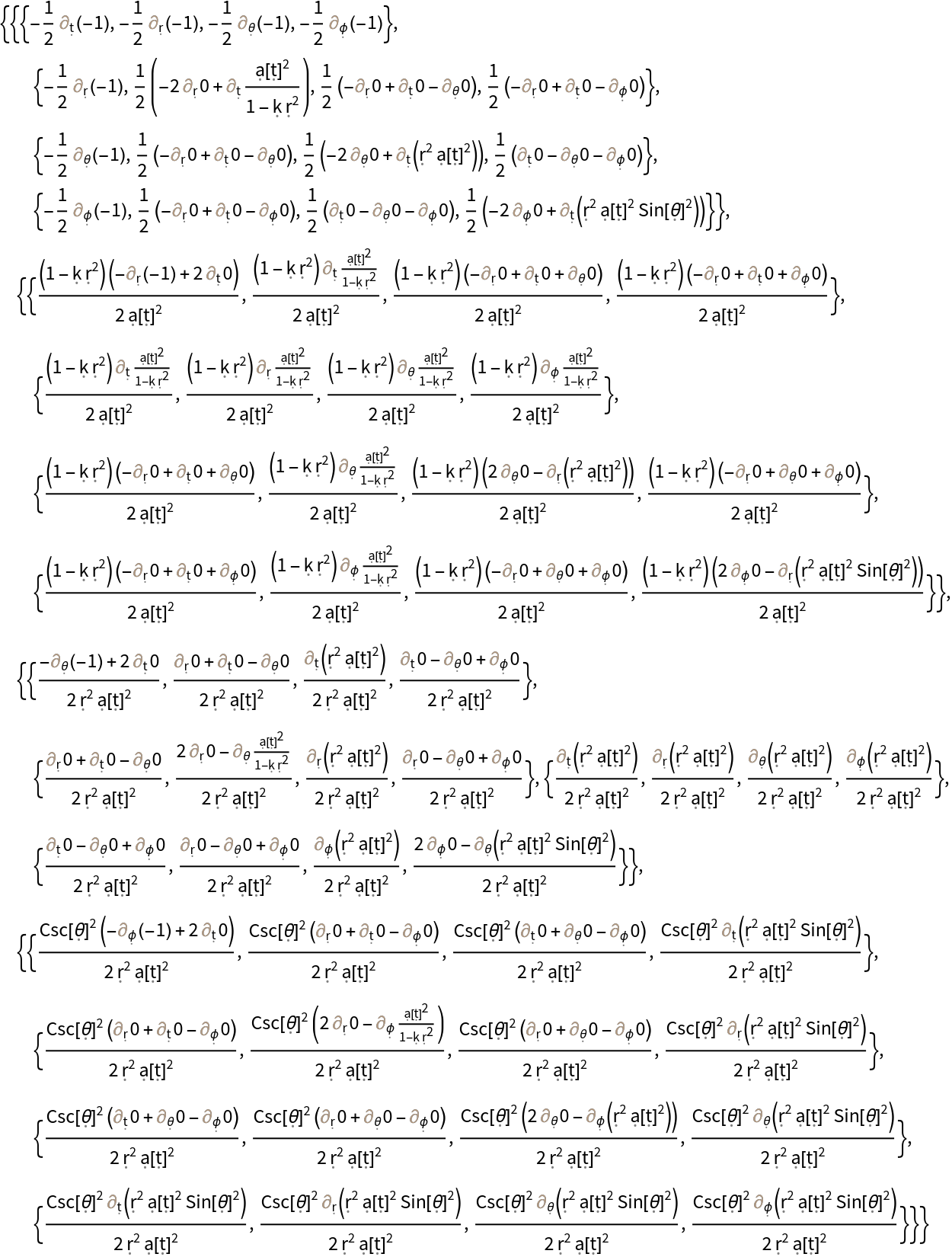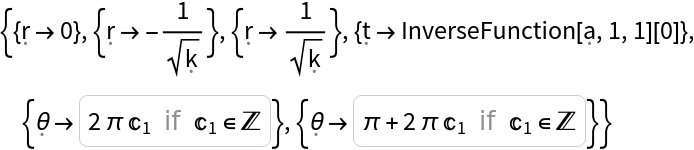Function Repository Resource:

ChristoffelSymbols

Represent the Christoffel symbols for (the Levi-Civita connection over) a Riemannian or pseudo-Riemannian manifold

Contributed by: Jonathan Gorard

ResourceFunction["ChristoffelSymbols"][MetricTensor[…],i₁,i₂,i₃]

represents the Christoffel symbols associated to (the Levi-Civita connection over) the given MetricTensor, with indices i₁,i₂ and i₃ (with True repesenting a covariant index and False representing a contravariant one).

ResourceFunction["ChristoffelSymbols"][ResourceFunction["ChristoffelSymbols"][…],coords]

transforms the specified ResourceFunction["ChristoffelSymbols"] into the new coordinate system coords.

ResourceFunction["ChristoffelSymbols"][ResourceFunction["ChristoffelSymbols"][…],i₁,i₂,i₃]

transforms the specified ResourceFunction["ChristoffelSymbols"] into those with new indices i₁,i₂ and i₃ (with True representing a covariant index and False representing a contravariant one), raising and lowering indices as necessary.

ResourceFunction["ChristoffelSymbols"][ResourceFunction["ChristoffelSymbols"][…],coords,i₁,i₂,i₃]

transforms the specified ResourceFunction["ChristoffelSymbols"] into those with new coordinate system coords and new indices i₁,i₂ and i₃ (with True representing a covariant index and False representing a contravariant one), raising and lowering existing indices as necessary.

Details

Formally, the Christoffel symbols are the components/structure coefficients of the Levi-Civita (i.e. metric) connection over a manifold, defined with respect to a local coordinate basis. The Levi-Civita connection is the unique affine connection on the tangent bundle of a manifold (an affine connection being a geometrical object which connects neighboring tangent spaces together, thus allowing tangent vector fields to be differentiated on the manifold) that is both torsion-free and preserves the Riemannian (or pseudo-Riemannian) metric. Informally, the Christoffel symbols define how the basis vectors of the coordinate system change as one moves from point to point on the manifold.

Strictly speaking, the Christoffel symbols are three-dimensional arrays of numbers, defined at specified points on a manifold, rather than true rank-3 tensors (or tensor fields). Specifically, the Christoffel symbols only transform like components of a tensor under linear coordinate transformations, rather than under the more general diffeomorphism transformations of tensor calculus. However, in most other respects (e.g. the rules for raising and lowering indices, contracting indices, etc.) they behave algebraically like rank-3 tensors, and are consequently treated as such by ResourceFunction["ChristoffelSymbols"].

By default, ResourceFunction["ChristoffelSymbols"][MetricTensor[…],i₁,i₂,i₃] represents the Christoffel symbols by an array representation of linear combinations of partial derivatives of the metric tensor in a given coordinate basis, such that the entries of this array transform either covariantly or contravariantly, or some mixture of the two, with respect to (linear) transformations of the coordinates. The indices i₁, i₂ and i₃ can either be set to True (covariant) or False (contravariant). By default, the first index is set to False (i.e. contravariant) and the latter two are set to True (i.e. covariant), thus yielding Christoffel symbols of the second kind. If the first index is set to True instead (i.e. all components of the array transform covariantly), one obtains Christoffel symbols of the first kind.

In differential geometry, the mathematical significance of the Christoffel symbols is that, just like the components/structure coefficients of any affine connection, they allow one to define consistent notions of parallel transport, covariant differentiation and curvature on any (pseudo-)Riemannian manifold via the theory of (pseudo-)Riemannian holonomy. In general relativity, where spacetime is typically regarded as being torsion-free, the physical significance of the Christoffel symbols is that they effectively represent a gravitational force field whose gravitational potential is given by the metric tensor.

ResourceFunction["ChristoffelSymbols"] does not assume any particular number of dimensions, nor any particular metric convention, for the underlying manifold (although some properties, such as "LorentzianConditions", implicitly assume a (-,+,+,+,…) signature). ResourceFunction["ChristoffelSymbols"] also does not require the metric to be strictly symmetric (i.e. non-zero contorsion tensors are also supposed), although the torsion-free Levi-Civita connection is always assumed.

ResourceFunction["ChristoffelSymbols"] implicitly keeps track of all known algebraic equivalences between tensor expressions, and can apply them for simplification purposes where necessary. Requesting any property with "Reduced" in its name has the effect of applying all known tensor equivalences and simplifying (note that this can have the effect of increasing computation time significantly).

By default, ResourceFunction["ChristoffelSymbols"] evaluates all partial derivatives of the metric tensor automatically. In certain cases, however, these partial derivatives may be difficult or even impossible to compute, in which case the evaluation may not terminate in a reasonable time. Requesting any property with "Symbolic" in its name has the effect of leaving all partial derivatives unevaluated instead (note that this can have the effect of increasing expression length significantly).

If the function succeeds in constructing the specified Christoffel symbols, it will return a ResourceFunction["ChristoffelSymbols"] expression.

Calling ResourceFunction["ChristoffelSymbols"][…][i,j,k] returns the entry in the i-th layer, j-th column and k-th row of the array representation of the Christoffel symbols.

Calling ResourceFunction["ChristoffelSymbols"][ResourceFunction["ChristoffelSymbols"][…],coords] has the effect of transforming the metric tensor (and hence the Christoffel symbols) to the new coordinate system coords. Calling ResourceFunction["ChristoffelSymbols"][ResourceFunction["ChristoffelSymbols"][…],i₁,i₂,i₃] has the effect of raising and lowering appropriate indices of the Christoffel symbols to match i₁, i₂ and i₃ (with True representing lowered/covariant and False representing raised/contravariant). Calling ResourceFunction["ChristoffelSymbols"][ResourceFunction["ChristoffelSymbols"][…],coords,i₁,i₂,i₃] has the effect of performing both transformations simultaneously.

By default, ResourceFunction["ChristoffelSymbols"] keeps track of the positions of all indices and performs all raising and lowering operations automatically, as required for a given computation.

Based on the eigenvalues of the matrix representation of the underlying metric tensor in covariant form, the underlying manifold will be classified by ResourceFunction["ChristoffelSymbols"] as either Riemannian (all eigenvalues positive or all eigenvalues negative), pseudo-Riemannian (some eigenvalues positive and some eigenvalues negative), Lorentzian (all eigenvalues positive except for one negative, or all eigenvalues negative except for one positive) or Indeterminate.

The property "RiemannianConditions" returns the conditions necessary to guarantee that the eigenvalues of the matrix representation of the underlying metric tensor are strictly positive; "PseudoRiemannianConditions" returns the conditions necessary to guarantee that the eigenvalues of the matrix representation of the underlying metric tensor are all non-zero; "LorentzianConditions" returns the conditions necessary to guarantee that the eigenvalue corresponding to the {1,0,0,…} eigenvector of the underlying metric tensor (if it exists) is negative, with all other eigenvalues being positive. Note that this is strictly less general than the behavior of properties such as "RiemannianQ" (described in the point above), since it assumes certain features of the metric signature.

In ResourceFunction["ChristoffelSymbols"], the following properties are supported:

"TensorRepresentation"

Christoffel symbols represented in explicit array form

"ReducedTensorRepresentation"

Christoffel symbols represented in explicit array form, modulo all tensor equivalences

"SymbolicTensorRepresentation"

Christoffel symbols represented in explicit array form, with purely symbolic partial derivative operators

"MetricTensor"

underlying metric tensor associated to the Christoffel symbols

"Coordinates"

list of coordinate symbols for the Christoffel symbols

"CoordinateOneForms"

list of differential 1-form symbols for the coordinates of the Christoffel symbols

"Indices"

list of booleans specifying whether each index of the Christoffel symbols is lowered/covariant (True) or raised/contravariant (False)

"CovariantQ"

whether the Christoffel symbols are covariant (i.e. all indices are lowered/covariant)

"ContravariantQ"

whether the Christoffel symbols are contravariant (i.e. all indices are raised/contravariant)

"MixedQ"

whether the Christoffel symbols are mixed (i.e. some indices are lowered/covariant and some indices are raised/contravariant)

"Symbol"

symbolic representation of the Christoffel symbols with appropriately raised/lowered indices

"VanishingChristoffelQ"

whether all components of the Christoffel symbols vanish

"VanishingChristoffelConditions"

list of conditions required to guarantee that all components of the Christoffel symbols vanish

"IndexContractions"

association of possible index contractions of the Christoffel symbols

"ReducedIndexContractions"

association of possible index contractions of the Christoffel symbols, modulo all tensor equivalences

"SymbolicIndexContractions"

association of possible index contractions of the Christoffel symbols, with purely symbolic partial derivative operators

"Dimensions"

number of dimensions of the underlying manifold/spacetime described by the Christoffel symbols

"Signature"

list of +1s and -1s designating the signature of the underlying manifold described by the Christoffel symbols (+1 for each positive eigenvalue of the metric, -1 for each negative eigenvalue of the metric)

"RiemannianQ"

whether the underlying manifold described by the Christoffel symbols is Riemannian (i.e. all eigenvalues of the metric have the same sign)

"PseudoRiemannianQ"

whether the underlying manifold described by the Christoffel symbols is pseudo-Riemannian (i.e. all eigenvalues of the metric are non-zero, but not all have the same sign)

"LorentzianQ"

whether the underlying manifold described by the Christoffel symbols is Lorentzian (i.e. all eigenvalues of the metric have the same sign, except for one eigenvalue which has the opposite sign)

"RiemannianConditions"

list of conditions required to guarantee that the underlying manifold described by the Christoffel symbols is Riemannian (i.e. all eigenvalues of the metric are positive)

"PseudoRiemannianConditions"

list of conditions required to guarantee that the underlying manifold described by the Christoffel symbols is pseudo-Riemannian (i.e. all eigenvalues of the metric are non-zero)

"LorentzianConditions"

list of conditions required to guarantee that the underlying manifold described by the Christoffel symbols is Lorentzian (i.e. the "time" eigenvalue of the metric is negative and all other eigenvalues are positive)

"ConnectionSingularities"

list of possible coordinate values that cause the Christoffel symbols to become singular

"CovariantChristoffelSymbols"

covariant form of the Christoffel symbols (i.e. all indices are lowered/covariant)

"ContravariantChristoffelSymbols"

contravariant form of the Christoffel symbols (i.e. all indices are raised/contravariant)

"Properties"

list of properties

Examples

Basic Examples (3)

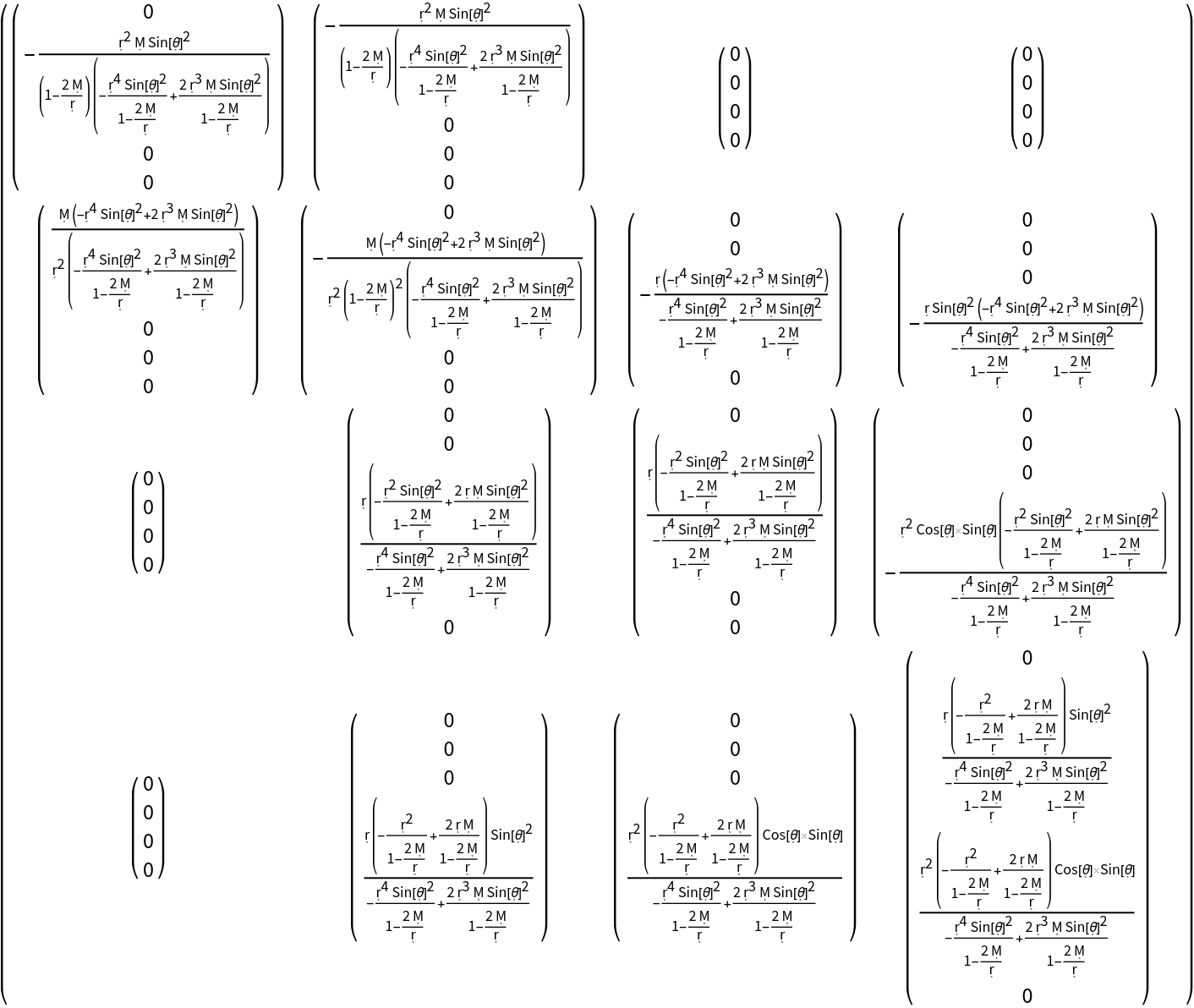
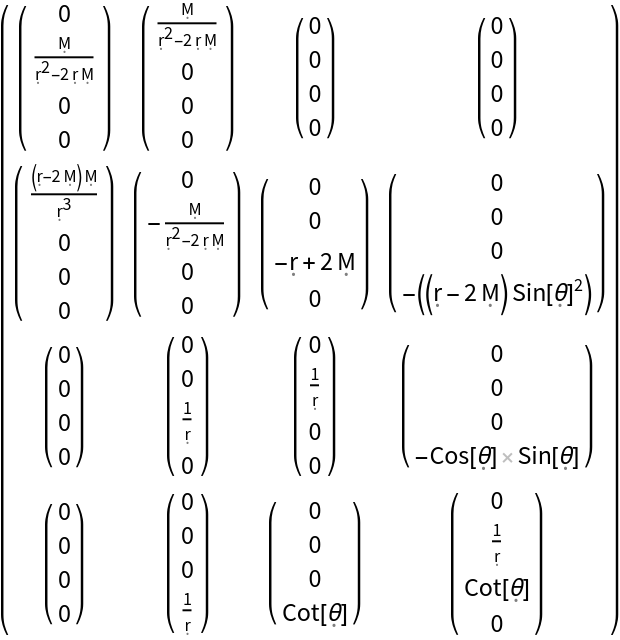
Construct the Christoffel symbols for the Schwarzschild metric (e.g. for an uncharged, non-rotating black hole with symbolic mass "M") in standard spherical polar coordinates:

In[1]:=

Out[1]=

In[2]:=

Out[2]=

Show the Christoffel symbols for the Schwarzschild metric in explicit (mixed) array form:

In[3]:=

Out[3]=

Show the Christoffel symbols for the Schwarzschild metric in explicit (mixed) array form, with all algebraic equivalences imposed:

In[4]:=

Out[4]=

Deduce that the Christoffel symbols for the Schwarzschild metric do not vanish:

In[5]:=

Out[5]=

Show the list of Schwarzschild coordinate symbols:

In[6]:=

Out[6]=

Show the list of differential 1-form symbols for each of the Schwarzschild coordinates:

In[7]:=

Out[7]=

Show the list of coordinate conditions that must hold for the Schwarzschild metric to be Lorentzian:

In[8]:=

Out[8]=

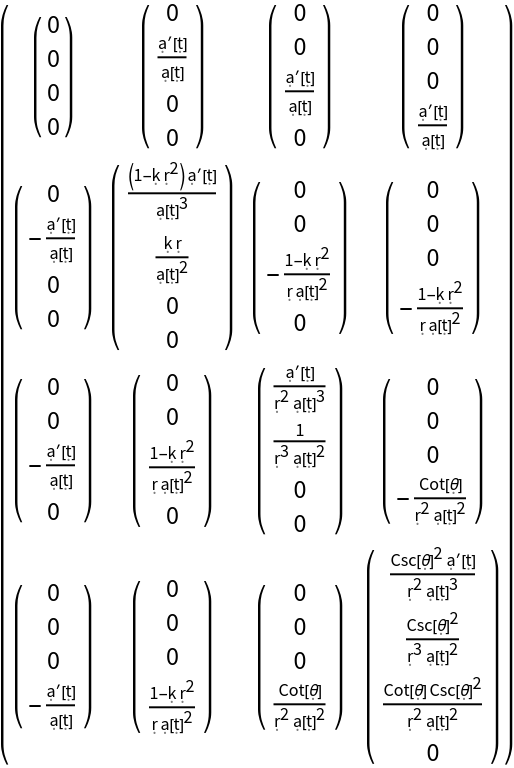
Construct the Christoffel symbols for the Friedmann-Lemaître-Robertson-Walker (FLRW) metric (for a homogeneous, isotropic and uniformly-expanding/contracting universe, with symbolic curvature parameter "k" and symbolic scale factor "a") in standard spherical polar coordinates:

In[9]:=

Out[9]=

In[10]:=

Out[10]=

In[11]:=

Out[11]=

Show the list of coordinate values that cause the Christoffel symbols for the FLRW metric to become singular:

In[12]:=

Out[12]=

Show the association of all possible index contractions of the Christoffel symbols for the FLRW metric:

In[13]:=

Out[13]=

Show the association of all possible index contractions of the Christoffel symbols for the FLRW metric, with all algebraic equivalences imposed:

In[14]:=

Out[14]=

Raise the second index of the Christoffel symbols for the FLRW metric:

In[15]:=

Out[15]=

In[16]:=

Out[16]=

Show the association of all possible index contractions of the Christoffel symbols (with second index raised) for the FLRW metric:

In[17]:=

Out[17]=

Show the association of all possible index contractions of the Christoffel symbols (with second index raised) for the FLRW metric, with all algebraic equivalences imposed:

In[18]:=

Out[18]=

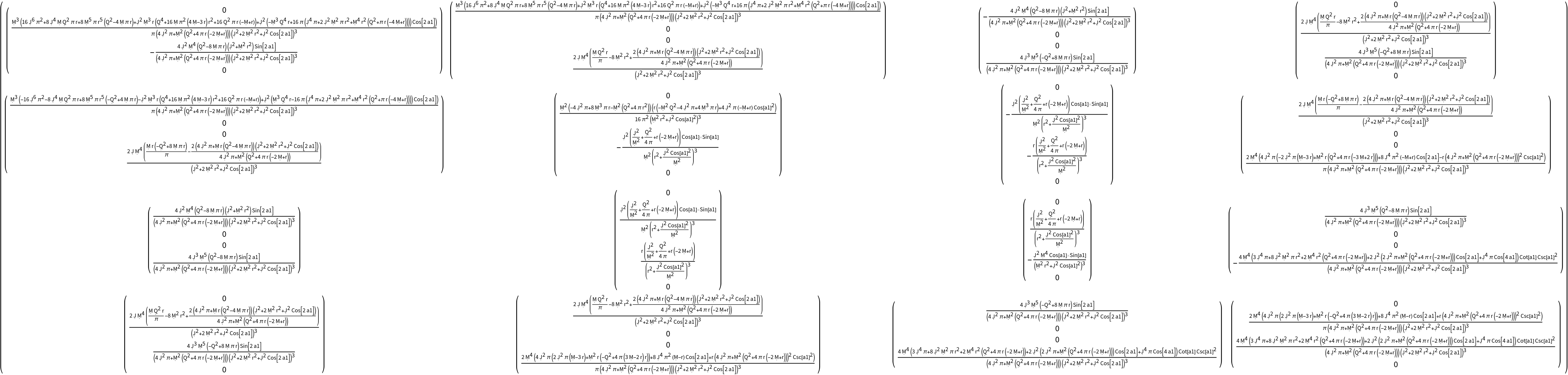
Construct the Christoffel symbols for the Kerr-Newman metric (e.g. for a charged, spinning black hole with symbolic mass "M", symbolic angular momentum "J" and symbolic electric charge "Q") in Boyer-Lindquist/oblate spheroidal coordinates:

In[19]:=

Out[19]=

In[20]:=

Out[20]=

In[21]:=

Out[21]=

Extract (and simplify) the time-time-radial component of the Christoffel symbols for the Kerr-Newman metric:

In[22]:=

Out[22]=

Deduce that the Christoffel symbols for the Kerr-Newman metric do not vanish:

In[23]:=

Out[23]=

Show the list of conditions that must hold for the Christoffel symbols for the Kerr-Newman metric to vanish:

In[24]:=

Out[24]=

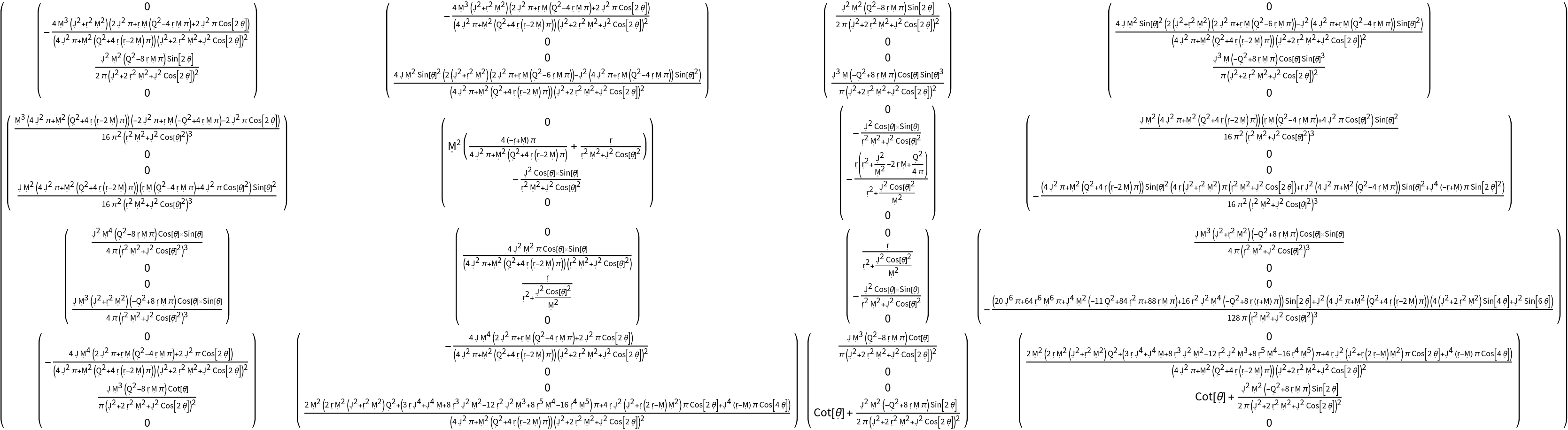
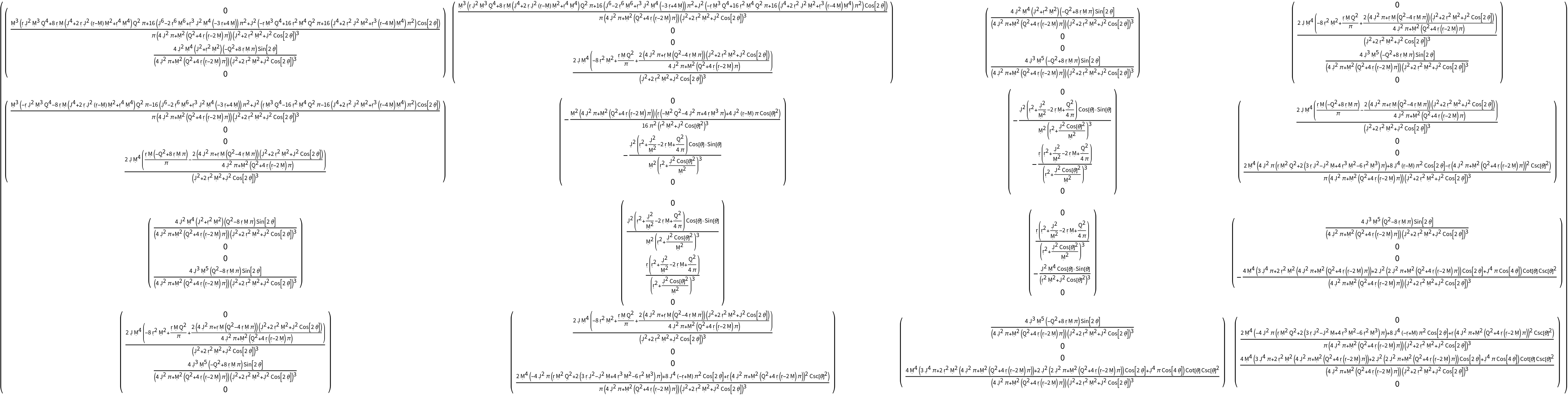
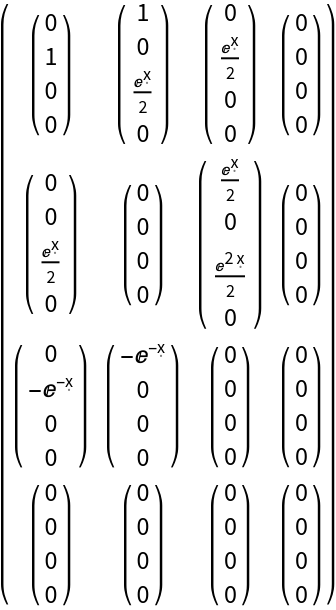
Compute the covariant form of the Christoffel symbols (with all indices lowered):

In[25]:=

Out[25]=

In[26]:=

Out[26]=

In[27]:=

Out[27]=

In[28]:=

Out[28]=

Show that no index contractions are possible for the Christoffel symbols in covariant form:

In[29]:=

Out[29]=

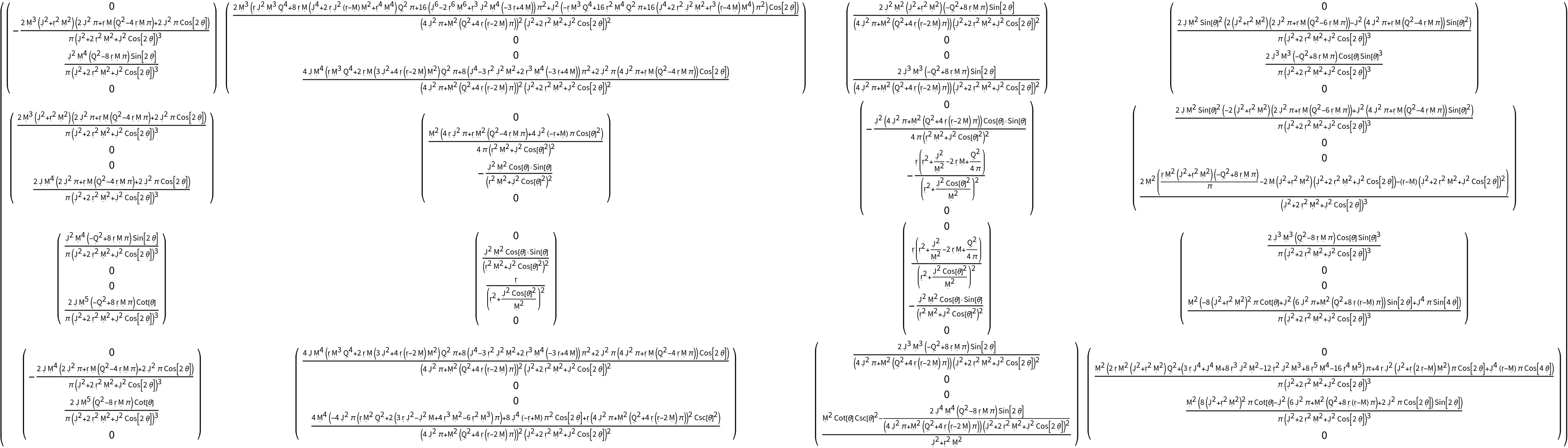
Compute the contravariant form of the Christoffel symbols (with all indices raised):

In[30]:=

Out[30]=

In[31]:=

Out[31]=

In[32]:=

Out[32]=

In[33]:=

Out[33]=

Show that no index contractions are possible for the Christoffel symbols in contravariant form:

In[34]:=

Out[34]=

Compute a mixed form of the Christoffel symbols with the first and last indices raised/contravariant and the second index lowered/covariant:

In[35]:=

Out[35]=

In[36]:=

Out[36]=

In[37]:=

Out[37]=

In[38]:=

Out[38]=

Show that index contractions are only possible for the Christoffel symbols in mixed form:

In[39]:=

Out[39]=

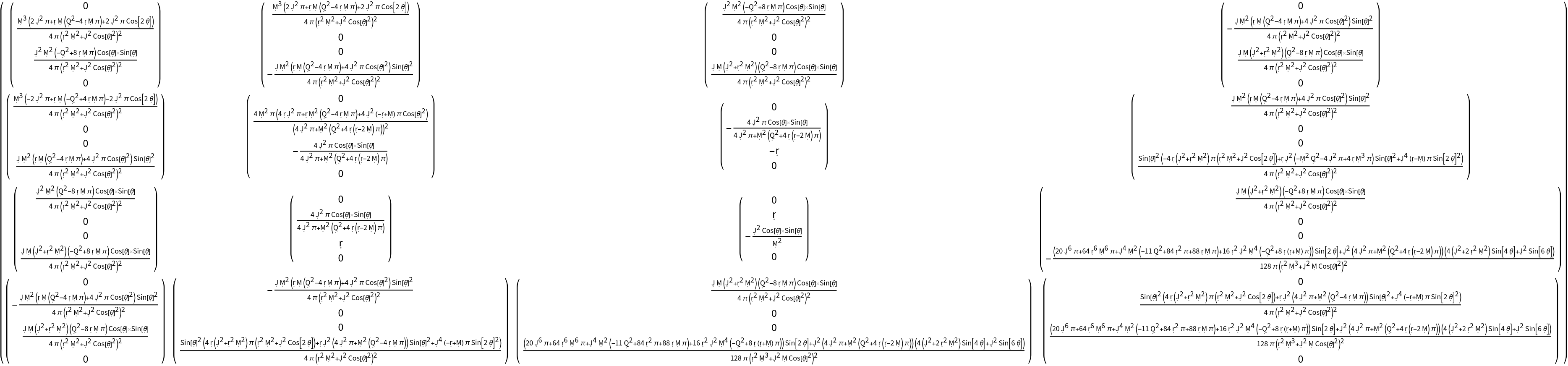
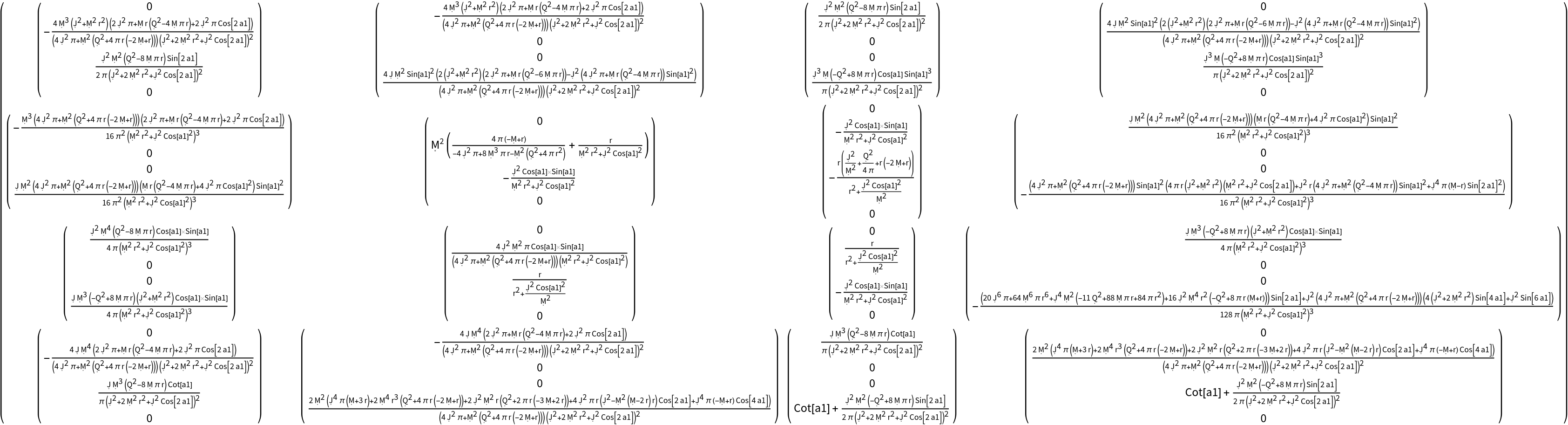
Transform to use the new coordinate symbols t, r, a1 and a2:

In[40]:=

Out[40]=

In[41]:=

Out[41]=

Transform to use the new coordinate symbols t, r, a1 and a2, and raise all indices, simultaneously:

In[42]:=

Out[42]=

In[43]:=

Out[43]=

Scope (3)

Christoffel symbols can be constructed directly from a MetricTensor expression:

In[44]:=

Out[44]=

In[45]:=

Out[45]=

In[46]:=

Out[46]=

Additional arguments can be used to specify the coordinate symbols (otherwise default symbols will be chosen automatically):

In[47]:=

Out[47]=

In[48]:=

Out[48]=

In[49]:=

Out[49]=

Or the indices (True for lowered/covariant and False for raised/contravariant - otherwise the first index will be set as raised/contravariant and the latter two as lowered/covariant by default):

In[50]:=

Out[50]=

In[51]:=

Out[51]=

Or both simultaneously:

In[52]:=

Out[52]=

In[53]:=

Out[53]=

In[54]:=

Out[54]=

New coordinate symbols can be specified for any Christoffel symbols:

In[55]:=

Out[55]=

In[56]:=

Out[56]=

In[57]:=

Out[57]=

In[58]:=

Out[58]=

Indices can also be raised and lowered on any Christoffel symbol:

In[59]:=

Out[59]=

In[60]:=

Out[60]=

New coordinate symbols and new index positions can also be specified simultaneously:

In[61]:=

Out[61]=

In[62]:=

Out[62]=

In[63]:=

Out[63]=

Construct the Christoffel symbols for the FLRW metric, with symbolic curvature parameter "k" and symbolic scale factor "a":

In[64]:=

Out[64]=

In[65]:=

Out[65]=

Show the list of properties:

In[66]:=

Out[66]=

Show the explicit array representation of the Christoffel symbols:

In[67]:=

Out[67]=

Show the explicit array representation of the Christoffel symbols, with all algebraic equivalences imposed:

In[68]:=

Out[68]=

Show the explicit array representation of the Christoffel symbols, with all partial derivative operators left purely symbolic:

In[69]:=

Out[69]=

Show the metric tensor for the underlying manifold represented by the Christoffel symbols:

In[70]:=

Out[70]=

Show the list of coordinate symbols for the Christoffel symbols:

In[71]:=

Out[71]=

Show the list of differential 1-form symbols for the coordinates of the Christoffel symbols:

In[72]:=

Out[72]=

Show the list of booleans specifying the positions of the indices of the Christoffel symbols (True for lowered/covariant and False for raised/contravariant):

In[73]:=

Out[73]=

Determine whether the Christoffel symbols are covariant (i.e. all indices are lowered/covariant):

In[74]:=

Out[74]=

Determine whether the Christoffel symbols are contravariant (i.e. all indices are raised/contravariant):

In[75]:=

Out[75]=

Determine whether the Christoffel symbols are mixed (i.e. some indices are lowered/covariant and some indices are raised/contravariant):

In[76]:=

Out[76]=

Show a symbolic representation of the Christoffel symbols with appropriately raised/lowered indices:

In[77]:=

Out[77]=

Determine whether all components of the Christoffel symbols vanish:

In[78]:=

Out[78]=

Show the list of conditions required to guarantee that all components of the Christoffel symbols vanish:

In[79]:=

Out[79]=

Show the association of all possible index contractions of the Christoffel symbols:

In[80]:=

Out[80]=

Show the association of all possible index contractions of the Christoffel symbols, with all algebraic equivalences imposed:

In[81]:=

Out[81]=

Show the association of all possible index contractions of the Christoffel symbols, with all partial derivative operators left purely symbolic:

In[82]:=

Out[82]=

Show the number of dimensions of the underlying manifold represented by the Christoffel symbols:

In[83]:=

Out[83]=

Show the signature of the underlying manifold represented by the Christoffel symbols (with +1s representing positive eigenvalues and -1s representing negative eigenvalues of the metric tensor):

In[84]:=

Out[84]=

Determine whether the underlying manifold represented by the Christoffel symbols is Riemannian (i.e. all eigenvalues of the metric tensor have the same sign):

In[85]:=

Out[85]=

Determine whether the underlying manifold represented by the Christoffel symbols is pseudo-Riemannian (i.e. all eigenvalues are non-zero, but not all have the same sign):

In[86]:=

Out[86]=

Determine whether the underlying manifold represented by the Christoffel symbols is Lorentzian (i.e. all eigenvalues of the metric tensor have the same sign, except for one eigenvalue which has the opposite sign):

In[87]:=

Out[87]=

Show the list of conditions on the coordinates required to guarantee that the underlying manifold represented by the Christoffel symbols is Riemannian (i.e. all eigenvalues of the metric tensor are positive):

In[88]:=

Out[88]=

Show the list of conditions on the coordinates required to guarantee that the underlying manifold represented by the Christoffel symbols is pseudo-Riemannian (i.e. all eigenvalues of the metric tensor are non-zero):

In[89]:=

Out[89]=

Show the list of conditions on the coordinates required to guarantee that the underlying manifold represented by the Christoffel symbols is Lorentzian (i.e. the "time" eigenvalue is negative, and all other eigenvalues are positive):

In[90]:=

Out[90]=

Show the list of coordinate values that cause the Christoffel symbols to become singular:

In[91]:=

Out[91]=

Compute the covariant form of the Christoffel symbols (with all indices lowered/covariant):

In[92]:=

Out[92]=

Compute the contravariant form of the Christoffel symbols (with all indices raised/contravariant):

In[93]:=

Out[93]=

Publisher

Jonathan Gorard

Version History

1.0.0 – 19 April 2023

Source Metadata

Citation:
- Charles W. Misner, Kip S. Thorne and John Archibald Wheeler (1973), Gravitation
- Stephen Wolfram (2002), A New Kind of Science
- Stephen Wolfram (2020), "A Class of Models with Potential to Represent Fundamental Physics"
- Jonathan Gorard (2020), "Some Relativistic and Gravitational Properties of the Wolfram Model"
- Jonathan Gorard (2020), "Some Quantum Mechanical Properties of the Wolfram Model"

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

ChristoffelSymbols

Details

Examples

Basic Examples (3)

Scope (3)

Publisher

Related Links

Version History

Source Metadata

Related Resources

License Information

ChristoffelSymbols

Details

Examples

Basic Examples (3)

Scope (3)

Publisher

Related Links

Version History

Source Metadata

Related Resources

Related Symbols

License Information