Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ChamferedPolyhedron

Source Notebook

Chamfer a given polyhedron

Contributed by: Jan Mangaldan

ResourceFunction["ChamferedPolyhedron"][poly]

gives the chamfered polyhedron of poly by chamfering all edges.

ResourceFunction["ChamferedPolyhedron"][poly,l]

chamfers the polyhedron poly by a length ratio l at its edges.

Details

Chamfering, or edge truncation, is done by truncating each edge of a polyhedron with the plane perpendicular to the plane bisecting the dihedral angle between two faces, effectively replacing each original edge with a hexagonal face.

Examples

Basic Examples (1) 

Chamfer a dodecahedron:

In[1]:=
ResourceFunction["ChamferedPolyhedron"][Dodecahedron[]]
Out[1]=
In[2]:=
Graphics3D[%]
Out[2]=

Scope (2) 

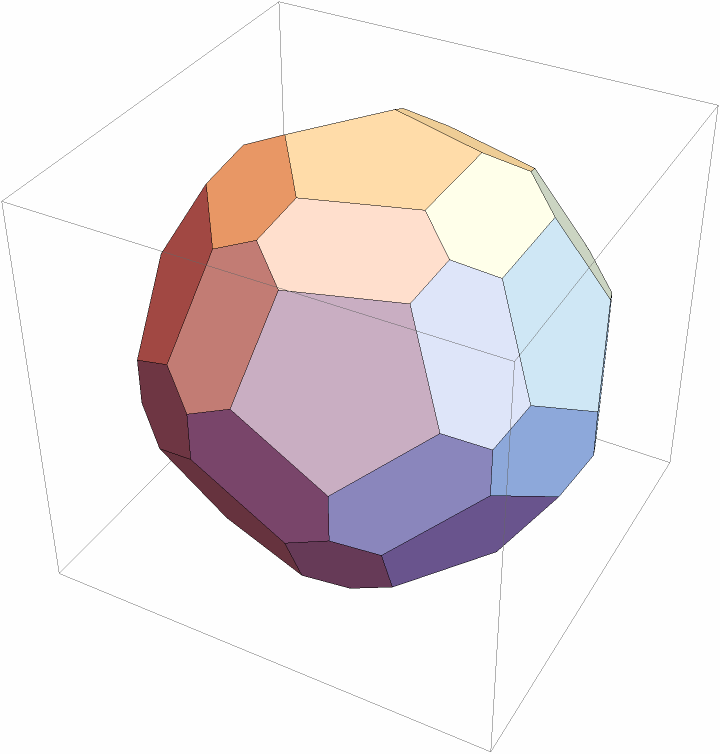ChamferedPolyhedron works on polyhedra:

In[3]:=
\[ScriptCapitalP] = PolyhedronData["TruncatedIcosahedron", "Polyhedron"];
In[4]:=
ResourceFunction["ChamferedPolyhedron"][\[ScriptCapitalP]]
Out[4]=
In[5]:=
Graphics3D[%]
Out[5]=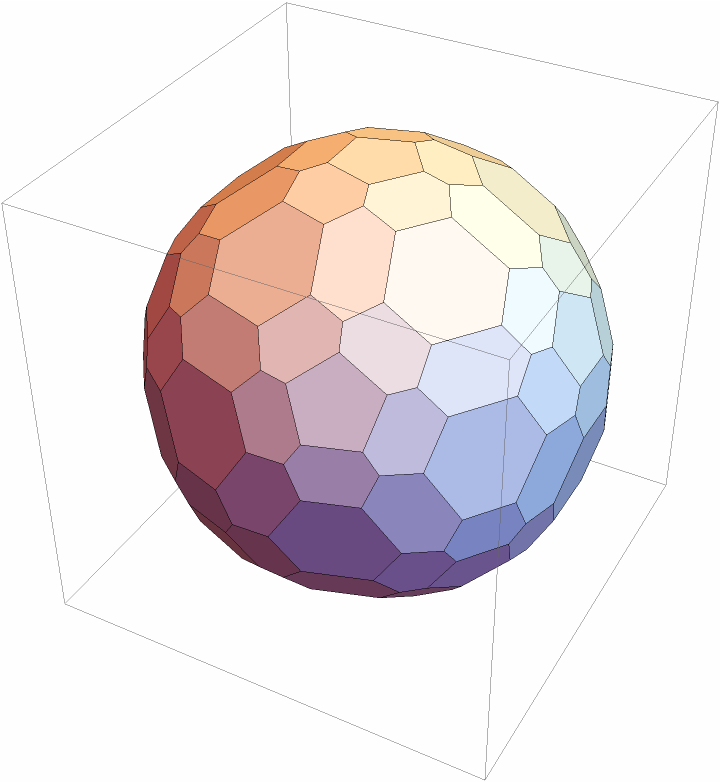

Chamfer the polyhedron by different length ratios:

In[6]:=
\[ScriptCapitalP] = PolyhedronData["DuerersSolid", "Polyhedron"];
In[7]:=
Table[Graphics3D[ ResourceFunction["ChamferedPolyhedron"][\[ScriptCapitalP], ratio]], {ratio, {0.3, 0.4, 0.5, 0.6}}]
Out[7]=

Properties and Relations (1) 

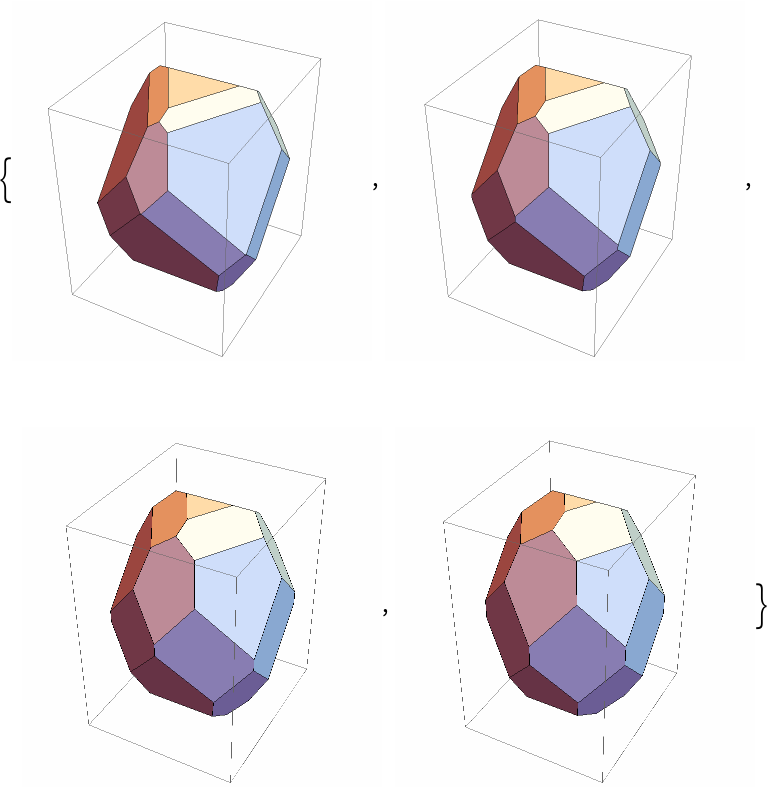ChamferedPolyhedron transforms edges, while BeveledPolyhedron transforms edges and vertices:

In[8]:=
With[{\[ScriptCapitalP] = Icosahedron[]}, GraphicsRow[{Graphics3D[\[ScriptCapitalP], PlotLabel -> "original"], Graphics3D[ ResourceFunction["ChamferedPolyhedron"][\[ScriptCapitalP]], PlotLabel -> "chamfered"], Graphics3D[BeveledPolyhedron[\[ScriptCapitalP]], PlotLabel -> "beveled"]}]]
Out[8]=

Possible Issues (1) 

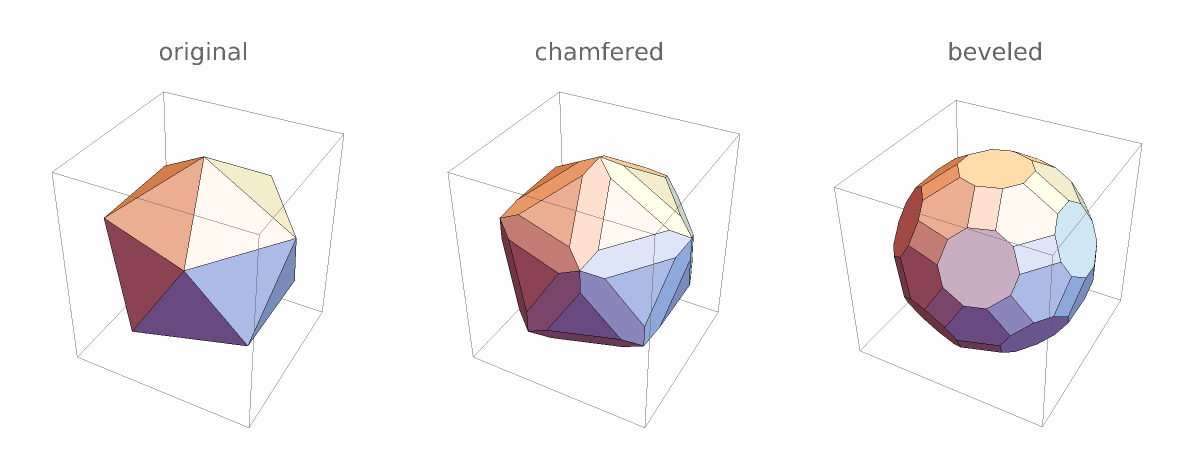ChamferedPolyhedron only supports simple polyhedra:

In[9]:=
\[ScriptCapitalP] = Polyhedron[{{0, 0, 0}, {1, 0, 0}, {0, 1, 0}, {0, 0, 1}, {1, 0, 0}, {2, 0, 0}, {1, 1, 0}, {1, 0, 1}}, {{1, 2, 3}, {1, 2, 4}, {2, 3, 4}, {1, 3, 4}, {5, 6, 7}, {5, 6, 8}, {6, 7, 8}, {5, 7, 8}}]
Out[9]=
In[10]:=
SimplePolyhedronQ[\[ScriptCapitalP]]
Out[10]=
In[11]:=
ResourceFunction["ChamferedPolyhedron"][\[ScriptCapitalP]]
Out[11]=

Neat Examples (2) 

Equilateral chamfered polyhedra based on Platonic solids:

In[12]:=
Grid[MapThread[{f, r} |-> {Graphics3D[f[1], Boxed -> False], \!\(\* GraphicsBox[ {GrayLevel[0.7], PolygonBox[{{0, 0}, {-0.5, 0.5}, {-0.5, 0.25}, {-1, 0.25}, {-1, -0.25}, {-0.5, -0.25}, {-0.5, -0.5}}]}, ImageSize->25]\), Graphics3D[ResourceFunction["ChamferedPolyhedron"][f[1], r], Boxed -> False]}, {{Tetrahedron, Cube, Octahedron, Dodecahedron, Icosahedron}, {(18 - 3 Sqrt[2])/17, (16 - 4 Sqrt[3])/13, ( 6 - Sqrt[6])/5, 2/41 (30 + 4 Sqrt[5] - Sqrt[365 + 158 Sqrt[5]]), 6/941 (186 + 12 Sqrt[5] - Sqrt[6145 + 2582 Sqrt[5]])}}]]
Out[12]=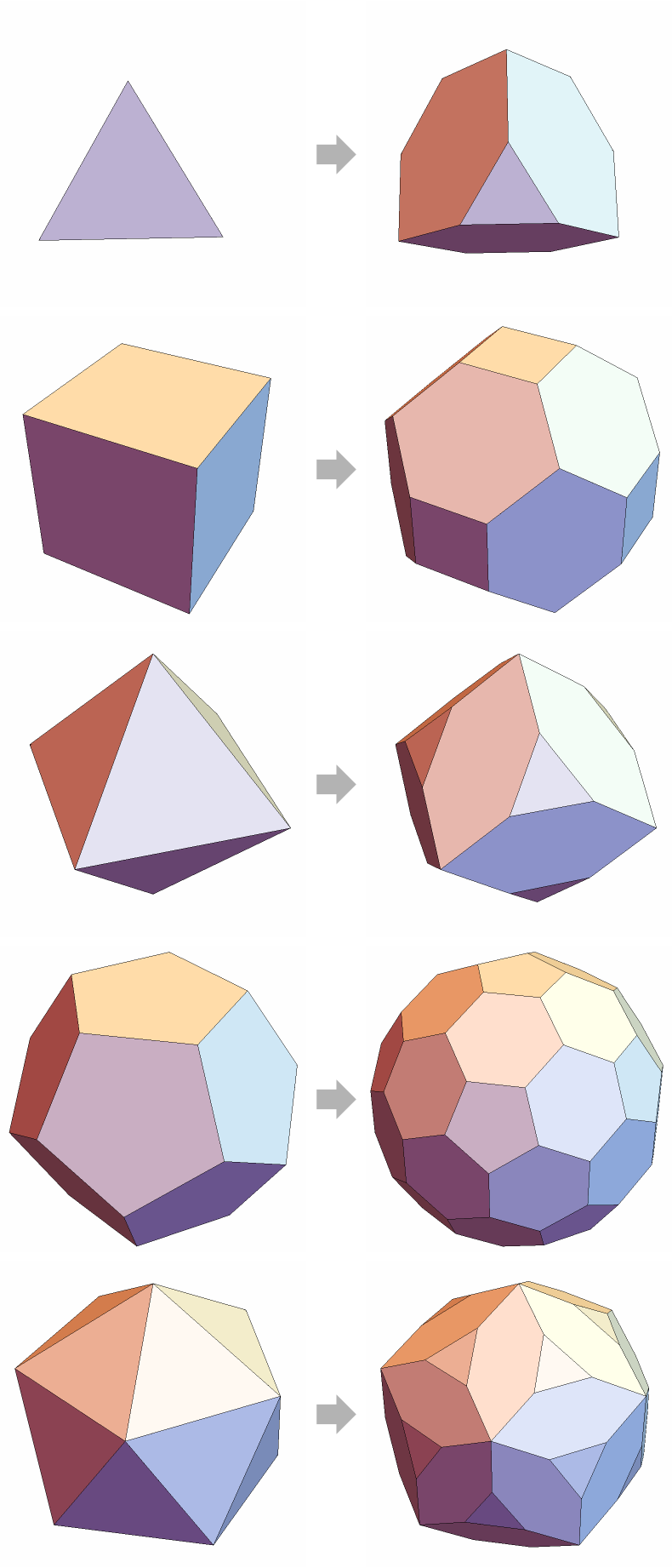

Show the relationship between a polyhedron and its chamfered version:

In[13]:=
Manipulate[ Graphics3D[{{Opacity[1/2], Dodecahedron[]}, ResourceFunction["ChamferedPolyhedron"][Dodecahedron[], r]}], {{r, 0.5}, 0.001, 0.999}]
Out[13]=

Version History

  • 1.0.0 – 21 September 2021

Related Resources

License Information