Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 Cevians

Source Notebook

Given a simplex and point, find the cevians

Contributed by: Ed Pegg Jr

ResourceFunction["Cevians"][simplex,point]

computes the cevians for a given simplex and point.

A cevian is a line segment joining the vertex of a triangle or tetrahedron to a point on the opposing edge or face.
The opposing edge or face is considered to be an infinite line or plane.
Given a 2D point, a 2D triangle has three cevians through that point.
Given a 3D point, a 3D tetrahedron has four cevians through that point.
Often, just the intersection points for a generated cevian are needed. ResourceFunction["Cevians"] returns these points in the same order as the given vertices.

Examples

Basic Examples (2) 

Find the generated cevians for a given triangle and point:

In[1]:=
tri = {{0, 0}, {4, 0}, {0, 3}}; pt = {1, 1/2}; cev = ResourceFunction["Cevians"][tri, pt]
Out[3]=

Show the cevians:

In[4]:=
Graphics[{EdgeForm[Black], LightGray, Triangle[tri], Black, Line /@ Transpose[{tri, cev}], Green, Disk[#, .1] & /@ cev, Red, Disk[pt, .1]}]
Out[4]=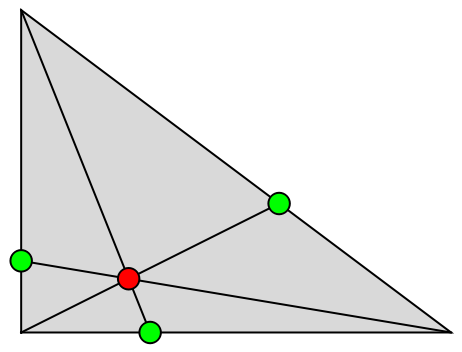

Verify Ceva's Theorem:

In[5]:=
pointtocevian = EuclideanDistance[pt, #] & /@ cev; vertextocevian = EuclideanDistance[#[[1]], #[[2]]] & /@ Transpose[{tri, cev}]; Total[pointtocevian/vertextocevian]
Out[7]=

Find the generated cevians for a given tetrahedron and point:

In[8]:=
tet = {{0, 0, 0}, {4, 0, 0}, {0, 3, 0}, {0, 0, 5}}; pt = {1, 1, 1}; cev = ResourceFunction["Cevians"][tet, pt]
Out[10]=

Show the cevians:

In[11]:=
Graphics3D[{EdgeForm[Black], {LightGray, Opacity[.5], Tetrahedron[tet]}, Line /@ Transpose[{tet, cev}], Green, Sphere[#, .1] & /@ cev, Red, Sphere[pt, .1]}]
Out[11]=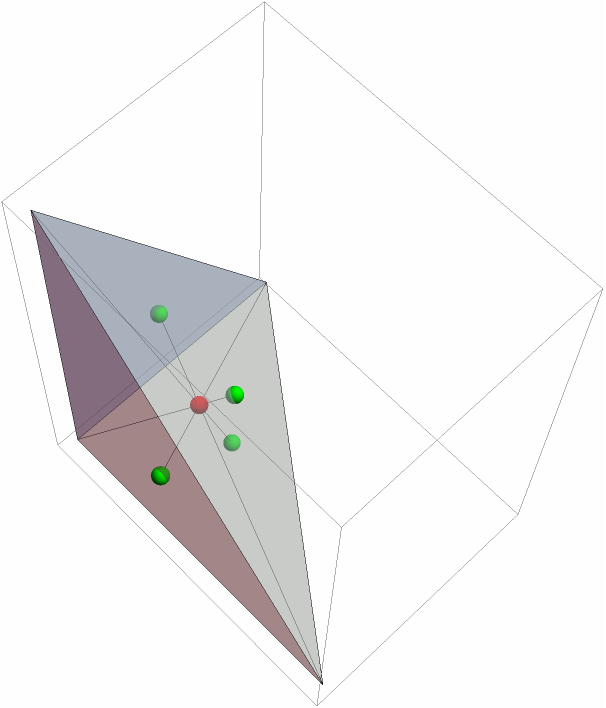

Verify Ceva's Theorem:

In[12]:=
pointtocevian = EuclideanDistance[pt, #] & /@ cev; vertextocevian = EuclideanDistance[#[[1]], #[[2]]] & /@ Transpose[{tet, cev}]; Total[pointtocevian/vertextocevian]
Out[14]=

Triangle and Point may be used:

In[15]:=
tri = {{0, 0}, {4, 0}, {0, 3}}; pt = {1, 1/2}; cev = ResourceFunction["Cevians"][Triangle[tri], Point[pt]]
Out[16]=

Tetrahedron and Point may be used:

In[17]:=
tet = {{0, 0, 0}, {4, 0, 0}, {0, 3, 0}, {0, 0, 5}}; pt = {1, 1, 1}; cev = ResourceFunction["Cevians"][Tetrahedron[tet], Point[pt]]
Out[18]=

Simplex and Point may be used:

In[19]:=
tri = {{0, 0}, {4, 0}, {0, 3}}; pt = {1, 1/2}; cev = ResourceFunction["Cevians"][Simplex[tri], Point[pt]]
Out[20]=

Symbolic variables may be used in a triangle:

In[21]:=
tri = {{0, 0}, {4, 0}, {0, 3}}; pt = {x, y}; cev = ResourceFunction["Cevians"][tri, pt]
Out[23]=

The cevians might not be on the line segments of the original triangle:

In[24]:=
tri = {{0, 0}, {4, 0}, {0, 3}}; pt = {7, 5}; cev = ResourceFunction["Cevians"][tri, pt]; Graphics[{EdgeForm[{Black, Thick}], LightGray, Triangle[tri], InfiniteLine /@ Subsets[tri, {2}], Gray, InfiniteLine /@ Transpose[{tri, cev}], Thick, Black, Line /@ Transpose[{tri, cev}], Green, Disk[#, .2] & /@ cev, Red, Disk[pt, .2]}]
Out[25]=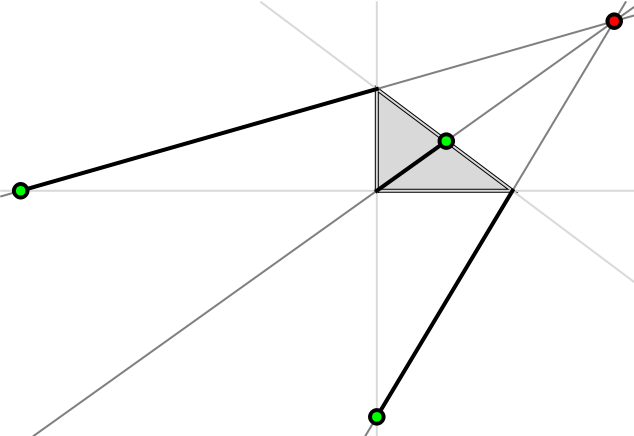

Symbolic variables currently do not work for a tetrahedron:

In[26]:=
tet = {{0, 0, 0}, {4, 0, 0}, {0, 3, 0}, {0, 0, 5}}; pt = {x, y, z}; cev = ResourceFunction["Cevians"][tet, pt]
Out[28]=

Calculate the Gergonne point and find the cevians:

In[29]:=
tri = {{1, 2}, {2, -1}, {-3, 0}}; ge = First@ResourceFunction["GergonnePoint"][tri]; cev = RootReduce[ResourceFunction["Cevians"][tri, ge]]
Out[31]=

Show the cevians and the incircle:

In[32]:=
Graphics[{EdgeForm[Black], LightGray, Triangle[tri], Black, Line /@ Transpose[{tri, cev}], Green, Disk[#, .1] & /@ cev, Red, Disk[ge, .1], Blue, Insphere[tri]}]
Out[32]=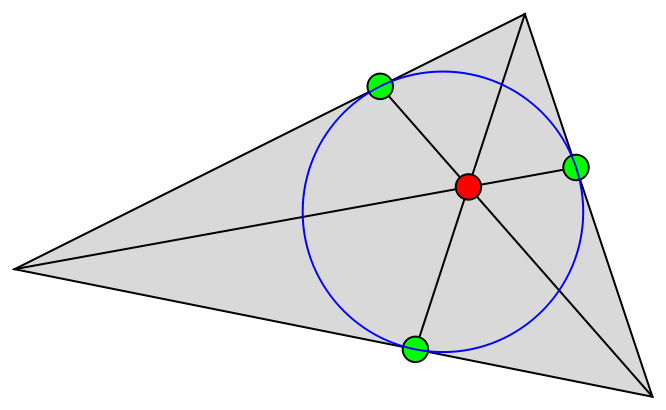

Compute some values for a tetrahedron:

In[33]:=
tet = {{0, 0, 0}, {14, 0, 0}, {145/28, Sqrt[17391]/28, 0}, {145/28, 35815/(28 Sqrt[17391]), 325 Sqrt[83/17391]}}; monge = RootReduce[ResourceFunction["Monge"][tet]][[1]]; cev = RootReduce[ResourceFunction["Cevians"][tet, monge]]; edgelengths = RootReduce[EuclideanDistance @@ # & /@ Subsets[tet, {2}]]
Out[34]=

Opposite edges of the tetrahedron have the same square sum, making it orthocentric:

In[35]:=
edgelengths^2 + Reverse[edgelengths^2]
Out[35]=

The cevians of the Monge point are the altitudes of the tetrahedron:

In[36]:=
Graphics3D[{Thick, {LightGray, Opacity[.2], InfinitePlane /@ Subsets[tet, {3}]}, Line /@ Transpose[{tet, cev}], Gray, Line /@ Subsets[tet, {2}], Green, Sphere[#, .2] & /@ cev, Blue, Sphere[#, .2] & /@ tet, Red, Sphere[monge, .2]}, SphericalRegion -> True, Boxed -> False]
Out[36]=

Requirements

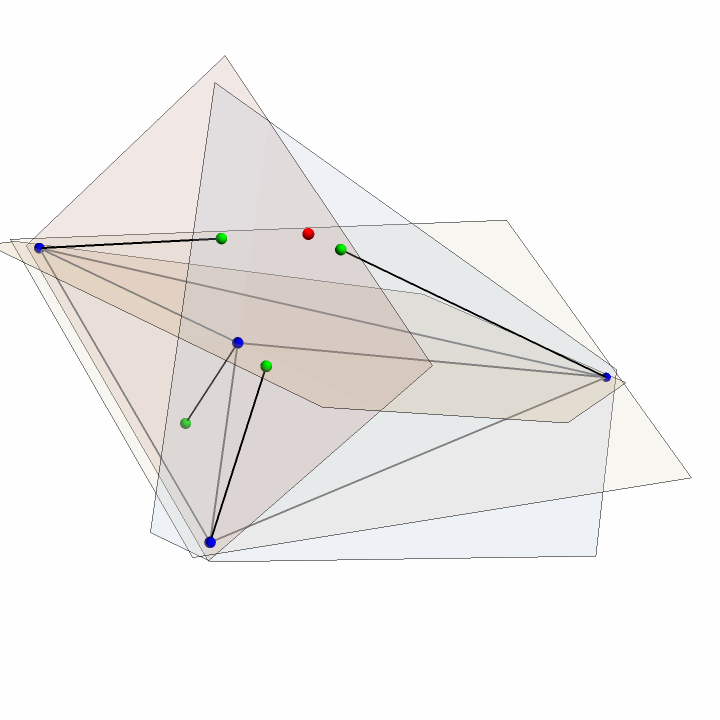Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.1.0 – 20 November 2023
  • 1.0.0 – 25 October 2023

Related Resources

License Information